3.1. Physical Modeling

During the years 1975-1982 were proposed several physical models of formation of grown-in microdefects: (i) equilibrium interstitial-type model [24]; (ii) non-equilibrium interstitial-type model [2]; local melting model (drop model) [37]; vacancy-type model [38]; vacancy-interstitial type model [23, 39]. In article [40] was carried out a critical review these of the physical models. The analysis showed that none of the models does not explain the experimental data on the research of grown-in microdefects. In 1982 he was proposed the recombination-diffusion model [20]. This model can be considered as a symbiosis of all pre-existing models.

Recombination-diffusion model assumes fast recombination of intrinsic point defects at the initial moment of cooling the grown crystal [20]. Fast recombination determines the type of dominant intrinsic point defects in the crystal. The result of the recombination selection depends on the ratio transport flows of intrinsic point defects in the growing crystal (determined the rate of crystal growth, V_g) and diffusion of intrinsic point defects near the crystallization front (determined by an axial temperature gradient, G). For large values of the ratio V_g/G the contribution of diffusion is assumed small. In this case will be dominated defects with higher initial concentration. For small values of V_g/G basic is expected contribution of diffusion. In this case will be dominated defects with higher diffusion coefficient.

In this model was first used mathematical tool which allows you to associate the defect structure of crystal with distribution in the crystal thermal fields during the growth. This was achieved by introducing into consideration the of the growth parameter V_g/G. It is assumed that in the case V_g/G < ξ_crit formed only interstitial A-microdefects as a result of aggregation of intrinsic interstitial silicon atoms. It is assumed that in the case V_g/G > ξ_crit formed only microvoids as a result of aggregation of vacancies. OSF-ring in this model represents a region where are of the small oxygen precipitates of vacancy type [9, 41].

In this physical model, the interaction between the impurities and intrinsic point defects is not considered [10]. It is assumed that at cooling of the crystals in the temperature range 1683...1423 K, depending on the thermal conditions of growth formed tiny (invisible) clusters of vacancies (D-microdefects) or intrinsic interstitial silicon atoms (B-microdefects). It is assumed that these clusters at 1223 K< T ≤ 1423 K transformed into a microvoids or interstitial dislocation loops (A-microdefects) accordingly [10]. This process of transformation leads to a sharp reduction in the concentrations of intrinsic point defects in the relevant parts of the crystal. With further cooling of the crystal residual intrinsic point defects are involved in the formation in these areas of oxygen clusters [9].

Recently within this model are made attempts to explain the effect of impurities on the formation of grown-in microdefects. In article [42] suggested that during the cooling of the crystal in the temperature range 1683...1423 K occurs the formation of complexes VO and VO₂ (where V is the vacancy, O is the oxygen). However, these complexes do not lead to the formation of precipitates in this temperature range. Free and bound (VO and VO₂) vacancies are expended initially on the formation of microvoids (1223 K< T ≤ 1423 K) and then are expended on the formation of O-clusters (precipitates of oxygen) at T < 1223 K [42]. Exactly the same approach applies to nitrogen impurity with similar results of calculations [43]. In the articles [42, 43] ignored the effect of impurities on the formation of interstitial grown-in microdefects. Also in these papers ignored the participation of intrinsic interstitial silicon atoms during the formation of vacancy microdefects.

In the general case recombination-diffusion model assumes that the process of defect formation in dislocation-free silicon single crystals occurs in four stages: (i) fast recombination of intrinsic point defects near the crystallization front; (ii) the formation in the narrow temperature range 1423...1223 K depending on the value of V_g/G microvoids or interstitial dislocation loops; (iii) the formation of oxygen clusters in the temperature range 1223...1023 K; (iv) growth of precipitates as a result of subsequent heat treatments.

Based on the synthesis of numerous experimental and theoretical research as the physical model we have developed the two-stage mechanism for the formation and transformation of grown-in microdefects ( or heterogeneous mechanism) [7, 14]. This physical model on the experimentally and theoretically established fact the absence of recombination of intrinsic point defects near the crystallization front of the crystal is based [44]. It is assumed that due to of the elastic interaction between the intrinsic point defects and the residual impurities the vacancies and intrinsic interstitial silicon atoms are drains on impurities of oxygen and carbon accordingly [14]. More details two-stage mechanism for the formation and transformation of grown-in microdefects will be discussed in paragraph 3.

3.2. Mathematical Modeling

At present, the defect formation processes in a semiconductor crystal, in general, and in silicon, in particular, have been described using the model of point defect dynamics; in this case, the crystal has been considered a dynamic system and real boundary conditions have been specified [10, 41-43, 45]. The mathematical model of point defect dynamics in silicon quantitatively explains the homogeneous mechanism of formation of microvoids and interstitial dislocation loops and provides the basis for the understanding of the relation between the defect crystal structure and the processes occurring in the melt [10]. The concentrations of defects have been calculated under the assumption of a rapid recombination of vacancies and intrinsic interstitial silicon atoms in a relatively narrow region in the vicinity of the crystallization front. This circumstance leads to the fact that primary defects (vacancies and intrinsic interstitial silicon atoms) are characterized by equilibrium concentrations [20]. The concentration of remaining primary defects after the passage of the narrow recombination region can be determined reasoning from the flux of defects deep into the crystal. Further cooling and pulling of the crystal are accompanied by the formation of aggregates of primary defects: microvoids in the region of dominance of vacancies and interstitial dislocation loops in the region of dominance of intrinsic interstitial silicon atoms.

In the general case, the model describing the defect dynamics in a crystal involves the kinetics of Frenkel reactions, nucleation of point defects, growth of clusters, and point defect balance [10]. The mutual annihilation and the formation of pairs of point defects over the entire volume of the crystal are considered in the kinetics of Frenkel reactions. A series of bimolecular reactions is considered in the section of nucleation of point defects. The motion of complexes of point defects in the direction from the melt-crystal interface is considered in the section of cluster growth. The balance of point defects includes their diffusion and convection, Frenkel reactions, and their consumption for the formation of clusters. The basic equations for the point defect balance are written in the following form:

Here, Ci,ν are the concentrations of vacancies (v) and intrinsic interstitial silicon atoms (i) in the crystal to be grown; Cie,νe and Di,v their equilibrium concentrations and diffusion coefficients, respectively; Jcl,j is the concentration of critical clusters; m* is the number of monomers; R_clis the radius of a critical cluster; Jξ,τ is the rate of cluster formation; k_1V is the recombination factor; τ is the time of cluster formation; ξ=z−∫τtVdτ' is the distance from the crystallization front to the region of cluster formation; and is the time between the instants of time t and τ.

In the simulation of the formation of interstitial dislocation loops and microvoids, the authors of the model of point defect dynamics consider their nucleation and formation in a narrow temperature range ξ=z−∫τtVdτ' at T > T_m- 300 K, where T_mis the melting temperature [10].

In Eqs. (1) and (2), the variations in the point defect concentrations are due to their diffusion (first term), convection (second term), Frenkel reactions (third term), their consumption for the existing clusters (fourth term), and the formation of new clusters (fifth term). The rate of consumption of point defects for the formation of new clusters is negligible and, subsequently, can be ignored [10].

The diffusion-limited growth rates of clusters (for any z and t) formed at the corresponding quantities ξ and τ are described by the equations

where ψ is the density of monomers in the cluster.

The equations for the nucleation rates are represented in the form

where F* is the maximum change in the free energy and ρ_site is the concentration of nucleation sites (in formula (5)).

The initial length or height of the crystal is taken to be 0. For the crystal with a finite length h, the equilibrium conditions are assumed to be dominant over the entire surface, including the crystal-melt interface:

The initial size of the steady-state critical cluster is negligible as compared to the microdefect size. Consequently, the initial size of the stable cluster insignificantly affects its final size. The initial size of the stable cluster (nucleus) is calculated from the number of monomers in the critical cluster:

Equations (1)-(13) together with the energy balance of the hot zone control and determine the quantitative dynamics of point defects. In semiconductor industry, the crystal quality has been frequently determined from the total concentration or total density and represented by the average size of existing clusters [10]. The total density of clusters is calculated by summation of clusters of different sizes in the current state:

The average cluster radius is defined as

where avg stands for the average volume.

The model of point defect dynamics under consideration is one-dimensional in nature, and, hence, the influence of the radial diffusion that is dominant in the vicinity of the surface of the crystal is disregarded. Therefore, the model can be applied to an axial distribution of defects in the crystal for fixed radial positions far from the surface. The energy balance can be calculated using the quasi-steady-state approximation [10].

It should be noted that, in the general case, the model of point defect dynamics includes three approximations: rigorous, simplified, and discrete-continuum approaches. The rigorous model requires the solution to integro-differential equations for point defect concentration fields, and the distribution of grown-in microdefects in this model is a function of the coordinates, the time, and the time of evolution of the size distribution of microdefects [41, 46]. A high consumption of time and cost for the performance of calculations required the development of a simplified model in which the average defect radius is approximated by the square root of the average defect area. This approximation is taken into account in the additional variable, which is proportional to the total area of the defect surface. The simplified model is effective for calculating the two-dimensional distribution of grown-in microdefects [42]. Both models use the classical nucleation theory and suggest the calculation of the formation of stable nuclei and the kinetics of diffusion-limited growth of defects. The discrete-continuum approximation suggests a complex approach: the solution to discrete equations for the smallest defects and the solution to the Fokker-Planck equation for large-sized defects [47].

4.1. Determination of Recombination Parameters of Point Defects

The inclusion of the entropy barrier and the coefficient of joint self-diffusion of vacancies and interstitial silicon atoms in thermodynamic calculations leads us to the conclusion that there exists a recombination barrier [7]. However, this conclusion is inconsistent with the Voronkov theory. It should be noted that the experimental results obtained from transmission electron microscopy and the heterogeneous mechanism of formation of grown-in microdefects confirm the theoretical assumptions made earlier by Hu [23] and Sirtl [39].

The microscopic model of a recombination barrier was thoroughly developed by Gösele et al., [48]. In essence, this model is as follows: the dependence of the barrier height on the temperature is determined by the configuration of intrinsic point defects at high temperatures. In the framework of the model under consideration, it is assumed that, at high temperatures, intrinsic interstitial silicon atoms and vacancies are extended over several atomic volumes (eleven atoms occupy ten unit cells). This means that, around a point defect, there is a disordered isotropic region extending up to the atoms involved in the second coordination sphere. According to the results reported in the aforementioned papers, recombination can occur only when defects of two types are simultaneously contracted in the vicinity of one atomic volume. Since the extended defect configurations are characterized by a larger number of microstates as compared to those of a point defect, this contraction leads to a decrease in the entropy and, consequently, an entropy barrier ∆S < 0 exists. As the temperature decreases, the entropy barrier is considerably reduced and disappears completely at low temperatures and defects readily recombine. This process is associated with the variations observed in the configurations of intrinsic point defects, which are extended at high temperatures and have a point dumbbell-like configuration at low temperatures, as was shown in [48]. It should be emphasized that the theory of extended defect configurations, as well as of a recombination barrier, was confirmed in a number of recent studies [49, 50].

At high temperatures the temperature dependence of the configurational entropy for the aforementioned model of a defect can be described by the relationship [51]:

where S_∞is the limiting value of the configurational entropy ScatT→Tm,Tm ,is the melting temperature, T_kand is the characteristic temperature. It was shown that

According to the model proposed in [48], the free energy of the recombination barrier can be represented by the formula ΔG=−TΔS, because the contribution of the enthalpy term ∆ H is negligible. The temperature dependence of the recombination barrier height is governed by the entropy of formation of point defects. Hence, we can write

Approximate estimation at a temperature T=T_m leads to the free energy of the recombination barrier ΔG1683K=2.014V [44].

The recombination time τ₁at high temperatures can be evaluated from the expression

where Ωis the volume of the crystal lattice in the model proposed by Gösele et al. [48] andr₀=3.10_-8 cm is the recombination radius. Approximate estimation at a temperature leads to the recombination time τ₀= 316 s. It should be noted that, according to the estimates made with the use of the recent data reported by Tang et al., [52] and Bracht et al., [53], we obtain τ₀= 110 and 132 s, respectively.

The recombination factor k_1v(T) is described by the theory of diffusion-limited reactions together with the kinetic activation barrier [41]. At high temperatures, the recombination factor can be written in the following form:

where c_s = 5·10²² cm^-3 is the atomic density. The estimation at a temperature T=T_m leads to the recombination factor k _IV (1683 K) = 6.3·10^-26 cm³/s. Lemke and Sudkamp [54] introduced the following criterion for “rapid recombination”: k _IV (1683 K)C_Vm≥ 20 s^-1, where C_Vm= 11.7·10¹⁴ cm^-3 is the vacancy concentration at . For our model of point defect dynamics, the criterion for rapid recombination does not hold.

Thus, we theoretically demonstrated that the process of recombination of intrinsic point defects in Fz-Si and Cz-Si single crystals in the vicinity of the crystallization front is hindered by the recombination barrier. Consequently, we can make the inference that vacancies and intrinsic interstitial silicon atoms find their sinks in the form of oxygen and carbon background impurities, respectively.

The recombination time τ₂ at low temperatures can be estimated from the relationship [55]

Under these conditions, Antoniadis and Moskowitz [56] evaluated the energy barrier at the temperature T = 1373 K (ΔG = ΔH = 1.4 eV) by means of comparing the experimentally measured lifetime of vacancies and the growth rate for a diffusion-limited reaction. The limiting value of the recombination time τ_∞= 634.13 s can be determined from relationship (23) at a temperature T=T_m. As a result, we obtain

Approximate estimation leads to τ₂ = 316.4 s at and τ₂ → 0 at T = 723 K (estimates without regard for the vibrational entropy). At low temperatures, the recombination factor k _IV ( T ) can be determined from the expression

where D1T=1.76⋅10−2exp−0.937/KTcm2 cm² s^-1 and DvT=1.70⋅10−3exp−0.457/kT cm² s^-1 [2]. Approximate estimation at a temperature T = 723 K leads to the recombination factor k _IV ≈ 10^-9 cm³ s^-1. Therefore, the criterion for rapid recombination is satisfied fairly well.

Consequently, the processes of recombination of intrinsic point defects at low temperatures (for example, under conditions of ion implantation) proceed at a rather high rate. Our theoretical calculations confirm the validity of the entropy barrier model, according to which the decrease in the barrier height is caused by the decrease in the configurational entropy with decreasing temperature.

The experimental data and the results obtained from thermodynamic calculations have demonstrated that the process of aggregation of point defects dominates over the process of recombination of intrinsic point defects. At high temperatures, the process of recombination makes an insignificant contribution to the process of aggregation. Consequently, vacancies and intrinsic interstitial atoms coexist in thermal equilibrium. As a result, intrinsic point defects of both types are simultaneously involved in the process of aggregation. The decomposition of a supersaturated solid solution of point defects occurs upon cooling through two mechanisms, namely, the vacancy and interstitial mechanisms, with the formation of oxygen-vacancy and carbon- interstitial agglomerates [14].

4.2. The Physical Classification and Physical Model of Formation and Transformation of Grown-in Microdefects

Absence of recombination intrinsic point defects at high temperatures allows us to propose a new physical model of the formation grown-in microdefects. We define it as a two-stage mechanism (or heterogeneous mechanism) of formation of grown-in microdefects. Both names of the physical model of formation of grown-in microdefects are equal. The first name describes the decomposition of the supersaturated solid solution of point defects during cooling through the vacancy and interstitial mechanisms. The second name describes the role of oxygen and carbon impurities in the formation of grown-in microdefects.

The basic concepts of the heterogeneous mechanism for the formation and transformation of grown-in microdefects imply the following [14]: (i) the recombination of intrinsic point defects at high temperatures can be neglected; (ii) background carbon and oxygen impurities are involved in the defect formation as nucleation centers; (iii) the decay of the supersaturated solid solution of point defects when the crystal is cooled from the crystallization temperature occurs in two independent ways (branches): vacancy and interstitial; (iv) the defect formation is based on primary agglomerates formed as the crystal is cooled from the crystallization temperature due to the interaction between the impurities and intrinsic point defects; (v) when the crystal is cooled at temperatures below 1423 K, depending on the thermal growth conditions, secondary grown-in microdefects are formed due to the interaction between intrinsic point defects; (vi) the secondary grown-in microdefects are formed due to the coagulation (microvoids and A-microdefects) and deformation (A-microdefects) effects; (vii) the vacancy and interstitial branches of the heterogeneous mechanism have a symmetry, which implies simultaneous processes of defect formation during the decay of supersaturated solid solution of point defects; and (viii) the consequence of this symmetry is the formation of vacancy and interstitial grown-in microdefects of the same type and, correspondingly, the growth of dislocation-free Si single crystals in the same vacancy-interstitial mode (Fig. 1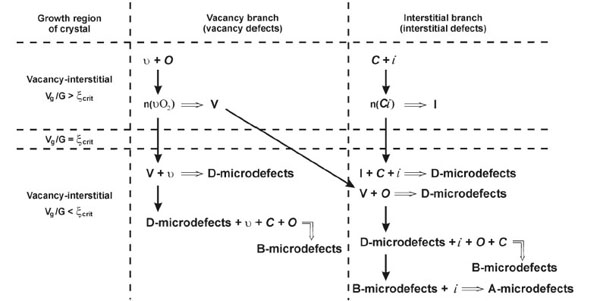). It was revealed that the growth parameter V_g/ G = ξ_crit describes the conditions under which the (111) face appears on the crystallization front [14].

Fig. (1) Schematic diagram of the heterogeneous formation of grown-in microdefects in dislocation-free Si single crystals: (I) agglomerates of the interstitial type, (V) agglomerates of the vacancy type, (C) carbon, (O) oxygen, (i) Si self-interstitials, and (v) vacancies.

The heterogeneous mechanism of the formation of grown-in microdefects assumes that the defect formation in dislocation-free Si single crystals upon cooling occurs in three stages: (i) the formation of impurity aggregates - primary grown-in microdefects near the crystallization front, (ii) the formation and growth of impurity precipitates upon cooling from the crystallization temperature, and (iii) the formation of microvoids or interstitial dislocation loops - secondary grown-in microdefects (depending on the growth parameter V_g/ G - in a narrow temperature range of 1423…1223 K [14].

The basic elements of defect formation are primary oxygen-vacancy and carbon-interstitial agglomerates, which are formed at impurity centers near the crystallization front. An excess concentration of intrinsic point defects (vacancies or silicon self-interstitials) arises when the crystal is cooled under certain thermal conditions. This process leads to the formation of secondary grown-in microdefects (А-microdefects or microvoids) (Fig. 2).

Fig. (2) Scheme of the physical classification of grown-in microdefects: (I) agglomerates of the interstitial type, (V) agglomerates of the vacancy type, (C) carbon, (O) oxygen, (i) Si self-interstitials, (v) vacancies.

The differences in the physical nature of the formation of primary and secondary grown-in microdefects allow one to consider the defect structure to be composed of two subsystems: primary and secondary grown-in microdefects (formed due to the impurity-intrinsic point-defect elastic interaction and the interaction between intrinsic point defects, respectively) [7, 14].

A detailed description of the heterogeneous mechanism formation of grown-in microdefects and its correspondence to the results of experimental researches are presented in the articles [7, 14].

4.3. The Diffusion Model for Formation of Grown-in Microdefects in Dislocation-Free Silicon Single Crystals

We propose a new diffusion model of the formation and transformation of grown-in microdefects. It is based on the experimental studies of undoped dislocation-free Si single crystals grown by the floating zone and Czochralski methods. The entire nomenclature of grown-in microdefects was investigated by transmission electron microscopy (TEM), standard patterns of grown-in microdefect macrodistribution depending on the thermal growth conditions were revealed, the transformation of grown-in microdefects during various technological treatments was analyzed, and the physical nature (sign of lattice strain) of all types of grown-in microdefects was determined [7, 14].

The diffusion model combines the physical model (the heterogeneous mechanism for the formation and transformation of grown-in microdefects), the physical classification of grown-in microdefects, and mathematical models of the formation of primary and secondary grown-in microdefects (Fig. 3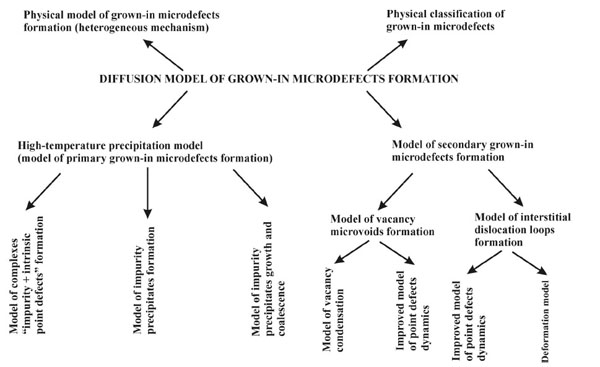). In paragraphs 4 and 5 we consider mathematical models for the diffusion model of the formation of grown-in microdefects.

Fig. (3) Diffusion model of grown-in microdefects formation.

5.1. Mathematical Model of Formation Complex “Impurity-Intrinsic Point Defect”

The solution is sought within the model of dissociative diffusion-migration of impurities [60]. In this case, the difference from the decomposition phenomenon is that during diffusion (as a technological process), a diffusant is supplied to the sample from an external source, whereas in the case of decomposition it is produced by an internal source (lattice sites). The theoretical analysis in the same; however, in deformation of dissociative diffusion, one has to take into account the surface concentration, which decreases in the sample volume with time and along the coordinate. The time constant is determined by the migration mechanism in the sample volume, while the coordinate dependence is determined by the sample shape and the boundary conditions of the diffusion problem.

It is difficult to interpret diffusion in multicomponent systems because it is necessary to take into account the interaction of impurity atoms. Generally, one has to use numerical methods to solve the equations; simple analytical expressions, convenient for comparison with the experimental data, can be obtained only in certain approximations. The mechanism of complex formation can be different; however, independent of the nature of the forces leading to the formation of complexes, any model assumes the action radius of these forces to be small. In this case, in analysis of the migration of point defects, a complex can be considered as a point defect.

Let us write the formation of complexes as a quasi-chemical reaction

Then, the thermodynamic equilibrium condition between the free impurities A and B and the impurity bound into AB complexes can be written in the form

where µ_A and µ_B are the chemical potentials of free impurities and µ_AB is the chemical potential of complexes.

If the total concentration of A and B impurities ( N_A,N_B) is low in comparison with the concentration of the main material, μAB=1nNAB in this approximation, and the equilibrium condition (27) can be written as

where Q is the concentration of complexes and k(T) is the constant of the complex formation reaction, which is temperature-dependent (at constant pressure) [61]. At k = 0, the impurity is totally bound into complexes (strong complex formation).

One should take into account that, in the diffusion equations written with allowance for the complex formation, the total impurity flux is the sum of the free impurity flux and the flux of the impurity bound into complexes [61]:

where , D_A,D_B andD_Q are the diffusion coefficients of the free components A and B and complexes, respectively; x is the coordinate (crystal length); and t is time.

The diffusion coefficient of complexes depends on the mechanism of complex formation and the type of their components. In particular, if a complex consists of two interacting atoms, the diffusion coefficient D_Qis much smaller than the corresponding diffusion coefficients of these atoms, D_Aand D_B . Therefore, assuming the complexes to be low-mobile, one can neglect the last terms in Eqs. (29) and (30):

Complexes are immobile; hence, the boundary conditions are written for the free impurity. Since the equilibrium settling time for the complexes and free impurity is much shorter than the characteristic diffusion time, the total impurity concentration can be set as the initial condition.

Vas’kin and Uskov [61] considered the problem of successive diffusion of a component A into a sample singly doped with a component B , taking into account the complex formation at the initial and boundary conditions:

In this case, the diffusion equation has the form

where λ=xDA⋅t2 is the Boltzmann substitution, primes denote differentiation with respect to λ and d2=DADB .

The solution to the system of equations (34) with the corresponding boundary conditions (diffusion of the impurity A from a constant source into a semiconductor that is homogeneously doped with the impurity B ; the impurity B does not evaporate) in the case of strong complex formation (k = 0) is [61]:

where

λ ₀is derived from the equation

Let us rewrite the system of equations (28)-(30) for the diffusion impurity kinetics of mobile complexes in terms of total components,N_A=H_A+Q and N_B=H_B+Q :

In Eqs. (35)-(41) and below, dA2=DA;dB2=DB;dQ2=DQ . In Eqs. (33)-(41) and below, H_Aand H_A are the concentrations of the free impurities A and B and N_AO and N _BO are the impurity concentrations at the interface.

Note that the solution to the system of equations is considered for the three cases that are most often met in practice: successive distribution, simultaneous diffusion, and interdiffusion. Under the conditions of our physical model, we can speak about successive diffusion, at which the condition of zero flux of one of the components (located at the initial instant in the sample bulk) is set at the interface. In this case, the boundary conditions have the form

Generally, the system of equations (39)-(41) with the boundary conditions (42) does not have an analytical solution; therefore, to analyze the shape of the impurity profiles, one has to analyze the limiting cases. Let us consider the approximation of strong complex formation (k = 0), which physically means that the A+B↔Q reaction is significantly shifted toward complex formation. In addition, at k = 0, it follows formally from the system of equations (39)-(41) that the concentration of at least one of the free components is zero; i.e.,H_A=0 or H_B=0 (the impurity is completely bound into complexes).

The solution to the problem of diffusion of a component A in a semi-infinite sample homogeneously doped with a component B , with the absence of evaporation of the component B from the sample and the presence of the free component A at the sample boundary, has the form [60]:

where S1x=exp−x2πxerfcx;S2x=exp−x2πxerfcx;NA0−NB1=HA0

Under physical-model conditions (heterogeneous mechanism of grown-in microdefect formation), we assume that the component A is the background impurity (oxygen O or carbon C ) and the component B is intrinsic point defects (vacancies V or interstitials I ). For the vacancy and interstitial mechanisms, we consider, respectively, the oxygen+vacancy ( O + V ) and carbon+interstitial ( C + I ) interactions.

The solution to Eqs. (37) and (38) has a physical meaning NB1∼1012...1014cm−3 only at λ≈0,01 . , ۃ₀ is interpreted as the front boundary of the complex formation reaction. The calculations performed in the framework of this approximation have demonstrated that the edge of the reaction front of the formation of a complex (i.e., the “oxygen+vacancy” and “carbon+interstitial silicon atom” complex) is located at a distance of ~3·10^-4 mm from the crystallization front [57]. Since x is the crystal length and is the position of the crystallization front, we can conclude that complex formation occurs near the crystallization front. Detailed calculations are presented in the articles [57, 58].

5.2. Mathematical Model for the Formation of Precipitates

Let us consider a system of a growing undoped dislocation-free silicon single crystal. The concentrations of all point defects at the crystallization front are assumed to be equilibrium, and both the vacancies and the intrinsic interstitial silicon atoms are present in comparable concentrations [62]. During cooling of the crystal after passing through the diffusion zone, an excessive (nonequilibrium) concentration of intrinsic point defects appears. Excess intrinsic point defects disappear on sinks whose role in this process is played by uncontrollable (background) impurities of oxygen and carbon [14]. In real silicon crystals, the concentrations of carbon and oxygen impurities are higher than the concentrations of the intrinsic point defects. The formation of complexes between the intrinsic point defects and impurities is governed, on the one hand, by the fact that both the intrinsic point defects and the impurities are sources of internal stresses in the lattice (elastic interaction) and, on the other hand, by the Coulomb interaction between them (provided the defects and the impurities are present in the charged state). The mathematical model under consideration allows for the elastic interaction and the absence of the recombination of intrinsic point defects in the high-temperature range [44]. The concentrations of intrinsic point defects Ci,vr,t in the growing crystal satisfy the diffusion ∂Ci,v∂t=Di,vΔCi,v−Cie,ve equation where r is the coordinate and t is the time. In the vicinity of the sinks (oxygen and carbon atoms), the concentration of intrinsic point defects C_ie,veis kept equilibrium, whereas the diffusion coefficients D_i,v and the concentrations C_ie,ve of intrinsic point defects decrease exponentially with decreasing temperature. Under these conditions, the formation of microvoids and interstitial dislocation loops is possible only at significant supersaturations of intrinsic point defects, which take place at a temperature T=T_m-300K (where T_m is the crystallization temperature) [10]. For the formation of precipitates in the high-temperature range T ~ 1683…1403 K has been calculated using the model of dissociative diffusion. This approximation is valid at the initial stages of the formation of nuclei, when their sizes are small and the use of Fokker-Planck continuity differential equations is impossible. The calculations performed in the framework of this approximation have demonstrated that the edge of the reaction front of the formation of a complex (i.e., the “oxygen+vacancy” and “carbon+interstitial silicon atom” complex) is located at a distance of ~3·10^-4 mm from the crystallization front [57]. This spacing represents a diffusion layer in which an excessive concentration of intrinsic point defects appears because the recombination of these defects at high temperatures is absent.

Now, we consider the modern approach based on solving systems of coupled discrete differential equations of quasi-chemical reactions for the description of the initial stages of the formation of nuclei of new phases and a similar system of Fokker-Planck continuity differential equations. The grown-in microdefects are treated as clusters of particles of different types, so that their formation and decay can be represented as a reaction involving random processes of attachment and detachment of particles X ,

where A_nis a cluster of the A type, which consist of n particles of the Xtype; g(n,r,t)is the growth rate of the A_n cluster and d(n,r,t)is the decay rate of the cluster. The concentration of the A_n clusters at the r point is determined by the function f(n,r,t) . The change of this function with time is described by the system of discrete kinetic differential equations

The conservation of the number of X particles is described by the equation

where n_maxis the maximum number of X particles contained in the Acluster.

By expanding the gradually n-dependent functions g,dand f into a Taylor series in terms to the second order included, the system of discrete equations is represented by the continuity partial differential equation (the Fokker-Planck equation) [63]

In this case, the flux of monomers in the space of n sizes is given by the formula

and the kinetic coefficients A and B are described by the expressions

When solving the system of equations (48) and (50), the fluxes J and I are joined at the point n=n_min . Then, the law of conservation of the number of particles (49) is transformed into the form

Equation (50) represents a diffusion drift equation that describes the evolution of the distribution function f in the space of n sizes. The system of equations (48)-(53) makes it possible within a unified model to consider the processes of nucleation and the subsequent growth of the clusters. The conventional boundary separating small and large clusters is considered to be n=n_min , which, in the calculations, is assumed to fall in the range from 10 to 20. This quantity represents the boundary between the range of sizes (n >_min ) in which the thermodynamic approach to the description of the physical processes can be considered valid and the range of sizes (n<_min) in which the atomic nature of these processes must be taken into account.

In order to describe the kinetics of the simultaneous nucleation and growth (dissolution) of a new phase particles of several types in a supersaturated solid solution of an impurity in silicon, it is necessary to consider a system consisting of oxygen and carbon atoms, vacancies, and intrinsic interstitial silicon atoms. The interaction in this system during cooling of the crystal from 1683 K results in the formation of oxygen and carbon precipitates [14]. In order to perform the computational experiments and to interpret their results, it is necessary to carry out a dimensional analysis of the kinetic equations and the conservation laws with the use of characteristic time constants and critical sizes of defects. This will make it possible to perform a comparative analysis of the joint evolution of oxygen and carbon precipitates and to optimize the computational algorithm for the numerical solution of the equations.

The nucleation and evolution of a complex system of grown-in microdefects (which consists of oxygen and carbon precipitates) during cooling of the crystal are described by the systems of coupled differential equations (48)-(53) for each type of defect. These systems are related by the laws of conservation of point defects, which determine the current values of their concentrations in the crystal and affect the rates of growth and dissolution of clusters of all types. For the case of a thin plane-parallel crystal plate of a large diameter, when the conditions in the plane parallel to the surface of the crystal can be considered to be uniform and the diffusion can be treated only along the normal to the surface (the z coordinate axis), the mass balance of point defects in the crystal is described by the system of diffusion equations for intrinsic interstitial silicon atoms, oxygen atoms, carbon atoms, and vacancies:

In the system of equations (54), we took into account that the oxygen precipitates serves as sinks for oxygen atoms and vacancies and as sources of interstitial silicon atoms. Then, we can write the following equations:

At the same time, the carbon precipitates, in turn, also serve as sinks for carbon atoms and interstitial silicon atoms and as sources for vacancies. Therefore, we can write

In the general case, the proportionality factors γv,γi,γv∗,γi∗ can depend on the quantities n_o,n_c and are determined by the conditions of thermodynamic equilibrium [64]. Moreover, in the system of equations (54), the recombination of pairs of intrinsic interstitial silicon atoms and vacancies is ignored [14].

The corresponding system of coupled Fokker-Planck equations can be transformed into the dimensionless form

where τ=tt0 is the dimensionless time. The time constants in the system of equations (57) are given by the expressions t0=n0cr,0 2/gSiO20;tc=nccr,02/gSiC0, , where the critical growth rates of the precipitates are defined as . gSiO20=NO0νOexp−GactSiO2/kT;gSiC0=NO0νcexp−GactSiC/kT The normalized sizes of the precipitates are determined in the system of equations (57) as follows: ν˜o=n0/nocr,0;ν˜c=nc/nccr,0 , where nocr,nccr are the normalizing critical sizes of the precipitates. The quantities NO0=4πrocr,02δSio2COeq;Nc0=4πrccr,02δSiCCceq are the numbers of particles in the vicinity of the corresponding precipitates with critical sizes. The size distribution functions of the precipitates in the system of equations (57) are normalized to the initial concentrations of the corresponding nucleation centers:

The fluxes of particles on the right-hand sides of the system of equations (57) are described by the expressions

in which the following notation is used for the normalized kinetic coefficients:

The normalized rates of growth and dissolution of the precipitates in expressions (60) and (61) take the form

The critical size of the precipitates can be determined according to [64, 65] from the expressions

where So=CoCoeg,Sc=CcCceg,Si=CiCiegSv=CvCveg are the supersaturations of the oxygen atoms, carbon atoms, intrinsic interstitial silicon atoms, and vacancies, respectively; σ is the density of the surface energy of the interface between the precipitate and the matrix µ is the shear modulus of silicon δ and e are the relative linear and volume misfit strains of the precipitate and the matrix, respectively g_i and g_v are the fractions of the intrinsic interstitial silicon atoms and vacancies per impurity atom attached to the precipitate, respectively; is the molecular volume of the precipitate; and u=1+γix+γν−1⋅1+ϵ1+δ3 .

The number of impurity atoms in the compressed precipitates with the radii and is determined according to [65] from the formula

where is the volume of the precipitate; is the fraction of impurity atoms per intrinsic defect, ≤ 2, ≤ ½, ≤ ½.

When analyzing the evolution of precipitates during cooling of the crystal in the course of its growth, the important parameters are the characteristic constants in the size space: the critical sizes of the corresponding precipitates and the related characteristic time constants, which specify the scale of changes in the size distribution function of microdefects with time. The time constants in the system of equations (57) allow one to calculate the normalizing sizes nOcr,0 and nCcr,0 ; for this purpose, the supersaturations corresponding to the complete inclusion of the oxygen and carbon atoms in the precipitates are substituted into expressions (63) and (64). In each of these expressions, the supersaturations of the remaining point defects are assumed to be equal to unity.

An increase in the supersaturations of point defects (oxygen and carbon atoms, intrinsic interstitial silicon atoms, and vacancies) leads to a decrease in the corresponding critical size of the precipitates and favors an acceleration of their growth. A decrease in the characteristic times also leads to an acceleration of the precipitation with an increase in the supersaturations of the point defects. The opposite trend is observed when the crystal is cooled from the crystallization temperature.

An important property of the characteristic times is their inverse proportionality to the products of the characteristics of point defects (diffusion coefficients and equilibrium concentrations):

Since the product of the characteristics of point defects for oxygen atoms considerably exceeds the analogous product for carbon atoms, the rate of evolution of the size distribution function of the carbon precipitates should exceed the corresponding rate for oxygen precipitates. This means that the evolution of the microdefect structure of dislocation-free silicon single crystal during cooling of the as-grown crystal is determined predominantly by the growth rate of the oxygen precipitates. Detailed quantitative information on the characteristics of the primary grown-in microdefects can be obtained by numerically calculating the system of equations (57).

The algorithm used for solving the problem of simulation of the simultaneous growth and dissolution of the oxygen and carbon precipitates due to the interaction of point defects during cooling of the crystal from the crystallization temperature is based on the monotonic explicit difference scheme of the first-order accuracy as applied to the Fokker-Planck equations (57). Detailed calculations are presented in the articles [59].

These calculations demonstrate that intrinsic point defects (vacancies and intrinsic interstitial silicon atoms) exert a significant influence on the dynamics of mass exchange and mass transfer of point defects between the oxygen and carbon precipitates. The absorption of vacancies by the growing oxygen precipitates leads to the emission of silicon atoms into interstitial positions. The intrinsic interstitial silicon atoms, in turn, interact with the growing carbon precipitates, which, in the process of growth, supply vacancies for growing oxygen precipitates. This interaction leads to such a situation that, first, the growth of the precipitates is suppressed more weakly because of the slower increase in the supersaturation of the intrinsic point defects in the bulk of the growing crystal and, second, the critical radius of the formation of carbon precipitates increases more slowly, which favors a more rapid growth of the carbon precipitates.

09-Headinigher rate of the evolution of the size distribution function for carbon precipitates can be associated with the higher mobility of interstitial silicon atoms as compared to vacancies in the high-temperature range. It can be assumed that the mutual formation and growth of oxygen and carbon precipitates result in a lower rate of the evolution of the size distribution function of the oxygen precipitates, regardless of their smaller critical size at the initial instant of time, owing to the effect of the carbon impurity.

The results of approximate calculations of the Fokker-Planck partial differential equations correlate well with the results of the analytical solution of the equations in the consistent model of dissociative diffusion in the approximation of strong complex formation [60]. The main advantage of these two models is that they complement each other. In particular, the critical size distribution functions of the oxygen and carbon precipitates can be found only from the Fokker-Planck continuity differential equations, whereas the consistent model of dissociative diffusion in the approximation of strong complex formation has failed to obtain these functions. At the same time, the model of dissociative diffusion makes it possible to analyze the processes occurring in the diffusion region near the crystallization front. Of special note is the fact that these mathematical models, together with the experimental results obtained from the investigation of quenched crystals, have demonstrated that the nucleation processes occur very rapidly near the crystallization front.

5.3. Model of Growth and Coalescence of Precipitates

In the classical theory of nucleation and growth of new-phase particles, the process of precipitation in a crystal is treated as a first-order phase transition and the kinetics of this process is divided into three stages: the formation of new-phase nuclei, the growth of clusters, and the coalescence stage.

At the second stage of the precipitation process, clusters grow without a change in their number. This growth is accompanied by a considerable decrease in the degree of supersaturation of the solid solution. It is assumed that the growth kinetics of precipitates is described by the reversible scheme A_iC+A « A_i+1C , which corresponds to the growth of precipitates at the nucleation centers C with a concentration N_c that remains unchanged with time. The nucleation centers attach and detach monomers, which is described by the system of equations [66]:

where N_i is the volume-average concentration of nucleation centers that attach i particles, N is the monomer concentration, k_iN is the rate of attachment of a monomer for a nucleation center, and is the rate of detachment of a monomer for a nucleation center. At the initial instant of time, the system contains only monomers and nucleation centers. The growth of precipitates is limited by the monomer diffusion. The kinetic coefficients are given by the formula k_i4 π R_iD, where is the radius of attachment of a free particle by a cluster consisting of i particles and D is the diffusion coefficient of a free particle.

The system of equations (67) obeys the law of conservation of nucleation centers Nc=∑i=1Nit and the law of conservation of the total number of particles, including both monomers and particles involved in precipitates, i.e., N0=Nt+∑i=1iNi , where N(O) is the monomer concentration at the initial instant of time. Therefore, the average number of particles at the nucleation centers can be represented in the form

For i >> 1 the process is described using the Fokker-Planck equation. In accordance with the principle of detailed balance gi=ki−1NECEi−1/CEi≈kiNE , the Fokker-Planck equation takes the form [66]:

where N_E is the equilibrium concentration of monomers.

In the case of the diffusion-controlled precipitation, the mathematical expectation i(t) can be described by the macroscopic equation corresponding to expression (69) :

where k₀4πR_iD, m is the initial size of precipitates, and is the parameter dependent on the cluster geometry.

Expressions (68) and (70) allow us to write the differential equation that describes the variation in the monomer concentration during the decomposition of the solid solution:

The kinetics of decrease in the monomer concentration, which is determined from the numerical solutions to the system of initial equations (67), coincides with that obtained from expression (71), to within the error of numerical methods. The solution of the system of initial equations (67) for real objects is nearly impossible due to the large dimension of the system of equations, whereas the solution of Eq. (71) presents no special problems [66].

The kinetics of decrease in the monomer concentration as a result of the decomposition of the solid solution at m=0 can be written in the form

By numerically solving Eq. (71) simultaneously with Eq. (68), we can calculated the average radius of the precipitate at the growth stage:

At the third stage of the precipitation process, when the particles of the new phase are sufficiently large, the supersaturation is relatively low, new particles are not formed and the decisive role is played by the coalescence, which is accompanied by the dissolution of small-sized particles and the growth of large-sized particles. The condition providing for changeover to the coalescence stage is the ratio ut=RtRcrt≈1 , where R_cr(t) is the critical radius of the precipitate. Under this condition, the precipitate is in equilibrium with the solution dRdt=0

The precipitate grows at R(t)>R_cr(t) and dissolves at R(t)< R_cr(t). With time, the critical radius R_cr(t) increases and the number of particles per unit volume decreases [66]. The solution of the system of equations describing this process is possible only in the case where the supersaturation of the solute tends to zero.

Slezov and Kukushkin [67] showed that the crystallization of single-component melts is accompanied by the formation of temperature fields and that the precipitates of the new phase interact with each other through generalized temperature fields. The asymptotic solution to the system of equations describing this process is similar to the solution of the equations describing the diffusion isothermal coalescence [67] and becomes possible when the supercooling of the melt ΔT=T_c0 tends to zero (where T_c and T₀ are the average and equilibrium temperatures of the crystal, respectively [67]).

Let us consider a solid solution that contains single-component spherical precipitates of a new phase with the initial size distribution function . The system containing the solid solution is thermally insulated and does not involve sources of a substance. Let the initial temperature and the initial concentration of the solid solution be T_c(0) andC_c(0) , respectively. The solution is considered at the coalescence stage.

Since the system in which the solid solution decomposes is thermally insulated, the heat of the phase transition that releases in the course of the coalescence leads to an increase in the temperature of the entire system, which, in turn, leads to a change in the equilibrium concentration c [67]. In this case, the supersaturation will tend to zero more rapidly than in the case of isothermal coalescence, because the increase in the temperature results in an increase in the equilibrium concentration. This will lead to a decrease in the concentration gradient between the solution and the precipitation of the new phase, and, correspondingly, the growth rate of precipitates decreases. Consequently, the diffusion and thermal fields become self-consistent and the system of equations of the nonisothermal coalescence should involve both the mass balance equation and the heat balance equation. The system of equations describing the nonisothermal coalescence has the form [67]

where expression (74) is the equation of continuity in the space of sizes for the size distribution function of precipitates, expression (75) is the mass balance equation, expression (76) is the equation accounting for the amount of released heat, f₀(R) is the initial size distribution function of precipitates, T₀ is the initial temperature of the solid solution, x=4π/3ν is the volume per atom in the precipitates of the new phase, Q(T_(c)) is the total amount of the material in the precipitates and the solution,c_c(t) is the solute concentration in the solid solution,L is the heat of the phase transition per atom of the precipitated phase, c_p is the heat capacity at constant pressure per unit mass of the solid solution, and p_t is the density of the solid solution. The average temperature of the solid solution is a function of the amount of the material in the precipitates of the new phase; i.e., Eqs. (9) and (10) are related to each other.

In order for the system of equations (74)-(76) to be complete, it is necessary to find the dependence of the growth rate of precipitates dR/dt on the radiusR :

Here, D is the diffusion coefficient for the component forming the new phase ∂c∂r is the concentration gradient of atoms at the precipitate boundary, which will be determined from the quasi-steady-state (the supersaturation is relatively low) solution of the diffusion equation written in the spherical coordinates

with the boundary conditions [67]

where β is the specific boundary flux, which includes the rate of incorporation of the emission of atoms into the precipitate; C_R is the concentration of atoms in equilibrium with the precipitate of radius R and c(R) is the concentration at the surface of the precipitate of the new phase. In the case of nonisothermal coalescence, the concentrations C_c,c(R),C_R are functions of the temperature T_c . The equation for the growth rate of a precipitate is obtained by solving Eq. (12) with the boundary conditions (79):

where is the equilibrium concentration of the solute at the temperature and is the surface tension at the interface between the precipitate of the new phase and the solid solution. It follows from expression (80) that there are two possible processes limiting the growth rate of the precipitate [67].

(1) The diffusion processes for D<<β:nR

(2) The processes occurring at the precipitate boundary for : D>>βnR;:

Equations (74)-(76) with either expression (81) or expression (82) form the complete system of equations that describe the process of nonisothermal decomposition of the solid solution at the stage of the coalescence. Slezov and Kukushkin [67] showed that, in closed systems in the absence of sources (sinks) of heat and matter, the dependences of the variations in the distribution functions for precipitates of the new phase over the sizes, their density, and the critical and average radii in the case of nonisothermal coalescence are identical to those observed in the case of isothermal coalescence. Only the constants dependent on the temperature are changed. Equations (74)-(76), together with either expression (81) or expression (82), are solved using the method developed in [67]. In the general case, the size distribution function for precipitates has the following form:

The average size of precipitates at the stage of the coalescence is proportional to the cube root of time [67]:

where D(t) is the diffusion coefficient of impurity atoms, β=σΩkTN0;Rcrt0 ; is the initial critical radius, σ is the surface tension at the precipitate-solid solution interface, W is the atomic volume, and

Here,t₀ is the initial critical time and N_c is the initial concentration of precipitates.

Detailed calculations are presented in the articles [66]. The analysis was carried out under the assumption that precipitates grow at a fixed number of nucleation centers according to the diffusion mechanism of growth. The model corresponds to the precipitation uniform in the volume. An analysis of the results obtained and the data taken from [57, 59] has demonstrated that the phase transition occurs according to the mechanism of nucleation and growth of a new phase so that these two processes are not separated in time and proceed in parallel.

The condition providing changeover to the stage of the coalescence is written in the form R(t)≈R_cr(t), which is satisfied for large-sized crystals at the temperature T ≈ 1423 K. Taking into account the computational errors, this temperature for large-sized crystals corresponds to the initial point of the range of the formation of microvoids (at V_g = 0.6 mm/min). In this range, all impurities are bound and there arises a supersaturation with respect to vacancies, which is removed as a result of the formation of microvoids. With a change in the thermal conditions of the growth (for example, at V_g = 0.3 mm/min [10]), there arises a supersaturation with respect to interstitial silicon atoms, which leads to the formation of interstitial dislocation loops. In this case, the condition R(t)≈R_cr(t) is satisfied at T ≈ 1418 K. Consequently, the stage of the coalescence in large-sized silicon single crystals begins at temperatures close to the temperatures of the formation of clusters of intrinsic point defects (depending on the thermal growth conditions, these are microvoids or interstitial dislocation loops).

The simultaneous nucleation and growth of particles of the new phase (oxygen and carbon precipitates) during cooling of as-grown silicon crystals leads to a strong interplay between the processes of evolution of these two subsystems of grown-in microdefects. The absorption of vacancies by growing oxygen precipitates results in the emission of silicon atoms in interstitial sites. In turn, the intrinsic interstitial silicon atoms interact with growing carbon precipitates, which, in the course of their growth, supply vacancies for growing oxygen precipitates. This interplay between the processes leads to an accelerated changeover of the subsystems of oxygen and carbon precipitates to the stage of the coalescence as compared to the independent evolution of these two subsystems.

The change in the thermal conditions for the growth of small-sized FZ-Si single crystals (high growth rates and axial temperature gradients) leads to the fact that the stage of the coalescence begins far in advance (at T ≈T_m-20K). The results of theoretical calculations have demonstrated that a decrease in the concentrations of oxygen and carbon in small-sized single crystals leads to a further decrease in the time of occurrence of the growth stage of precipitates. The change in thermal conditions of crystal growth (in particular, an increase in the growth rate and in the axial temperature gradient in the crystal) substantially affects the stage of the growth of precipitates. In turn, the decrease in the time of occurrence of the growth stage of precipitates is associated, to a lesser extent, with the decrease in the concentration of impurities in crystals. Eventually, these factors are responsible for the decrease in the average size of the precipitates.

Kinetic model of decomposition of solid solutions of oxygen and carbon impurities not only allows one to simulate the processes of precipitation during cooling of the as-grown silicon crystal to a temperature of 300 K but also adequately describes the available experimental data on the oxygen and carbon precipitation. The kinetic model of growth and coalescence of oxygen and carbon precipitates in combination with the kinetic models describing their formation [57, 59] represents a unified model of the process of precipitation in dislocation-free silicon single crystals. In the future, the mathematical apparatus of this model will make it possible to take into account and analyze interactions of intrinsic point defects not only with oxygen and carbon background impurities but also with other impurities (for example, transition metals, nitrogen, hydrogen, etc.), as well as interactions of the impurity-impurity type.

6.1 Kinetics of Formation of Microvoids

The experimentally determined temperature range of the formation of microvoids in crystals with a large diameter is 1403…1343 K [34]. In this respect, the approximate calculations for the solution in terms of the model of point defect dynamics were performed at temperatures in the range 1403…1073 K. The computational model uses the classical theory of nucleation and formation of stable clusters and, in strict sense, represents the size distribution of clusters (microvoids) reasoning from the time process of their formation and previous history.

The system of equations is solved using the exact space-time discretization. The algorithm involves the solution to the equation Vg=dhdt for the crystal growth rate with the simultaneous solution to Eqs. (1)-(4) with the boundary and initial conditions (7)-(11). The size distribution is determined from the solution to Eqs. (3) and (4) for the corresponding type of grown-in microdefects (microvoids or A-microdefects). The recombination factor in the calculation was taken to be k_1V=0 [44].

In the high-temperature range (1682 K <T <1403 K, the growth parameter is V_g/G >_crit), there occur nucleation and growth of impurity precipitates [14]. In this range, the supersaturation of intrinsic point defects (vacancies) is low and, hence, the nucleation rate of microvoids is negligible. At T≤ 1403 K, the supersaturation increases, which leads to an increase in the nucleation rate of microvoids. After the formation of microvoids, their growth is accompanied by a rapid consumption of vacancies. As a result, the supersaturation decreases and the nucleation rate of microvoids decreases drastically. The nucleation dominates in a narrow temperature range, and, therefore, the nucleation of microvoids outside the zone of their formation is ignored. Moreover, since the growth rate of microvoids decreases sharply with an increase in their size and the corresponding decrease in the vacancy concentration, the growth of microvoids outside the nucleation zone is also disregarded.

The calculations were carried out in the framework of the model of point defect dynamics, i.e., for the same crystals with the same parameters as in already the classical work on the simulation of microvoids and interstitial dislocation loops (A-microdefects) [10]. According to the analysis of the modern temperature fields used when growing crystals by the Czochralski method, the temperature gradient was taken to be G = 2.5 K/mm [10]. The simulation was performed for crystals 150 mm in diameter, which were grown at the rates V_g= 0.6 and 0.7 mm/min. These growth conditions correspond to the growth parameter V_g/ G > ξ_crit.

Detailed calculations are presented in the articles [68]. Our results somewhat differ from those obtained in [10]. These differences are as follows: (i) the nucleation rate of microvoids at the initial stage of their formation is low and weakly increases with a decrease in the temperature and (ii) a sharp increase in the nucleation rate, which determines the nucleation temperature, occurs at a temperature T~ 1333 K. These differences result from the fact that the recombination factor in our calculations was taken to be k_1V=0 . For k_1V≠0 , consideration of the interaction between impurities and intrinsic point defects in the high-temperature range becomes impossible, which is accepted by the authors of the model of point defect dynamics [10]. In this case, in terms of the model, there arises a contradiction between the calculations using the mathematical model and the real physical system, which manifests itself in the ignoring of the precipitation process [10].

An increase in the crystal growth rate only insignificantly decreases the critical pore radius and weakly affects the nucleation temperature. As is known, in order to prevent the formation of microvoids, the cooling rate should be increased above 40 K/min [69]. These conditions are fulfilled when growing small-sized silicon crystals. For real growth rates of large-sized single crystals (with a diameter of larger than 80 mm), the formation of microvoids cannot be suppressed [70].

6.2. Kinetics of Formation of Interstitial Dislocation Loops (A-Microdefects)

The computational experiment was performed similarly to the calculations of the formation of microvoids. The simulation was performed for crystals 150 mm in diameter, which were grown at the rates V_g= 0.10 and 0.25 mm/min for the temperature gradient G = 2.5 K/mm. These growth conditions correspond to the growth parameter V_g/ G < ξ_crit.

With allowance made for the experimental data on the range of the formation of A-microdefects, the calculations were carried in the range from 1223 to 1023 K [10]. It is assumed that, in the high-temperature range (1682 K < T < 1223 K, the growth parameter is V_g/ G < ξ _crit), there occur nucleation and growth of impurity precipitates. In this range, the supersaturation of intrinsic point defects (intrinsic interstitial silicon atoms) is low and, hence, the nucleation rate of A-microdefects is negligible. At T≤ 1223 K, the supersaturation increases, which leads to an increase in the nucleation rate of A-microdefects. After the formation of A-microdefects, their growth is accompanied by a rapid consumption of intrinsic interstitial silicon atoms. As a result, the supersaturation decreases and the nucleation rate of A-microdefects decrease drastically. Consequently, the nucleation dominates in a narrow temperature range, and, therefore, the nucleation of A-microdefects outside the zone of their formation is ignored. Moreover, since the growth rate of A-microdefects decreases sharply with an increase in their size and the corresponding decrease in the concentration of intrinsic interstitial silicon atoms, the growth of A-microdefects outside the nucleation zone is also disregarded.

Detailed calculations are presented in the articles [68]. The temperature of the formation of A-microdefects corresponds to ~1153 K. An increase in the crystal growth rate weakly decreases the critical radius of A-microdefects and slightly affects the nucleation temperature. An increase in the crystal growth rate leads to an almost twofold decrease in the concentration of introduced defects.

The data of the computational experiment on the determination of the microvoid concentration correlate well with the experimentally observed results (10⁴-10⁵ cm^-3) [36]. For the A-microdefects, for which the concentration according to the experimental data is ~10⁶…10⁷ cm^-3 [14], the discrepancy is as large as three orders of magnitude. This can be explained by the fact that, unlike microvoids, which are formed only through the coagulation mechanism, the formation of A-microdefects occurs according to both the coagulation mechanism and the mechanism of prismatic extrusion (deformation mechanism) [14]. The results of the calculations suggest that the main contribution to the formation of A-microdefects is made by the mechanism of prismatic extrusion when the formation of interstitial dislocation loops is associated with the relieving of stresses around the growing precipitate. Consequently, the impurity precipitation processes that proceed during cooling of the crystal from the crystallization temperature are fundamental (primary) in character and determine the overall defect formation process in the growth of dislocation-free silicon single crystals.

The calculations of the formation of microvoids and interstitial dislocation loops (A-microdefects) demonstrated that the above assumptions do not lead to substantial differences from the results of the previous calculations in terms of the model of point defect dynamics. This circumstance indicates that the mathematical model of point defect dynamics can be adequately used on the basis of the physical model in which the impurity precipitation process occurs before the formation of microvoids or interstitial dislocation loops. Consequently, the model of the dynamics of point defects can be considered as component part of the diffusion model for formation grown-in microdefects. Moreover, the significant result of the calculations is the confirmation of the coagulation mechanism of the formation of microvoids and the deformation mechanism of the formation of interstitial dislocation loops.

6.3. Model of the Vacancy Coalescence

We have proposed a new alternative mathematical model of formation secondary grown-in microdefects (microvoids) in dislocation-free silicon single crystals. It is shown that microvoids are formed in a narrow temperature range of 1403…1343 К [70]. This is caused by a sharp decrease in the concentration of background impurity which does not form agglomerates (they arise in the temperature range of 1683…1423 K upon crystal cooling [59]).

This model explains the excess of nonequilibrium vacancies upon crystal cooling during growth and the absence of microvoids in crystals with small diameters. A possible reason for the excess of nonequilibrium vacancies is the bonding of oxygen atoms into grown-in microdefects ((I+V)-microdefects) with a decrease in temperature to T <1423 K. Under such conditions, the decay of the supersaturated solution of vacancies and vacancy diffusion occur simultaneously in the first stage. When most vacancies are spent on the microvoid formation and the concentration of nonequilibrium vacancies becomes fairly low, the diffusion of the remaining nonequilibrium vacancies to the surface and into the bulk of the crystal is accompanied by microvoid coalescence. When this second stage is over, all excess vacancies emerge on the crystal surface [70].

In the first stage, this system can be described by the equations [70]:

where n is the nonequilibrium-vacancy concentration, is the vacancy diffusion coefficient, r is the microvoid radius, N_L is the vacancy concentration in a microvoid (or inverse volume per vacancy), and N is the experimentally observed microvoid concentration [34].

The boundary and initial conditions have the form n|x=0,n|t=0=n0, at x≤δ0,at x>δ,r|0=0,d|t=0=∞

The condition n|x=0=0 assumes that the excess vacancies are very rapidly absorbed on the surface [70]. The surface (х = 0) is arbitrarily considered to be the crystal layer corresponding to Т = 1403K. The condition of infinite crystal diameter d|t=0∞ ( ) implies that the drain of vacancies from the crystal bulk to the lateral surface is neglected.

To solve the problem for the first stage, we will substitute (88) into (87), integrate over time, and introduce new variables:

where μ6=NL2n018/3πN2,v=μ2D,λ=μ−48/3πN−2

In this case, Eqs. (87) and (88) become dimensionless:

where

with the boundary and initial conditions q|r=0,q|ξ=0,q|ξ=∞,=0. . The function is found by substituting the initial conditions into Eq. (90).

The first stage duration q₁ depends on the drift time of most excess vacancies to pores, which is found from Eq. (90) with the exclusion of the diffusion term ∂2q∂ξ2, , which is approximately unity. One necessary condition of pore formation in a layer of thickness δ is the limitation τ1≤τs=Δ2 . In accordance with this condition, the pore formation time should not exceed the time that the vacancy drifts to the surface. The characteristic times of the first stage in the dimensional form can be written as

The stationary profile pores after the first stage ∂q/∂τ≈0 can be determined from the equation

with the boundary conditions q|ξ=0,=q|ξ→∞=0. The parameter determining the shape of the pore profile is the quantity Δ: the ratio of the characteristic time it takes the vacancy to drift to the surface to the characteristic pore formation time. The solutions to Eq. (95) for the three ranges of change in the coordinate x have the form

where ξmax=∫0qmaxdq225q5/2−q+qΔ,ξ0400qΔ1/4−Δ,

q Δ,q _maxare determined from the equation 25qmax5/2−qmax+qΔ=0,∫qΔqmaxdq225q5/2−q+qΔ,Δ−ξmax.

The duration of the second stage (pore coalescence) can be estimated using the expression for the coalescence characteristic time,

where s is the surface tension at the crystal/vacuum interface, R is the void radius, Ω is the volume per vacancy and is the equilibrium void concentration.

When the impurity diffuses throughout the crystal, it decorates the vacancy profile if the time it takes to pass the distanceδ(t_imp) is shorter than t_II . Therefore, the condition for impurity profile formation has the form

where D_imp is the impurity diffusion coefficient.

Detailed calculations are presented in the articles [70]. The estimation of the characteristic times of the first and second stages, which is performed for the temperature range of microvoid formation, showed that the relation t₁<<t_S<<t_II is satisfied. Hence, one can unambiguously conclude that a quasi-stationary pore profile is formed during silicon crystal growth if an excess vacancy concentration arises in the range of crystal cooling from 1403 to 1343 K. The conditions for decorating microvoids by background carbon and oxygen impurities (100) in the temperature range of 1343…1173 К [34, 36] are satisfied well. Our results confirm that an increase in temperature reduces the probability for decorating the pore profile by impurity.

When stating the problem, we disregarded the vacancy drain to the lateral crystal surface. The lateral surface limits the conditions for forming microvoids in the crystal cross section from below:d_min2 > δ . Therefore, under certain temperature conditions, microvoids should be formed in real commercial single crystals during growth if the crystal diameter exceeds 80 mm.

The fundamental interaction between impurities and intrinsic point defects upon crystal cooling under certain thermal conditions ( T < 1423 K ) leads to impurity depletion and the formation of a supersaturated solid solution of intrinsic point defects. The decay of this supersaturated solid solution causes the coagulation of intrinsic point defects in the form of microvoids or interstitial dislocation loops in different regions of the crystal.

An analysis of the experimental and calculated data within model of the vacancy coalescence in accordance with

the heterogeneous diffusion model of the formation of grown-in microdefects revealed the following reasons for the occurrence of microvoids in dislocation-free silicon single crystals:

(i) a sharp decrease in the concentration of background impurity that was not associated into impurity agglomerates (formed in the cooling range of 1683…1423 К);

(ii) a large (over 80 mm) crystal diameter (in this case vacancies fail to drain from the central part of the crystal to the lateral surface);

(iii) crystals of large diameter generally contain a ring of D-microdefects which forms due to the emergence of the (111) face on the crystallization front and which depletes the region inside with impurity atoms.

The growth parameter V_g/G describes the fundamental reasons related to the systematic nonuniform impurity distribution during crystal growth from a melt. Based on an analysis of the experimental results, one can suggest that the parameter V_g/G controls the growth because it describes the condition for the emergence of the (111) face at the crystallization front. Therefore, the impurity depletion inside the ring of D-microdefects upon crystal cooling at T < 1423 K is caused by two things: the impurity bonding during the formation of primary grown-in microdefects ((I+V)-microdefects) and the impurity drift to the (111) face, which is equivalent to the annular distribution of primary D-type grown-in microdefects. In this case, excess vacancies arise within the ring of D-microdefects to form a supersaturated solid solution with its subsequent decay and the formation of vacancy microvoids. In contrast, excess silicon self-interstitials arise beyond the D-ring to form a supersaturated solid solution with its subsequent decay and the formation of interstitial dislocation loops (А-microdefects) [70].