INTRODUCTION

In recent years increasing attention has been given towards the study of rock salt, CsCl, diamond and zinc blende structured solids. Alkali halides and alkaline-earth chalcogenides have attracted attention of physicists due to many practical uses and rock-salt crystal structures. Alkaline earth chalcogenides are important in geophysical science and research since they are link between the highly ionic alkali halides and covalent III-V compounds [1]. According to the classical valence picture, all the elements from column IV of the periodic table (C, Si, Ge and Sn) should be capable of forming diamond-type crystals. Each atom has four valence electrons, which occupy the tetrahedrally hybridised sp³ orbitals pointing towards the four nearest neighbours and this is true for C through Sn. Most of the semiconductors that are used in the modern microelectronic industry have the zinc blende crystallographic structure. The crystals with zinc blende or sphalerite structure range from raw iron and zinc minerals to man-made GaN and BN semiconductors. The particular omnitriangulated nature in atomic structure gives these materials unique physical properties. Recently [2-6], there is an attractive considerable interest on II-VI semiconductors and their alloys due to their application in photovoltaic devices, as electro-optic crystals with ultra fast response time spectroscopy and recent realization of light-emitting diodes (based on ZnTe). This has motivated several theorists to modelling band offset [7], structural and thermo dynamical properties in this family and their alloys [8,9] and to revise many fundamental physical properties based on ab initio calculations [10]. In fact, the role of metal d-states in II-VI semiconductors is very important. Wei and Zunger [11], have shown that p-d repulsion and hybridisation (i) lower the band gaps, (ii) reduce the cohesive energy, (iii) increase the equilibrium lattice parameters and also have an influence on other features.

A considerable amount of experimental and theoretical work has been done during the last few years on the bulk modulus and cohesive energies of these semiconductors and insulators. Modern computational methods have made it possible to study the structural, mechanical and optical properties of a wide variety of molecules and solids in great detail. There are however, instances where this level of detail either cannot be easily attained because of the complexity of the system or is not needed, as when studying broad trends in the behaviour of a large set of systems. Empirical concepts such as valence, empirical radii, electronegativity, ionicity and plasmon energy are then useful [12,13]. These concepts are directly associated with the character of the chemical bond and thus provide means for explaining and classifying many basic properties of molecules and solids.

Therefore, we thought it would be of interest to give an alternative explanation for bulk modulus and cohesive energies of rock salt, CsCl, diamond and II-VI zinc blende structured solids. In this paper we propose a method based on a plasma oscillations theory of solids for the calculation of the bulk modulus (B in GPa), and cohesive energy (E_coh in kcal/mol) of these semiconductors and insulators. It is now well established that the plasmon energy of a metal changes [14, 15], when it undergoes a chemical combination and forms a compound. A plasmon is a collective excitation of the conduction electrons in a metal with energy, ħω_p, which depends on the density of the conduction electrons. This is due to the fact that the plasmon energy depends on the density of the conduction electrons and effective number of valence electrons, which changes when a metal forms a compound. We have calculated the bulk modulus (B in GPa), and cohesive energy (E_coh in kcal/mol) in rock salt, CsCl, diamond and II-VI zinc blende structured solids using this idea.

The present paper is an extension of our earlier work [16], where the mechanical and optical properties of A^IB^IIIC₂^VI and A^IIB^IVC₂^V semiconductors of the chalcopyrite structural type were quantitatively calculated using plasmon oscillations theory of solids, and we have shown that this theory is a widely applicable method in calculating or predicting mechanical and optical properties such as microhardness, bulk modulus, dielectric constant, electronic polarizability and susceptibility of crystal materials. However, one of the most important aspects of this method is that the detailed crystal structures of the materials to be studied must be clearly known.

THEORETICAL CONCEPTS

A metallic crystal may be described as an assembly of immediate positive ion cores and conduction electrons that are nearly free to move over the whole of the crystal. The condition of charge neutrality is maintained because of the balance struck between the negative charge on conduction electrons and an equal concentration of positive charge on ion cores. Thus a metal serves as a good example of plasma. A random motion may be a momentary fluctuation in the equilibrium position of an electron, caused by the average electrostatic field of all other electrons. The position fluctuation would create a charge imbalance in the region of that electron, as a result of which other electrons would rush into that region in order to restore the condition of charge neutrality. At any finite temperature, electrons being very light particles move with fairly large speed relative to ions which we consider to be at rest. The electrons rushing into the region of the electron that suffered a fluctuation in its equilibrium position are unable to stop at the desired positions and overshoot their mark on account of the large kinetic energy which by the way represents the total energy there. As soon as the energy goes totally electrostatic, electrons turn around and attempt again to approach the wanted locations in the region of the misbehaving electron. The repetition of this process constitutes the collective oscillatory motion. These collective oscillations are called plasma oscillations. The energy of a quantum of plasma oscillations of the valence electrons in both metal and compound is given by the relation [17],

where Z is the number of electrons taking part in the plasma oscillations, σ the specific gravity and W the molecular weight. Equation (1) is valid for free electrons but it is also applicable for semiconductors and insulators, up to a first approximation. Raether [18], and Philipp and Ehrenreich [19] have shown that the plasmon energy for semiconductors and insulators is given by, where δε_o is a very small correction to the free-electron plasmon energy ħω_p and can be neglected to a first approximation. Philipp and Ehrenreich [19] have shown that the calculated values of ħω_p and ħω_pd are in fair agreement with their observed values of plasmon energy in dielectrics. It has also been pointed out by Kittel [20] that the plasmon oscillations in dielectrics are physically the same as in metals.

Presently, Srivastava [21-23] has studied electronic properties for rock salt, zinc blende and CsCl structured solids in terms of plasmon energy (ħω_p) by the following relations,

Here E_h, E_c and d are homopolar gaps, ionic gaps and bond length respectively, K₁, K₂, K₃, K₄ and ν are constants depending upon the structure elements and b is prescreening factor. Recently, Kumar et al. [13], have shown that heat of formation for A^IB^IIIC₂^VI and A^IIB^IVC₂^V semiconductors may be determine in terms of plasmon energy by following form,

where C and C’ are constants.

In previous work [16], we have evaluated mechanical and optical properties such as microhardness (H), bulk modulus (B), dielectric constant (ε), electronic polarizability (α) and susceptibility (χ) for chalcopyrites in terms of plasmon energy ħω_p (ħω_p in eV)_, for A^IIB^IVC₂^V

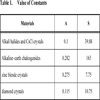
for A^IB^IIIC₂^VI for A^IB^IIIC₂^VI and A^IIB^IVC₂^V for A^IB^IIIC₂^VI and A^IIB^IVC₂^V for A^IB^IIIC₂^VI and A^IIB^IVC₂^V where S, V and D are constants, which depends upon group of materials. Similarly, based on the above expressions, we are of the view that some parameters related to ground state properties (i.e. bulk modulus and cohesive energy) of rock salt, CsCl, diamond and II-VI zinc blende structured solids can be evaluated using their plasmon energy (ħω_p in eV) by following relations, and where A, Aʹ, S and Sʹ are the numerical constants depending upon the structure element (i.e. group of materials). These values are Aʹ = 2 for rock salt, CsCl and zinc blende crystals, Aʹ = 2.4 for diamond crystals, Sʹ = 0.56 for rock salt and CsCl crystals and Sʹ = 0.99 for zinc blende and diamond crystals. The values of A and S are listed in Table 1.

RESULTS AND DISCUSSION

The bulk modulus and cohesive energy are important ground state properties of a material; bulk modulus defines its resistance to volume change when compressed. Both experimental and theoretical results suggest that the bulk modulus reflects the hardness of the materials [24, 25]. Jayaraman et al. [26] predicted that the bulk modulus directly depends on the product of the ionic charges. Any change in crystallographic environment of an atom is related to core electrons via the valence electrons. The change in wave function that occurs for the outer electrons usually means a displacement of electric charge in the valence shell so that the interaction between valence, shell, and core electrons is changed. This leads to a change in binding energy of the inner electron and to a shift in the position of the absorption edge. plasmon energy also depends on the effective number of valence electrons and density of the conduction electrons, which changes when a metal forms a compound.

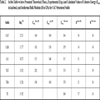
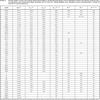
According to this idea, we have proposed relations (4) and (5) for the calculation of bulk modulus and cohesive energy of alkali halides, cuprous halides, thallous halides, alkaline–earth chalcogenides, group IV and II-VI semiconductors. The values so obtained are presented in the following Tables 2 and 3 compared with the experimental and theoretical data reported so far. For example the results for bulk modulus differ from experimental by, LiCl–0%, C–0%, Si–0% and ZnS–0%, and the results for cohesive energy differ from experimental by LiF–0%, KF–0%, KCl–0%, KBr–0%, KI–0%, RbBr–0% and RbI–0% in the current study. We note that proposed approach is quite reasonable and can give us a useful guide in calculating and predicting the bulk modulus and cohesive energy of crystal materials. Thus it is possible to predict the order of bulk modulus and cohesive energies of semi conducting and insulating compounds from their plasmon energies. The present approach for the calculation of the ground state properties of solids can be used for semi conducting and insulating compounds without having knowledge of crystal ionicity, transition pressure, while the model given by Neumann [27], and Al-Douri et al. [28] requires the values of these parameters to calculate the bulk modulus of solids and is limited to the simple binary compounds.

CONCLUSION

From the above results obtained by using the proposed approach, it is quite obvious that the parameters such as bulk modulus (B in GPa), and cohesive energy (E_coh in kcal/mol) reflecting the ground state properties, can be expressed in terms of plasmon energies of these materials, which is definitely a surprising phenomenon. The calculated values are presented in Tables 2 and 3. We note that calculated values are in close agreement with values determined directly from experiment. The various parameters evaluated in this work hardly deviates 0% to 6% and the maximum discrepancy for bulk modulus is 9% in the case of Ge from the experimental data. The values evaluated show a systematic trend and are consistent with the available data reported so far, which proves the validity of the approach. Since we have been reasonably successful in calculating these parameters using the plasmon frequency of the materials for chalcopyrite crystals (A. S. Verma et al. [16]), it is natural to say that this approach can easily be extended to rock salt, CsCl, diamond and zinc blende crystals. Hence it is possible to predict the order of ground state properties of semi-conducting and insulating compounds from their plasmon energies.