The magnetic flux penetration into a type-II superconductor occurs in the form of quantized vortices. In the presence of different types of defects or pinning centers in the superconductor sample, the vortices may be attached to such defects. A nature of interaction between the vortices and the structural defects is determined by the pinning force F_P. If transport current with the density j is passed through superconductor, the interaction of the current with vortex lines leads to the emergence of the Lorentz force F_L, acting on each one of the vortices. Under the effect of the Lorentz force F_L the viscous flux flow of vortices begin to move. The viscous magnetic flux flow in accordance with electromagnetic induction creates a vortex electric field E. This means that energy dissipation occurs, an electric resistance appears and the superconductor undergoes a transition to the resistive or to the normal state. Propagating magnetic flux causes Joule heating, giving rise to global and/or micro flux avalanches in the critical state of type-II superconductors. Thus, flux jumps results in a large-scale flux avalanches in a superconductor and their origin are related to the magnetothermal instabilities [1-5]. Thermomagnetic instability or flux jump phenomena have been observed in conventional hard superconductors [1-6], as well as in high-temperature superconductors, recently [7, 8]. The critical state stability against flux jumps in hard and composite superconductors has been discussed in a number of theoretical and experimental papers [1-5]. The general concept of the thermomagnetic instabilities in type-II superconductors was developed in literature [4, 5]. The dynamics of small thermal and electromagnetic perturbations, whose development leads to the flux jump, have been investigated theoretically in detail by Mints and Rakhmanov [5]. The authors have found the stability criterion for the flux jumps in the framework of adiabatic and dynamic approximations in the viscous flux flow regime of type-II superconductors. Conventionally, thermomagnetic instabilities were interpreted in terms of thermal runaway triggered by local energy dissipation in the sample [5]. According to this theory, any local instability causes a small temperature rise, the critical current is decreased and magnetic flux moves much easily under the Lorentz force. The additional flux movement dissipates more energy further increasing temperature. This positive feedback loop may lead to a flux jumps in the superconductor sample.

In our previous work, the dynamics of small thermal and electromagnetic perturbations has been studied in the flux flow regime, where voltage current-current characteristics of hard superconductor is described by linear dependence of j(E) at sufficiently large values of electric field [9]. In the region of weak electric fields the current-voltage characteristics j(E) of superconductors is highly nonlinear due to thermally activated dissipative flux motion. A theoretical analyze of the flux jumping in the flux creep regime, where the current-voltage characteristics of a sample is a nonlinear have been carried out recently by Mints [10] and by Mints and Brandt [11]. However, a careful study the dynamics of the thermal and electromagnetic perturbations in the regime weak electric field with nonlinear current-voltage characteristics associated with flux creep is still lacking.

In the present paper the spatial and temporal evolution of small perturbations of the temperature and electromagnetic field in the flux creep regime for the simplest geometry, i.e., in a superconducting slab placed in a parallel magnetic field is considered. We shall study the problem in the framework of a macroscopic approach, in which all lengths are larger than the flux-line spacing; thus, the superconductor is considered as a uniform medium.

We study the evolution of the thermal and electromagnetic penetration process in a simple geometry - superconducting semi-infinitive sample x≥0. We assume that the external magnetic field induction B_e is parallel to the z-axis and the magnetic field sweep rate B_e is constant. When the magnetic field with the flux density B_e is applied in the direction of the z-axis, the transport current δj(x,t) and the electric field δE(x,t) are induced inside the slab along the y-axis. For this geometry, the temporal and spatial evolution of thermal δT(x,t), electromagnetic field δE(x,t) and current δj(x,t) perturbations are described by the following nonlinear heat diffusion equation [9-11]

Here j_c is the critical current density, ν=ν(T) and κ=κ(T) are the specific heat and thermal conductivity, respectively. In order to obtain analytical results of a set Eqs. (1), (2), we suggest that j_c is independent on magnetic field induction B and use the Bean's [1] critical state model j_c = j_c(B_e,T)

jc(T)=jc(T0)1−T−T0Tc−T0,

where T₀ and T_c are the equilibrium and critical temperatures of the sample, respectively [9]. For the sake of simplifying of the calculations, we perform our calculations on the assumption of negligibly small heating T-T₀ << T_c-T₀ and assume that the temperature profile is a constant within the across sample and thermal conductivity κ and heat capacity ν are independent on the temperature profile. We shall study the problem in the framework of a macroscopic approach, in which all lengths scales are larger than the flux-line spacing; thus, the superconductor is considered as a uniform medium.

The set of differential equations (1), (2)) should be supplemented by a current-voltage curve j=j(E,B,T). In the flux creep regime the current-voltage characteristics of type - II conventional superconductors is highly nonlinear due to thermally activated dissipative flux motion [12, 13]. For the logarithmic current dependence of the potential barrier U(j), proposed by [14] the dependence j(E) has the form

where E_c = const and the parameter n depends on the pinning regimes and can vary widely for various types of superconductors. In the case n=1 the power-law relation (3) reduces to Ohm's law, describing the normal or flux-flow regime [6]. For infinitely large n, the equation describes the Bean critical state model j = j_c [1]. When 1<n<∞, the equation (3) describes nonlinear flux creep [14]. In this case the differential conductivity σ is determined by the following expression

It is assumed, for simplicity, that the value of n temperature and magnetic-field independent. It should be noted that the nonlinear diffusion-type equations (1) and (2), completed by the flux creep equation (4), totally determine the problem of the space-time distribution of the temperature and electromagnetic field profiles in the flux creep regime with a nonlinear current-voltage characteristics (3) in a semi-infinite superconductor sample.

To find an analytical solution of Eqs. (1) and (2) we use simple adiabatic approximation, assuming that τ<<1, i.e., that the magnetic flux diffusion is faster than the heat flux diffusion [4, 5]. Therefore, we neglect the diffusive term in the heat equation. Then eliminating the variable δT(x,t) by using the relationship (1) and substituting into Eq. (2), we obtain a second-order differential equation for the distribution of small electromagnetic perturbation e(x,t) in the form

Here, we introduced the following dimensionless variables

z=xL,τ=tt0,ϵ=δEEc,t0=μ0jcL2Ec,β=μ0jc2L2ν(Tc−T0),γ=1−nn.

Here L=cHe4πjc is the magnetic field penetration depth. Since we have neglected the redistribution of heat in deriving Eq. (5), only the electrodynamic boundary conditions (see, Ref. [9]) should be imposed on this equation

The solution of (5) together with the boundary conditions (6) can be obtained by using the method of separation of variables. Looking for the solution of Eq. (5) in the form

we get the following expressions for a new variables

By integrating equation (8) we easily obtain

where τ_p is the constant parameter, describing the characteristic time of magnetic flux penetration profile; k=1/γ. Now, integrating twice, the ordinary differential equation for the function φ(z) with the boundary conditions (6) and taking into account (10), we find the following an explicit solution of (5) in the form [15]

The obtained solution (11) describes the distribution of the electromagnetic field in the flux creep regime with a power-law current-voltage characteristics. The solution describes an blow-up-type instability in the superconductor sample. As easily can be seen that the solution remains localized within the limited area x<L^*/2 with increasing infinitively of time. This characteristic phenomenon often occurring in nonlinear parabolic problems is blow-up of solutions in finite time [15]. In other words, the growth of the solution, becomes infinite at a finite time τ_p. Typical distributions of the electric field e(z,t) determined from analytical solution (11) is shown in Fig. (1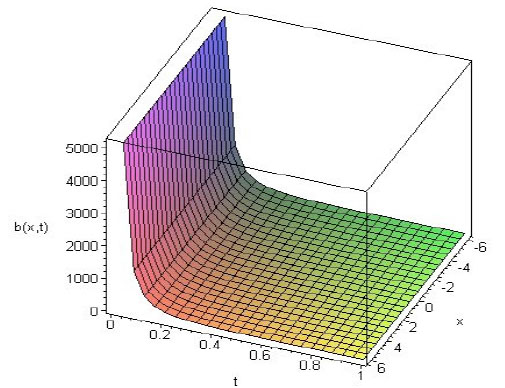) for the values of parameters τ_p=1, n=2, β ~ 0.5 and L^* ~ 1.

Fig. (1) The space and time evolution of the electric field profiles at different times for τp=1, n=2, β~0.5 and L* ~ 1.

In conclusion, we have performed a theoretical study of dynamics of small thermal and electromagnetic perturbations in type-II superconductors in the flux creep regime in the framework adiabatic approximation [5]. For this purpose, the space-time evolution of temperature and electric field was calculated using the heat diffusion equation, coupled with Maxwell’s equations and material law, assuming that heat diffusion is small that the magnetic diffusion. An explicit solution of the diffusion equation has been obtained, which describes the distribution of the electromagnetic field in the flux creep regime with a power-law current-voltage characteristics.