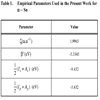
The empirical parameters included in the LUC-INDO method are the orbital exponent ζ, the bonding parameterβo,12Is+As,and12Ip+Ap. The symbols I and A refer to the ionization potential and the electron affinity respectively. The optimum values of these empirical parameters used for α - Sn in the present work are listed in Table 1. The value of the orbital exponent ζ determines the charge distribution of electrons around the nucleus. This parameter is varied till the total energy reaches its minimum value. As a consequence, this parameters is chosen in the same way of the ab initio methods. Comparing the ζ value for α - Sn crystal with that obtained by Clementi and Roetti (1.89 a.u^-1 [28] for atoms, shows that the ζ value for solids is larger than that for atoms. This indicates the contracted charge distribution for solids and the diffuse charge distribution for atoms. The absolute value of the bonding parameter β^° of α - Sn crystal is noted to be much smaller than that for molecules (-11.85 eV) [29]. This can be explained by noting that the number of bonds in solid is higher, then the interaction energy is distributed over all these bonds. The value of the 12Is+As parameter of α - Sn crystal is less than the corresponding value of the tin free atom. This indicates that the s orbitals of the solid are less connected to their atoms than in the free atom. A reverse observation is reported for the 12Ip+Ap parameter.

Table 1

Empirical Parameters Used in the Present Work for α - Sn

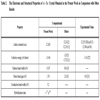
Using the computational procedure described in section 2, the electronic and structural properties of α - Sn crystal at 0 K and zero pressure are calculated as listed in Table 2 in comparison with other computational and experimental results.

Table 2

The Electronic and Structural Properties of α - Sn Crystal Obtained in the Present Work in Comparison with Other Results

The equilibrium lattice constant (a₀) is determined by plotting the total energy as a function of the lattice parameter, as depicted in Fig. (1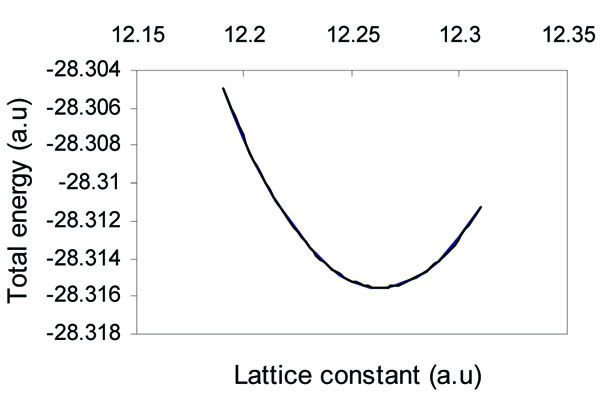). The calculated value of the equilibrium lattice constant (12.263 a.u) is in good agreement with the estimated value of 12.184 a.u from the experimental data [30].

Fig. (1) Total energy of (α - Sn) as a function of lattice constant.

The cohesive energy is calculated from the total energy of the large unit cell. Since the large unit cell in the present work is composed of 8 atoms, the cohesive energy can be determined from the following expression:

where E_free denotes the free atom sp shell energy, E₀ is the vibrational energy state, which is referred to as zero-point energy, and its value is 0.03 eV [32]. The cohesive energy value of present work (-3.144 eV) is also in good agreement with the experimental value of -3.14 eV [31]. This is due to the including of the exchange integrals, correlation correction, and zero-point energy in the present analysis. The correlation correction is the correction included to take into account the fact that the motions of electrons are correlated pairwise to keep electrons apart. Correlation energies may be included by considering Slater determinants composed of orbitals that represent excited state contribution, and this method of including unoccupied orbitals in the many body wavefunction is referred to as configuration interaction (CI) [24]. Another method to estimate the correlation correction, which is used in the present work, is the Moller-Plesset perturbation theory [24]. This correction is calculated to be 0.27 eV. A detailed description of the several kinds of correlation corrections is present in reference [24].

The calculated direct band gap is considerably larger than the experimental value. A similar anomaly was also obtained by Svane [5] using the Hartree-Fock approximation. The large computed value of the direct band gap can be attributed to the approximations involved in the LUC-INDO formalism and Hartree-Fock method, and to the perturbative treatment of the correlation correction [33]. However, the available non-perturbative correlation correction method takes nearly ten times the computational time needed in Moller-Plesset method. The most significant approximations that affect the band gap are:

1. Using equal values of ζ and β^° for s and p wavefunctions. The difference between bonding and anti-bonding states is directly proportional to β^°S, where the overlap integral S is a function of ζ. The percentage different of ζ between s and p orbitals was reported to be 14.4% for tin [28].
2. Neglecting the core states will also result in a neglect of its effects on the distribution of the outer valence electrons.
3. Using the 5s 5p orbitals only without the inclusion of the 4d orbital.

It should be pointed out that the present value for the band gap is a non-relativistic value. The computed band gap value of tin is expected to be in good agreement with the corresponding experimental value if the relativistic splitting of the levels [5] is considered, and if greater size of LUC is used [34], in addition to the points mentioned above.

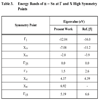
The eigenvalues of the high symmetry points used to determine the band structure are listed in Table 3, in comparison with the corresponding values calculated by Svane [5].

Table 3

Energy Bands of α - Sn at Г and X High Symmetry Points

Some physical properties of solids can be determined using the analysis described in the preceding section, such as the electronic charge density and the X-ray scattering factor, the valence electrons charge density (ρ_e(r)) can be expressed as:

The electronic charge density for some planes of α - Sn crystal is displayed in Fig. (2).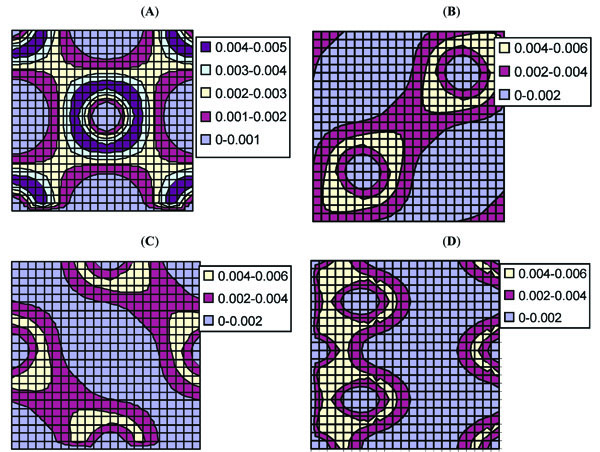

Fig. (2) Valence charge density (in atomic unit) of α - Sn in the: (A) (001) plane, (B) (400) plane, (C) (200) plane, and (D) (110) plane.

The X-ray scattering factor (f_j) is defined by [31].

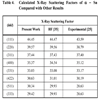
where G is the reciprocal lattice vector. In Table 4, the calculated X-ray scattering factors for α - Sn are listed in comparison with other computational [35] and experimental [25] results. The calculated X-ray scattering factors are in good agreement with the experimental values.

Table 4

Calculated X-Ray Scattering Factors of α - Sn Compared with Other Results

The pressure dependence of the electronic structure can be predicted from the present computational analysis. The pressure dependence of the lattice parameter is determined using the Murnaghan [36] equation of state:

where a is the lattice parameter at pressure P, a_o is the lattice constant at zero pressure, B_o is the bulk modulus at zero pressure, and 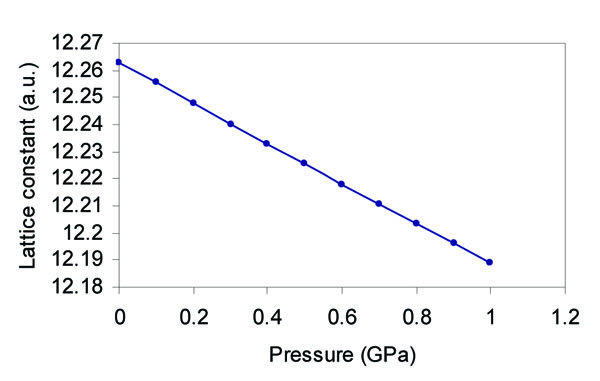B_ represents the pressure derivative of the bulk modulus and its value for α - Sn is 4.6 [37]. The variation of the lattice parameter as a function of pressure for α - Sn is depicted in Fig. (3). This figure was plotted using the experimental value of B₀ of 53 GPa [38] and the calculated value of B_ of 4.6 [37].

Fig. (3) Lattice constant of (α - Sn) as a function of pressure.

The pressure dependence of the cohesive energy, direct band gap, valence band width, and conduction band width as predicted from our analysis is shown in Figs. (4-7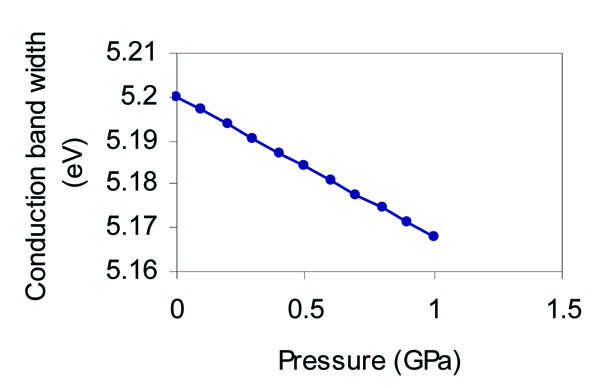) respectively.

Fig. (4) Effect of pressure on the cohesive energy of grey tin.

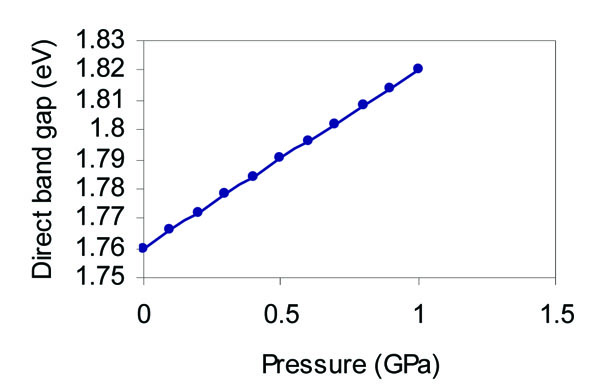Fig. (5) Effect of pressure on the direct band gap width of grey tin.

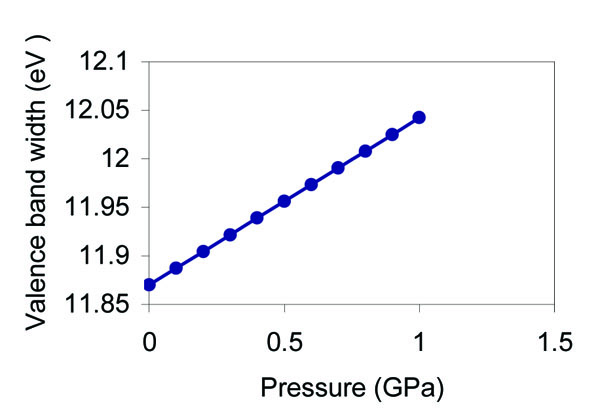Fig. (6) Effect of pressure on the valence band width of grey tin.

Fig. (7) Effect of pressure on the conduction band width of grey tin.

As it is obvious from Fig. (5), the direct band gap increases nearly linearly with the increase of the pressure. We suppose that this is mainly due to the nearly linear dependence of the lattice constant with the pressure as shown in Fig. (3), and since the translation vector (T_v) scales linearly with the lattice constant, one can expect a nearly linear relation between the band gap and the pressure according to the present model. The pressure derivative of the direct band gap equals 0.06 eV/GPa. Wei and Zunger [37] have determined the pressure derivative of the band gap of the three main transitions; Г- X, Г- L, and Г- Г for α - Sn to be -0.01, 0.059, and 0.166 eV/GPa respectively. The direct band gap is determine, d from the energy difference (Г₂-Г₂₅). The observed linear increase of the direct band gap with pressure is due to the linear increase of the Г₂ energy with respect to the Г₂₅ energy as found from the present analysis, and also by Bassani and Liu [3]. The valence band width is calculated from the energy difference (Г₂₅-Г₁). The Г₁ state is shown to decrease linearly with the increase of pressure, and this causes a linear increase of the valence band width as depicted in Fig. (6). The conduction band width can be determined from the energy difference (X_4c-Г₂). Although the X_4C energy is shown to increase with pressure, the conduction band width decreases with pressure as shown in Fig. (7) because the increase of Г₂ energy is more than the increase of X_4C energy.

It is found that the s state occupation decreases with the increase of pressure as in Fig. (8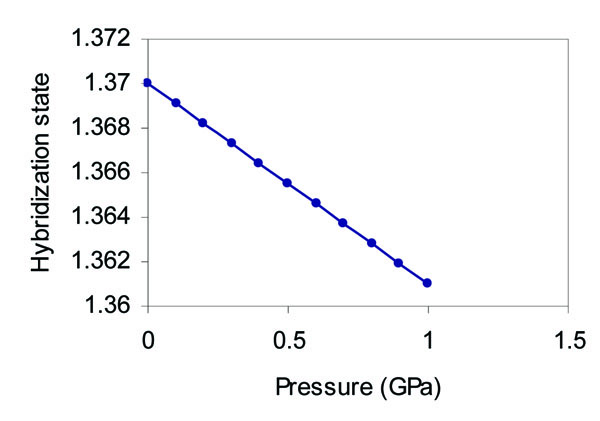), whereas the p state occupation increases with the increase of pressure as in Fig. (9).

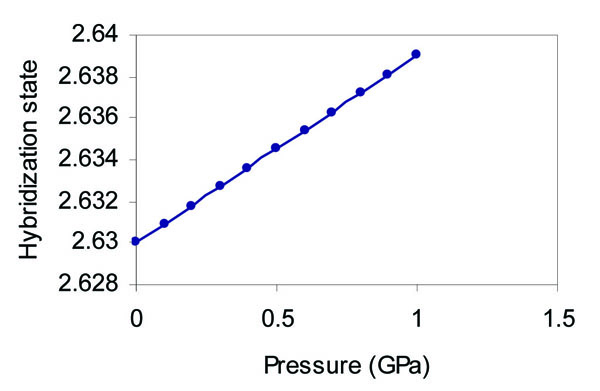Fig. (8) Effect of pressure on the hybridization state of the s orbital of grey tin.

Fig. (9) Effect of pressure on the hybridization state of the p orbital of grey tin.

The present works shows that the X-ray scattering factors decrease as pressure increases. This behavior is obvious in Table 5. This can be interpreted as follows: increasing pressure decreases the inter-planer distance (d_hkl), this increases the Bragg scattering angle (Bragg's law), and this in turn causes a decrease of the scattering wave intensity.

Table 5

Effect of Pressure on the X-Ray Scattering Factors of α - Sn