- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Cybernetics & Systemics Journal
(Discontinued)
ISSN: 1874-110X ― Volume 12, 2018
The Optimal Isolation Strategy for Network Public Opinion with Enclosed Environment
Kuan Yang*, Sasa Yu
Abstract
Public opinion dissemination control is of crucial importance to facilitate reliable and efficient data delivery, especially in networks consisting of openness, sharing and convenience. From a systematic point of view, we aim to explore the optimal control policy for information dissemination with relatively enclosed environment. To control the effusion of network public opinion is more important than deleting existing information about it. We depict the impact of isolation strategy on the transmission dynamics of network public opinion. Since the abstraction of information dissemination much resembles the spread of epidemics, a simplified SLIR model is utilized to characterize the collective dynamics of information dissemination over networks. Moreover, an optimal objective based on the maximum social utility is established, namely, minimizing both the total outbreak size of public opinion and the relevant costs of isolations. The optimal solution is acquired by using the Pontryagin’s Maximum Principle. Lastly, the simulations to the opinion control efficacy are accomplished, so the effectiveness of the control methods in the network public opinion is verified.
Article Information
Identifiers and Pagination:
Year: 2016Volume: 10
First Page: 242
Last Page: 249
Publisher Id: TOCSJ-10-242
DOI: 10.2174/1874110X01610010242
Article History:
Received Date: 15/03/2016Revision Received Date: 06/10/2016
Acceptance Date: 06/10/2016
Electronic publication date: 25/11/2016
Collection year: 2016
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
* Address correspondence to this author at the School of Business Administration, Hunan University, Changsha, Hunan 410082, China; Tel: +8618900739680; E-mails: yangkuan@hnu.edu.cn, yss@hnu.edu.cn
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 15-03-2016 |
Original Manuscript | The Optimal Isolation Strategy for Network Public Opinion with Enclosed Environment | |
1. INTRODUCTION
At present, the network public opinion has become an important part of the whole social public opinion [1C. Su, J. Peng, and S. Li, "A survey on the mathematical modeling of internet public opinion research both at home and abroad", J. Intell., vol. 33, no. 10, pp. 14-20, 2014.]. Generally speaking, network public opinion is the public opinions of some event with some influence and strength [2Q. Zhang, F. Liu, and Y. Huang, "A warning and urgent decision-making mechanism for uncertain network public sentiment emergency", J. Comput. (Taipei), vol. 8, no. 10, pp. 2640-2647, 2013.]. More specifically, it is defined as the aggregation including people's socio-political attitudes, beliefs and values to both public issues and social managers, surrounding various social events through the network [3X. Hu, Y. Zhang, and B. An, "The mechanism and influencing factors of herding effect of college students' network public opinion", Anthropologist., vol. 23, no. 1,2, pp. 226-230, 2016.]. Social network era has put an unprecedented range of goods and information right at our fingertips. It promotes the network public opinion with the characteristics of being open, free, quick to transmit and spreading widely [4Y. Lan, and R. Zeng, "Research of emergency network public opinion on propagation model and warning phase", J. Intell., vol. 32, no. 5, pp. 16-19, 2013.]. Although network public opinion is essentially demands and expressions from separate individuals in public, fewer constraints for virtual crowd have greatly weakened the certainty and reliability of all kinds of information in network, especially for those about national development, social life and the interests of the individual information, etc. For instance, the salt-buying frenzy in China was caused by nuclear leakage in the Japan of 2011. This just derived from that iodized salt which could help to ensure people against nuclear radiation [5X. Zhao, and J. Wang, "Dynamical Model about Rumor Spreading with Medium. Discrete", Dyn. Nat. Soc., vol. 2013, pp. 1-9, 2013.
[http://dx.doi.org/10.1155/2013/586867] -8L. Zhao, Q. Wang, J. Cheng, D. Zhang, T. Ma, Y. Chen, and J. Wang, "The impact of authorities' media and rumor dissemination on the evolution of emergency", Physica A., vol. 391, no. 15, pp. 3978-3987, 2012.
[http://dx.doi.org/10.1016/j.physa.2012.02.004] ]. Likewise, the Malaysia Airlines flight MH370 accident in March 2014 had also led to a number of rumors in China, Southeast Asia, and other countries and regions [9Z. Zhao, Y. Liu, and K. Wang, "An analysis of rumor propagation based on propagation force", Physica A., vol. 443, pp. 263-271, 2016.
[http://dx.doi.org/10.1016/j.physa.2015.09.060] ].
The increasingly powerful influence of public opinion in network has drawn many scholars’ attention to take action [10D. Liu, W. Wang, and H. Li, "Evolutionary mechanism and information supervision of public opinions in internet emergency", Procedia Comput. Sci., vol. 17, pp. 973-980, 2013.
[http://dx.doi.org/10.1016/j.procs.2013.05.124] -13W. Chai, and M. Cheng, "The research on the network public opinion risk assessment based on the CWAHP-entropy method", Int. J. Secur. Appl, vol. 10, no. 4, pp. 197-208, 2016.]. Suo Shuguang and Chen Yu [14S. Suo, and Y. Chen, "The dynamics of public opinion in complex networks", J. Artif. Soc. Soc. Simul., vol. 11, no. 4, p. 2, 2008.] studied the problem of public opinion formation and concentrates in complex network. Juliane Urban and Kristin Bulkow [15U. Juliane, and B. Kristin, "Tracing public opinion online-an example of use for social network analysis in communication research", Procedia Soc. Behav. Sci., vol. 100, pp. 108-126, 2013.
[http://dx.doi.org/10.1016/j.sbspro.2013.10.703] ] theorized and measured public opinion building processes upon the Internet reliable. Ma Yaping and Shu Xueming et al. [16Y. Ma, X. Shu, S. Shen, J. Song, G. Li, and Q. Liu, "Study on network public opinion dissemination and coping strategies in large fire disasters", Procedia Eng., vol. 71, pp. 616-621, 2014.
[http://dx.doi.org/10.1016/j.proeng.2014.04.088] ] analyzed the importance for studying the network public opinion of large fire disasters. Wu Junhui, Ni Shunjiang and Shen Shifei [17J. Wu, S. Ni, and S. Shen, "Dynamics of public opinion under the influence of epidemic spreading", Int. J. Mod. Phys. C, vol. 27, no. 07, p. 1650079, 2016.
[http://dx.doi.org/10.1142/S0129183116500790] ] investigated propagation of public opinion in the case of avian influenza infection in humans. Moreover, internet public opinion transmission can be regarded as a social contagion process [18K. Kawachi, M. Seki, H. Yoshida, Y. Otake, K. Warashina, and H. Ueda, "A rumor transmission model with various contact interactions", J. Theor. Biol., vol. 253, no. 1, pp. 55-60, 2008.
[http://dx.doi.org/10.1016/j.jtbi.2007.11.024] [PMID: 18179802] ]. The epidemiological models were cited as seminal models in this area [14S. Suo, and Y. Chen, "The dynamics of public opinion in complex networks", J. Artif. Soc. Soc. Simul., vol. 11, no. 4, p. 2, 2008.]. D Gruhl and R Guha et al. [19G. R, L. David, T. A, "Information Diffusion Through Blogspace", In: Proceedings of the 13th international conference on World Wide Web, ACM, 2004, pp. 491-501.] developed a model for information diffusion based on the propagation theory of infectious diseases. The model divided people into three disjoint classes: susceptible, describing individuals who had not yet been aware of a particular network public opinion; infected, meaning individuals who transmit the public opinion through social interactions; and recovered, referring to individuals who had known the public opinion but choose not to spread it to others. For the information distortion during the transferring, people always have a thought process and do not spread it right now, Chen Bo and Yu Ling et al. [20B. Chen, L. Yu, J. Liu, and W. Chu, "Dissemination and control model of internet public opinion in the ubiquitous media environments", Xitong Gongcheng Lilum yu Shijian, vol. 31, no. 11, pp. 2140-2150, 2011.] took the subjective initiative into consideration, so the incubation period was introduced into the model, that is SEIR or SLIR.
As described, the variables and parameters involved in the quantitative models above are defined precisely in the previous literature. Obviously, an important motivation behind mathematical modeling of infectious disease spread is the evaluation of alternative control strategies. One approach to this is via optimal control theory. And it has become an especially important application with limited resources. The optimal control problem proposed by Neilan Rachael Miller and Lenhart Suzanne [21M.R. Neilan, and S. Lenhart, "An introduction to optimal control with an application in disease modeling", Am. Math. Soc., vol. 75, pp. 67-81, 2010.] designed to determine a vaccination strategy for minimizing a certain cost function. Furthermore, M. H. A. Biswas, L. T. Paiva and MdR DE Pinho [22M.H. Biswas, L.T. Paiva, and M.D. Pinho, "A SEIR model for control of infectious diseases with constraints", Math. Biosci. Eng., vol. 11, no. 4, pp. 761-784, 2014.
[http://dx.doi.org/10.3934/mbe.2014.11.761] ] considered the supply of vaccines was limited at each unit of time; so they introduced a mixed state-control constraint in control terms for further studying. In addition, the optimal control for information transmission is equally important. Chen Pinyu, Cheng Shamming and Chen Kwangcheng [23P.Y. Chen, S.M. Cheng, and K.C. Chen, "Optimal control of epidemic information dissemination over networks", IEEE Trans. Cybern., vol. 44, no. 12, pp. 2316-2328, 2014.
[http://dx.doi.org/10.1109/TCYB.2014.2306781] [PMID: 25415940] ] explored the optimal control policy for information dissemination with SIR model to minimize the accumulate network cost in reality. In contrast, Kundan Kandhway and Joy Kuri [24K. Kundan, and K. Joy, "How to run a campaign: Optimal control of SIS and SIR information epidemics", Appl. Math. Comput., vol. 231, pp. 79-92, 2014., 25K. Kandhway, and J. Kuri, "Optimal control of information epidemics modeled as Maki Thompson rumors", Commun. Nonlinear. Sci, vol. 19, no. 12, pp. 4135-4147, 2014.
[http://dx.doi.org/10.1016/j.cnsns.2014.04.022] ] formulated an optimal control of SIS and SIR information epidemics problem to maximum the transmission of information with fixed budget. Optimal control can be of help to test and compare different strategies of a certain problem. However, few works pay attention to the optimal control problem based on the model of SLIR to study network public opinion transmission till now.
So, in this article we propose the dynamic optimal control problem for the transmission of network public opinion. In addition, the isolation strategy is introduced to a control parameter which applied to a compartmental SLIR (susceptible, latently infected, infected and recovered) [22M.H. Biswas, L.T. Paiva, and M.D. Pinho, "A SEIR model for control of infectious diseases with constraints", Math. Biosci. Eng., vol. 11, no. 4, pp. 761-784, 2014.
[http://dx.doi.org/10.3934/mbe.2014.11.761] ]. This strategy concerns mainly about the control function among communicators, audience and media contents. Embedded the network’s “gatekeeper” is the main form of Isolation, it can strengthen the daily monitoring of network dissemination, those harmful content will be blocked or deleted at the first sign of trouble. Furthermore, an optimal objective based on the maximum social utility is established, namely, minimizing both the total outbreak size of public opinion and the relevant costs of isolation. To solve this problem, the Pontryagin’s Maximum Principle is utilized based on which it can deduce the optimized response measures. For instance, He Zaobo, Cai Zhipeng and Wang Xiaoming obtain the optimized control strategies that ensures a rumor can die out at the end of the time with lowest cost [26Z. He, Z. Cai, and X. Wang, "Modeling propagation dynamics and developing optimized countermeasures for rumor spreading in online social networks", In: 2015 IEEE 35th International Conference on, IEEE, 2015, pp. 205-214.
[http://dx.doi.org/10.1109/ICDCS.2015.29] ]. At Last, we appeal to numerical analysis technique to simulate the result, the effectiveness of the control methods in the network public opinion is verified.
This paper is organized as follows. Section 2 includes a short description of the SLIR model used in this paper. The optimal control problem with strategy isolation is presented in Section 3. And followed by Section 4 analyze the determination of the optimal solution. In Section 5, numerical simulations are carried out to allow better understanding of the dynamic behavior of the public opinion-spreading mechanism and the impact of the isolation control on network public opinion. The final section contains our conclusion.
2. THE SIMPLIFIED SLIR MODEL
In this paper, we apply to the simplified SLIR model with direct immune. This model divides people into four disjoint classes: susceptible, describing individuals who have not yet been aware of a particular network public opinion; latently infected, corresponding to individuals who are thinking about the network public opinion, but have not taken any action to it. infected, meaning individuals who transmit the public opinion through social interactions; and recovered, referring to individuals who have known the public opinion but choose not to spread it to others. Contacting from different parts makes the information dissemination and diffusion, thus changing the type of individuals. As Fig. (1 ):
):
The differential equation mathematical model is as follows:
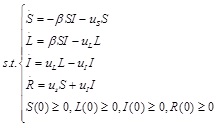 |
(1) |
The number of susceptible, latently infected, infected and recovered all at the moment t≥0 are denoted by S(t),L(t),I(t) and R(t) (In this paper, referred to S,L,I,R). The total population at time t is represented by N(t) = S(t) + L(t) + I(t) + R(t). To describe the public opinion transmission in a certain population, let uL be the rate at which the latently infected individuals transfer to infected, parameter uI is the proportionality constant of the rate of infected individuals recovering. These parameters are assumed to be constant in a finite horizon of interest. The rate of transmission is described by the number of contacts between susceptible and infected individuals. If β is the incidence coefficient of horizontal transmission, such rate is βS(t)I(t). Besides, some susceptible with profound knowledge (such as experts or scientists in relevant fields) will not be affected by the special public opinion, hence, these people directly recovered at a rate us, namely natural immunity [27G. Chen, H. Shen, T. Ye, G. Chen, and N. Kerr, "A kinetic model for the spread of rumor in emergencies", Discrete Dyn. Nat. Soc., pp. 1-8, 2013.]. And β, uL, uI, uS > 0
 |
Fig. (1) Structure of SLIR public opinion spreading process. |
3. FORMULATION OF THE OPTIMAL CONTROL PROBLEM
We consider a closed homogeneously mixed population in this article. There is no immigration, emigration, deaths, or births in the population. The nature of the network public opinion process is stochastic, because it is a probabilistic experiment that involves in time. So, the process is the stochastic network public opinion process.
Once public opinion announced, how to take timely and effective isolation strategy is our focus. Therefore, this paper introduced a control u to describe isolation strategy for public opinion 0 ≤ u ≤ umax ≤ 1 (If u = 0, then no isolation control is done and u = umax stands for maximum isolation control) and, we assume that isolation strategy is effective for reducing the density of infected. It can also be considered as increasing the transmission rate between infected and recovered. Taking all the above considerations into account that we can led to the following dynamical system:
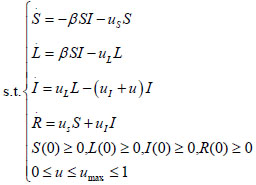 |
(2) |
The basic reproductive number for the system (2) is
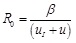 |
(3) |
Usually the public opinion will successfully invade when R 0 > 1 but will die out if R 0 < 1. Obviously, increasing the control u can effectively decrease the basic reproductive number.
From the control point of view, how to scientifically and reasonably select proper implementation scheme with the minimum cost and maximum interests has attracted our attention after the outbreak of public opinion. Therefore, our objective is to determine optimal isolation strategy that minimizes both the total outbreak size of public opinion and the relevant costs of isolation. We assume that application of the isolation control incurs a non-linear cost.
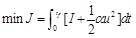 |
(4) |
Where tf is a fixed or free parameter (duration of the control interval).
Thus the optimal control problem can be formulates as:
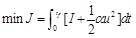
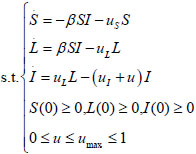 |
(5) |
The differential equation for the recovered compartment (R) is not presented here. This is due to the fact that the state variable R only appears in the corresponding differential equation, so it has no role in the overall system. Also, the number of recovered individuals at each instant t can be obtained from N(t) = S(t) + L(t) + I(t)+ R(t) .
4. OPTIMALITY SYSTEM
It is not difficult to see that the optimal control problem (5) admits an optimal solution. So, we only need to find the necessary conditions for the optimal control problem.
Denote Hamiltonian H (S, L, I, u, λS, λL, λI)
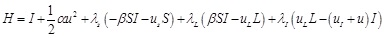
Where λS, λL and λI are co-state variables. By Pontryagin’s Maximum Principle, we have the following Theorem 4.1.
Theorem 4.1 If u is the optimal control of optimal control problem(5), S, L and I are the corresponding optimal paths, then there exist co-state variables, λS, λL and λI such that, besides the control system (2) is satisfied, the following conditions are satisfied:
(i) Co-state equations:
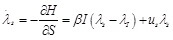 |
(6) |
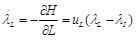 |
(7) |
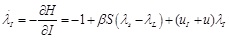 |
(8) |
Hamiltonian maximizing condition: At the interior points
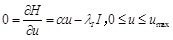 |
(9) |
(ii) Optimality conditions:
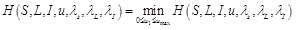
Hence the Hamiltonian maximizing condition leads to
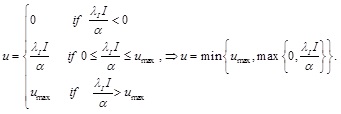 |
(10) |
(iii) Transversality conditions: From the transversality condition we get
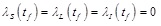 |
(11) |
The optimality system consists of the control system (2) coupled with the co-state equations (6)-(9) with the initial conditions and transversality conditions (11) together with the characterization of the optimal control (10).
5. OPTIMAL ISOLATION STRATEGY
In this section, we apply numerical analysis technique to simulate the result. The numerical results are obtained by problems of discretization (4), posing them as nonlinear constrained optimization problems and employing a gradient descent algorithm to arrive at an optimal solution. We study the shape of the susceptible, latently infected and infected with different control signal u over time. For
 , the parameter values used to generate the given figure can be found as follow. The control deadline is fixed at tf = 10, we take the maximum control effort for umax = 0.1 and umax = 0.9, respectively, cost weighting coefficient α = 2 , initial fraction of susceptible S(0) = 1000, latently infected, L(0) = 100 infected I(0) = 5. Other parameters will be taken as β = 0.04, uS = 0.005, uL = 0.05, uI = 0.002. The results are as follows:
, the parameter values used to generate the given figure can be found as follow. The control deadline is fixed at tf = 10, we take the maximum control effort for umax = 0.1 and umax = 0.9, respectively, cost weighting coefficient α = 2 , initial fraction of susceptible S(0) = 1000, latently infected, L(0) = 100 infected I(0) = 5. Other parameters will be taken as β = 0.04, uS = 0.005, uL = 0.05, uI = 0.002. The results are as follows:
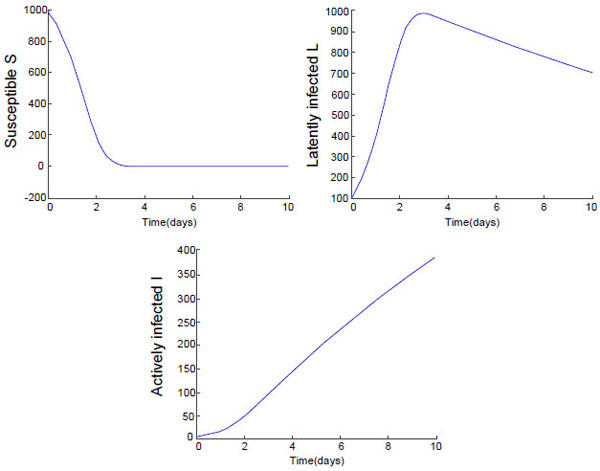 |
Fig. (2) There is no control (u = 0), the paths S (t), L (t), I (t) and the optimal control u (t) for 10 days. |
By the comparative analysis: 1) after the public opinion announced, the number of susceptible(S) is falling rapidly and infected number is on the rise. But as compared to the uncontrolled (Fig. 2 ), the infected number in Figs.(3
), the infected number in Figs.(3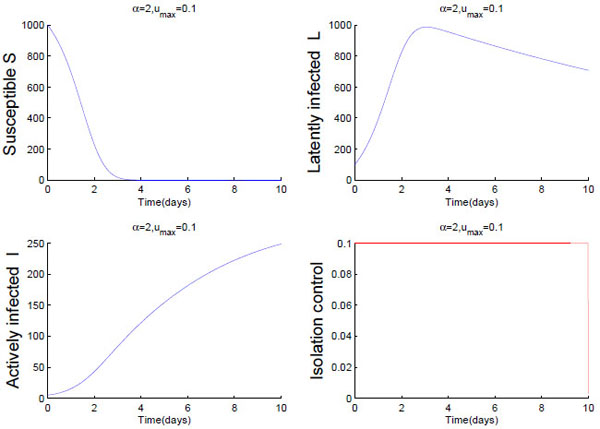 and 4
and 4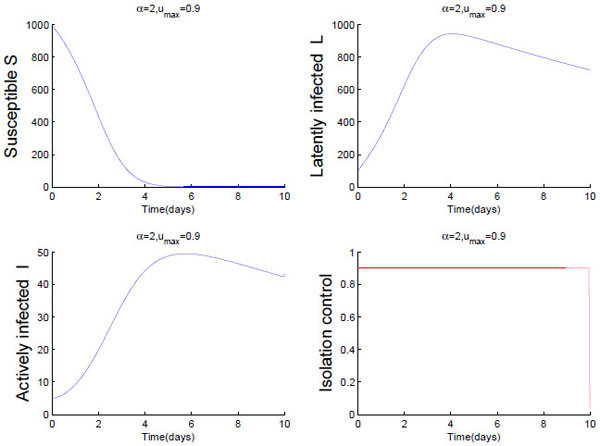 ) increase more gently and have a significantly lower final size in the control deadline. This suggests that the isolation control measures are valid to control the outbreak of public opinion. 2) Comparing Figs. (3
) increase more gently and have a significantly lower final size in the control deadline. This suggests that the isolation control measures are valid to control the outbreak of public opinion. 2) Comparing Figs. (3 and 4
and 4 ), we can find that the final control results are different with different isolation control. When the cost of control is larger, the number of infected in the simulation process represents descending trend in the stage of the second half (as shown in Fig. (4
), we can find that the final control results are different with different isolation control. When the cost of control is larger, the number of infected in the simulation process represents descending trend in the stage of the second half (as shown in Fig. (4 )). This means that the more fully the isolation resource is, the more obvious will be the effect. Hence the application of the optimal strategies leads to lower value of I(t) when compared to no control or a relatively small control is applied. 3) Besides, simulation also shows that the cost of the control has no obvious influence on the changing trend of susceptible. This once again suggests that in a closed system, to isolate infected people is the most effective way to control the transmission of the public opinion.
)). This means that the more fully the isolation resource is, the more obvious will be the effect. Hence the application of the optimal strategies leads to lower value of I(t) when compared to no control or a relatively small control is applied. 3) Besides, simulation also shows that the cost of the control has no obvious influence on the changing trend of susceptible. This once again suggests that in a closed system, to isolate infected people is the most effective way to control the transmission of the public opinion.
 |
Fig. (3) The maximum control umax=0.1, the paths S(t), L(t), I(t) and the optimal control u(t) for 10 days. |
 |
Fig. (4) The maximum control umax=0.9, the paths S(t), L(t), I(t) and the optimal control u(t) for 10 days. |
CONCLUSION
Public opinion is a double-edged sword which has a great effect on social life. In this paper, we have investigated isolation strategies for network public opinion spreading with SLIR model. It is indeed an effective way to make a control, based on both mathematical analysis and numerical results. So, after the outbreak of network public opinion, as long as the isolation strategy take, we will be able to effectively control the number of infected people. The more fully isolation resource is, the more obvious effect will be. This means that we have to abandon the cost factors for improving the control effect in reality. In other words, Progress comes at a high price. It can better explain that Intensive culling of poultry is an effective effort to contain an outbreak of the disease.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This research was supported by the Philosophy and Social Science major research project of Ministry of Education of China (No. 13JZD033), Natural Science Foundation of China (No. 71272209), and Humanity and Social Science Foundation of Ministry of Education of China (No. 12YJA630170) and the Natural Science Foundation of Hunan Province (No. 12JJ3081).
REFERENCES
| [1] | C. Su, J. Peng, and S. Li, "A survey on the mathematical modeling of internet public opinion research both at home and abroad", J. Intell., vol. 33, no. 10, pp. 14-20, 2014. |
| [2] | Q. Zhang, F. Liu, and Y. Huang, "A warning and urgent decision-making mechanism for uncertain network public sentiment emergency", J. Comput. (Taipei), vol. 8, no. 10, pp. 2640-2647, 2013. |
| [3] | X. Hu, Y. Zhang, and B. An, "The mechanism and influencing factors of herding effect of college students' network public opinion", Anthropologist., vol. 23, no. 1,2, pp. 226-230, 2016. |
| [4] | Y. Lan, and R. Zeng, "Research of emergency network public opinion on propagation model and warning phase", J. Intell., vol. 32, no. 5, pp. 16-19, 2013. |
| [5] | X. Zhao, and J. Wang, "Dynamical Model about Rumor Spreading with Medium. Discrete", Dyn. Nat. Soc., vol. 2013, pp. 1-9, 2013. [http://dx.doi.org/10.1155/2013/586867] |
| [6] | L. Zhao, X. Qiu, X. Wang, and J. Wang, "Rumor spreading model considering forgetting and remembering mechanisms in inhomogeneous networks", Physica A., vol. 392, no. 4, pp. 987-994, 2013. [http://dx.doi.org/10.1016/j.physa.2012.10.031] |
| [7] | L. Zhao, J. Wang, Y. Chen, Q. Wang, J. Cheng, and H. Cui, "SIHR rumor spreading model in social networks", Physica A., vol. 391, no. 7, pp. 2444-2453, 2012. [http://dx.doi.org/10.1016/j.physa.2011.12.008] |
| [8] | L. Zhao, Q. Wang, J. Cheng, D. Zhang, T. Ma, Y. Chen, and J. Wang, "The impact of authorities' media and rumor dissemination on the evolution of emergency", Physica A., vol. 391, no. 15, pp. 3978-3987, 2012. [http://dx.doi.org/10.1016/j.physa.2012.02.004] |
| [9] | Z. Zhao, Y. Liu, and K. Wang, "An analysis of rumor propagation based on propagation force", Physica A., vol. 443, pp. 263-271, 2016. [http://dx.doi.org/10.1016/j.physa.2015.09.060] |
| [10] | D. Liu, W. Wang, and H. Li, "Evolutionary mechanism and information supervision of public opinions in internet emergency", Procedia Comput. Sci., vol. 17, pp. 973-980, 2013. [http://dx.doi.org/10.1016/j.procs.2013.05.124] |
| [11] | X. Cheng, L. Zhu, Q. Zhu, and J. Wang, "The framework of network public opinion monitoring and analyzing system based on semantic content identification", J. Convergence Inf. Technol., vol. 5, no. 10, pp. 1-5, 2010. |
| [12] | K. Kyungmo, B. Young Min, and K. Narae, "Online news diffusion dynamics and public opinion formation: A case study of the controversy over judges' personal opinion expression on SNS in Korea", Soc. Sci. J., vol. 52, no. 2, pp. 205-216, 2015. [http://dx.doi.org/10.1016/j.soscij.2015.02.001] |
| [13] | W. Chai, and M. Cheng, "The research on the network public opinion risk assessment based on the CWAHP-entropy method", Int. J. Secur. Appl, vol. 10, no. 4, pp. 197-208, 2016. |
| [14] | S. Suo, and Y. Chen, "The dynamics of public opinion in complex networks", J. Artif. Soc. Soc. Simul., vol. 11, no. 4, p. 2, 2008. |
| [15] | U. Juliane, and B. Kristin, "Tracing public opinion online-an example of use for social network analysis in communication research", Procedia Soc. Behav. Sci., vol. 100, pp. 108-126, 2013. [http://dx.doi.org/10.1016/j.sbspro.2013.10.703] |
| [16] | Y. Ma, X. Shu, S. Shen, J. Song, G. Li, and Q. Liu, "Study on network public opinion dissemination and coping strategies in large fire disasters", Procedia Eng., vol. 71, pp. 616-621, 2014. [http://dx.doi.org/10.1016/j.proeng.2014.04.088] |
| [17] | J. Wu, S. Ni, and S. Shen, "Dynamics of public opinion under the influence of epidemic spreading", Int. J. Mod. Phys. C, vol. 27, no. 07, p. 1650079, 2016. [http://dx.doi.org/10.1142/S0129183116500790] |
| [18] | K. Kawachi, M. Seki, H. Yoshida, Y. Otake, K. Warashina, and H. Ueda, "A rumor transmission model with various contact interactions", J. Theor. Biol., vol. 253, no. 1, pp. 55-60, 2008. [http://dx.doi.org/10.1016/j.jtbi.2007.11.024] [PMID: 18179802] |
| [19] | G. R, L. David, T. A, "Information Diffusion Through Blogspace", In: Proceedings of the 13th international conference on World Wide Web, ACM, 2004, pp. 491-501. |
| [20] | B. Chen, L. Yu, J. Liu, and W. Chu, "Dissemination and control model of internet public opinion in the ubiquitous media environments", Xitong Gongcheng Lilum yu Shijian, vol. 31, no. 11, pp. 2140-2150, 2011. |
| [21] | M.R. Neilan, and S. Lenhart, "An introduction to optimal control with an application in disease modeling", Am. Math. Soc., vol. 75, pp. 67-81, 2010. |
| [22] | M.H. Biswas, L.T. Paiva, and M.D. Pinho, "A SEIR model for control of infectious diseases with constraints", Math. Biosci. Eng., vol. 11, no. 4, pp. 761-784, 2014. [http://dx.doi.org/10.3934/mbe.2014.11.761] |
| [23] | P.Y. Chen, S.M. Cheng, and K.C. Chen, "Optimal control of epidemic information dissemination over networks", IEEE Trans. Cybern., vol. 44, no. 12, pp. 2316-2328, 2014. [http://dx.doi.org/10.1109/TCYB.2014.2306781] [PMID: 25415940] |
| [24] | K. Kundan, and K. Joy, "How to run a campaign: Optimal control of SIS and SIR information epidemics", Appl. Math. Comput., vol. 231, pp. 79-92, 2014. |
| [25] | K. Kandhway, and J. Kuri, "Optimal control of information epidemics modeled as Maki Thompson rumors", Commun. Nonlinear. Sci, vol. 19, no. 12, pp. 4135-4147, 2014. [http://dx.doi.org/10.1016/j.cnsns.2014.04.022] |
| [26] | Z. He, Z. Cai, and X. Wang, "Modeling propagation dynamics and developing optimized countermeasures for rumor spreading in online social networks", In: 2015 IEEE 35th International Conference on, IEEE, 2015, pp. 205-214. [http://dx.doi.org/10.1109/ICDCS.2015.29] |
| [27] | G. Chen, H. Shen, T. Ye, G. Chen, and N. Kerr, "A kinetic model for the spread of rumor in emergencies", Discrete Dyn. Nat. Soc., pp. 1-8, 2013. |



