- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Cybernetics & Systemics Journal
(Discontinued)
ISSN: 1874-110X ― Volume 12, 2018
Decision-making Method for Clay-brick Selection Based on Subtraction Operational Aggregation Operators of Intuitionistic Fuzzy Values
Zhikang Lu, Jun Ye*
Abstract
The subtraction operation of intuitionistic fuzzy sets (IFSs) has been scarcely used for practical applications since it was introduced. Therefore, it is necessary to propose an aggregation operator based on the subtraction operation of IFSs for engineering applications. Then, clay-brick selection is an important decision-making problem for better building construction. To handle the decision-making problem based on the subtraction operation of IFSs in an intuitionistic fuzzy environment, this paper firstly introduces an intuitionistic fuzzy subtraction operational weighted arithmetic averaging (IFSOWAA) operator and investigates its properties. Then, we propose the IFSOWAA operator-based decision-making method as a supplement for existing decision-making methods under an intuitionistic fuzzy environment. Finally, an actual example about a clay-brick selection problem is provided to show the applicability and effectiveness of the proposed method.
Article Information
Identifiers and Pagination:
Year: 2016Volume: 10
First Page: 283
Last Page: 291
Publisher Id: TOCSJ-10-283
DOI: 10.2174/1874110X01610010283
Article History:
Received Date: 08/08/2016Revision Received Date: 25/09/2016
Acceptance Date: 31/10/2016
Electronic publication date: 30/12/2016
Collection year: 2016
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
* Address correspondence to this author at the Department of Electrical and Information Engineering, Shaoxing University, 508 Huancheng West Road, Shaoxing, Zhejiang Province 312000, P.R. China; Tel: +86-575-88327323; E-mail: yehjun@aliyun.com
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 08-08-2016 |
Original Manuscript | Decision-making Method for Clay-brick Selection Based on Subtraction Operational Aggregation Operators of Intuitionistic Fuzzy Values | |
1. INTRODUCTION
Multiple attribute decision-making problems are usually to find the most satisfactory alternative from all the feasible alternatives. Owing to the fuzziness of human thinking and cognition about complex decision-making problems, it is difficult to express the attribute values by crisp numbers. Then, a fuzzy set introduced by Zadeh [1L.A. Zadeh, "Fuzzy sets", Inf. Control, vol. 8, pp. 338-356, 1965.
[http://dx.doi.org/10.1016/S0019-9958(65)90241-X] ] can express fuzzy information in real world. After that, Atanassov [2K.T. Atanassov, "Intuitionistic fuzzy set", Fuzzy Sets Syst., vol. 20, pp. 87-96, 1986.
[http://dx.doi.org/10.1016/S0165-0114(86)80034-3] ] considered the non-membership degree and presented an intuitionistic fuzzy set (IFS) as a generalization of the fuzzy set. IFS is composed of a membership degree and a non-membership degree to describe vague and incomplete information. Therefore, IFS is a very useful tool for dealing with fuzziness and uncertainty in decision-making problems. Many methods have been developed to solve the complex multiple attribute decision-making problems with the IFS information [3D.F. Li, "Some measures of dissimilarity in intuitionistic fuzzy structures", J. Comput. Syst. Sci., vol. 68, pp. 115-122, 2004.
[http://dx.doi.org/10.1016/j.jcss.2003.07.006] -26H. Garg, "Generalized intuitionistic fuzzy interactive geometric interaction operators using Einstein t-norm and t-conorm and their application to decision making", Comp. Indus. Engi., vol. 101, pp. 53-69, 2016.
[http://dx.doi.org/10.1016/j.cie.2016.08.017] ]. As a supplement of basic operational laws over IFSs, Atanassov and Riecan [27K.T. Atanassov, and B. Riecan, "On two operations over intuitionistic fuzzy sets", J. Appl. Math. Stat. Info, vol. 2, pp. 145-148, 2006.] and Chen [28T.Y. Chen, "Remarks on the subtraction and division operations over intuitionistic fuzzy sets and interval-valued fuzzy sets", Int. J. Fuzzy Syst., vol. 9, no. 3, pp. 169-172, 2007.] introduced the subtraction and division operations over IFSs. However, the subtraction and division operations over IFSs are scarcely applied in science and engineering fields since they were presented. Therefore, it is necessary to propose some aggregation operators based on the subtraction and division operations of IFSs for engineering applications.
Clay-brick selection is an important decision-making problem for better building construction. To construct a building, a traditional selection method for clay-bricks provided from various brick fields is to select clay-bricks roughly based on their color, size, and total cost, without considering other quality factors of clay-bricks. In this case, the building construction may produce some dangerous problems regarding low quality clay-bricks. Therefore, it is necessary to formulate a scientific selection method. In order to select the most suitable brick to construct a building, we have to consider the solidity, color, size and shape, strength, cost of brick etc. as their evaluation indices (attributes) [29K. Mondal, and S. Pramanik, "Intuitionistic fuzzy multi-criteria group decision making approach to quality clay-brick selection problem based on grey relational analysis", J. Appl. Quant. Methods, vol. 9, no. 2, pp. 35-50, 2014., 30K. Mondal, and S. Pramanik, "Neutrosophic decision making model for clay-brick selection in construction field based on grey relational analysis", Neutrosophic Sets Syst., vol. 9, pp. 64-71, 2015.]. Hence, some researchers have proposed decision-making methods for clay-brick selection problems under intuitionistic fuzzy and single-valued neutrosophic environments [29K. Mondal, and S. Pramanik, "Intuitionistic fuzzy multi-criteria group decision making approach to quality clay-brick selection problem based on grey relational analysis", J. Appl. Quant. Methods, vol. 9, no. 2, pp. 35-50, 2014., 30K. Mondal, and S. Pramanik, "Neutrosophic decision making model for clay-brick selection in construction field based on grey relational analysis", Neutrosophic Sets Syst., vol. 9, pp. 64-71, 2015.].
Since existing various intuitionistic fuzzy aggregation operators cannot handle the information aggregation of the intuitionistic fuzzy subtraction operation and existing subtraction operation of intuitionistic fuzzy values (IFVs), which are basic elements in IFSs, lacks the practical applications, this paper presents an intuitionistic fuzzy subtraction operational weighted arithmetic averaging (IFSOWAA) operator and its decision-making method as a supplement of existing decision-making methods, and then applies the IFSOWAA operator-based decision-making method to the decision-making problem of clay-brick selection under an intuitionistic fuzzy environment.
The remainder of this paper is structured as follows. Section 2 reviews some basic knowledge of IFSs and operations of IFVs. Section 3 proposes an IFSOWAA operator based on the subtraction operation of IFVs and investigates its properties. In Section 4, a multiple attribute decision-making method is developed based on the IFSOWAA operator. In Section 5, an actual example about a clay-brick selection problem is provided to show the applicability and effectiveness of the proposed method. Some conclusions and future research are discussed in Section 6.
2. SOME BASIC KNOWLEDGE OF IFSS AND OPERATIONS OF IFVS
Atanassov [2K.T. Atanassov, "Intuitionistic fuzzy set", Fuzzy Sets Syst., vol. 20, pp. 87-96, 1986.
[http://dx.doi.org/10.1016/S0165-0114(86)80034-3] ] extended fuzzy set to IFS and introduced its definition.
Definition 1 [2K.T. Atanassov, "Intuitionistic fuzzy set", Fuzzy Sets Syst., vol. 20, pp. 87-96, 1986.
[http://dx.doi.org/10.1016/S0165-0114(86)80034-3] ]. Let X be a universal of discourse. An IFS N in X is characterized by a membership function uN(x), a non-membership function vN(x), where the values of the two functions uN(x) and vN(x) are real numbers in the interval [0, 1], such that uN(x)
 [0, 1] and vN(x)
[0, 1] and vN(x)
 [0, 1] and 0 ≤ uN(x) + vN(x) ≤ 1. Thus, an IFS N is denoted by the mathematical symbol:
[0, 1] and 0 ≤ uN(x) + vN(x) ≤ 1. Thus, an IFS N is denoted by the mathematical symbol:
Then,
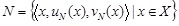 |
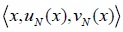 in an IFS N is denoted by a = <ua, va> for short, which is called IFV [4Z.S. Xu, and R.R. Yager, "Some geometric aggregation operators based on intuitionistic fuzzy sets", Int. J. Gen. Syst., vol. 35, pp. 417-433, 2006.
in an IFS N is denoted by a = <ua, va> for short, which is called IFV [4Z.S. Xu, and R.R. Yager, "Some geometric aggregation operators based on intuitionistic fuzzy sets", Int. J. Gen. Syst., vol. 35, pp. 417-433, 2006.[http://dx.doi.org/10.1080/03081070600574353] ].
Let
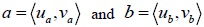 be two IFVs, then there are the following relations [2K.T. Atanassov, "Intuitionistic fuzzy set", Fuzzy Sets Syst., vol. 20, pp. 87-96, 1986.
be two IFVs, then there are the following relations [2K.T. Atanassov, "Intuitionistic fuzzy set", Fuzzy Sets Syst., vol. 20, pp. 87-96, 1986.
[http://dx.doi.org/10.1016/S0165-0114(86)80034-3] ]:
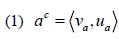 (complement of a);
(complement of a);
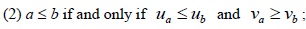

After that, the basic operational laws of the two IFVs
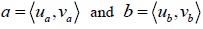 are introduced as follows [7Z.S. Xu, "Intuitionistic fuzzy aggregation operators", IEEE Trans. Fuzzy Syst., vol. 15, pp. 1179-1187, 2007.
are introduced as follows [7Z.S. Xu, "Intuitionistic fuzzy aggregation operators", IEEE Trans. Fuzzy Syst., vol. 15, pp. 1179-1187, 2007.
[http://dx.doi.org/10.1109/TFUZZ.2006.890678] ]:
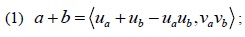
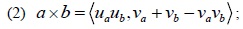
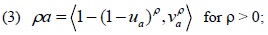
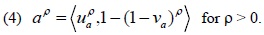
For any IFV a = <ua, va> its score and accuracy functions [31S.M. Chen, and J.M. Tan, "Handling multi-criteria fuzzy decision making problems based on vague set theory", Fuzzy Sets Syst., vol. 67, pp. 163-172, 1994.
[http://dx.doi.org/10.1016/0165-0114(94)90084-1] , 32D.H. Hong, and C.H. Choi, "Multi-criteria fuzzy decision-making problems based on vague set theory", Fuzzy Sets Syst., vol. 114, pp. 103-113, 2000.
[http://dx.doi.org/10.1016/S0165-0114(98)00271-1] ] are introduced, respectively, as follows:
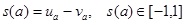 |
(1) |
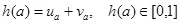 |
(2) |
Definition 2 [4Z.S. Xu, and R.R. Yager, "Some geometric aggregation operators based on intuitionistic fuzzy sets", Int. J. Gen. Syst., vol. 35, pp. 417-433, 2006.
[http://dx.doi.org/10.1080/03081070600574353] , 7Z.S. Xu, "Intuitionistic fuzzy aggregation operators", IEEE Trans. Fuzzy Syst., vol. 15, pp. 1179-1187, 2007.
[http://dx.doi.org/10.1109/TFUZZ.2006.890678] ]. Let
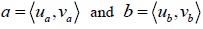 be two IFVs, then according to the score values of s(a) and s(b) and the accuracy degrees of h(a) and h(b), there are the following relations:
be two IFVs, then according to the score values of s(a) and s(b) and the accuracy degrees of h(a) and h(b), there are the following relations:
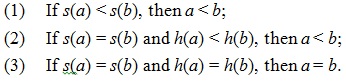
Let
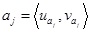 (j = 1, 2,..., n) be a collection of IFVs, then the following intuitionistic fuzzy weighted arithmetic averaging (IFWAA) operator [7Z.S. Xu, "Intuitionistic fuzzy aggregation operators", IEEE Trans. Fuzzy Syst., vol. 15, pp. 1179-1187, 2007.
(j = 1, 2,..., n) be a collection of IFVs, then the following intuitionistic fuzzy weighted arithmetic averaging (IFWAA) operator [7Z.S. Xu, "Intuitionistic fuzzy aggregation operators", IEEE Trans. Fuzzy Syst., vol. 15, pp. 1179-1187, 2007.
[http://dx.doi.org/10.1109/TFUZZ.2006.890678] ] are introduced as follows:
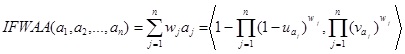 |
(3) |
where wj (j = 1, 2, …, n) is the weight of aj (j = 1, 2, …, n) with
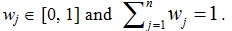
3. SUBTRACTION OPERATIONAL WEIGHTED AGGREGATION OPERATOR OF IFVS
Based on the subtraction operation over IFVs, this section proposes its aggregation operator.
Definition 3. Let a = <ua, va> and b = <ub, vb> be two IFVs, then the subtraction operation of the IFVs a and b is defined as follows [27K.T. Atanassov, and B. Riecan, "On two operations over intuitionistic fuzzy sets", J. Appl. Math. Stat. Info, vol. 2, pp. 145-148, 2006., 28T.Y. Chen, "Remarks on the subtraction and division operations over intuitionistic fuzzy sets and interval-valued fuzzy sets", Int. J. Fuzzy Syst., vol. 9, no. 3, pp. 169-172, 2007.]:
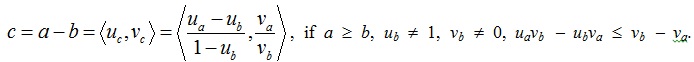 |
(4) |
Based on the basic operational laws of IFVs, we introduce the following theorem:
Theorem 1. Let a = <ua, va> and b = <ub, vb> be two IFVs, ρ > 0. Then, there are the following operational laws of (a − b):
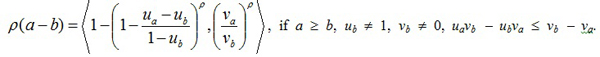 |
(5) |
 |
(6) |
Obviously, Eqs. (5) and (6) are true according to the basic operational laws of IFVs.
Let
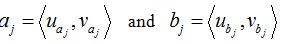 (j = 1,2,..n) be two collections of IFVs and
(j = 1,2,..n) be two collections of IFVs and
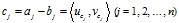 be a collection of cj. Based on the intuitionistic fuzzy weighted arithmetic averaging aggregation operator of Eq. (3) and Theorem 1, if these conditions aj ≤ bj, ubj≠1, vbj≠0, uajvbj-ubjvaj ≤ vbj-vaj are satisfied, we can introduce the intuitionistic fuzzy subtraction operational weighted arithmetic averaging (IFSOWAA) operator:
be a collection of cj. Based on the intuitionistic fuzzy weighted arithmetic averaging aggregation operator of Eq. (3) and Theorem 1, if these conditions aj ≤ bj, ubj≠1, vbj≠0, uajvbj-ubjvaj ≤ vbj-vaj are satisfied, we can introduce the intuitionistic fuzzy subtraction operational weighted arithmetic averaging (IFSOWAA) operator:
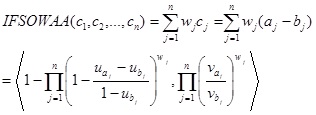 |
(7) |
where wj (j = 1, 2, …, n) is the weight of cj = aj – bj (j = 1, 2, …, n) with
 Especially when wj = 1/n (j = 1,2,...,n) the IFSOWAA operator is degenerated to the intuitionistic fuzzy subtraction operational arithmetic averaging operator.
Especially when wj = 1/n (j = 1,2,...,n) the IFSOWAA operator is degenerated to the intuitionistic fuzzy subtraction operational arithmetic averaging operator.
Based on the properties of the IFWAA operator [7Z.S. Xu, "Intuitionistic fuzzy aggregation operators", IEEE Trans. Fuzzy Syst., vol. 15, pp. 1179-1187, 2007.
[http://dx.doi.org/10.1109/TFUZZ.2006.890678] ], it is obvious that the IFSOWAA operator also satisfy the properties of idempotency, boundedness and monotonicity:
(1) Idempotency:
If cj = c for j = 1, 2, . . ., n, then there is
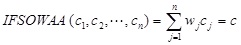
(2) Boundedness:
If Cmin = min(C1, C2,...,Cn) and Cmax = max(C1, C2,...,Cn) for j = 1, 2,.., n, then there is
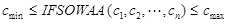 .
.
(3) Monotonicity:
If cj ≤ cj* for j = 1, 2, . . ., n, then there is

4. DECISION-MAKING METHOD BASED ON THE IFSOWAA OPERATOR
In this section, we present a handling method for multiple attribute decision-making problems based on the IFSOWAA operator.
In a multiple attribute decision-making problem, we suppose that T = {T1, T2, …, Tm} be a set of alternatives and M = {M1, M2, …, Mn} be a set of attributes. The weight of each attribute Mj (j = 1, 2, …, n) is considered as wj, satisfying
 . Then, the characteristic of each alternative Ti (i = 1, 2, …, m) with respect to each attribute Mj (j = 1, 2, …, n) is evaluated by the decision-maker and the evaluation values are expressed by the IFV
. Then, the characteristic of each alternative Ti (i = 1, 2, …, m) with respect to each attribute Mj (j = 1, 2, …, n) is evaluated by the decision-maker and the evaluation values are expressed by the IFV
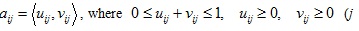 = 1, 2,…, n; i = 1, 2,…, m), and then
= 1, 2,…, n; i = 1, 2,…, m), and then
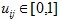 indicates the degree that the alternative Ti is satisfactory to the attribute Mj and
indicates the degree that the alternative Ti is satisfactory to the attribute Mj and
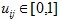 indicates the degree that the alternative Ti is unsatisfactory to the attribute Mj. Therefore, we can establish an IFV decision matrix D = (aij)m×n.
indicates the degree that the alternative Ti is unsatisfactory to the attribute Mj. Therefore, we can establish an IFV decision matrix D = (aij)m×n.
As for the multiple attribute decision-making problem, we propose a decision-making method, which is described by the following steps:
Step 1. Based on the IFV decision matrix D = (aij)m×n, the j-th IFV positive ideal solution can be determined
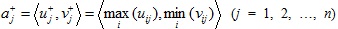 and the j-th IFV negative ideal solution can be determined by
and the j-th IFV negative ideal solution can be determined by
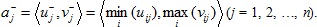 . Thus they are constructed as both the ideal alternative M+ = {a1+, a2+,...,an+} and the non-ideal alternative M- = {a1-, a2-,...,an+}.
. Thus they are constructed as both the ideal alternative M+ = {a1+, a2+,...,an+} and the non-ideal alternative M- = {a1-, a2-,...,an+}.
Step 2. According to Eq. (7), two collective values Ci+ and Ci- (i = 1, 2, …, m) for each alternative Ti (i = 1, 2, …, m) can be calculated by the following IFSOWAA operators:
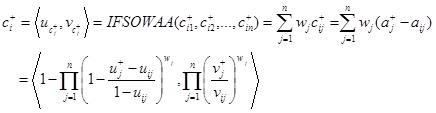 |
(8) |
 |
(9) |
Step 3. We calculate the values of H(Ci+) and H(Ci-) (i = 1, 2, …, m) by the hybrid functions of the score and accuracy functions with a real parameter 0 ≤ ρ ≤ 1:
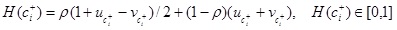 |
(10) |
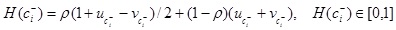 |
(11) |
Step 4. The relative closeness degree of each alternative with respect to the ideal alternative (i = 1, 2, …, m) is calculated by:
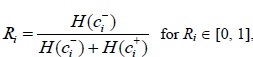 |
(12) |
Obviously, the larger value of Ri reveals that the alternative is closer to the ideal alternative and farther from the non-ideal alternative simultaneously. Therefore, all the alternatives can be ranked by the values of Ri (i = 1, 2, …, m) in a descending order. The alternative with the largest value is the best choice.
Step 5. End.
5. ACTUAL EXAMPLE OF CLAY-BRICK SELECTION
In this section, an actual example about a clay-brick selection problem (adapted from [30K. Mondal, and S. Pramanik, "Neutrosophic decision making model for clay-brick selection in construction field based on grey relational analysis", Neutrosophic Sets Syst., vol. 9, pp. 64-71, 2015.]) in a construction company is provided under an intuitionistic fuzzy environment to demonstrate the applicability and effectiveness of the IFSOWAA operator-based multiple attribute decision-making method in realistic scenarios.
For constructing a building, a construction company needs to select the four types of clay-bricks, which are provided from various brick fields, as a set of alternatives T = {T1, T2, T3, T4}. To select the most suitable brick for constructing a building, it is necessary to evaluate the four types of clay-bricks by the six attributes of clay-bricks obtained from experts’ opinions [30K. Mondal, and S. Pramanik, "Neutrosophic decision making model for clay-brick selection in construction field based on grey relational analysis", Neutrosophic Sets Syst., vol. 9, pp. 64-71, 2015.]: (1) M1 is solidity, (2) M2 is color, (3) M3 is size and shape, (4) M4 is strength, (5) M5 is cost, (6) M6 is carrying cost. The weight vector of the six attributes is given by w = (0.275, 0.175, 0.2, 0.1, 0.05, 0.2). Experts or decision makers are required to evaluate the four possible alternatives under the above six attributes by suitability judgments.
To indicate the evaluation of an alternative Ti (i =1, 2, 3, 4) with respect to an attribute Mj (j =1, 2, …, 6), it can be obtained from the questionnaire or score law of domain experts. For example, when we ask the opinion of an expert about an alternative T1 with respect to an attribute M1, he/she may say that the possibility in which the statement is suitable is 0.7 and the statement is unsuitable is 0.2. By the intuitionistic fuzzy notation, it can be expressed as
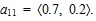 Similarly, when the four possible alternatives with respect to the above six attributes are evaluated by the expert, based on [30K. Mondal, and S. Pramanik, "Neutrosophic decision making model for clay-brick selection in construction field based on grey relational analysis", Neutrosophic Sets Syst., vol. 9, pp. 64-71, 2015.] we can construct the following IFV decision matrix:
Similarly, when the four possible alternatives with respect to the above six attributes are evaluated by the expert, based on [30K. Mondal, and S. Pramanik, "Neutrosophic decision making model for clay-brick selection in construction field based on grey relational analysis", Neutrosophic Sets Syst., vol. 9, pp. 64-71, 2015.] we can construct the following IFV decision matrix:
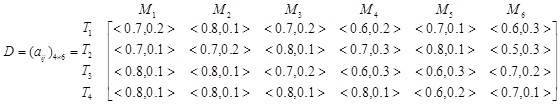 |
In the decision-making problem of the clay-brick selection, the proposed decision-making method can be applied and the decision steps are described as follows:
Step 1. By
 3, 4;j = 1,2,...,6) we can determine both the IFV positive ideal solutions in the ideal alternative and the IFV negative ideal solutions in the non-ideal alternative, respectively, as follows:
3, 4;j = 1,2,...,6) we can determine both the IFV positive ideal solutions in the ideal alternative and the IFV negative ideal solutions in the non-ideal alternative, respectively, as follows:

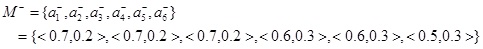
Step 2. By using Eqs. (8) and (9), we can obtain the two collective values ci+ and ci- (i = 1, 2, 3, 4) for each alternative Ti (i = 1, 2, 3, 4):
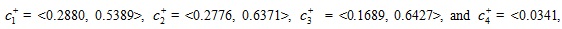 ,0.9659>;
,0.9659>;
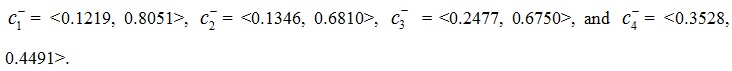
Step 3. By applying Eqs. (10) and (11) and taking ρ= 0.5, we calculate the values of H (Ci+) and H (Ci-) (i = 1, 2, 3, 4):
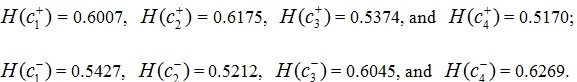 |
Step 4. By using Eq. (12), we calculate the relative closeness degrees of each alternative with respect to the ideal alternative for Ri (i = 1, 2, 3, 4):
R1 = 0.4746, R2 = 0.4577, R3 = 0.5294, and R4 = 0.5480.
Since the ranking order of the relative closeness degrees is R4 > R3 > R1 > R2, the ranking order of the four alternatives is
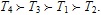 . Hence, the best alternative is T4.
. Hence, the best alternative is T4.
By a comparison with the decision-making method in [30K. Mondal, and S. Pramanik, "Neutrosophic decision making model for clay-brick selection in construction field based on grey relational analysis", Neutrosophic Sets Syst., vol. 9, pp. 64-71, 2015.], although the ranking orders are different, the best alternative is the same result as in [30K. Mondal, and S. Pramanik, "Neutrosophic decision making model for clay-brick selection in construction field based on grey relational analysis", Neutrosophic Sets Syst., vol. 9, pp. 64-71, 2015.]. Hence, the decision result of the decision-making method proposed in this paper is suitable. It is obvious that the main advantage of the proposed approach is simpler and more convenient than existing related method in [30K. Mondal, and S. Pramanik, "Neutrosophic decision making model for clay-brick selection in construction field based on grey relational analysis", Neutrosophic Sets Syst., vol. 9, pp. 64-71, 2015.].
To further demonstrate the effectiveness and rationality of the proposed method in this paper, we compare the proposed method with the conventional method based on the IFWAA operator introduced in [7Z.S. Xu, "Intuitionistic fuzzy aggregation operators", IEEE Trans. Fuzzy Syst., vol. 15, pp. 1179-1187, 2007.
[http://dx.doi.org/10.1109/TFUZZ.2006.890678] ] and the score and accuracy functions. By directly using the IFWAA operator of Eq. (3), we can obtain all the collective values of ai = IFWAA (ai1, ai2, ai3, ai4, ai5, ai6) (i = 1, 2, 3, 4) for each alternative Ti (i = 1, 2, 3, 4):
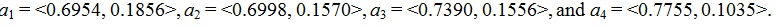 |
By applying Eq. (1), we calculate the score values of s(ai) for each alternative Ti (i = 1, 2, 3, 4):
s(a1) = 0.5098, s(a2) = 0.5428, s(a3) = 0.5834, and s(a4) = 0.6719.
Since the ranking order of the score values is s(a4) > s(a3) > s(a2) > s(a1), the ranking order of the four alternatives is
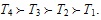 . Hence, the best alternative is T4.
. Hence, the best alternative is T4.
For the above two decision results with respect to the two decision-making methods based on the IFSOWAA and IFWAA operators, we can see that the two ranking orders of the alternatives only reveal difference between T1 and T2, while the ranking order
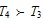 and the best alternative T4 are identical. Therefore, the decision-making method proposed in this paper is effective and provides a useful supplement for existing decision-making methods under an IFV environment.
and the best alternative T4 are identical. Therefore, the decision-making method proposed in this paper is effective and provides a useful supplement for existing decision-making methods under an IFV environment.
CONCLUSION
To use the subtraction operation of IFVs for practical applications, this paper presented the IFSOWAA operator for IFVs. Next, we developed a multiple attribute decision-making method based on the IFSOWAA operator. Finally, an actual example about a clay-brick selection problem was provided to demonstrate the applicability and effectiveness of the developed method. However, the proposed decision-making method provides both a useful supplement and another new way for existing decision-making methods under an IFV environment. In the future work, the developed method will be further extended to other fields, such as pattern recognition, image processing and clustering analysis.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
Decleared none.
REFERENCES
| [1] | L.A. Zadeh, "Fuzzy sets", Inf. Control, vol. 8, pp. 338-356, 1965. [http://dx.doi.org/10.1016/S0019-9958(65)90241-X] |
| [2] | K.T. Atanassov, "Intuitionistic fuzzy set", Fuzzy Sets Syst., vol. 20, pp. 87-96, 1986. [http://dx.doi.org/10.1016/S0165-0114(86)80034-3] |
| [3] | D.F. Li, "Some measures of dissimilarity in intuitionistic fuzzy structures", J. Comput. Syst. Sci., vol. 68, pp. 115-122, 2004. [http://dx.doi.org/10.1016/j.jcss.2003.07.006] |
| [4] | Z.S. Xu, and R.R. Yager, "Some geometric aggregation operators based on intuitionistic fuzzy sets", Int. J. Gen. Syst., vol. 35, pp. 417-433, 2006. [http://dx.doi.org/10.1080/03081070600574353] |
| [5] | L. Lin, X.H. Yuan, and Z.Q. Xia, "Multicriteria fuzzy decision-making methods based on intuitionistic fuzzy sets", J. Comput. Syst. Sci., vol. 73, pp. 84-88, 2007. [http://dx.doi.org/10.1016/j.jcss.2006.03.004] |
| [6] | H.W. Liu, and G.J. Wang, "Multi-attribute decision-making methods based on intuitionistic fuzzy sets", Eur. J. Oper. Res., vol. 179, pp. 220-233, 2007. [http://dx.doi.org/10.1016/j.ejor.2006.04.009] |
| [7] | Z.S. Xu, "Intuitionistic fuzzy aggregation operators", IEEE Trans. Fuzzy Syst., vol. 15, pp. 1179-1187, 2007. [http://dx.doi.org/10.1109/TFUZZ.2006.890678] |
| [8] | Z.S. Xu, "Some similarity measures of intuitionistic fuzzy sets and their applications to multiple attribute decision making", Fuzzy Optim. Decis. Making, vol. 6, pp. 109-121, 2007. [http://dx.doi.org/10.1007/s10700-007-9004-z] |
| [9] | D.F. Li, "Extension of the LINMAP for multi-attribute decision making under Atanassov’s intuitionistic fuzzy environment", Fuzzy Optim. Decis. Making, vol. 7, pp. 7-34, 2008. [http://dx.doi.org/10.1007/s10700-007-9022-x] |
| [10] | Z.S. Xu, and R.R. Yager, "Dynamic intuitionistic fuzzy multi-attribute decision making", Int. J. Approx. Reason., vol. 48, pp. 246-262, 2008. [http://dx.doi.org/10.1016/j.ijar.2007.08.008] |
| [11] | G.W. Wei, "Maximizing deviation method for multiple attribute decision making in intuitionistic fuzzy setting", Knowl. Base. Syst., vol. 21, pp. 833-836, 2008. [http://dx.doi.org/10.1016/j.knosys.2008.03.038] |
| [12] | Z.W. Gong, L.S. Li, F.X. Zhou, and T.X. Yai, "Goal programming approaches to obtain the priority vectors from the intuitionistic fuzzy preference relations", Comp. Indus. Engi, vol. 57, pp. 1187-1193, 2009. [http://dx.doi.org/10.1016/j.cie.2009.05.007] |
| [13] | G.W. Wei, "GRA method for multiple attribute decision making with incomplete weight information in intuitionistic fuzzy setting", Knowl. Base. Syst., vol. 23, pp. 243-247, 2010. [http://dx.doi.org/10.1016/j.knosys.2010.01.003] |
| [14] | G.W. Wei, "Some induced geometric aggregation operators with intuitionistic fuzzy information and their application to group decision making’", Appl. Soft Comput., vol. 10, pp. 423-431, 2010. [http://dx.doi.org/10.1016/j.asoc.2009.08.009] |
| [15] | Z.S. Xu, and H. Hu, "Projection models for intuitionistic fuzzy multiple attribute decision making", Int. J. Inf. Technol. Decis. Mak, vol. 9, no. 2, pp. 267-280, 2010. [http://dx.doi.org/10.1142/S0219622010003816] |
| [16] | J. Ye, "Fuzzy decision-making method based on the weighted correlation coefficient under intuitionistic fuzzy environment", Eur. J. Oper. Res., vol. 205, pp. 202-204, 2010. [http://dx.doi.org/10.1016/j.ejor.2010.01.019] |
| [17] | J. Ye, "Multiple attribute group decision-making methods with completely unknown weights in intuitionistic fuzzy setting and interval-valued intuitionistic fuzzy setting", Group Decis. Negot., vol. 22, no. 2, pp. 173-188, 2013. [http://dx.doi.org/10.1007/s10726-011-9255-5] |
| [18] | S.P. Wan, and D.F. Li, "Atanassov’s intuitionistic fuzzy programming method for heterogeneous multiattribute group decision making with Atanassov’s intuitionistic fuzzy truth degrees", IEEE Trans. Fuzzy Syst., vol. 22, no. 2, pp. 300-312, 2014. [http://dx.doi.org/10.1109/TFUZZ.2013.2253107] |
| [19] | S.P. Wan, F. Wang, L.L. Lin, and J.Y. Dong, "An intuitionistic fuzzy linear programming method for logistics outsourcing provider selection", Knowl. Base. Syst., vol. 82, pp. 80-94, 2015. [http://dx.doi.org/10.1016/j.knosys.2015.02.027] |
| [20] | J. Ye, "Similarity measures of intuitionistic fuzzy sets based on cosine function for the decision making of mechanical design schemes", J. Intell. Fuzzy Syst., vol. 30, pp. 151-158, 2016. [http://dx.doi.org/10.3233/IFS-151741] |
| [21] | S.P. Wan, F. Wang, and J.Y. Dong, "A novel group decision making method with intuitionistic fuzzy preference relations for RFID technology selection", Appl. Soft Comput., vol. 38, pp. 405-422, 2016. [http://dx.doi.org/10.1016/j.asoc.2015.09.039] |
| [22] | S.P. Wan, F. Wang, and J.Y. Dong, "A novel risk attitudinal ranking method for intuitionistic fuzzy values and application to MADM", Appl. Soft Comput., vol. 40, pp. 98-112, 2016. [http://dx.doi.org/10.1016/j.asoc.2015.11.022] |
| [23] | G.L. Xu, S.P. Wan, F. Wang, J.Y. Dong, and Y.F. Zeng, "Mathematical programming methods for consistency and consensus in group decision making with intuitionistic fuzzy preference relations", Knowl. Base. Syst., vol. 98, pp. 30-43, 2016. [http://dx.doi.org/10.1016/j.knosys.2015.12.007] |
| [24] | J. Xu, S.P. Wan, and J.Y. Dong, "Aggregating decision information into Atanassov's intuitionistic fuzzy numbers for heterogeneous multi-attribute group decision making", Appl. Soft Comput., vol. 41, pp. 331-351, 2016. [http://dx.doi.org/10.1016/j.asoc.2015.12.045] |
| [25] | H. Garg, "Some series of intuitionistic fuzzy interactive averaging aggregation operators", Springerplus, vol. 5, no. 1, p. 999, 2016. [http://dx.doi.org/10.1186/s40064-016-2591-9] [PMID: 27441128] |
| [26] | H. Garg, "Generalized intuitionistic fuzzy interactive geometric interaction operators using Einstein t-norm and t-conorm and their application to decision making", Comp. Indus. Engi., vol. 101, pp. 53-69, 2016. [http://dx.doi.org/10.1016/j.cie.2016.08.017] |
| [27] | K.T. Atanassov, and B. Riecan, "On two operations over intuitionistic fuzzy sets", J. Appl. Math. Stat. Info, vol. 2, pp. 145-148, 2006. |
| [28] | T.Y. Chen, "Remarks on the subtraction and division operations over intuitionistic fuzzy sets and interval-valued fuzzy sets", Int. J. Fuzzy Syst., vol. 9, no. 3, pp. 169-172, 2007. |
| [29] | K. Mondal, and S. Pramanik, "Intuitionistic fuzzy multi-criteria group decision making approach to quality clay-brick selection problem based on grey relational analysis", J. Appl. Quant. Methods, vol. 9, no. 2, pp. 35-50, 2014. |
| [30] | K. Mondal, and S. Pramanik, "Neutrosophic decision making model for clay-brick selection in construction field based on grey relational analysis", Neutrosophic Sets Syst., vol. 9, pp. 64-71, 2015. |
| [31] | S.M. Chen, and J.M. Tan, "Handling multi-criteria fuzzy decision making problems based on vague set theory", Fuzzy Sets Syst., vol. 67, pp. 163-172, 1994. [http://dx.doi.org/10.1016/0165-0114(94)90084-1] |
| [32] | D.H. Hong, and C.H. Choi, "Multi-criteria fuzzy decision-making problems based on vague set theory", Fuzzy Sets Syst., vol. 114, pp. 103-113, 2000. [http://dx.doi.org/10.1016/S0165-0114(98)00271-1] |



