- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Cybernetics & Systemics Journal
(Discontinued)
ISSN: 1874-110X ― Volume 12, 2018
Quantum Path-Integral qPATHINT Algorithm
Lester Ingber*
Abstract
Background:
A path-integral algorithm, PATHINT used previously for several systems, has been generalized from 1 dimension to N dimensions, and from classical to quantum systems into qPATHINT. Previous publications applied qPATHINT to two systems developed by the author, in neocortical interactions and financial options. Also, previous publications using classical PATHINT have developed a Statistical Mechanics of Neocortical Interactions (SMNI) that has been fitted to EEG data under attentional experimental paradigms. Classical PATHINT also has been published demonstrating development of Eurodollar options in industrial applications.
Objective:
A study is required to see if the qPATHINT algorithm can scale sufficiently to further develop real-world calculations in these two systems, requiring interactions between classical and quantum scales. A new algorithm also is needed to develop interactions between classical and quantum scales.
Method:
Both systems are developed using mathematical-physics methods of path integrals in quantum spaces. Supercomputer pilot studies using XSEDE.org resources tested various dimensions for their scaling limits. A simple modification of qPATHINT permits cloning code from 1 dimension to N dimensions. For the neuroscience study, tripartite neuron-astrocyte-neuron Ca-ion waves are propagated for 100’s of msec. For the financial options study, all traded Greeks are calculated for Eurodollar options in quantum-money spaces.
Results:
The mathematical-physics and computer parts of the study are successful for both systems. A 3-dimensional path-integral propagation of qPATHINT for both systems is within normal computational bounds on supercomputers. The neuroscience quantum path-integral also has a closed solution at arbitrary time that tests qPATHINT.
Conclusion:
Each of the two systems considered contribute insight into applications of qPATHINT to the other system, leading to new algorithms presenting time-dependent propagation of interacting quantum and classical scales. This can be achieved by propagating qPATHINT and PATHINT in synchronous time for the interacting systems, which is a future set of studies.
Article Information
Identifiers and Pagination:
Year: 2017Volume: 11
First Page: 119
Last Page: 133
Publisher Id: TOCSJ-11-119
DOI: 10.2174/1874110X01711010119
Article History:
Received Date: 10/11/2017Revision Received Date: 12/12/2017
Acceptance Date: 12/12/2017
Electronic publication date: 29/12/2017
Collection year: 2017
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: (https://creativecommons.org/licenses/by/4.0/legalcode). This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
* Address correspondence to this author at the Lester Ingber Research, Ashland, OR, USA; Tel: 15417081898; E-mail: ingber @ingber.com
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 10-11-2017 |
Original Manuscript | Quantum Path-Integral qPATHINT Algorithm | |
1. INTRODUCTION
Section 2 gives motivations for this proposed study. This includes published work with specific applications to neuroscience and to financial options.
Section 3 describes the math-physics methodology used for path-integral development, and its generic application to many physical systems. The algorithm to be used is based on that used in previous publications, PATHINT, a kernel type method particularly well suited for time-dependent and boundary-dependent systems, for which other Monte Carlo methods are not as useful. Specific equations are given to highlight this method; computational scaling conditions are shown to be highly dependent on the dimensionality of the given system. Scaling issues are discussed for different dimensions.
Section 4 describes the adaptation of the previous algorithm to quantum systems, defining the qPATHINT code within descriptions of two systems in neuroscience and financial options. Direct calculation of the propagation of the distribution or wave function in time-dependent scenarios is often required. Some other algorithms convert time-dependence to imaginary time to get real variables, but these suffer the problem of not having an audit trail back to the original real-time evolving wave function. Therefore, the PATHINT C code of about 7500 lines of code was rewritten for the GCC C-compiler to use double complex variables instead of double variables.
Section 5 discusses direct application of qPATHINT to neuroscience and financial options systems. A top-level description is given of the similarities of the use of qPATHINT in these quite different systems, in the context of drawing on experiences from each system to the other, leading to new algorithms.
The Conclusion follows.
2. PHYSICAL MOTIVATIONS
2.1. SMNI
The project Statistical Mechanics of Neocortical Interactions (SMNI) has been developed in over 30+ papers since 1981, scaling aggregate synaptic interactions to describe neuronal firings, then scaling minicolumnar-macrocolumnar columns of neurons to mesocolumnar dynamics, and then scaling columns of neuronal firings to regional (sensory) macroscopic sites identified in electroencephalographic (EEG) studies [1L. Ingber, "Statistical mechanics of neocortical interactions. I. basic formulation", Physica D, vol. 5, pp. 83-107. Available from: https://www.ingber.com/ smni82_basic.pdf
[http://dx.doi.org/10.1016/0167-2789(82)90052-5] -5L. Ingber, "Statistical mechanics of neocortical interactions: Path-integral evolution of short-term memory", Physical Review E, vol. 49, no. 5, pp. 4652-4664. Available from: https://www.ingber.com/smni94_stm.pdf
[http://dx.doi.org/10.1103/PhysRevE.49.4652] [PMID: 9961760] ].
The measure of the success of SMNI has been to discover agreement/fits with experimental data from various modeled aspects of neocortical interactions, e.g., properties of short-term memory (STM) [6L. Ingber, “Columnar EEG magnetic influences on molecular development of short-term memory,” In: Short-Term Memory: New Research, G. Kalivas and S. Petralia, Eds., NY: Nova, 2012, pp. 37-72. Available from: https://www.ingber.com/smni11_stm_scales.pdf], including its capacity (auditory 7±2 and visual 4±2), duration, stability, primacy versus recency rule, as well other phenomenon, e.g., Hick’s law [7W. Hick, "On the rate of gains of information", Quarterly Journal Experimental Psychology, vol. 34, no. 4, pp. 1-33.-9A. Jensen, Individual differences in the hick paradigm.Speed of Information-Processing and Intelligence., Ablex: Norwood, NJ, pp. 101-175.], nearest-neighbor minicolumnar interactions within macrocolumns calculating rotation of images, etc [1L. Ingber, "Statistical mechanics of neocortical interactions. I. basic formulation", Physica D, vol. 5, pp. 83-107. Available from: https://www.ingber.com/ smni82_basic.pdf
[http://dx.doi.org/10.1016/0167-2789(82)90052-5] -5L. Ingber, "Statistical mechanics of neocortical interactions: Path-integral evolution of short-term memory", Physical Review E, vol. 49, no. 5, pp. 4652-4664. Available from: https://www.ingber.com/smni94_stm.pdf
[http://dx.doi.org/10.1103/PhysRevE.49.4652] [PMID: 9961760] ]. SMNI was also scaled to include mesocolumns across neocortical regions to fit EEG data [10L. Ingber, "Statistical mechanics of neocortical interactions: Applications of canonical momenta indicators to electroencephalography", Physical Review E, vol. 55, no. 4, pp. 4578-4593. Available from: https://www.ingber.com/smni97_cmi.pdf
[http://dx.doi.org/10.1103/PhysRevE.55.4578] , 6L. Ingber, “Columnar EEG magnetic influences on molecular development of short-term memory,” In: Short-Term Memory: New Research, G. Kalivas and S. Petralia, Eds., NY: Nova, 2012, pp. 37-72. Available from: https://www.ingber.com/smni11_stm_scales.pdf].
2.1.1. XSEDE EEG Project
The Extreme Science and Engineering Discovery Environment (XSEDE.org) project since February 2013, “Electroencephalographic field influence on calcium momentum waves,” fit the SMNI model to EEG data, wherein ionic Ca2+ momentum-wave effects among neuron-astrocyte-neuron tripartite synapses modified parameterization of background SMNI parameters. Direct calculations in classical and quantum physics supported the concept that the vector magnetic potential of EEG from highly synchronous firings, e.g., as measured during selective attention, might directly interact with these momentum-waves, thereby creating feedback between these ionic/quantum and macroscopic scales [6L. Ingber, “Columnar EEG magnetic influences on molecular development of short-term memory,” In: Short-Term Memory: New Research, G. Kalivas and S. Petralia, Eds., NY: Nova, 2012, pp. 37-72. Available from: https://www.ingber.com/smni11_stm_scales.pdf, 11L. Ingber, "Influence of macrocolumnar EEG on ca waves", Current Progress Journal, vol. 1, no. 1, pp. 4-8. Available from: https://www.ingber.com/smni12_vectpot.pdf
[http://dx.doi.org/10.2139/ssrn.2091676] -16P. Nunez, R. Srinivasan, and L. Ingber, Theoretical and experimental electrophysiology in human neocortex: Multiscale correlates of conscious experience.Multiscale Analysis and Nonlinear Dynamics: From genes to the brain., Wiley: New York, pp. 149-178.
[http://dx.doi.org/10.1002/9783527671632.ch06] ].
2.1.2. qPATHINT for SMNI
The present qPATHINT code can be useful to determine how the quantum regenerative process that defines Ca2+ wave-packets also may produce reasonable shocks to the waves without seriously damaging its coherence properties. A proof of principal of its use has been published [14L. Ingber, "Evolution of regenerative ca-ion wave-packet in neuronal-firing fields: Quantum path-integral with serial shocks", International Journal of Innovative Research in Information Security, vol. 4, no. 2, pp. 14-22. Available from: https://www.ingber.com/ path17_quantum_pathint_shocks.pdf].
2.2. SMFM
The project Statistical Mechanics of Financial Markets (SMFM) has been developed to model financial systems [17L. Ingber, "Statistical mechanics of nonlinear nonequilibrium financial markets", Mathematical Modelling, vol. 5, no. 6, pp. 343-361. Available from: https://www.ingber.com/markets84_statmech.pdf
[http://dx.doi.org/10.1016/0270-0255(84)90022-8] -21L. Ingber, "Automated internet trading based on optimized physics models of markets", Intelligent Internet-Based Information Processing Systems, .https://www.ingber.com/markets03_automated.pdf
[http://dx.doi.org/10.1142/9789812795342_0009] ].
2.2.1. PATHINT for Financial Options
In particular, this project has been developed to calculate financial options using PATHINT code, and a code PATHTREE [22L. Ingber, C. Chen, R.P. Mondescu, D. Muzzall, and M. Renedo, "Probability tree algorithm for general diffusion processes", Physical Review E, vol. 64, no. 5 Pt 2, p. 056702. Available from: https://www.ingber.com/path01_pathtree.pdf
[http://dx.doi.org/10.1103/PhysRevE.64.056702] [PMID: 11736136] ] based on PATHINT [23L. Ingber, "High-resolution path-integral development of financial options", Physica A, vol. 283, no. 3-4, pp. 529-558. Available from: https://www.ingber.com/markets00_highres.pdf
[http://dx.doi.org/10.1016/S0378-4371(00)00229-6] , 24L. Ingber, and J. Wilson, "Volatility of volatility of financial markets", Mathematical Computer Modelling, vol. 29, no. 5, pp. 39-57. Available from: https://www.ingber.com/markets99_vol.pdf
[http://dx.doi.org/10.1016/S0895-7177(99)00048-5] ].
2.2.2. Quantum Money
Quantum computing is here, and in the near future it will be applied to financial products, e.g., blockchains. It is not very far-fetched to assume that soon there will be financial derivatives developed on these products. Then, as is the case in classical real spaces with PATHTREE and PATHINT, qPATHTREE and qPATHINT are now poised to calculate financial derivatives in quantum complex spaces. This is beyond simply using quantum computation of financial derivatives, since the space of the dependent variables themselves may live in quantum worlds [25S. Aaronson, and P. Christiano, “Quantum money from hidden subspaces,” MIT, Cambridge, MA, Techincal Report arXiv:1203.4740 [quant-ph], 2012.
[http://dx.doi.org/10.1145/2213977.2213983] -30E. Piotrowski, M. Schroeder, and A. Zambrzycka, "Quantum extension of European option pricing based on the Ornstein-Uhlenbeck process", Physica A, vol. 368, no. 1, pp. 176-182.
[http://dx.doi.org/10.1016/j.physa.2005.12.021] ].
2.2.3. qPATHINT for Financial Options
The present qPATHINT code can be used to calculate quantum financial options. A proof of principal of its use has been published [31L. Ingber, "Options on quantum money: Quantum path-integral with serial shocks", International Journal of Innovative Research in Information Security, vol. 4, no. 2, pp. 7-13. Available from: https://www.ingber.com/path17_quantum_options_shocks.pdf].
3. PATH-INTEGRAL METHODOLOGY
3.1. Generic Applications
There are many systems that are well defined by (a) Fokker-Planck/Chapman-Kolmogorov partial-differential equations, (b) Langevin coupled stochastic-differential equations, and (c) Lagrangian or Hamiltonian path-integrals. All three such systems of equations are mathematically equivalent, when care is taken to properly take limits of discretized variables in the well-defined induced Riemannian geometry of the system due to nonlinear and time-dependent diffusions [32F. Langouche, D. Roekaerts, and E. Tirapegui, Functional Integration and Semiclassical Expansions., D. Reidel: Dordrecht, The Netherlands, .
[http://dx.doi.org/10.1007/978-94-017-1634-5] , 33L. Schulman, Techniques and Applications of Path Integration., J. Wiley and Sons: New York, .].
3.2. Path-Integral Algorithm
The path integral of a classical system of N variables indexed by i at multiple times indexed by ρ is defined in terms of its Lagrangian L:
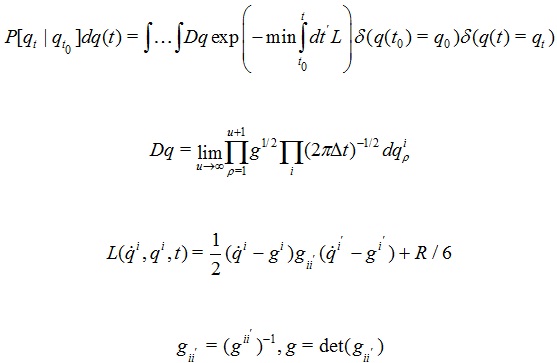 |
(1) |
Here the diagonal diffusion terms are gii and the drift terms are gi = -∂Φ/∂qi. If the diffusions terms are not constant, then there are additional terms in the drift, and in a Riemannian-curvature potential R/6 for dimension > 1 in the midpoint Stratonovich/Feynman discretization [32F. Langouche, D. Roekaerts, and E. Tirapegui, Functional Integration and Semiclassical Expansions., D. Reidel: Dordrecht, The Netherlands, .
[http://dx.doi.org/10.1007/978-94-017-1634-5] ].
The path-integral approach is particularly useful to precisely define intuitive physical variables from the Lagrangian L in terms of its underlying variables qi:
 |
(2) |
The histogram procedure recognizes that the distribution can be numerically approximated to a hight degree of accuracy by sums of rectangles of height Pi and width Δqi at points qi . For convenience just consider a one-dimensional system. In the prepoint Ito discretization, the path-integral representation can be written in terms of the kernel G, for each of its intermediate integrals, as
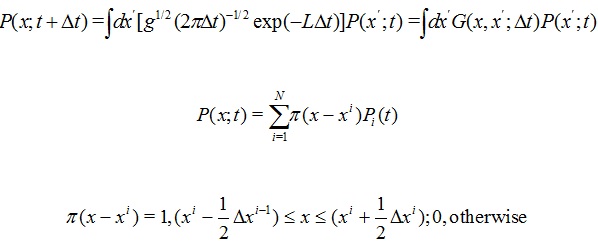 |
(3) |
This yields
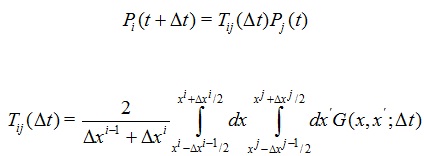 |
(4) |
Tij is a banded matrix representing the Gaussian nature of the short-time probability centered about the (possibly time-dependent) drift.
Explicit dependence of L on time t also can be included without complications. Care must be used in developing the mesh Δqi, which is strongly dependent on diagonal elements of the diffusion matrix, e.g.,
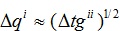 |
(5) |
This constrains the dependence of the covariance of each variable to be a (nonlinear) function of that variable to present a rectangular-ish underlying mesh. Since integration is inherently a smoothing process [34L. Ingber, "Statistical-mechanical aids to calculating term-structure models", Physical Review A, vol. 42, no. 12, pp. 7057-7064. Available from: https://www.ingber.com/markets90_interest.pdf
[http://dx.doi.org/10.1103/PhysRevA.42.7057] [PMID: 9904019] ], fitting the data with integrals over the short-time probability distribution, this permits the use of coarser meshes than the corresponding stochastic differential equation(s). For example, the coarser resolution is appropriate, typically required, for a numerical solution of the time-dependent path integral. By considering the contributions to the first and second moments, conditions on the time and variable meshes can be derived [35M. Wehner, and W. Wolfer, "Numerical evaluation of path-integral solutions to Fokker-Planck equations. I", Physical Review A, vol. 27, pp. 2663-2670.
[http://dx.doi.org/10.1103/PhysRevA.27.2663] ]. For non-zero drift, the time slice may be determined by a scan of
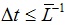 , where
, where
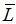 is the uniform/static Lagrangian, respecting ranges giving the most important contributions to the probability distribution P. Thus Δt can be measured by the diffusion divided by the square of the drift.
is the uniform/static Lagrangian, respecting ranges giving the most important contributions to the probability distribution P. Thus Δt can be measured by the diffusion divided by the square of the drift.
3.2.1. Direct Kernel Evaluation
Several projects have used this algorithm [36L. Ingber, and P.L. Nunez, "Statistical mechanics of neocortical interactions: High-resolution path-integral calculation of short-term memory", Physical Review E, vol. 51, no. 5, pp. 5074-5083. Available from: https://www.ingber.com/smni95_stm.pdf
[http://dx.doi.org/10.1103/PhysRevE.51.5074] [PMID: 9963220] , 37L. Ingber, R. Srinivasan, and P. Nunez, "Path-integral evolution of chaos embedded in noise: Duffing neocortical analog", Mathematical Computer Modelling, vol. 23, no. 3, pp. 43-53. Available from: https://www.ingber.com/path96_duffing.pdf
[http://dx.doi.org/10.1016/0895-7177(95)00232-4] , 24L. Ingber, and J. Wilson, "Volatility of volatility of financial markets", Mathematical Computer Modelling, vol. 29, no. 5, pp. 39-57. Available from: https://www.ingber.com/markets99_vol.pdf
[http://dx.doi.org/10.1016/S0895-7177(99)00048-5] , 35M. Wehner, and W. Wolfer, "Numerical evaluation of path-integral solutions to Fokker-Planck equations. I", Physical Review A, vol. 27, pp. 2663-2670.
[http://dx.doi.org/10.1103/PhysRevA.27.2663] , 38M. Wehner, and W. Wolfer, "Numerical evaluation of path-integral solutions to Fokker-Planck equations. II. restricted stochastic processes", Physical Review A, vol. 28, pp. 3003-3011.
[http://dx.doi.org/10.1103/PhysRevA.28.3003] , 39M.F. Wehner, and W.G. Wolfer, "Numerical evaluation of path-integral solutions to Fokker-Planck equations. III. Time and functionally dependent coefficients", Physical Review A, vol. 35, no. 4, pp. 1795-1801.
[http://dx.doi.org/10.1103/PhysRevA.35.1795] [PMID: 9898343] ]. Special 2-dimensional codes were developed for specific projects in Statistical Mechanics of Combat (SMC), SMNI and SMFM [23L. Ingber, "High-resolution path-integral development of financial options", Physica A, vol. 283, no. 3-4, pp. 529-558. Available from: https://www.ingber.com/markets00_highres.pdf
[http://dx.doi.org/10.1016/S0378-4371(00)00229-6] , 40L. Ingber, H. Fujio, and M. Wehner, "Mathematical comparison of combat computer models to exercise data", Mathematical Computer Modelling, vol. 15, no. 1, pp. 65-90. Available from: https://www.ingber.com/combat91_data.pdf
[http://dx.doi.org/10.1016/0895-7177(91)90017-2] , 36L. Ingber, and P.L. Nunez, "Statistical mechanics of neocortical interactions: High-resolution path-integral calculation of short-term memory", Physical Review E, vol. 51, no. 5, pp. 5074-5083. Available from: https://www.ingber.com/smni95_stm.pdf
[http://dx.doi.org/10.1103/PhysRevE.51.5074] [PMID: 9963220] ].
The previous 1-dimensional PATHINT code was generalized by the author to be run under N dimensions, simply using ‘make D=N‘ in the GCC Makefile. Then, a quantum generalization was made to the code, changing all variables and functions to complex variables. The generic N-dimensional code was developed for classical and quantum systems, using a small shell script called from a Makefile to set up pre-compile options [41L. Ingber, "Path-integral quantum PATHTREE and PATHINT algorithms", International Journal of Innovative Research in Information Security, vol. 3, no. 5, pp. 1-15. Available from: https://www.ingber.com/path16_quantum_path.pdf, 14L. Ingber, "Evolution of regenerative ca-ion wave-packet in neuronal-firing fields: Quantum path-integral with serial shocks", International Journal of Innovative Research in Information Security, vol. 4, no. 2, pp. 14-22. Available from: https://www.ingber.com/ path17_quantum_pathint_shocks.pdf, 31L. Ingber, "Options on quantum money: Quantum path-integral with serial shocks", International Journal of Innovative Research in Information Security, vol. 4, no. 2, pp. 7-13. Available from: https://www.ingber.com/path17_quantum_options_shocks.pdf].
3.3. Monte Carlo vs Kernels
Many path-integral numerical applications use Monte Carlo techniques [42M. O’Callaghan, and B.N. Miller, "Path integral Monte Carlo on a lattice: extended states", Physical Review E, vol. 89, no. 4, p. 042124.
[http://dx.doi.org/10.1103/PhysRevE.89.042124] [PMID: 24827210] ]. This approach includes the author’s Adaptive Simulated Annealing (ASA) code using its ASA_SAMPLE OPTIONS [43L. Ingber, “Adaptive simulated annealing (ASA),” Caltech Alumni Association, Pasadena, CA, Technical Report, Global optimization C-code, 1993. Available from: https://www.ingber.com/#ASA-CODE]. This project is concerned with serial (time-sequential) random shocks, not conveniently treated with Monte-Carlo/importance-sampling algorithms.
3.4. Scaling Issues
A “contrived” qPATHINT code was developed for quantum options, which serves to illustrate some computational scaling issues, using data and parameters from dimension 1 for all N dimensions.
The volume of the kernel required for computation is measured by [IJ]D, where D = dimension, I is the number of elements in the diagonal (or the drift-shifted diagonal in some cases), J is the width of the off-diagonal. Many loops in the code also have D-dependent inner loops. J has been as high as 13, requiring a span of 13+13+1 = 27 elements, needed for some oscillatory systems in previous studies [14L. Ingber, "Evolution of regenerative ca-ion wave-packet in neuronal-firing fields: Quantum path-integral with serial shocks", International Journal of Innovative Research in Information Security, vol. 4, no. 2, pp. 14-22. Available from: https://www.ingber.com/ path17_quantum_pathint_shocks.pdf]; in contrast, currently [q]PATHTREE is only a binary tree with J. Note that scales as sqrt(E), where E = number epochs in [t0 , T] (the diffusion is proportional to dt1/2). I is determined in each dimension, by dqi that must span [qmin, qmax], where dqi = (dtgii)1/2,dt = (T -t0 )/E.
Examples for this paper were done with with J = 3, T = 1.5, t0 = 0, qmin = 1, qmax = 12, I = imxall J = jmxall Prob_Mesh_Size=ijkcnt=number-nonzero-elements. For larger J and/or larger E, it is possible to decrease E and T, such that fewer meshes can be developed, and qPATHINT would propagate from t0 to T_1, from T_1 to T_2, ..., from T_s-1 to T_s=T, with write/read of probabilities/wave-functions developed at each intermediate T_[].
Runs were done for 16 Strikes for an American option [44J. Hull, Options, Futures, and Other Derivatives., 4th edPrentice Hall: Upper Saddle River, NJ, .] (each Strike require independent propagation of the distribution), requiring a total of 1364 foldings.
To appreciate requirements of kernel memory as a function of dimension, for the mesh considered in this pilot study,
D=1:imxall: 27, jmxall: 7, ijkcnt: 189
D=2:imxall: 729, jmxall: 49, ijkcnt: 35721
D=3:imxall: 19683, jmxall: 343, ijkcnt: 6751269
D=4:imxall: 531441, jmxall: 2401, ijkcnt: 1275989841
D=5:imxall: 14348907, jmxall: 16807, ijkcnt: 241162079949
D=6:imxall: 387420489, jmxall: 117649, ijkcnt: 45579633110361
D=7:imxall: 10460353203, jmxall: 823543, ijkcnt: 8614550657858229
where =imxall, =jmxall, and kernel size = ijkcnt.
The results to date show that D=3 is reasonable with current systems constraints. D=4 is only possible with very long run times exceeding 47 CPU hours on XSEDE San Diego Supercomputer (SDSC.edu) Comet. D=5,6 are possible, but not one epoch evolution completed within 47 CPU hours on Comet. Comet is a 2.0 Petaflop (PF) Dell integrated compute cluster, with next-generation Intel Haswell processors (with AVX2), interconnected with Mellanox FDR InfiniBand in a hybrid fat-tree topology. Full bisection bandwidth is available at rack level (72 nodes) and there is a 4:1 oversubscription cross-rack. Compute nodes feature 320 GB of SSD storage and 128GB of DRAM per node.
Attempting D=7 leads directly to ’*** laginit = 9 ***’, where the code crashes with too large ’(long int) imxall’:
if ((pnew = (double complex *) calloc (imxall, sizeof (double complex))) == NULL) return (9);
The same results are obtained with ’(long long int) imxall’, which reverts to ’(long int) imxall’ on most platforms.
It is possible to run the code saving all elements of the kernel is a large matrix, instead of calculating the Lagrangian and its kernel each evolution. However, this is not useful for time-dependent problems as considered here, and the ijkcnt-size of memory required prevents any runs with dimension > 3.
4. QUANTUM PATH INTEGRAL ALGORITHMS
4.1. Imaginary Time
Imaginary-time Wick rotations transform imaginary time (the primary source of imaginary dependencies) into a real-variable time. However, when used with numerical calculations, after multiple foldings of the path integral, usually there is no audit trail back to imaginary time to extract phase information (private communication with several authors of path-integral papers, including Larry Schulman on 18 Nov 2015) [33L. Schulman, Techniques and Applications of Path Integration., J. Wiley and Sons: New York, .].
4.2. SMNI
Previous papers have modeled minicolumns as wires which support neuronal firings, mainly from large neocortical excitatory pyramidal cells in layer V (of I-VI), giving rise to currents which in turn gives rise to electric potentials measured as scalp EEG [45L. Ingber, “Computational algorithms derived from multiple scales of neocortical processing,” In: Pointing at Boundaries: Integrating Computation and Cognition on Biological Grounds, A. Pereira, E. Massad, and N. Bobbitt, Eds., Springer: New York, 2011, pp. 1-13. Invited Paper. Available from: https://www.ingber.com/smni11_cog_comp.pdf, 6L. Ingber, “Columnar EEG magnetic influences on molecular development of short-term memory,” In: Short-Term Memory: New Research, G. Kalivas and S. Petralia, Eds., NY: Nova, 2012, pp. 37-72. Available from: https://www.ingber.com/smni11_stm_scales.pdf, 16P. Nunez, R. Srinivasan, and L. Ingber, Theoretical and experimental electrophysiology in human neocortex: Multiscale correlates of conscious experience.Multiscale Analysis and Nonlinear Dynamics: From genes to the brain., Wiley: New York, pp. 149-178.
[http://dx.doi.org/10.1002/9783527671632.ch06] ]. This gives rise to a magnetic vector potential
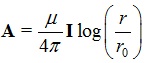 |
(6) |
which has a log-insensitive dependence on distance. In the brain, µ ≈ µ0 , where is the magnetic permeability in vacuum = 4π10-7 H/m (Henry/meter), where Henry has units of kg-m-C-2, the conversion factor from electrical to mechanical variables. For oscillatory waves, the magnetic field B =
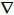 × A; and the electric field
× A; and the electric field
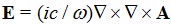 do not have this log dependence on distance. Thus, A fields can contribute collectively over large regions of neocortex [6L. Ingber, “Columnar EEG magnetic influences on molecular development of short-term memory,” In: Short-Term Memory: New Research, G. Kalivas and S. Petralia, Eds., NY: Nova, 2012, pp. 37-72. Available from: https://www.ingber.com/smni11_stm_scales.pdf, 11L. Ingber, "Influence of macrocolumnar EEG on ca waves", Current Progress Journal, vol. 1, no. 1, pp. 4-8. Available from: https://www.ingber.com/smni12_vectpot.pdf
do not have this log dependence on distance. Thus, A fields can contribute collectively over large regions of neocortex [6L. Ingber, “Columnar EEG magnetic influences on molecular development of short-term memory,” In: Short-Term Memory: New Research, G. Kalivas and S. Petralia, Eds., NY: Nova, 2012, pp. 37-72. Available from: https://www.ingber.com/smni11_stm_scales.pdf, 11L. Ingber, "Influence of macrocolumnar EEG on ca waves", Current Progress Journal, vol. 1, no. 1, pp. 4-8. Available from: https://www.ingber.com/smni12_vectpot.pdf
[http://dx.doi.org/10.2139/ssrn.2091676] -16P. Nunez, R. Srinivasan, and L. Ingber, Theoretical and experimental electrophysiology in human neocortex: Multiscale correlates of conscious experience.Multiscale Analysis and Nonlinear Dynamics: From genes to the brain., Wiley: New York, pp. 149-178.
[http://dx.doi.org/10.1002/9783527671632.ch06] ]. The magnitude of the current is taken from experimental data on dipole moments Q =| I | where
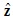 is the direction of the current I with the dipole spread over z. Q ranges from 1 pA-m = 10-12 A-m for a pyramidal neuron [46S. Murakami, and Y. Okada, "Contributions of principal neocortical neurons to magnetoencephalography and electroencephalography signals", Journal of Physiology, vol. 575, no. Pt 3, pp. 925-936.
is the direction of the current I with the dipole spread over z. Q ranges from 1 pA-m = 10-12 A-m for a pyramidal neuron [46S. Murakami, and Y. Okada, "Contributions of principal neocortical neurons to magnetoencephalography and electroencephalography signals", Journal of Physiology, vol. 575, no. Pt 3, pp. 925-936.
[http://dx.doi.org/10.1113/jphysiol.2006.105379] [PMID: 16613883] ], to 10-9 A-m for larger neocortical mass [47P. Nunez, and R. Srinivasan, Electric Fields of the Brain: The Neurophysics of EEG., 2nd edOxford University Press: London, .
[http://dx.doi.org/10.1093/acprof:oso/9780195050387.001.0001] ]. These currents give rise to qA≈10-28 kg-m/s. The velocity of a Ca2+ wave can be ≈20-50 µm/s. In neocortex, a typical Ca+2 wave of 1000 ions, with total mass m=6.655×10-23 kg times a speed of ≈20-50 µm/s, gives p≈10-27 kg-m/s.
Without random shocks, the wave function ψe representing the interaction of the EEG magnetic vector potential A with the momenta p of Ca2+ wave packets was derived to be [14L. Ingber, "Evolution of regenerative ca-ion wave-packet in neuronal-firing fields: Quantum path-integral with serial shocks", International Journal of Innovative Research in Information Security, vol. 4, no. 2, pp. 14-22. Available from: https://www.ingber.com/ path17_quantum_pathint_shocks.pdf]
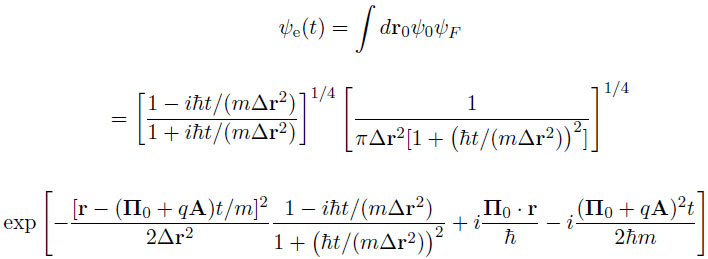 |
(7) |
where ψ0 is the initial Gaussian packet, ψF is the free-wave evolution operator,
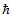 is the Planck constant, q is the electronic charge of Ca2+ ions, m is the mass of a wave-packet of 1000 Ca2+ ions, Δr2 is the spatial variance of the wave-packet, the initial canonical momentum is II0 = p0 + qA0 , and the evolving canonical momentum is II = P+qA. Detailed classical and quantum calculations have shown that P of the Ca2+ wave packet and qA of the large-scale EEG field make about equal contributions to II.
is the Planck constant, q is the electronic charge of Ca2+ ions, m is the mass of a wave-packet of 1000 Ca2+ ions, Δr2 is the spatial variance of the wave-packet, the initial canonical momentum is II0 = p0 + qA0 , and the evolving canonical momentum is II = P+qA. Detailed classical and quantum calculations have shown that P of the Ca2+ wave packet and qA of the large-scale EEG field make about equal contributions to II.
This calculation is for any time t, so the path integral was folded over many times numerically to give agreement with this results for long times [14L. Ingber, "Evolution of regenerative ca-ion wave-packet in neuronal-firing fields: Quantum path-integral with serial shocks", International Journal of Innovative Research in Information Security, vol. 4, no. 2, pp. 14-22. Available from: https://www.ingber.com/ path17_quantum_pathint_shocks.pdf]. Then, the path integral was calculated with random shocks to find a reasonable threshold that still possessed the character of the original wave function.
All this was done for a one-dimensional system. EEG is produced primarily by highly synchronous firings of pyramidal neurons, also the source of A fields, relatively orthogonal to the 6 layers of neocortex. A realistic calculation would require a 3-dimensional calculation over sets of input parameters. After this, contact with real EEG must be made to see if better fits are obtained including this more realistic modeling of Ca2+ -wave interaction with EEG than in previous XSEDE studies [13L. Ingber, "Statistical mechanics of neocortical interactions: Large-scale EEG influences on molecular processes", Journal of Theoretical Biology, vol. 395, pp. 144-152. Available from: https://www.ingber.com/smni16_large-scale_molecular.pdf
[http://dx.doi.org/10.1016/j.jtbi.2016.02.003] [PMID: 26874226] -15L. Ingber, M. Pappalepore, and R.R. Stesiak, "Electroencephalographic field influence on calcium momentum waves", Journal of Theoretical Biology, vol. 343, pp. 138-153. Available from: https://www.ingber.com/smni14_EEG_ca.pdf
[http://dx.doi.org/10.1016/j.jtbi.2013.11.002] [PMID: 24239957] ]. This will require coupling models of ψ with the current SMNI model as discussed in the next section.
4.2.1. Assumptions for Quantum SMNI
There are assumptions made for this quantum enhancement of SMNI that can only be determined by future experiments.
In the context of quantum mechanics, the wave function of the Ca2+ wave packet was calculated, and it was demonstrated that overlap with multiple collisions, due to their regenerative processes, during the observed long durations of hundreds of ms of typical Ca2+ waves [12L. Ingber, Calculating consciousness correlates at multiple scales of neocortical interactions,” in Horizons in Neuroscience Research, A. Costa and E. Villalba, Eds., NY: Nova, 2015, pp. 153-186, ISBN: 978-1-63482-632-7 Available from: https://www.ingber.com/ smni15_calc_conscious.pdf-15L. Ingber, M. Pappalepore, and R.R. Stesiak, "Electroencephalographic field influence on calcium momentum waves", Journal of Theoretical Biology, vol. 343, pp. 138-153. Available from: https://www.ingber.com/smni14_EEG_ca.pdf
[http://dx.doi.org/10.1016/j.jtbi.2013.11.002] [PMID: 24239957] ] support a Zeno or “bang-bang” effect [48P. Facchi, D. Lidar, and S. Pascazio, "Unification of dynamical decoupling and the quantum Zeno effect", Physical Review A, vol. 69, no. 032314, pp. 1-6.-55P. Zhang, Q. Ai, Y. Li, D. Xu, and C. Sun, "Dynamics of quantum Zeno and anti-Zeno effects in an open system", Science China Physics, Mechanics and Astronomy, vol. 57, no. 2, pp. 194-207.
[http://dx.doi.org/10.1007/s11433-013-5377-x] ] which may promote long coherence times.
Of course, the Zeno/“bang-bang” effect may exist only in special contexts, since decoherence among particles is known to be very fast, e.g., faster than phase-damping of macroscopic classical particles colliding with quantum particles [56J. Preskill, "Quantum mechanics,” Caltech, Pasadena, CA, Technical Report, Lecture Notes, 2015", Available from: http://www.theory.caltech.edu/people/preskill/ph219/]. Here, the constant collisions of Ca2+ ions as they enter and leave the Ca2+ wave packet due to the regenerative process that maintains the wave, may perpetuate at least part of the wave, permitting the Zeno/“bang-bang” effect. In any case, qPATHINT as used here provides an opportunity to explore the coherence stability of the wave due to serial shocks of this process.
4.2.2. Free Will
In addition to the intrinsic interest of researching STM and multiple scales of neocortical interactions via EEG data, there is interest in researching possible quantum influences on highly synchronous neuronal firings relevant to STM to understand possible connections to consciousness and “Free Will” (FW).
As pointed out in some recent papers [13L. Ingber, "Statistical mechanics of neocortical interactions: Large-scale EEG influences on molecular processes", Journal of Theoretical Biology, vol. 395, pp. 144-152. Available from: https://www.ingber.com/smni16_large-scale_molecular.pdf
[http://dx.doi.org/10.1016/j.jtbi.2016.02.003] [PMID: 26874226] , 41L. Ingber, "Path-integral quantum PATHTREE and PATHINT algorithms", International Journal of Innovative Research in Information Security, vol. 3, no. 5, pp. 1-15. Available from: https://www.ingber.com/path16_quantum_path.pdf], if neuroscience ever establishes experimental feedback from quantum-level processes of tripartite synaptic interactions with large-scale synchronous neuronal firings, that are now recognized as being highly correlated with STM and states of attention, then FW may yet be established using the quantum no-clone “Free Will Theorem” (FWT) [57J. Conway, and S. Kochen, “The free will theorem,” Princeton U, Princeton, NJ, Technical Report, arXiv:quant-ph/0604079 [quant-ph], 2006.
[http://dx.doi.org/10.1007/s10701-006-9068-6] , 58J. Conway, and S. Kochen, "The strong free will theorem", Notices of the American Mathematical Society, vol. 56, no. 2, pp. 226-232.]. Attentional processes are considered to be an integral part of consciousness [59S. Dehaene, H. Lau, and S. Kouider, "What is consciousness, and could machines have it?", Science, vol. 358, no. 6362, pp. 486-492.
[http://dx.doi.org/10.1126/science.aan8871] [PMID: 29074769] ].
Basically, this means that a Ca2+quantum wave-packet may generate a state proven to have not previously existed; quantum states cannot be cloned. In the context of the basic premise of this paper, this state may be influential in a large-scale pattern of synchronous neuronal firings, thereby rendering this pattern as a truly new pattern not having previously existed. The FWT shows that this pattern, considered as a measurement of the Ca2+ quantum wave-packet, is correctly identified as itself being a new decision not solely based on previous decisions, even under reasonably stochastic experimental and real-life conditions.
Only recently has the core SMNI hypothesis since circa 1980 [60L. Ingber, "Towards a unified brain theory", Journal Social Biological Structures, vol. 4, pp. 211-224. Available from: https://www.ingber.com/smni81_unified.pdf
[http://dx.doi.org/10.1016/S0140-1750(81)80037-1] , 1L. Ingber, "Statistical mechanics of neocortical interactions. I. basic formulation", Physica D, vol. 5, pp. 83-107. Available from: https://www.ingber.com/ smni82_basic.pdf
[http://dx.doi.org/10.1016/0167-2789(82)90052-5] , 2L. Ingber, "Statistical mechanics of neocortical interactions. dynamics of synaptic modification", Physical Review A, vol. 28, pp. 395-416. Available from: https://www.ingber.com/smni83_dynamics.pdf
[http://dx.doi.org/10.1103/PhysRevA.28.395] ], that highly synchronous patterns of neuronal firings in fact process high-level information, been verified experimentally [61J. Asher, "Brain’s code for visual working memory deciphered in monkeys NIH-funded study,” NIH, Bethesda, MD, Technical Report, NIH Press Release, 2012", Available from: http://www.nimh.nih.gov/news/ science-news/2012/in-sync-brain-waves-hold-memory-of-objects-just-seen.shtml, 62R.F. Salazar, N.M. Dotson, S.L. Bressler, and C.M. Gray, "Content-specific fronto-parietal synchronization during visual working memory", Science, vol. 338, no. 6110, pp. 1097-1100.
[http://dx.doi.org/10.1126/science.1224000] [PMID: 23118014] ].
Clearly, even in the above context, for most people most of the time, internal and external events affecting neural probabilistic patterns of attention [63A. Pouget, J.M. Beck, W.J. Ma, and P.E. Latham, "Probabilistic brains: knowns and unknowns", Nature Neuroscience, vol. 16, no. 9, pp. 1170-1178.
[http://dx.doi.org/10.1038/nn.3495] [PMID: 23955561] ] give rise to quite practical reasonable FW. However, there also may be some Science that establishes a truly precise FW.
4.2.3. SMNI Context
A short description of the SMNI structure is required to understand how the qPATHINT development is used in this multiple-scale model [13L. Ingber, "Statistical mechanics of neocortical interactions: Large-scale EEG influences on molecular processes", Journal of Theoretical Biology, vol. 395, pp. 144-152. Available from: https://www.ingber.com/smni16_large-scale_molecular.pdf
[http://dx.doi.org/10.1016/j.jtbi.2016.02.003] [PMID: 26874226] ].
After a statistical-mechanical aggregation of synaptic, neuronal and columnar scales [1L. Ingber, "Statistical mechanics of neocortical interactions. I. basic formulation", Physica D, vol. 5, pp. 83-107. Available from: https://www.ingber.com/ smni82_basic.pdf
[http://dx.doi.org/10.1016/0167-2789(82)90052-5] , 2L. Ingber, "Statistical mechanics of neocortical interactions. dynamics of synaptic modification", Physical Review A, vol. 28, pp. 395-416. Available from: https://www.ingber.com/smni83_dynamics.pdf
[http://dx.doi.org/10.1103/PhysRevA.28.395] ], the SMNI Lagrangian L in the prepoint (Ito) representation is
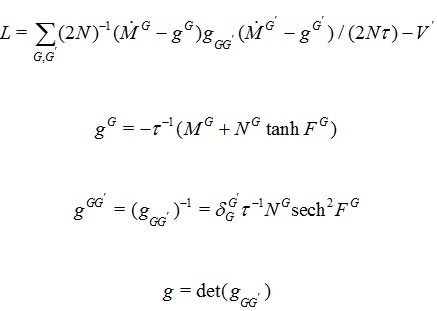 |
(8) |
where G = {E,I} for chemically independent excitatory and inhibitory synaptic interactions. All values of parameters were taken within ranges of experimental data: NG = {NE =160, NI =60} was chosen for visual neocortex, {NE =80, NI =30} was chosen for all other neocortical regions, MG' and NG' in FG are afferent macrocolumnar firings scaled to efferent minicolumnar firings by N/N* ≈ 10-3 , and N* is the number of neurons in a macrocolumn, about 105.V' includes nearest-neighbor mesocolumnar interactions [1L. Ingber, "Statistical mechanics of neocortical interactions. I. basic formulation", Physica D, vol. 5, pp. 83-107. Available from: https://www.ingber.com/ smni82_basic.pdf
[http://dx.doi.org/10.1016/0167-2789(82)90052-5] , 2L. Ingber, "Statistical mechanics of neocortical interactions. dynamics of synaptic modification", Physical Review A, vol. 28, pp. 395-416. Available from: https://www.ingber.com/smni83_dynamics.pdf
[http://dx.doi.org/10.1103/PhysRevA.28.395] ]. τ is usually considered to be on the order of 5-10 ms. The threshold factor FG is derived as
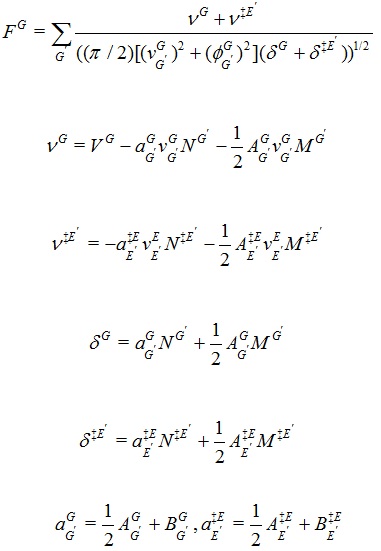 |
(9) |
where AGG' is the columnar-averaged direct synaptic efficacy, BGG' is the columnar-averaged background-noise contribution to synaptic efficacy. AGG' and BGG' have been scaled by N* / N ≈ 10-3 keeping FG invariant. Other values are consistent with experimental data, e.g., VG=10 mV, vGG' =0.1 mV,ϕGG' =0.031/2 mV. The
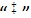 parameters arise from regional interactions across many macrocolumns.
parameters arise from regional interactions across many macrocolumns.
Three basic models were developed with slight adjustments of the parameters [3L. Ingber, "Statistical mechanics of neocortical interactions. derivation of short-term-memory capacity", Physical Review A, vol. 29, pp. 3346-3358. Available from: https://www.ingber.com/smni84_stm.pdf
[http://dx.doi.org/10.1103/PhysRevA.29.3346] ], changing the firing component of the columnar-averaged efficacies
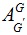 within experimental ranges, which modify FG threshold factors to yield (a) case EC, dominant excitation subsequent firings in the conditional probability, or (b) case IC, inhibitory subsequent firings, or (c) case BC, balanced between EC and IC. A Centering Mechanism (CM) on case BC yields case wherein the numerator of FG only has terms proportional to ME', MI' and
within experimental ranges, which modify FG threshold factors to yield (a) case EC, dominant excitation subsequent firings in the conditional probability, or (b) case IC, inhibitory subsequent firings, or (c) case BC, balanced between EC and IC. A Centering Mechanism (CM) on case BC yields case wherein the numerator of FG only has terms proportional to ME', MI' and
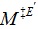 , i.e., zeroing other constant terms by resetting the background parameters
, i.e., zeroing other constant terms by resetting the background parameters
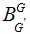 , still within experimental ranges. This has the net effect of bringing in a maximum number of minima into the physical firing MG -space. The minima of the numerator then defines a major parabolic trough,
, still within experimental ranges. This has the net effect of bringing in a maximum number of minima into the physical firing MG -space. The minima of the numerator then defines a major parabolic trough,
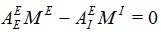 |
(10) |
about which other SMNI nonlinearities bring in multiple minima calculated to be consistent with STM phenomena. Here, A dynamic CM (DCM) model is used [13L. Ingber, "Statistical mechanics of neocortical interactions: Large-scale EEG influences on molecular processes", Journal of Theoretical Biology, vol. 395, pp. 144-152. Available from: https://www.ingber.com/smni16_large-scale_molecular.pdf
[http://dx.doi.org/10.1016/j.jtbi.2016.02.003] [PMID: 26874226] ], wherein
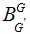 the are reset every few epochs of τ, parameterized to include contributions from tripartite neuron-astrocyte-neuron contributions. PATHINT also has been successfully used with the SMNI Lagrangian L to calculate properties of STM for both auditory and visual memory [64K.A. Ericsson, and W.G. Chase, "Exceptional memory", American Scientist, vol. 70, no. 6, pp. 607-615.
the are reset every few epochs of τ, parameterized to include contributions from tripartite neuron-astrocyte-neuron contributions. PATHINT also has been successfully used with the SMNI Lagrangian L to calculate properties of STM for both auditory and visual memory [64K.A. Ericsson, and W.G. Chase, "Exceptional memory", American Scientist, vol. 70, no. 6, pp. 607-615.
[PMID: 7181217] , 65G.J. Zhang, and H.A. Simon, "STM capacity for Chinese words and idioms: chunking and acoustical loop hypotheses", Memory and Cognition, vol. 13, no. 3, pp. 193-201.
[http://dx.doi.org/10.3758/BF03197681] [PMID: 4046819] ] calculating the stability and duration of STM, the observed 7 ± 2; capacity rule of auditory memory and the observed 4 ± 2 capacity rule of visual memory [23L. Ingber, "High-resolution path-integral development of financial options", Physica A, vol. 283, no. 3-4, pp. 529-558. Available from: https://www.ingber.com/markets00_highres.pdf
[http://dx.doi.org/10.1016/S0378-4371(00)00229-6] , 36L. Ingber, and P.L. Nunez, "Statistical mechanics of neocortical interactions: High-resolution path-integral calculation of short-term memory", Physical Review E, vol. 51, no. 5, pp. 5074-5083. Available from: https://www.ingber.com/smni95_stm.pdf
[http://dx.doi.org/10.1103/PhysRevE.51.5074] [PMID: 9963220] ].
4.3. SMFM
Options models describe the market value of an option, V as
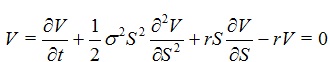 |
(11) |
where S is the asset price, and σ is the standard deviation, or volatility of S, and r is the short-term interest rate.
The basic Black-Scholes (BS) options model [66F. Black, and M. Scholes, "The pricing of options and corporate liabilities", The Journal of Political Economy, vol. 81, pp. 637-659.
[http://dx.doi.org/10.1086/260062] ] considers a portfolio Π in terms of Δ,
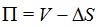 |
(12) |
in a market with Gaussian-Markovian (“white”) noise X and drift µ ,
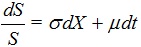 |
(13) |
where V(S,t) inherits a random process from S,
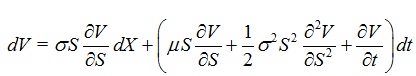 |
(14) |
This yields
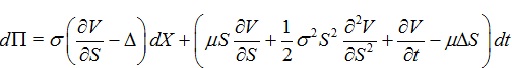 |
(15) |
Financial options are generally described and traded using “Greeks”:
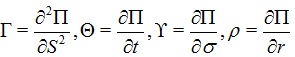 |
(16) |
The portfolio to be hedged is often considered to be “risk-neutral,” if Δ is chosen such that
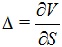 |
(17) |
The expected risk-neutral return of Π is
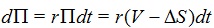 |
(18) |
where S is the asset price σ, and is the standard deviation, or volatility of S, and r is the short-term interest rate. For example, the basic equation can apply to many models of interpretations of prices given to V, e.g., puts or calls, and to S, e.g., stocks or futures, dividends, etc.
Path-integral algorithms are very useful for the calculation of the evolving probability distribution defined by this stochastic system, especially for realistic non-Black-Scholes financial options requiring time-dependent nonlinear drifts and diffusions, e.g., as developed by the author [23L. Ingber, "High-resolution path-integral development of financial options", Physica A, vol. 283, no. 3-4, pp. 529-558. Available from: https://www.ingber.com/markets00_highres.pdf
[http://dx.doi.org/10.1016/S0378-4371(00)00229-6] , 24L. Ingber, and J. Wilson, "Volatility of volatility of financial markets", Mathematical Computer Modelling, vol. 29, no. 5, pp. 39-57. Available from: https://www.ingber.com/markets99_vol.pdf
[http://dx.doi.org/10.1016/S0895-7177(99)00048-5] ]. In particular, American options (with possible early exercise), the most popular options and calculated here, have no closed solutions and must be done numerically. Other authors also have applied classical path-integral techniques to options [67B. Balaji, "Option pricing formulas and nonlinear filtering: a Feynman path integral perspective", Signal Processing, Sensor Fusion, and Target Recognition XXII, vol. 8745, pp. 1-10.
[http://dx.doi.org/10.1117/12.2017901] ].
Dividends and stress-testing for possible future events require including “shocks” to the system. A 1-dimensional calculation of quantum options using qPATHINT with shocks was published [31L. Ingber, "Options on quantum money: Quantum path-integral with serial shocks", International Journal of Innovative Research in Information Security, vol. 4, no. 2, pp. 7-13. Available from: https://www.ingber.com/path17_quantum_options_shocks.pdf]. Future studies including volatility of volatility [23L. Ingber, "High-resolution path-integral development of financial options", Physica A, vol. 283, no. 3-4, pp. 529-558. Available from: https://www.ingber.com/markets00_highres.pdf
[http://dx.doi.org/10.1016/S0378-4371(00)00229-6] ] are required to better understand quantum financial options.
4.3.1. Blockchains
As in SMNI, here too the core of the quantum no-clone “Free Will Theorem” (FWT) theorem can have important applications. Quantum currency cannot be cloned. Such currencies are exceptional candidates for very efficient blockchains, e.g., since each “coin” has a unique identity [25S. Aaronson, and P. Christiano, “Quantum money from hidden subspaces,” MIT, Cambridge, MA, Techincal Report arXiv:1203.4740 [quant-ph], 2012.
[http://dx.doi.org/10.1145/2213977.2213983] , 28J. Jogenfors, “Quantum bitcoin: An anonymous and distributed currency secured by the no-cloning theorem of quantum mechanics,” Linkoping U, Linkoping, Sweden, Techincal Report arXiv:1604.01383 [quant-ph], 2016., 29K. Meyer, “Extending and simulating the quantum binomial options pricing model,” U Manitoba, Winnipeg, Canada, Techincal Report Thesis, 2009. Available from: http://hdl.handle.net/1993/3154].
As in SMNI, here too there are issues about the decoherence time of such “coins”.
5. APPLICATIONS OF qPATHINT FOR SMNI AND SMFM
While these two systems, SMNI and SMFM, are quite different, the use of qPATHINT is envisioned to be quite similar.
5.1. SMFM
For SMFM, the use of qPATHINT for quantum options is similar to the use of PATHINT for classical options. For PATHINT, the probability distribution of the underlying (e.g., “price”) is propagated from its initial state, numerically growing into a tree of probability nodes. Then, starting backward from the final time at the maturity date of the option, at each node a calculation is performed, e.g., for American options comparing the strike price to the price at that node, and a decision is made, e.g., whether to exercise the option at that node, etc. Other calculations also can be made at each node or time slices of nodes, e.g., of Greeks that might enter decisions that can be applied to classical events, inclusion of dividends, changes of interest rates, etc.
For qPATHINT, the evolving distribution might itself represent monetary value, a link in a quantum blockchain, a “wave-function” itself whose associated probability (complex square) is the entity being traded, etc. For quantum options, the nature of the evolving distribution likely would be determined by the market. Experience with the pilot SMNI test demonstrates the need for wide kernel bands for oscillatory systems.
For classical PATHINT, previous publications have shown how real-life strike data is successfully fit/predicted for use in trading financial options [23L. Ingber, "High-resolution path-integral development of financial options", Physica A, vol. 283, no. 3-4, pp. 529-558. Available from: https://www.ingber.com/markets00_highres.pdf
[http://dx.doi.org/10.1016/S0378-4371(00)00229-6] , 22L. Ingber, C. Chen, R.P. Mondescu, D. Muzzall, and M. Renedo, "Probability tree algorithm for general diffusion processes", Physical Review E, vol. 64, no. 5 Pt 2, p. 056702. Available from: https://www.ingber.com/path01_pathtree.pdf
[http://dx.doi.org/10.1103/PhysRevE.64.056702] [PMID: 11736136] , 24L. Ingber, and J. Wilson, "Volatility of volatility of financial markets", Mathematical Computer Modelling, vol. 29, no. 5, pp. 39-57. Available from: https://www.ingber.com/markets99_vol.pdf
[http://dx.doi.org/10.1016/S0895-7177(99)00048-5] ]. Similarly, qPATHINT can be tested when quantum strikes or other traded entities become available.
5.2. SMNI
For SMNI, the use of qPATHINT is envisioned to be similar to its use for SMFM. The wave function ψ is propagated for its initial state, numerically growing into a tree of wave-function nodes. At each node, going forward instead of back in time as for SMFM, interaction of the Ca2+ of wave-packet, via its momentum P, with highly synchronous EEG, via its collective magnetic vector potential A, is calculated to determine changes due to time-dependent phenomena. Such changes occur at microscopic scales, e.g., due to modifications of the regenerative wave-packet as ions leave and contribute to the wave packet, thereby determining the effect on tripartite contributions to neuron-astrocyte-neuron synaptic activity, affecting both P and A. Such changes also may occur at macroscopic scales, e.g., changes due to external and internal stimuli affecting synchronous firings and thereby A . At every time slice, quantum effects on synaptic interactions are determined by expected values of the interactions over probabilities(ψ*ψ) determined by the wave-functions at their nodes.
Previous publications have shown how real-life EEG data, under experimental paradigms measuring attentional states with varying conditions ranging from studies of alcoholism to different stimuli presented to subjects, can be used to fit the SMNI description of multiple scales of neocortical activity, e.g., including synaptic variables and parameters, collective columnar firings within large regions of neocortex, etc. Recent papers have included models of Ca2+ -waves modifying parameterization of background SMNI synaptic parameters. Data was fit to this model using the author’s Adaptive Simulated Annealing code [43L. Ingber, “Adaptive simulated annealing (ASA),” Caltech Alumni Association, Pasadena, CA, Technical Report, Global optimization C-code, 1993. Available from: https://www.ingber.com/#ASA-CODE, 68L. Ingber, Adaptive simulated annealing.Stochastic global optimization and its applications with fuzzy adaptive simulated annealing., Springer: New York, pp. 33-61. Available from: https://www.ingber.com/asa11_options.pdf.. ]. These projects demonstrated that fits with this inclusion were better than fits without.
Using qPATHINT, quantum scales of interaction can now be included. Again, a reasonable measure of the influence of these scales will be to fit real EEG data under other published experimental paradigms. This will be accomplished using the above calculation of ψ(t) with realistic serial shocks, calculating updates to P(t) and A(t) at each time slice corresponding to the EEG data for both training and testing sets of data. While PATHINT could synchronously also be evolved using the SMNI Lagrangian, i.e., considering a joint quantum-classical probability distribution, it likely is convenient and accurate to use the short-term SMNI Lagrangian as in previous studies to fit EEG and at each epoch; note that the columnar neocortical system propagates slower than the faster Ca2+ wave-packet system. This permits a robust inclusion of quantum-scale interactions into the SMNI multiple-scale framework.
An additional burden of reality is of course placed on the specific (P+qA) interaction developed since 2012, between P of Ca2+ wave packets and qA from EEG fields. However, the methodology developed here still will be useful for other interactions that might be relevant to include these expanded multiple scales of neocortical interactions.
CONCLUSION
A summary of a kernel numerical path-integral methodology is presented, with emphasis on two different systems, in neuroscience and financial markets. Both SMNI and SMFM are generalized by including quantum variables using qPATHINT. The SMFM method of calculation of financial options used at each time slice is now adopted for SMNI. SMFM will require similar large kernel bands for oscillatory states.
In financial markets, the SMFM model has demonstrated it is faithful to experimental data, e.g., financial options traded in real financial markets, using the classical PATHINT algorithm. qPATHINT now permits calculation of quantum options with serial shocks on quantum money, by evolving the quantum distribution of a quantum price variable, and calculating early exercise by calculating comparisons or price with strikes at each node at each time slice, marching back in time from the option maturity date.
In neuroscience, the SMNI model has demonstrated it is faithful to experimental data, e.g., STM and EEG recordings under STM experimental paradigms. qPATHINT now permits a new inclusion of quantum scales in the multiple-scale SMNI model, by evolving Ca2+ wave-packets with momentum P, with serial shocks, interacting with the magnetic vector potential A derived from EEG data, via a (P+qA) interaction, calculated at each node at each time slice, marching forward in time lock-step with experimental EEG data. This presents a time-dependent propagation of interacting quantum and classical scales.
Published pilot studies give a rationale for further developing this particular quantum path-integral algorithm based on folding kernels, as this can be used to study serial random shocks that occur in many real systems. Furthermore, this quantum version can be used for many quantum systems, which are becoming increasingly important as experimental data is increasing at a rapid pace for many quantum systems.
The SMNI neuroscience project will be enhanced using a new algorithm, offering more realistic studies of potential quantum interactions calculated in 3 dimensions.
The SMFM financial options project will be enhanced by more realistic studies of quantum money and quantum options that include volatility of volatility, requiring at least 2 dimensions.
CONSENT FOR PUBLICATION
Not applicable
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The author thanks the Extreme Science and Engineering Discovery Environment (XSEDE.org), for three supercomputer grants since February 2013, “Electroencephalographic field influence on calcium momentum waves”, one under PHY130022 and two under TG-MCB140110. The current grant also under TG-MCB140110, “Quantum path-integral qPATHTREE and qPATHINT algorithms”, runs through December 2017.
This paper was the core of a successful Extreme Science and Engineering Discovery Environment (https://www.xsede.org) renewal grant for Jan-Dec 2018. XSEDE grants since Feb 2013 have spanned several projects described in https://www.ingber.com/lir_computational_physics_group.html.
REFERENCES
| [1] | L. Ingber, "Statistical mechanics of neocortical interactions. I. basic formulation", Physica D, vol. 5, pp. 83-107. Available from: https://www.ingber.com/ smni82_basic.pdf [http://dx.doi.org/10.1016/0167-2789(82)90052-5] |
| [2] | L. Ingber, "Statistical mechanics of neocortical interactions. dynamics of synaptic modification", Physical Review A, vol. 28, pp. 395-416. Available from: https://www.ingber.com/smni83_dynamics.pdf [http://dx.doi.org/10.1103/PhysRevA.28.395] |
| [3] | L. Ingber, "Statistical mechanics of neocortical interactions. derivation of short-term-memory capacity", Physical Review A, vol. 29, pp. 3346-3358. Available from: https://www.ingber.com/smni84_stm.pdf [http://dx.doi.org/10.1103/PhysRevA.29.3346] |
| [4] | L. Ingber, "Statistical mechanics of neocortical interactions: Stability and duration of the 7+/-2 rule of short-term-memory capacity", Physical Review A, vol. 31, no. 2, pp. 1183-1186. Available from: https://www.ingber.com/smni85_stm.pdf [http://dx.doi.org/10.1103/PhysRevA.31.1183] [PMID: 9895606] |
| [5] | L. Ingber, "Statistical mechanics of neocortical interactions: Path-integral evolution of short-term memory", Physical Review E, vol. 49, no. 5, pp. 4652-4664. Available from: https://www.ingber.com/smni94_stm.pdf [http://dx.doi.org/10.1103/PhysRevE.49.4652] [PMID: 9961760] |
| [6] | L. Ingber, “Columnar EEG magnetic influences on molecular development of short-term memory,” In: Short-Term Memory: New Research, G. Kalivas and S. Petralia, Eds., NY: Nova, 2012, pp. 37-72. Available from: https://www.ingber.com/smni11_stm_scales.pdf |
| [7] | W. Hick, "On the rate of gains of information", Quarterly Journal Experimental Psychology, vol. 34, no. 4, pp. 1-33. |
| [8] | L. Ingber, "Statistical mechanics of neocortical interactions: Reaction time correlates of the g factor", Psycholoquy, vol. 10, no. 068, . Invited commentary on The g Factor: The Science of Mental Ability by Arthur Jensen. Available from: https://www.ingber.com/ smni99_g_factor.pdf |
| [9] | A. Jensen, Individual differences in the hick paradigm.Speed of Information-Processing and Intelligence., Ablex: Norwood, NJ, pp. 101-175. |
| [10] | L. Ingber, "Statistical mechanics of neocortical interactions: Applications of canonical momenta indicators to electroencephalography", Physical Review E, vol. 55, no. 4, pp. 4578-4593. Available from: https://www.ingber.com/smni97_cmi.pdf [http://dx.doi.org/10.1103/PhysRevE.55.4578] |
| [11] | L. Ingber, "Influence of macrocolumnar EEG on ca waves", Current Progress Journal, vol. 1, no. 1, pp. 4-8. Available from: https://www.ingber.com/smni12_vectpot.pdf [http://dx.doi.org/10.2139/ssrn.2091676] |
| [12] | L. Ingber, Calculating consciousness correlates at multiple scales of neocortical interactions,” in Horizons in Neuroscience Research, A. Costa and E. Villalba, Eds., NY: Nova, 2015, pp. 153-186, ISBN: 978-1-63482-632-7 Available from: https://www.ingber.com/ smni15_calc_conscious.pdf |
| [13] | L. Ingber, "Statistical mechanics of neocortical interactions: Large-scale EEG influences on molecular processes", Journal of Theoretical Biology, vol. 395, pp. 144-152. Available from: https://www.ingber.com/smni16_large-scale_molecular.pdf [http://dx.doi.org/10.1016/j.jtbi.2016.02.003] [PMID: 26874226] |
| [14] | L. Ingber, "Evolution of regenerative ca-ion wave-packet in neuronal-firing fields: Quantum path-integral with serial shocks", International Journal of Innovative Research in Information Security, vol. 4, no. 2, pp. 14-22. Available from: https://www.ingber.com/ path17_quantum_pathint_shocks.pdf |
| [15] | L. Ingber, M. Pappalepore, and R.R. Stesiak, "Electroencephalographic field influence on calcium momentum waves", Journal of Theoretical Biology, vol. 343, pp. 138-153. Available from: https://www.ingber.com/smni14_EEG_ca.pdf [http://dx.doi.org/10.1016/j.jtbi.2013.11.002] [PMID: 24239957] |
| [16] | P. Nunez, R. Srinivasan, and L. Ingber, Theoretical and experimental electrophysiology in human neocortex: Multiscale correlates of conscious experience.Multiscale Analysis and Nonlinear Dynamics: From genes to the brain., Wiley: New York, pp. 149-178. [http://dx.doi.org/10.1002/9783527671632.ch06] |
| [17] | L. Ingber, "Statistical mechanics of nonlinear nonequilibrium financial markets", Mathematical Modelling, vol. 5, no. 6, pp. 343-361. Available from: https://www.ingber.com/markets84_statmech.pdf [http://dx.doi.org/10.1016/0270-0255(84)90022-8] |
| [18] | L. Ingber, "A simple options training model", Mathematical Computer Modelling, vol. 30, no. 5-6, pp. 167-182. Available from: https://www.ingber.com/markets99_spread.pdf [http://dx.doi.org/10.1016/S0895-7177(99)00155-7] |
| [19] | L. Ingber, "Trading in risk dimensions", G. Gregoriou, Ed., The Handbook of Trading: Strategies for Navigating and Profiting from Currency, Bond, and Stock Markets., McGraw-Hill: New York, pp. 287-300. |
| [20] | L. Ingber, and R. Mondescu, "Optimization of trading physics models of markets", IEEE Transactions Neural Networks, vol. 12, no. 4, pp. 776-790. Available from: https://www.ingber.com/markets01_optim_trading.pdf [http://dx.doi.org/10.1109/72.935091] |
| [21] | L. Ingber, "Automated internet trading based on optimized physics models of markets", Intelligent Internet-Based Information Processing Systems, .https://www.ingber.com/markets03_automated.pdf [http://dx.doi.org/10.1142/9789812795342_0009] |
| [22] | L. Ingber, C. Chen, R.P. Mondescu, D. Muzzall, and M. Renedo, "Probability tree algorithm for general diffusion processes", Physical Review E, vol. 64, no. 5 Pt 2, p. 056702. Available from: https://www.ingber.com/path01_pathtree.pdf [http://dx.doi.org/10.1103/PhysRevE.64.056702] [PMID: 11736136] |
| [23] | L. Ingber, "High-resolution path-integral development of financial options", Physica A, vol. 283, no. 3-4, pp. 529-558. Available from: https://www.ingber.com/markets00_highres.pdf [http://dx.doi.org/10.1016/S0378-4371(00)00229-6] |
| [24] | L. Ingber, and J. Wilson, "Volatility of volatility of financial markets", Mathematical Computer Modelling, vol. 29, no. 5, pp. 39-57. Available from: https://www.ingber.com/markets99_vol.pdf [http://dx.doi.org/10.1016/S0895-7177(99)00048-5] |
| [25] | S. Aaronson, and P. Christiano, “Quantum money from hidden subspaces,” MIT, Cambridge, MA, Techincal Report arXiv:1203.4740 [quant-ph], 2012. [http://dx.doi.org/10.1145/2213977.2213983] |
| [26] | L. Accardi, and A. Boukas, “The quantum black-scholes equation,” U di Roma Torvergata, Rome, Techincal Report arXiv:0706.1300 [q-fin.PR], 2007. |
| [27] | B. Baaquie, C. Coriano, and M. Srikant, “Quantum mechanics, path integrals and option pricing: Reducing the complexity of finance,” National University Singapore, Singapore, Techincal Report arXiv:cond-mat/0208191 [cond-mat.soft], 2002. |
| [28] | J. Jogenfors, “Quantum bitcoin: An anonymous and distributed currency secured by the no-cloning theorem of quantum mechanics,” Linkoping U, Linkoping, Sweden, Techincal Report arXiv:1604.01383 [quant-ph], 2016. |
| [29] | K. Meyer, “Extending and simulating the quantum binomial options pricing model,” U Manitoba, Winnipeg, Canada, Techincal Report Thesis, 2009. Available from: http://hdl.handle.net/1993/3154 |
| [30] | E. Piotrowski, M. Schroeder, and A. Zambrzycka, "Quantum extension of European option pricing based on the Ornstein-Uhlenbeck process", Physica A, vol. 368, no. 1, pp. 176-182. [http://dx.doi.org/10.1016/j.physa.2005.12.021] |
| [31] | L. Ingber, "Options on quantum money: Quantum path-integral with serial shocks", International Journal of Innovative Research in Information Security, vol. 4, no. 2, pp. 7-13. Available from: https://www.ingber.com/path17_quantum_options_shocks.pdf |
| [32] | F. Langouche, D. Roekaerts, and E. Tirapegui, Functional Integration and Semiclassical Expansions., D. Reidel: Dordrecht, The Netherlands, . [http://dx.doi.org/10.1007/978-94-017-1634-5] |
| [33] | L. Schulman, Techniques and Applications of Path Integration., J. Wiley and Sons: New York, . |
| [34] | L. Ingber, "Statistical-mechanical aids to calculating term-structure models", Physical Review A, vol. 42, no. 12, pp. 7057-7064. Available from: https://www.ingber.com/markets90_interest.pdf [http://dx.doi.org/10.1103/PhysRevA.42.7057] [PMID: 9904019] |
| [35] | M. Wehner, and W. Wolfer, "Numerical evaluation of path-integral solutions to Fokker-Planck equations. I", Physical Review A, vol. 27, pp. 2663-2670. [http://dx.doi.org/10.1103/PhysRevA.27.2663] |
| [36] | L. Ingber, and P.L. Nunez, "Statistical mechanics of neocortical interactions: High-resolution path-integral calculation of short-term memory", Physical Review E, vol. 51, no. 5, pp. 5074-5083. Available from: https://www.ingber.com/smni95_stm.pdf [http://dx.doi.org/10.1103/PhysRevE.51.5074] [PMID: 9963220] |
| [37] | L. Ingber, R. Srinivasan, and P. Nunez, "Path-integral evolution of chaos embedded in noise: Duffing neocortical analog", Mathematical Computer Modelling, vol. 23, no. 3, pp. 43-53. Available from: https://www.ingber.com/path96_duffing.pdf [http://dx.doi.org/10.1016/0895-7177(95)00232-4] |
| [38] | M. Wehner, and W. Wolfer, "Numerical evaluation of path-integral solutions to Fokker-Planck equations. II. restricted stochastic processes", Physical Review A, vol. 28, pp. 3003-3011. [http://dx.doi.org/10.1103/PhysRevA.28.3003] |
| [39] | M.F. Wehner, and W.G. Wolfer, "Numerical evaluation of path-integral solutions to Fokker-Planck equations. III. Time and functionally dependent coefficients", Physical Review A, vol. 35, no. 4, pp. 1795-1801. [http://dx.doi.org/10.1103/PhysRevA.35.1795] [PMID: 9898343] |
| [40] | L. Ingber, H. Fujio, and M. Wehner, "Mathematical comparison of combat computer models to exercise data", Mathematical Computer Modelling, vol. 15, no. 1, pp. 65-90. Available from: https://www.ingber.com/combat91_data.pdf [http://dx.doi.org/10.1016/0895-7177(91)90017-2] |
| [41] | L. Ingber, "Path-integral quantum PATHTREE and PATHINT algorithms", International Journal of Innovative Research in Information Security, vol. 3, no. 5, pp. 1-15. Available from: https://www.ingber.com/path16_quantum_path.pdf |
| [42] | M. O’Callaghan, and B.N. Miller, "Path integral Monte Carlo on a lattice: extended states", Physical Review E, vol. 89, no. 4, p. 042124. [http://dx.doi.org/10.1103/PhysRevE.89.042124] [PMID: 24827210] |
| [43] | L. Ingber, “Adaptive simulated annealing (ASA),” Caltech Alumni Association, Pasadena, CA, Technical Report, Global optimization C-code, 1993. Available from: https://www.ingber.com/#ASA-CODE |
| [44] | J. Hull, Options, Futures, and Other Derivatives., 4th edPrentice Hall: Upper Saddle River, NJ, . |
| [45] | L. Ingber, “Computational algorithms derived from multiple scales of neocortical processing,” In: Pointing at Boundaries: Integrating Computation and Cognition on Biological Grounds, A. Pereira, E. Massad, and N. Bobbitt, Eds., Springer: New York, 2011, pp. 1-13. Invited Paper. Available from: https://www.ingber.com/smni11_cog_comp.pdf |
| [46] | S. Murakami, and Y. Okada, "Contributions of principal neocortical neurons to magnetoencephalography and electroencephalography signals", Journal of Physiology, vol. 575, no. Pt 3, pp. 925-936. [http://dx.doi.org/10.1113/jphysiol.2006.105379] [PMID: 16613883] |
| [47] | P. Nunez, and R. Srinivasan, Electric Fields of the Brain: The Neurophysics of EEG., 2nd edOxford University Press: London, . [http://dx.doi.org/10.1093/acprof:oso/9780195050387.001.0001] |
| [48] | P. Facchi, D. Lidar, and S. Pascazio, "Unification of dynamical decoupling and the quantum Zeno effect", Physical Review A, vol. 69, no. 032314, pp. 1-6. |
| [49] | P. Facchi, and S. Pascazio, "Quantum Zeno dynamics: mathematical and physical aspects", Journal of Physics A, vol. 41, no. 493001, pp. 1-45. |
| [50] | G. Giacosa, and G. Pagliara, "Quantum Zeno effect by general measurements", Physical Review A, vol. 052107, pp. 1-5. |
| [51] | W. Kozlowski, S. Caballero-Benitez, and I. Mekhov, “Non-hermitian dynamics in the quantum Zeno limit,” University Oxford, Oxford, UK, Technical Report, arXiv:1510.04857 [quant-ph], 2015. |
| [52] | M. Muller, S. Gherardini, and F. Caruso, “Quantum Zeno dynamics through stochastic protocols,” University Florence, Florence, Italy, Technical Report, arXiv:1607.08871v1 [quant-ph], 2016. |
| [53] | Y.S. Patil, S. Chakram, and M. Vengalattore, "Measurement-induced localization of an ultracold lattice gas", Physical Review Letters, vol. 115, no. 14, p. 140402. Available from: http://link.aps.org/doi/10.1103/PhysRevLett.115.140402 [http://dx.doi.org/10.1103/PhysRevLett.115.140402] [PMID: 26551797] |
| [54] | S. Wu, L. Wang, and X. Yi, "Time-dependent decoherence-free subspace", Journal of Physics A, vol. 405305, pp. 1-11. |
| [55] | P. Zhang, Q. Ai, Y. Li, D. Xu, and C. Sun, "Dynamics of quantum Zeno and anti-Zeno effects in an open system", Science China Physics, Mechanics and Astronomy, vol. 57, no. 2, pp. 194-207. [http://dx.doi.org/10.1007/s11433-013-5377-x] |
| [56] | J. Preskill, "Quantum mechanics,” Caltech, Pasadena, CA, Technical Report, Lecture Notes, 2015", Available from: http://www.theory.caltech.edu/people/preskill/ph219/ |
| [57] | J. Conway, and S. Kochen, “The free will theorem,” Princeton U, Princeton, NJ, Technical Report, arXiv:quant-ph/0604079 [quant-ph], 2006. [http://dx.doi.org/10.1007/s10701-006-9068-6] |
| [58] | J. Conway, and S. Kochen, "The strong free will theorem", Notices of the American Mathematical Society, vol. 56, no. 2, pp. 226-232. |
| [59] | S. Dehaene, H. Lau, and S. Kouider, "What is consciousness, and could machines have it?", Science, vol. 358, no. 6362, pp. 486-492. [http://dx.doi.org/10.1126/science.aan8871] [PMID: 29074769] |
| [60] | L. Ingber, "Towards a unified brain theory", Journal Social Biological Structures, vol. 4, pp. 211-224. Available from: https://www.ingber.com/smni81_unified.pdf [http://dx.doi.org/10.1016/S0140-1750(81)80037-1] |
| [61] | J. Asher, "Brain’s code for visual working memory deciphered in monkeys NIH-funded study,” NIH, Bethesda, MD, Technical Report, NIH Press Release, 2012", Available from: http://www.nimh.nih.gov/news/ science-news/2012/in-sync-brain-waves-hold-memory-of-objects-just-seen.shtml |
| [62] | R.F. Salazar, N.M. Dotson, S.L. Bressler, and C.M. Gray, "Content-specific fronto-parietal synchronization during visual working memory", Science, vol. 338, no. 6110, pp. 1097-1100. [http://dx.doi.org/10.1126/science.1224000] [PMID: 23118014] |
| [63] | A. Pouget, J.M. Beck, W.J. Ma, and P.E. Latham, "Probabilistic brains: knowns and unknowns", Nature Neuroscience, vol. 16, no. 9, pp. 1170-1178. [http://dx.doi.org/10.1038/nn.3495] [PMID: 23955561] |
| [64] | K.A. Ericsson, and W.G. Chase, "Exceptional memory", American Scientist, vol. 70, no. 6, pp. 607-615. [PMID: 7181217] |
| [65] | G.J. Zhang, and H.A. Simon, "STM capacity for Chinese words and idioms: chunking and acoustical loop hypotheses", Memory and Cognition, vol. 13, no. 3, pp. 193-201. [http://dx.doi.org/10.3758/BF03197681] [PMID: 4046819] |
| [66] | F. Black, and M. Scholes, "The pricing of options and corporate liabilities", The Journal of Political Economy, vol. 81, pp. 637-659. [http://dx.doi.org/10.1086/260062] |
| [67] | B. Balaji, "Option pricing formulas and nonlinear filtering: a Feynman path integral perspective", Signal Processing, Sensor Fusion, and Target Recognition XXII, vol. 8745, pp. 1-10. [http://dx.doi.org/10.1117/12.2017901] |
| [68] | L. Ingber, Adaptive simulated annealing.Stochastic global optimization and its applications with fuzzy adaptive simulated annealing., Springer: New York, pp. 33-61. Available from: https://www.ingber.com/asa11_options.pdf.. |



