- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Cybernetics & Systemics Journal
(Discontinued)
ISSN: 1874-110X ― Volume 12, 2018
Research on a Decision-making Model for Service Restoration in a Smart Distribution Network
Jiahang Yuan*, Cunbin Li
Abstract
In order to restore power to out-of-service areas quickly, this paper proposes a new service restoration decision-making algorithm for a distribution network. First, using heuristic rules, a candidate service restoration scheme set is generated. Considering the target of service restoration, five evaluation indices are introduced, including the quantities of restored load and transferred load, the margin of load capacity, the rate of load balancing, and the switching times of circuit breakers. Second, because of the problem of fuzzy measure identification, interaction between attributes, and the requirements for consistency with group decision making, this study defines the Shapley value identification method based on the Mahalanobis-Taguchi system and interval fuzzy preference relations. The fuzzy measure is obtained by the Shapley value, and the decision-making model is constructed by the Choquet integral with φs transformation function. Finally, an example application proves that the method is feasible and effective for decision making. Compared with the other method, the results verify the superiority of the decision process and show that it is consistent with the real conditions of post-fault restoration in a smart distribution network.
Article Information
Identifiers and Pagination:
Year: 2017Volume: 11
First Page: 44
Last Page: 57
Publisher Id: TOCSJ-11-44
DOI: 10.2174/1874110X01711010044
Article History:
Received Date: 01/10/2016Revision Received Date: 28/10/2016
Acceptance Date: 16/12/2016
Electronic publication date: 28/02/2017
Collection year: 2017
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: (https://creativecommons.org/licenses/by/4.0/legalcode). This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
* Address correspondence to this author at the School of Economics and Management, North China Electric Power University, Beinong Road 2, Changping District, Beijing, China; Tel: +8615810434877; E-mail: yuanjiahang@126.com
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 01-10-2016 |
Original Manuscript | Research on a Decision-making Model for Service Restoration in a Smart Distribution Network | |
1. INTRODUCTION
As a future development trend, smart grids emphasize a distribution network’s ability to self-heal. Because a distribution network is user-oriented, the strength of its self-healing ability directly affects the safety and reliability of its power supply as well as economic reliability. Service restoration refers to the idea that when a fault occurs, some restoration strategies are implemented on the basis of fault location and fault isolation; these strategies operate on feeder network switches and disconnect switches, transfer the power load to other feeders, and find the best path to restore power promptly to the non-fault zones [1L. Liu, X.F. Chen, and D.H. Zhai, "Status and prospect of service restoration in smart distribution network", Power System Protection and Control, vol. 39, pp. 149-154, 2011.]. Service restoration in a distribution network is a multi-objective optimization problem with constraints. The problem has been addressed with methods that are roughly divided into three categories: mathematical optimization, artificial intelligence algorithms, and heuristic search algorithms. The mathematical optimization approach adopts methods such as integer programming and score delimitation by setting an objective function, which is suitable for fault problems in a less complex power distribution system; however, mathematical optimization is subject to dimension errors [2S.P. Singh, G.S. Raju, and G.K. Rao, "A heuristic method for feeder reconfiguration and service restoration in distribution network", International Journal of Electrical Power and Energy Systems, vol. 31, pp. 309-314, 2009.
[http://dx.doi.org/10.1016/j.ijepes.2009.03.013] ]. Artificial intelligence has a strong advantage in solving faults in complex systems. However, because of the large amount of calculations and iterations, and its tendency to focus on local optima, artificial intelligence has no strength in processing speed and practicality. The heuristic search algorithm converts experts’ knowledge and the experience into processing rules, and provides an optimal restoration scheme immediately. Such a process greatly reduces the interruption time of a fault load with a strong response. Hence, this paper selects heuristic rules to generate a service restoration scheme in a distribution network. Researchers typically combine heuristic rules with other methods. In Zhang et al. [3H.B. Zhang, X.Y. Zhang, and W.W. Tao, "A breadth-first search based service restoration algorithm for distribution network", Power System Technology, vol. 34, pp. 103-108, 2010.], a reserve capacity correction coefficient is introduced, and a breadth-first search algorithm is used to restore power to out-of-service areas. In Zhou et al. [4Y.Y. Zhou, Q. Zhou, Y.M. Liu, Z.S. Yang, C.X. Sun, and Y. Dai, "Heuristic research and fuzzy evaluation for-post-fault restoration in distribution network", Journal of Chongqing University, vol. 33, pp. 78-82, 2010.], the actual difficulty of the switching operations and the priority of restoring power are considered, four restoration schemes are formed, and a fuzzy evaluation method is used to make decisions. In Zang et al. [5T.L. Zang, J.C. Zhong, Z.Y. He, and Q.Q. Qian, "Service restoration of distribution network based on heuristic rules and entropy weight", Power System Technology, vol. 36, pp. 251-257, 2012.], five evaluation indices are established on the basis of heuristic rules; at the same time, subjective and objective weights are taken into account. In Zang et al. [6T.L. Zang, Z.Y. He, D.Y. Ye, J.W. Yang, and Q.Q. Qian, "Distribution network service restoration based on interval number grey relation decision-making considering load change", Power System Protection and Control, vol. 41, pp. 38-43, 2013.], a single number of the initial decision matrix is extended to an interval on the basis of Zang et al. [5T.L. Zang, J.C. Zhong, Z.Y. He, and Q.Q. Qian, "Service restoration of distribution network based on heuristic rules and entropy weight", Power System Technology, vol. 36, pp. 251-257, 2012.], grey correlation analysis is utilized to evaluate candidate schemes, and the choice service restoration scheme is effectively solved for various load conditions. However, these studies suffer from a number of shortcomings: First, the evaluation index weight is given by only one expert directly, which could result in a greater bias and a failure to choose the optimal solution. Second, these studies ignore the interaction among the index attributes. For example, the correlation of the first index and the fourth index reached a value of −0.8572, which means there was an overlap of information between attributes. If the overlapping information cannot be eliminated, the operation results will be distorted.
The Choquet integral is a nonlinear function defined on the basis of fuzzy measure by Grabisch, it can effectively deal with strong correlations among the indices, and thus it has been widely used in various types of evaluations, decisions, and assessment issues [7D.Y. Shi, G.J. Xiong, J.F. Chen, and Y.H. Li, "Divisional fault diagnosis of power grids based on RBF neural network and choquet integral fusion", Proceedings of the CSEE, vol. 34, pp. 562-569, 2014.-11J.Z. Wu, S.L. Yang, Q. Zhang, and S. Ding, "2-additive Capacity Identification Methods from Multicriteria Correlation Preference Information", IEEE Transactions on Fuzzy Systems, vol. 23, pp. 2094-2106, 2015.
[http://dx.doi.org/10.1109/TFUZZ.2015.2403851] ]. But the basic premise of applying Choquet integral is obtaining the fuzzy measure which describes the interactions between attributes. The fuzzy measure has the non-additive property, which is different from classical measures [12Z.P. Chang, and L.S. Cheng, "Multi-attribute decision making method based on Mahalanobis-Taguchi System and Fuzzy Integral", Journal of Industrial Engineering, vol. 29, no. 3, pp. 107-115, 2015.]. When there are n attributes, we need to calculate 2n-2 parameters to make sure the fuzzy measures of all attributes and subsets. So there will be huge amount of computation. In roder to reduce the numbers of parameters, Sugeno proposed λ fuzzy measure which only need to calculate attributes’ fuzzy measures so that we could obtain all decision-making attributes set’s fuzzy measures. So far, there are two categories to obtain λ fuzzy measure. One is subjective assignment, the other is objective assignment including ant algorithm, neural network and so on. Subjective assignment methods rely heavily on human’s recogintion and objective assignment methods usually need lots of sample data and too comlicated to apply on heuristic search algorithms with limited alternatives.
In Chang and Cheng [13Z.P. Chang, and L.S. Cheng, "Choquet integral multi-attribute decision making method based on Mahalanobis-Taguchi system and φs transformation", Systems Engineering and Electronics, vol. 35, pp. 1702-1710, 2013.], the researchers explore the method of the Choquet integral with ϕs transformation, based on using the Shapley value instead of index weights to determine the λ fuzzy measure proposed in Chang and Cheng [14Z.P. Chang, and L.S. Cheng, "Grey fuzzy integral correlation degree decision model based on Mahalanobis-Taguchi Gram-Schmidt and φs transformation", Control and Decision, vol. 29, pp. 1257-1261, 2014.]. Meanwhile, the Mahalanobis-Taguchi system is used in the measurement method to determine the Shapley value and a reasonable analysis is made in E. Takahagi [15E. Takahagi, "On identification methods of fuzzy measures using weights and λ", Japanese Journal of Fuzzy Sets and System, vol. 12, pp. 665-676, 2000.]. The Mahalanobis-Taguchi system can eliminate the interaction between the index attributes, and is an effective method to determine the objectives along with the overall importance of the attributes. Nevertheless, in the heuristic rules, the subjective knowledge and experience of experts will affect decision making, and taking advantage of the Mahalanobis-Taguchi system to identify the Shapley value alone does not conform to the research objectives of the present.
Hence, this study identifies the Shapley value by adopting a combination of subjective and objective methods. There are many methods for obtaining subjective weights, such as the analytic hierarchy process (AHP), analytic network process (ANP), and expert scoring method. In contrast with some of the group decision-making methods, a preference relation based on two alternatives compared to each other can better express the preferences of the policymakers. To sum up, this paper presents a new approach to decision making. First, the proposed approach takes advantage of interval fuzzy preference relations and consistency matrices to determine subjective weights that experts have set iteratively, and then uses the Mahalanobis-Taguchi system to construct an optimization model for obtaining the overall importance of the attributes, which is called objective weight. Second, this method calculates the Shapley value on the basis of subjective and objective weights, and then finds the fuzzy measure. Finally, the Choquet integral value of each scheme is calculated by custom values of λ to select the optimal solution.
2. SERVICE RESTORATION GOALS IN DISTRIBUTION NETWORK AND EVALUATION INDICES
The primary service restoration goals for a distribution network are:
- Avoid service interruption to important loads.
- After restoration, minimize network loss in the entire process.
- Reduce the loss of power loads.
- Balance load distribution.
- Avoid overload.
- Reduce the amount of work during the restoration process and minimize the impact on fault-free areas.
In order to realize the service restoration goals in a distribution network, cite the index in [5T.L. Zang, J.C. Zhong, Z.Y. He, and Q.Q. Qian, "Service restoration of distribution network based on heuristic rules and entropy weight", Power System Technology, vol. 36, pp. 251-257, 2012.] as an evaluation standard of the restoration scheme.
The quantities of a restored load. Service restoration scheme in a distribution network can make the fault-free feeder loading, partial power is out-of-service but the power of service areas can normally supply. The quantities of a restored load are known as the sum of the load quantity of restoration, the unit of which is Ampere.
The margin of feeder load capacity. The difference between the rated load and the actual load is the margin of feeder load capacity, which represents the resilience of the distribution network when encountering again. There is a positive correlation between the index and the resilience, that is to say, the greater the margin, the stronger the restoration. After the implementation of an actual restoration scheme, the margin values of feeder load capacity are different. This paper adopts the minimum value as the evaluation index, the unit of which is Ampere.
Switching times of circuit breakers. In the process of restoration, there is a need for the operation of the switch - on or off. Each operation means that the cost of restoration will increase accordingly. The index shows the cost of the action.
Transferred load. The acceptable transferred load on one feeder is called feeder transferred load. Similar to the margin of feeder load capacity, the transferred load of each feeder is different as well. This paper selects the maximum load current increment of each feeder as an evaluation index after the implementation of a restoration scheme. The smaller the transferred load caused by a service restoration scheme, the smaller influence on the original lines running. Its unit is Ampere.
Rate of load balancing. We define rate of load balancing as the maximum of which among all switches. It indicates the load balancing extent of the distribution network. When its value gets smaller, the smaller network loss will be and more conducive to economic operating of the distribution network.
3. THEORETICAL INTRODUCTION AND ANALYSIS
3.1. Mahalanobis-Taguchi System
Suppose there are n index attributes {x1,x2,...,xn}, and Y=[yk(xi)]l×n is the sample data matrix. The mean u(xi) and standard deviations s(xi) of attributes xi can be calculated from:
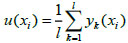 |
(1) |
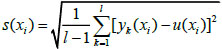 |
(2) |
When the type of index is cost, let z(xi)=-1×z(xi). Standardize Y=[yk(xi)]l×n by using (1) and (2) as follows:
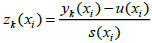 |
(3) |
Z=[yk(xi)]l×n is the standardized sample data. If the importance of any attribute subset is needed, all subsets of the attributes must be identified first. When X′={x1,x2}, let 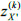 be the k-th sample data of X′, and then
be the k-th sample data of X′, and then 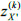 ={z(x1), z(x2)}.
={z(x1), z(x2)}.
Select two kinds of samples with obvious distinguishable differences from Z=[yk(xi)]l×n, one is a positive ideal solution and the other is a negative ideal solution in normal.
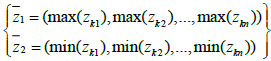 |
(4) |
Calculate the Mahalanobis distance between each subset and the two kinds of samples with obvious distinguishable differences by:
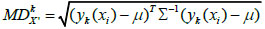 |
(5) |
∑ represents a covariance matrix. ∑=diag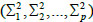 if the correlation between multidimensional attributes is eliminated, where
if the correlation between multidimensional attributes is eliminated, where 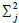 is the variance of the overall sample XA’s j-th attribute. When ∑ is singular, then MD(x)=
is the variance of the overall sample XA’s j-th attribute. When ∑ is singular, then MD(x)=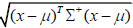 , where the pseudo-inverse of ∑ is ∑+=UTV-1U, V is the r×r diagonal matrix composed by the nonzero eigenvalue of ∑ and r is the rank of ∑. U is the r×p diagonal matrix composed by the eigenvectors corresponding to eigenvalues in ∑.
, where the pseudo-inverse of ∑ is ∑+=UTV-1U, V is the r×r diagonal matrix composed by the nonzero eigenvalue of ∑ and r is the rank of ∑. U is the r×p diagonal matrix composed by the eigenvectors corresponding to eigenvalues in ∑.
This study selects the “larger the better” method to calculate the importance of attributes in the classification by:
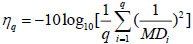 |
(6) |
3.2. Choquet Integral and Shapley Value
Definition 1 [16M. Sugeno, “Fuzzy Measure and Fuzzy Integrals, A Survey”, Fuzzy Automata and Decision Processes., North-Holland: New York, 1997.]: Suppose X={xk|k=1,2,...,n} is a finite set, P(X)is the power set of X, (X,P(X)) is a space, and g: P(X)→[0,1] is a group of set functions. If the following conditions are met:
● g(ø)=0,g(X)=1
● 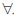 A,B
A,B 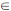 P (X), if A
P (X), if A B, then g(A) ≤ g(B)
B, then g(A) ≤ g(B)
then define g as a fuzzy measure function, if it still meets with the condition 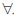 A,B
A,B 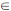 P (X), A
P (X), A 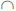 B= Ø, and λ > -1 then:
B= Ø, and λ > -1 then:
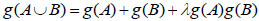 |
(7) |
and define g as a fuzzy measure function of λ, where λ indicates the degree of interaction between attributes.
Definition 2: Suppose X={x1, x2,...xn} is a discrete attribute set, g is fuzzy measure function of (X,P(X)), and the discrete Choquet integral of f:X →R+ on fuzzy measure g is represented as follows:
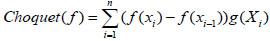 |
(8) |
where i indicates the subscript of ranked f (x1)≤...f (xn). Let f (xO)=0, Xi={xi, xi+1,...,xn}.
The Choquet integral based on fuzzy measure breaks through the limitation of the linear fusion and meets the requirement of the evaluation for a service restoration scheme in a distribution network. f (xi) can be the index attribute value or utility function. The Choquet integral is a comprehensive evaluation value of each scheme as an aggregation operator.
Definition 3 [17Y. Tukamoto, "A measure theoretic approach to evaluation of fuzzy set defined on probability space", Journal of Fuzzy Mathematics, vol. 2, no. 3, pp. 89-98, 1982.]: When
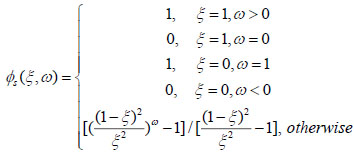 |
(9) |
define øs:[0,1]×[0,1]→[0,1] as the øs transformation. Then the λ fuzzy measure of attribute set X is represented by:
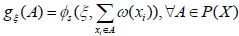 |
(10) |
where ξ = 1 / 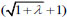 is the attribute interaction degree of X, ω(xi) is the weight of xi, and ξ
is the attribute interaction degree of X, ω(xi) is the weight of xi, and ξ 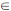 [0,...,0.5,...,1], the value of λ correspondingly is λ
[0,...,0.5,...,1], the value of λ correspondingly is λ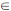 [+ ∞,...,0,...,-1]. Figs. (1
[+ ∞,...,0,...,-1]. Figs. (1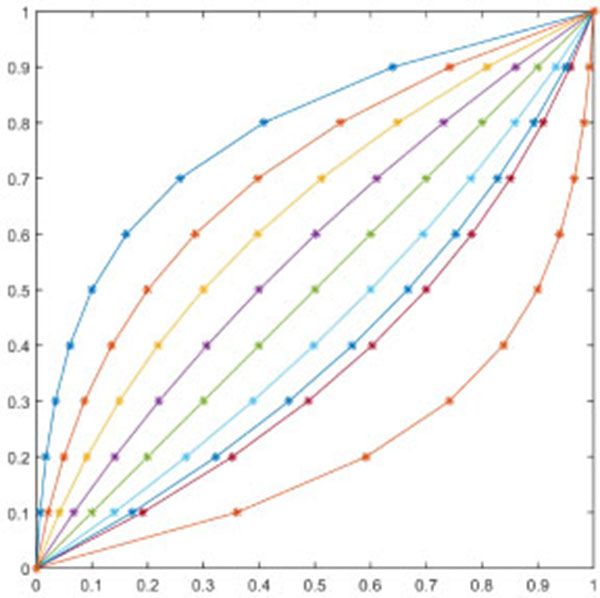 and 2
and 2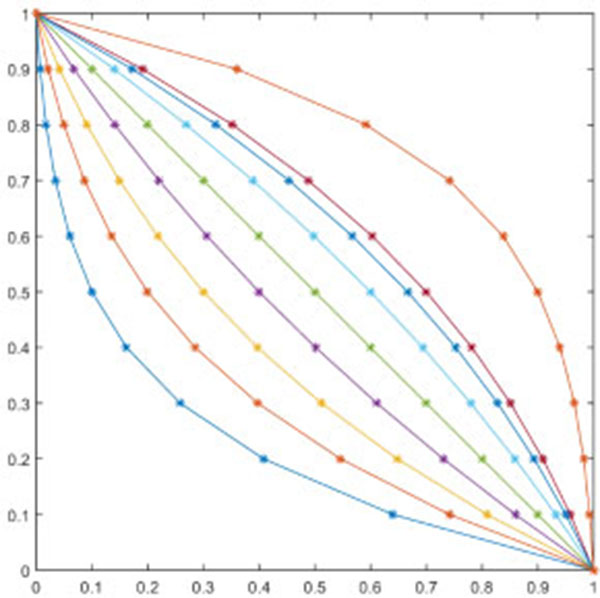 ) show the function øs (ξ,ω) and inverse function
) show the function øs (ξ,ω) and inverse function 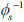 (ξ,ω), respectively.
(ξ,ω), respectively.
In Fig. (1 ), the curves respectively represent function images when ξ ranges from 0.1 to 0.9. On the contrary, the curves in Fig. (2
), the curves respectively represent function images when ξ ranges from 0.1 to 0.9. On the contrary, the curves in Fig. (2 ) respectively represent images when øs ranges from 0.9 to 0.1. Fig. (2
) respectively represent images when øs ranges from 0.9 to 0.1. Fig. (2 ) shows that ω(xk)=
) shows that ω(xk)= 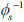 (ξ,ω) is the inverse function of interaction degree ξ. The fuzzy measure formula (10) can be rewritten as:
(ξ,ω) is the inverse function of interaction degree ξ. The fuzzy measure formula (10) can be rewritten as:
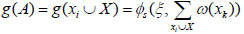 |
(11) |
ξ is the interaction degree of attributes in the decision matrix, as well as the interaction degree between xi and X. If λ is calculated by (10), ω (xk) should be a decreasing function of ξ, which is the interaction degree between xi and X. Considering the independence of attributes, there is no function relationship between ω (xk) and ξ. Referencing the viewpoint in Chang and Cheng [14Z.P. Chang, and L.S. Cheng, "Grey fuzzy integral correlation degree decision model based on Mahalanobis-Taguchi Gram-Schmidt and φs transformation", Control and Decision, vol. 29, pp. 1257-1261, 2014.], the Shapley value of each attribute xi can be used in place of ω (xk), because it is a decreasing function between the Shapley value of fuzzy measure on each attribute xi and ξ.
Definition 4 [18M. Grabisch, "The representation of importance and interaction of features by fuzzy measures", Pattern Recognition, vol. 17, no. 6, pp. 567-575, 1996.
[http://dx.doi.org/10.1016/0167-8655(96)00020-7] ]: g is the fuzzy measure on finite set X, and the Shapley value of each attribute xi on fuzzy measure g is represented by:
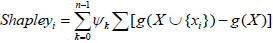 |
(12) |
 |
Fig. (1) Function curve of ϕs (ξ , ω). |
 |
Fig. (2) Function curve of 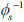 (ξ , ω). (ξ , ω).
|
where Ψk=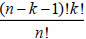 . Shapleyi is based on X, and therefore shows the overall importance of a single attribute. Thus,
. Shapleyi is based on X, and therefore shows the overall importance of a single attribute. Thus, 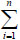 Shapleyi=1.
Shapleyi=1.
Extending (12): 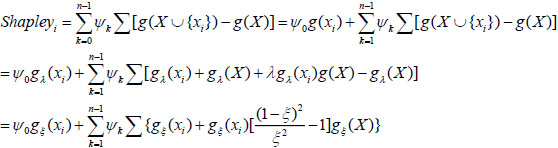
Calculate the derivative of ξ and obtain 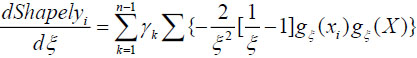 , where 0 < ξ < 1 and
, where 0 < ξ < 1 and 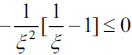 . Because the derivative is less than zero, it is a decreasing function relationship between ξ and Shapleyi. Hence, calculating the fuzzy measure by making use of the Shapley value is more appropriate.
. Because the derivative is less than zero, it is a decreasing function relationship between ξ and Shapleyi. Hence, calculating the fuzzy measure by making use of the Shapley value is more appropriate.
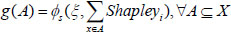 |
(13) |
For the convenience of calculation, (12) is changed to:
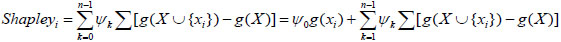 |
(14) |
According to [14Z.P. Chang, and L.S. Cheng, "Grey fuzzy integral correlation degree decision model based on Mahalanobis-Taguchi Gram-Schmidt and φs transformation", Control and Decision, vol. 29, pp. 1257-1261, 2014.], redefine the Shapley value of attribute xi as:
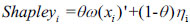 |
where ω(xi)′ is the subjective weight of a group decision that experts have given, θ represents the subjective preference coefficient that the managers of a power grid identified and ni is the overall importance of attributes, which is the objective weight.
The overall importance ni of attribute xi can be solved by an optimization model as follows:
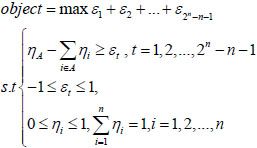 |
(15) |
The value of the objective function will reach a maximum by (15), and the effect of 2n-n-1 attributes in the attribute set will be the largest. The optimal solution of ni not only takes the importance of attributes in decision-making into account, but also considers the ones that are not involved. Therefore, for attribute {x1}, there is a need to calculate n1,2, n1,3, n1,4,...,n1,2,3,...,n1,2,3,4,...,n1,2,3...,n.
The classification function of the Mahalanobis-Taguchi system is to calculate the Mahalanobis distance between data samples, and two kinds of samples with obvious distinguishable differences, as well as to measure the importance by use of signal-to-noise ratio (SNR). It is a kind of covariance distance that cannot be influenced by the number of characteristic variables. Hence, the distance between any attribute and two kinds of samples with obvious distinguishable differences can be obtained; at the same time, the interaction between attributes will be considered. Furthermore, from the calculation formula of SNR, the calculated ni by the Mahalanobis-Taguchi system meets the requirement of monotonicity above. Therefore, it is reasonable to obtain the overall importance of attribute xi by the Mahalanobis-Taguchi system.
3.3. Fuzzy Preference Relations and Consistency Degree
There are numerous calculation methods of subjective weight. When dealing with the results of group decision making, the consistency of the decision-makers must be taken into account. In Chen et al. [19S.M. Chen, S.H. Cheng, and T.E. Lin, "Group decision making systems using group recommendations based on interval fuzzy preference relations and consistency matrices", Information Sciences, vol. 298, pp. 555-567, 2015.
[http://dx.doi.org/10.1016/j.ins.2014.11.027] ], interval fuzzy preference relations and the consistency degree of iterations are adopted to solve subjective weights. Compared to traditional methods, this approach has two advantages: (1) It considers the consistency analysis of an individual and group, so that the consistency is constantly revised and reaches a predefined threshold through an iteration. (2) To ensure the consistency of the collective is higher than that of individuals, it calculates the group collective fuzzy preference relations considering weights by experts.
Definition 5 [20T. Tanino, "Fuzzy preference orderings in group decision making", Fuzzy Sets and Systems, vol. 12, no. 2, pp. 117-131, 1984.
[http://dx.doi.org/10.1016/0165-0114(84)90032-0] ]: Let P be a fuzzy preference relation for the set of alternatives as follows:
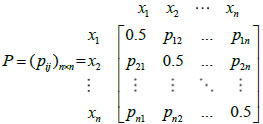 |
(16) |
where X={x1, x2,...,xn} indicates there are n indexes in the decision problem. pij denotes the degree of preference of alternative xi over alternative Xj, pij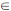 [0,1] and 1 ≤ i ≤ n, 1 ≤ j ≤ n. If pij=0.5, then it represents that there is no difference between alternative xi and alternative Xj; if 0 ≤ pij < 0.5, then it represents that alternative Xj is better than xi, the greater the value of pij, the more important Xj is than xi. The opposite holds if 0.5 < pij ≤ 1. If there exists at least 1 unknown preference value pij in the fuzzy preference relation P= (pij)n×n, which means that the expert does not have a clear idea in selecting the better one between alternative xi and alternative Xj, then P= (pij)n×n is called an incomplete fuzzy preference relation [21E.H. Viedma, S. Alonso, F. Chiclana, and F. Herrera, "A consensus model for group decision making with incomplete fuzzy preference relations", IEEE Transactions on Fuzzy Systems, vol. 15, pp. 863-877, 2007.
[0,1] and 1 ≤ i ≤ n, 1 ≤ j ≤ n. If pij=0.5, then it represents that there is no difference between alternative xi and alternative Xj; if 0 ≤ pij < 0.5, then it represents that alternative Xj is better than xi, the greater the value of pij, the more important Xj is than xi. The opposite holds if 0.5 < pij ≤ 1. If there exists at least 1 unknown preference value pij in the fuzzy preference relation P= (pij)n×n, which means that the expert does not have a clear idea in selecting the better one between alternative xi and alternative Xj, then P= (pij)n×n is called an incomplete fuzzy preference relation [21E.H. Viedma, S. Alonso, F. Chiclana, and F. Herrera, "A consensus model for group decision making with incomplete fuzzy preference relations", IEEE Transactions on Fuzzy Systems, vol. 15, pp. 863-877, 2007.
[http://dx.doi.org/10.1109/TFUZZ.2006.889952] ].
Definition 6: Given a fuzzy preference relation P= (pij)n×n, for any i,j=1,2,...,n, pij + pji = 1 and pii=0.5. The consistency matrix 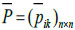 is constructed as [22L.W. Lee, "Group decision making with incomplete fuzzy preference relations based on the additive consistency and the order consistency", Expert Systems with Applications, vol. 39, pp. 11666-11676, 2012.
is constructed as [22L.W. Lee, "Group decision making with incomplete fuzzy preference relations based on the additive consistency and the order consistency", Expert Systems with Applications, vol. 39, pp. 11666-11676, 2012.
[http://dx.doi.org/10.1016/j.eswa.2012.04.043] ]:
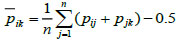 |
(17) |
Definition 7 [23S.M. Chen, T.E. Lin, and L.W. Lee, "Group decision making using incomplete fuzzy preference relations based on the additive consistency and the order consistency", Information Sciences, vol. 259, pp. 1-15, 2014.
[http://dx.doi.org/10.1016/j.ins.2013.08.042] ]: Define the consistency degree between fuzzy preference relation and consistency matrix as:
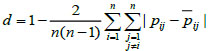 |
(18) |
where d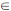 [0,1]; the larger the value of d, the more consistent the fuzzy preference relation.
[0,1]; the larger the value of d, the more consistent the fuzzy preference relation.
Because of the limitations of subjective perception, sometimes it is difficult to provide specific values to express preference relations. However, intervals can exactly express the inherent uncertainty of a preference relation. An interval fuzzy preference relation is a preference relation matrix composed of intervals.
Definition 8 [24Z. Xu, "Consistency of interval fuzzy preference relations in group decision making", Applied Soft Computing, vol. 11, no. 5, pp. 3898-3909, 2011.
[http://dx.doi.org/10.1016/j.asoc.2011.01.019] ]: The interval fuzzy preference relation for the set X of alternatives is:
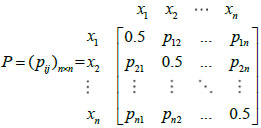 |
(19) |
where 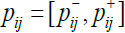 denotes an interval preference value for alternative xi over alternative Xj. Then,
denotes an interval preference value for alternative xi over alternative Xj. Then, 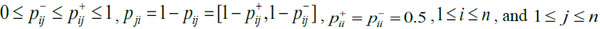 .
.
Definition 9 [25G.L. Xu, and F. Liu, "An approach to group decision making based on interval multiplicative and fuzzy preference relations by using projection", Applied Mathematical Modelling, vol. 37, no. 6, pp. 3929-3943, 2013.
[http://dx.doi.org/10.1016/j.apm.2012.08.007] ]: Suppose A= (aij)n×n and B= (bij)n×n are two interval fuzzy preference relations, where 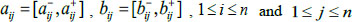 . The relative projection
. The relative projection 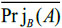 between the two interval fuzzy preference relations is defined as:
between the two interval fuzzy preference relations is defined as:
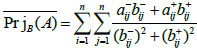 |
(20) |
The closer that the value of 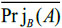 is to 1, the closer the interval fuzzy preference relation A= (aij)n×n is to B= (bij)n×n.
is to 1, the closer the interval fuzzy preference relation A= (aij)n×n is to B= (bij)n×n.
4. Decision-making Model and Steps
Let {A1,...,Al} be all alternative restoration schemes formed according to the distribution network fault, and there are n index attributes corresponding to each of them. Build the initial evaluation matrix 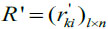 , where 1 ≤ k ≤ l and 1 ≤ i ≤ n. Because of the difference between attributes, there is a need to dimension the index. First, distinguish the type. Second, process the values of benefit type and cost type by (21) and (22). Finally, the standardized decision matrix R= (rki)l×n will be obtained.
, where 1 ≤ k ≤ l and 1 ≤ i ≤ n. Because of the difference between attributes, there is a need to dimension the index. First, distinguish the type. Second, process the values of benefit type and cost type by (21) and (22). Finally, the standardized decision matrix R= (rki)l×n will be obtained.
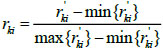 |
(21) |
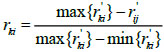 |
(22) |
Assume that there are m interval fuzzy preference relations P1, P2,...,Pm given by m experts {E1, E2,...,Em}, respectively, and assume that there are n alternatives {x1, x2,...,xn}. Pk is shown as 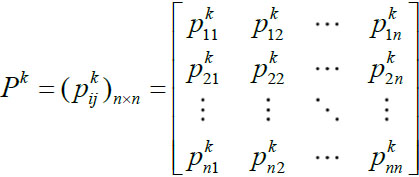 , where
, where 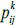 is an interval number, which means xi is better than Xj, as well as
is an interval number, which means xi is better than Xj, as well as 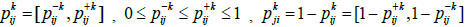 and
and 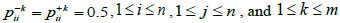 .
.
The decision-making algorithm for service restoration in a distribution network as follows:
Step 1: Let r=0. For the interval fuzzy preference relations Pk given by expert Ek, construct the fuzzy preference relation 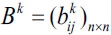 for expert Ek and the collective consistency matrix
for expert Ek and the collective consistency matrix 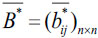 for all experts, and then calculate the consistency degree dk of expert Ek by:
for all experts, and then calculate the consistency degree dk of expert Ek by:
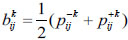 |
(23) |
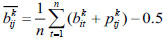 |
(24) |
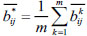 |
(25) |
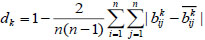 |
(26) |
Step 2: Calculate the weight wk given by experts as:
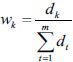 |
(27) |
Step 3: Construct the weighted collective preference relation 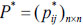 and the group collective preference relation U= (uij)n×n for all experts as:
and the group collective preference relation U= (uij)n×n for all experts as:
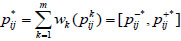 |
(28) |
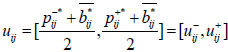 |
(29) |
Step 4: Construct the consistency relation 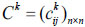 for experts Ek and calculate the group consistency degree CD for all experts by:
for experts Ek and calculate the group consistency degree CD for all experts by:
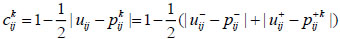 |
(30) |
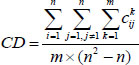 |
(31) |
where λ is a predefined threshold and λ 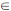 [0,1]. If CD < λ, let r=r+1 and go to Step 5; otherwise, go to Step 7.
[0,1]. If CD < λ, let r=r+1 and go to Step 5; otherwise, go to Step 7.
Step 5: If there exists 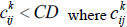 belongs to the consistency relation
belongs to the consistency relation 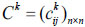 , then modify the initial interval fuzzy preference relation
, then modify the initial interval fuzzy preference relation 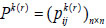 as:
as:
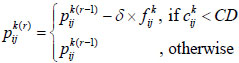 |
(32) |
where δ is a modified constant and 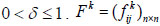 . is the proximity relation for expert Ek shown as:
. is the proximity relation for expert Ek shown as:
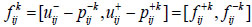 |
(33) |
Step 6: According to the new initial interval preference relation, update 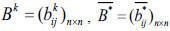 ,
, 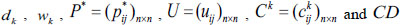 . If CD < γgo to Step 7; otherwise, go back to Step 5.
. If CD < γgo to Step 7; otherwise, go back to Step 5.
Step 7: Calculate the final subjective weight of each index by:
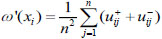 |
(34) |
Step 8: Standardize the decision matrix on the basis of (1) to (4), and determine two kinds of samples with obvious distinguishable differences in the standardized matrix.
Step 9: On the basis of (5) and (6), calculate the Mahalanobis distance between attributes of each subset and two samples respectively: 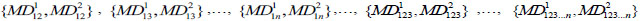 , as well as the SNR of each subset
, as well as the SNR of each subset 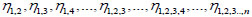 .
.
Step 10: Obtain the overall importance n1,...,nn of set X={x1, x2,...,xn} by the optimization model (15).
Step 11: Calculate Shapley1,...,Shapleyn according to (12), which is the definition of the Shapley value.
Step 12: On the basis of the normalized decision matrix R=(rki)l×n, calculate the Choquet integral comprehensive attribute values of all the schemes Choquet(f) by (10), and rank the results to select the optimal restoration scheme.
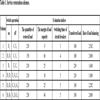
5. EXPERIMENTAL RESULTS
In order to verify the effectiveness of the proposed model, this study references the example and initial data of a complex six-feeder distribution network in [5T.L. Zang, J.C. Zhong, Z.Y. He, and Q.Q. Qian, "Service restoration of distribution network based on heuristic rules and entropy weight", Power System Technology, vol. 36, pp. 251-257, 2012.]. The network diagram is shown in Fig. (3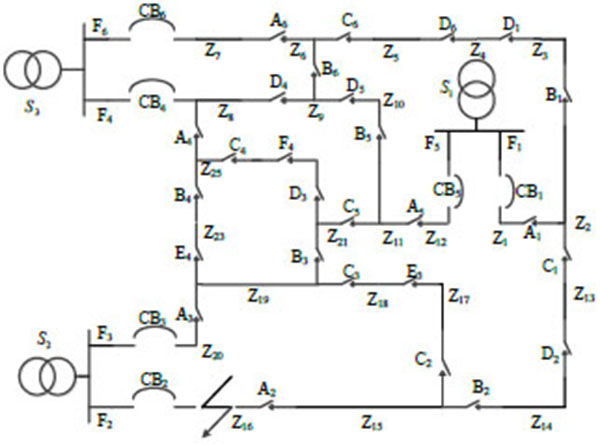 ), where Si is a power supply, CBi is a circuit breaker, Ai, Bi, Ci, Di, Ei and Gi are section switches, Fi is a feeder, and Zi is a power supply area. The switches connected to out-of-service areas are E3 and C1. Closing E3 cannot restore the whole area without cutting off load, and closing C1 can go on districted restoration steps. So the initial alternative is closing E3 and C1, and then open D2. The numbers of switch operation is three. According to only two adjacent feeders in out-of-service areas, the restoration alternatives are formed as follows: two adjacent feeders; one adjacent feeder and one secondary adjacent feeder; two adjacent feeders and one secondary adjacent feeder. Six restoration schemes are formed as shown in Table 1 [5T.L. Zang, J.C. Zhong, Z.Y. He, and Q.Q. Qian, "Service restoration of distribution network based on heuristic rules and entropy weight", Power System Technology, vol. 36, pp. 251-257, 2012.]. Three experts are invited to give preference relations in Table 2. Assume that the predefined threshold value γ=1 and the modified constant δ=0.9. Through step1 to step 7, the subjective weights are calculated. The results are shown in Figs. (4
), where Si is a power supply, CBi is a circuit breaker, Ai, Bi, Ci, Di, Ei and Gi are section switches, Fi is a feeder, and Zi is a power supply area. The switches connected to out-of-service areas are E3 and C1. Closing E3 cannot restore the whole area without cutting off load, and closing C1 can go on districted restoration steps. So the initial alternative is closing E3 and C1, and then open D2. The numbers of switch operation is three. According to only two adjacent feeders in out-of-service areas, the restoration alternatives are formed as follows: two adjacent feeders; one adjacent feeder and one secondary adjacent feeder; two adjacent feeders and one secondary adjacent feeder. Six restoration schemes are formed as shown in Table 1 [5T.L. Zang, J.C. Zhong, Z.Y. He, and Q.Q. Qian, "Service restoration of distribution network based on heuristic rules and entropy weight", Power System Technology, vol. 36, pp. 251-257, 2012.]. Three experts are invited to give preference relations in Table 2. Assume that the predefined threshold value γ=1 and the modified constant δ=0.9. Through step1 to step 7, the subjective weights are calculated. The results are shown in Figs. (4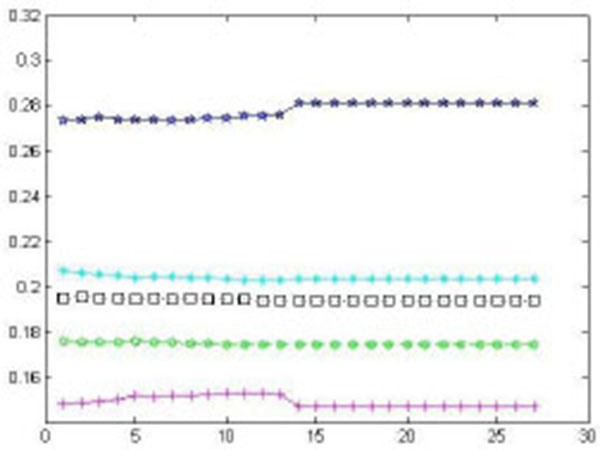 , 5
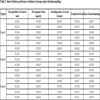
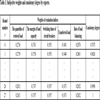
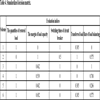
, 5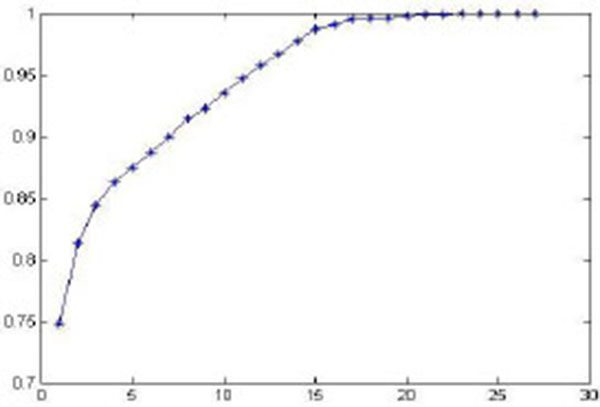 ) and Table 3. Table 4 is the standardized decision matrix which is calculated by step 8. Table 5 shows the correlation coefficient, we can find that the quantities of restored load and transferred load have strong correlation. Through step 9 to step 10, we obtain Mahalanobis distance between two samples, SNR and normalized SNR in Table 6.
) and Table 3. Table 4 is the standardized decision matrix which is calculated by step 8. Table 5 shows the correlation coefficient, we can find that the quantities of restored load and transferred load have strong correlation. Through step 9 to step 10, we obtain Mahalanobis distance between two samples, SNR and normalized SNR in Table 6.
 |
Fig. (3) Network diagram of 6-feeder distribution network. |
 |
Fig. (4) Weights for 27 rounds. |
 |
Fig. (5) Consistency degree for 27 rounds. |
The Shapley value of the index attributes are calculated by (15) and (8), which obtains Shapley1=0.2935, Shapley2=0.1862, Shapley3=0.1317, Shapley4=0.2132 and Shapley5=0.1754.
From the subjective weights given by experts, the weight of the quantities of the restored load is much greater than that of the other attributes. It can be viewed as a scheme that focuses on the outstanding decision-making index according to the setting principle of λ in Sun et al. [26J.H. Sun, J. Hu, and Z. Liu, "New determining principle for λ-fuzzy measure and its application", Computer Engineering and Applications, vol. 50, pp. 249-255, 2014.], in which the adopted λ is close to −1. Therefore, λ=-0.99 in this study. Finally, the calculated and ranked fuzzy measures of all subsets are shown in Table 7.
The comprehensive Choquet integral value of each scheme is 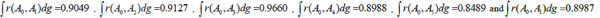 . The result of ranking is A3
. The result of ranking is A3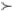 A2
A2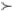 A1
A1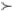 A4
A4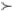 A6
A6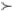 A5, from which A3 is the optimal solution, and A2 is suboptimal.
A5, from which A3 is the optimal solution, and A2 is suboptimal.
A comparison of the results in Zang et al. [5T.L. Zang, J.C. Zhong, Z.Y. He, and Q.Q. Qian, "Service restoration of distribution network based on heuristic rules and entropy weight", Power System Technology, vol. 36, pp. 251-257, 2012.] and Zang et al. [6T.L. Zang, Z.Y. He, D.Y. Ye, J.W. Yang, and Q.Q. Qian, "Distribution network service restoration based on interval number grey relation decision-making considering load change", Power System Protection and Control, vol. 41, pp. 38-43, 2013.] is shown in Table 8. From the comparison, the preferred scheme that this paper obtains is consistent with the results. AHP is used to calculate the subjective weights. However, in the example above, there is little qualitative data, so there will be too many subjective components if AHP is selected. The rankings of two from Zang et al. [5T.L. Zang, J.C. Zhong, Z.Y. He, and Q.Q. Qian, "Service restoration of distribution network based on heuristic rules and entropy weight", Power System Technology, vol. 36, pp. 251-257, 2012.] and Zang et al. [6T.L. Zang, Z.Y. He, D.Y. Ye, J.W. Yang, and Q.Q. Qian, "Distribution network service restoration based on interval number grey relation decision-making considering load change", Power System Protection and Control, vol. 41, pp. 38-43, 2013.] are different from each other, and there is an even a greater difference generated on the selection of A2. The entropy method and the grey correlation are both based on Euclidean distance, so they cannot eliminate the overlapping information, For example, the correlation coefficient between the quantities of the restored load and transferred load is −0.8572. The value under the quantities of the restored load is 0 and under the transferred load is 1 in scheme A2; such a value is just in line with the negative correlation between the two indices. From the examples above, the method of decision making proposed in this paper is superior and consistent with real conditions, compared to the previous method.
CONCLUSION
By using heuristic rules, several feasible service restoration schemes in a distribution network can be generated. This approach proposes a method of decision making that combines interval fuzzy preference relations, the Mahalanobis-Taguchi system, function and Choquet integral. The Shapley value contains subjective weights and overall importance of index attributes, by the expert group. This method constructs the decision-making model for the expert group by taking advantage of interval fuzzy preference relations to let the decision-making advice meet the requirement of consistency, and then obtains subjective weights. Then, the optimization model of the overall importance is constructed by the Mahalanobis-Taguchi system and the overall importance of each index attribute is obtained. The Shapley value is obtained using linear weighting, the fuzzy measure is identified, the comprehensive Choquet integral value of each restoration scheme is calculated, and the optimal restoration scheme is selected. This method not only avoids personal preferences in subjective decision making, but also eliminates overlapping information between attributes. It provides a new train of thought to the research on decision making for service restoration in a distribution network.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
The authors would like to acknowledge the support by National Natural Science Foundation of China (No. 71271084, 71671065). The Fundamental Research Funds for Central Universities (2016XS74) and the technology project of state grid (KJGW2015-020).
REFERENCES
| [1] | L. Liu, X.F. Chen, and D.H. Zhai, "Status and prospect of service restoration in smart distribution network", Power System Protection and Control, vol. 39, pp. 149-154, 2011. |
| [2] | S.P. Singh, G.S. Raju, and G.K. Rao, "A heuristic method for feeder reconfiguration and service restoration in distribution network", International Journal of Electrical Power and Energy Systems, vol. 31, pp. 309-314, 2009. [http://dx.doi.org/10.1016/j.ijepes.2009.03.013] |
| [3] | H.B. Zhang, X.Y. Zhang, and W.W. Tao, "A breadth-first search based service restoration algorithm for distribution network", Power System Technology, vol. 34, pp. 103-108, 2010. |
| [4] | Y.Y. Zhou, Q. Zhou, Y.M. Liu, Z.S. Yang, C.X. Sun, and Y. Dai, "Heuristic research and fuzzy evaluation for-post-fault restoration in distribution network", Journal of Chongqing University, vol. 33, pp. 78-82, 2010. |
| [5] | T.L. Zang, J.C. Zhong, Z.Y. He, and Q.Q. Qian, "Service restoration of distribution network based on heuristic rules and entropy weight", Power System Technology, vol. 36, pp. 251-257, 2012. |
| [6] | T.L. Zang, Z.Y. He, D.Y. Ye, J.W. Yang, and Q.Q. Qian, "Distribution network service restoration based on interval number grey relation decision-making considering load change", Power System Protection and Control, vol. 41, pp. 38-43, 2013. |
| [7] | D.Y. Shi, G.J. Xiong, J.F. Chen, and Y.H. Li, "Divisional fault diagnosis of power grids based on RBF neural network and choquet integral fusion", Proceedings of the CSEE, vol. 34, pp. 562-569, 2014. |
| [8] | J.C. Lu, H.L. Han, T.B. Liu, and Z.W. Zhao, "Comprehensive evaluation of power customer satisfaction degree based on choquet integral", Power System Technology, vol. 32, pp. 67-70, 2008. |
| [9] | M. Grabisch, I. Kojadinovic, and P. Meyer, "A review of methods for capacity identification in Choquet integral based multi-attribute utility theory", European Journal of Operational Research, vol. 186, pp. 766-785, 2008. [http://dx.doi.org/10.1016/j.ejor.2007.02.025] |
| [10] | M. Grabisch, and C. Labreuche, "A decade of application of the Choquet and Sugeno integrals in multi-criteria decision aid", A Quarterly Journal of Operations Research, vol. 6, pp. 1-44, 2008. [http://dx.doi.org/10.1007/s10288-007-0064-2] |
| [11] | J.Z. Wu, S.L. Yang, Q. Zhang, and S. Ding, "2-additive Capacity Identification Methods from Multicriteria Correlation Preference Information", IEEE Transactions on Fuzzy Systems, vol. 23, pp. 2094-2106, 2015. [http://dx.doi.org/10.1109/TFUZZ.2015.2403851] |
| [12] | Z.P. Chang, and L.S. Cheng, "Multi-attribute decision making method based on Mahalanobis-Taguchi System and Fuzzy Integral", Journal of Industrial Engineering, vol. 29, no. 3, pp. 107-115, 2015. |
| [13] | Z.P. Chang, and L.S. Cheng, "Choquet integral multi-attribute decision making method based on Mahalanobis-Taguchi system and φs transformation", Systems Engineering and Electronics, vol. 35, pp. 1702-1710, 2013. |
| [14] | Z.P. Chang, and L.S. Cheng, "Grey fuzzy integral correlation degree decision model based on Mahalanobis-Taguchi Gram-Schmidt and φs transformation", Control and Decision, vol. 29, pp. 1257-1261, 2014. |
| [15] | E. Takahagi, "On identification methods of fuzzy measures using weights and λ", Japanese Journal of Fuzzy Sets and System, vol. 12, pp. 665-676, 2000. |
| [16] | M. Sugeno, “Fuzzy Measure and Fuzzy Integrals, A Survey”, Fuzzy Automata and Decision Processes., North-Holland: New York, 1997. |
| [17] | Y. Tukamoto, "A measure theoretic approach to evaluation of fuzzy set defined on probability space", Journal of Fuzzy Mathematics, vol. 2, no. 3, pp. 89-98, 1982. |
| [18] | M. Grabisch, "The representation of importance and interaction of features by fuzzy measures", Pattern Recognition, vol. 17, no. 6, pp. 567-575, 1996. [http://dx.doi.org/10.1016/0167-8655(96)00020-7] |
| [19] | S.M. Chen, S.H. Cheng, and T.E. Lin, "Group decision making systems using group recommendations based on interval fuzzy preference relations and consistency matrices", Information Sciences, vol. 298, pp. 555-567, 2015. [http://dx.doi.org/10.1016/j.ins.2014.11.027] |
| [20] | T. Tanino, "Fuzzy preference orderings in group decision making", Fuzzy Sets and Systems, vol. 12, no. 2, pp. 117-131, 1984. [http://dx.doi.org/10.1016/0165-0114(84)90032-0] |
| [21] | E.H. Viedma, S. Alonso, F. Chiclana, and F. Herrera, "A consensus model for group decision making with incomplete fuzzy preference relations", IEEE Transactions on Fuzzy Systems, vol. 15, pp. 863-877, 2007. [http://dx.doi.org/10.1109/TFUZZ.2006.889952] |
| [22] | L.W. Lee, "Group decision making with incomplete fuzzy preference relations based on the additive consistency and the order consistency", Expert Systems with Applications, vol. 39, pp. 11666-11676, 2012. [http://dx.doi.org/10.1016/j.eswa.2012.04.043] |
| [23] | S.M. Chen, T.E. Lin, and L.W. Lee, "Group decision making using incomplete fuzzy preference relations based on the additive consistency and the order consistency", Information Sciences, vol. 259, pp. 1-15, 2014. [http://dx.doi.org/10.1016/j.ins.2013.08.042] |
| [24] | Z. Xu, "Consistency of interval fuzzy preference relations in group decision making", Applied Soft Computing, vol. 11, no. 5, pp. 3898-3909, 2011. [http://dx.doi.org/10.1016/j.asoc.2011.01.019] |
| [25] | G.L. Xu, and F. Liu, "An approach to group decision making based on interval multiplicative and fuzzy preference relations by using projection", Applied Mathematical Modelling, vol. 37, no. 6, pp. 3929-3943, 2013. [http://dx.doi.org/10.1016/j.apm.2012.08.007] |
| [26] | J.H. Sun, J. Hu, and Z. Liu, "New determining principle for λ-fuzzy measure and its application", Computer Engineering and Applications, vol. 50, pp. 249-255, 2014. |