- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Cybernetics & Systemics Journal
(Discontinued)
ISSN: 1874-110X ― Volume 12, 2018
Global Search PSO to Analyze the Values of Cultural and Creative Industries
Shen-Tsu Wang*, 1, Meng-Hua Li2
Abstract
Background:
Cultural and creative commodities and services are not evaluated by the service provider, but by the users. According to the preliminary interviews, it is incorrect to assume that the more expensive, the more consumers like the products.
Objective:
To analyze such commodities and services, this study employs a multi-objective planning model based on Value-Price-Cost theory to establish the relevant objectives and constraints.
Method:
A global search Particle Swarm Optimization (PSO) model is then established based on cluster analysis and grey theory. The three main operational mechanisms are: (1) an external repository to retain the optimal non-dominated solution set; (2) combined cluster analysis and grey theory to ensure a better distribution of the non-dominated solution search process; and (3) a virtual circle center, coupled with the existing positions of non-dominated solutions, to drive each particle of a multi-objective PSO (MOPSO) toward the optimal non-dominated solution.
Results:
The results of this research indicate that the proposed multi-objective algorithm outperforms both the conventional MOPSO and a non-dominated sorting genetic algorithm.
Conclusion:
The managerial implication is that high commodity prices increase the total project cost and extend the completion time, but reduce the customer’s quality evaluation of the commodity.
Article Information
Identifiers and Pagination:
Year: 2017Volume: 11
First Page: 67
Last Page: 84
Publisher Id: TOCSJ-11-67
DOI: 10.2174/1874110X01711010067
Article History:
Received Date: 29/06/2016Revision Received Date: 26/01/2017
Acceptance Date: 27/01/2017
Electronic publication date: 31/03/2017
Collection year: 2017
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
* Address correspondence to this author at the Department of Commerce Automation and Management, National Pingtung University, Taiwan, R.O.C., 51 Min Sheng E. Road, Pingtung, 900, Taiwan, R.O.C., Tel: 886-8-7663800, Fax: 886-8-7210801, E-mail: d917812@oz.nthu.edu.tw
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 29-06-2016 |
Original Manuscript | Global Search PSO to Analyze the Values of Cultural and Creative Industries | |
1. INTRODUCTION
The evaluation of cultural and creative commodities and services is user-oriented. In other words, the value is not determined by the service provider, but by the user after experiencing the commodities and services [1P. Holimchayachotikul, R. Derrouiche, D. Damand, and K. Leksakul, "Value creation through collaborative supply chain: holistic performance enhancement road map", Prod. Plann. Contr., vol. 25, pp. 912-922, 2014.
[http://dx.doi.org/10.1080/09537287.2013.780313] , 2U. Schultze, E. Prandelli, P.I. Salonen, and M.V. Alstyne, "Internet-enabled co-production: partnering or competing with customers?", Commun. AIS, vol. 19, pp. 294-324, 2007.]. There may be a considerable gap between the ‘service end’ and ‘customer end’ regarding perceptions about the commodity and service value. Therefore, in evaluating cultural and creative commodities and services, we must consider the optimization of multiple objectives, such as the firm’s profits and customer quality value. In the Value-Price-Cost (VPC) theoretical framework, V is the commodity quality as evaluated by the customer, P is the commodity price, and C is the total project cost to the firm [3E.V. Hippel, "Lead users: a source of novel product concepts", Manage. Sci., vol. 32, pp. 791-805, 2003.
[http://dx.doi.org/10.1287/mnsc.32.7.791] -5J. Zhang, G.J. Tang, and Y.Z. Luo, "Hybrid multi-objective optimisation for concurrent activities consolidating two docked spacecraft", Int. J. Syst. Sci., vol. 46, pp. 2905-2917, 2015.
[http://dx.doi.org/10.1080/00207721.2014.880198] ]. This study establishes multiple objectives and constraints based on the VPC theoretical framework for a multi-objective optimization model [6M.P. Biswal, and S. Acharya, "Multi-choice multi-objective mathematical programming model for integrated production planning: a case study", Int. J. Syst. Sci., vol. 44, pp. 1651-1665, 2013.
[http://dx.doi.org/10.1080/00207721.2012.669862] , 7A. Žilinskas, "A statistical model-based algorithm for ‘black-box’ multi-objective optimization", Int. J. Syst. Sci., vol. 45, pp. 82-93, 2014.
[http://dx.doi.org/10.1080/00207721.2012.702244] ]. In consideration of several objectives, this study aims to seek the most suitable solutions for customers and make the best schemes for suppliers.
Deng [8J.L. Deng, "Control problems of grey systems", Syst. Control Lett., vol. 1, pp. 288-294, 1982.
[http://dx.doi.org/10.1016/S0167-6911(82)80025-X] ] used a displacement operator and developed a transfer mechanism for the grey system. Kowalczyk [9R. Kowalczyk, "Using constraint satisfaction in genetic algorithms", Proc. Australian New Zealand Conf. Intell. Inf. Syst., 1996pp. 272-275 ] used dynamic project checking and constraint propagation during the main genetic algorithm (GA) simulation, whereas Barnier and Brisset [10N. Barnier, and P. Brisset, "Optimization by hybridization of a genetic algorithm and constraint satisfaction techniques", In: Proc. IEEE World Congr. Comput. Intell. Evol. Comput., 1998, pp. 645-649.
[http://dx.doi.org/10.1109/ICEC.1998.700115] ] considered sub-domains of the constraint satisfaction problem (CSP) within the GA. Deb et al. [11K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, "A fast and elitist multi-objective genetic algorithm: NSGA-II", IEEE Trans. Evol. Comput., vol. 6, pp. 182-197, 2002.
[http://dx.doi.org/10.1109/4235.996017] ] revised the definition of dominance to solve constrained multi-objective problems efficiently, and Coelle et al. [12C.A. Coello, G.T. Pulido, and M.S. Lechuga, "Handling multiple objectives with particle swarm optimization", IEEE Trans. Evol. Comput., vol. 8, pp. 256-279, 2004.
[http://dx.doi.org/10.1109/TEVC.2004.826067] ] used a number of test functions and metrics taken from the different evolutionary multi-objective optimization approaches. Zhang and Chau [13S. Zhang, and K.W. Chau, Dimension Reduction Using Semi-Supervised Locally Linear Embedding for Plant Leaf Classification: ICIC'09 Proceedings of the 5th International Conference, Emerging Intelligent Computing Technology and Applications, September 16-19, 2009, Ulsan, South Korea, Springer: New York, 2009, pp. 948-955.] adopted the K-Nearest Neighbor (K-NN) classifier, which features rapid training speed and simple structure. The features of plant leaves can be extracted and processed through semi-supervised locally linear embedding (SLLE) to form the input vector of K-NN. The results of the experiment by Wu et al. [14C.L. Wu, K.W. Chau, and Y.S. Li, "Methods to improve neural network performance in daily flows prediction", J. Hydro., vol. 372, pp. 80-93, 2009.
[http://dx.doi.org/10.1016/j.jhydrol.2009.03.038] ] demonstrated that the results of the original artificial neural network (ANN) are disappointing, as the predicted lagging effect is detected as 506. The technology developed by this study for pre-processing the three data can enhance the ANN performance. Chau and Wu [15K.W. Chau, and C.L. Wu, "A hybrid model coupled with singular spectrum analysis for daily rainfall prediction", J. Hydroinform., vol. 12, pp. 458-473, 2010.
[http://dx.doi.org/10.2166/hydro.2010.032] ] aimed to investigate the hybrid artificial neural networks (ANN)- support vector regression (SVR) of the combined effect, and determined how a singular spectrum can enhance the accuracy of predicting daily precipitation. The two daily precipitation records are taken as the test cases of different locations in China. The regular ANN is adopted as the benchmark. According to the study by Wang et al. [16W.C. Wang, K.W. Chau, D.M. Xu, and X.Y. Chen, "Improving forecasting accuracy of annual runoff time series using ARIMA based on EEMD decomposition", Water Resour. Manage., vol. 29, pp. 2655-2675, 2015.
[http://dx.doi.org/10.1007/s11269-015-0962-6] ], ensemble empirical mode decomposition (EEMD) can effectively increase the precision of forecasting; the proposed EEMD- auto regressive integrated moving average (ARIMA) model can significantly improve the ARIMA time sequence method of the annual runoff time sequence forecasting. Zeng et al. [17N. Zeng, Z. Wang, Y. Li, M. Du, and X. Liu, "Identification of nonlinear lateral flow immunoassay state space models via particle filter approach", IEEE Trans. NanoTechnol., vol. 11, pp. 321-327, 2012.
[http://dx.doi.org/10.1109/TNANO.2011.2171193] ] proposed the particle wave filtering algorithm, which integrated the core smooth method model with the horizontally-flowing immune testing state space model to measure short-term series. The Kalman filter was extended and selected as the important density particle wave filter, and the Metropolis-Hastings algorithm was adopted after the re-sampling to maintain the diversity of particles.
Lin and Hsieh [18C.J. Lin, and M.H. Hsieh, "Classification of mental task from EEG data using neural networks based on particle swarm optimization", Neurocomputing, vol. 72, pp. 1121-1130, 2009.
[http://dx.doi.org/10.1016/j.neucom.2008.02.017] ] used a neural classifier based on innovation particle swarm optimization (IPSO) to classify an electroencephalogram corresponding to left-hand movement. Goh et al. [19C.K. Goh, K.C. Tan, D.S. Liu, and S.C. Chiam, "A competitive and cooperative co-evolutionary approach to multi-objective particle swarm optimization algorithm design", Eur. J. Oper. Res., vol. 202, pp. 42-54, 2010.
[http://dx.doi.org/10.1016/j.ejor.2009.05.005] ] proposed a cooperative co-evolutionary multi-objective particle swarm optimization algorithm, and validated its performance through comparisons with existing multi-objective algorithms using established benchmarks and innovations. Tsai et al. [20S.J. Tsai, T.Y. Sun, C.C. Liu, S.T. Hsieh, W.C. Wu, and S.Y. Chiu, "An improved multi-objective particle swarm optimizer for multi-objective problems", Expert Syst. Appl., vol. 37, pp. 5872-5886, 2010.
[http://dx.doi.org/10.1016/j.eswa.2010.02.018] ] used a version of multi-objective PSO (MOPSO) to maintain the diversity of new non-dominated solutions via proportional distribution. Wang and Yang [21Y. Wang, and Y. Yang, "Particle swarm with equilibrium strategy of selection for multi-objective optimization", Eur. J. Oper. Res., vol. 200, pp. 187-197, 2010.
[http://dx.doi.org/10.1016/j.ejor.2008.12.026] ] used a method that increases the selective pressure, especially when the number of objectives is very large and complex. Alcayde et al. [22A. Alcayde, R. Baños, C. Gil, F.G. Montoya, J. Moreno-Garcia, and J. Gómez, "Annealing-tabu PAES: a multi-objective hybrid meta-heuristic", Optimization, vol. 60, pp. 1473-1491, 2011.
[http://dx.doi.org/10.1080/02331934.2010.505960] ] considered the different goal of Pareto-based multi-objective strategies to generate a front (set) of non-dominated solutions as an approximation to the true Pareto-optimal front solution. Sun et al. [23T.Y. Sun, C.C. Liu, S.J. Tsai, S.T. Hsieh, and K.Y. Li, "Cluster guide particle swarm optimization (CGPSO) for underdetermined blind source separation with advanced conditions", IEEE Trans. Evol. Comput., vol. 15, pp. 798-811, 2011.
[http://dx.doi.org/10.1109/TEVC.2010.2049361] ] proposed an algorithm in which a short-time Fourier transform is used to find a time-varying mixing matrix. Yao [24J.M. Yao, "Supply chain scheduling optimisation in mass customisation based on dynamic profit preference and application case study", Prod. Plann. Contr., vol. 22, pp. 690-707, 2011.
[http://dx.doi.org/10.1080/09537287.2010.537577] ] used supply chain scheduling optimization in mass customization based on dynamic profit and cost to solve these constraints. Fuchs [25B. Fuchs, "Transforming lead user innovations into new corporate ventures: a matter of information asymmetry?", Int. J. Entrep. Innov. Manag., vol. 14, pp. 80-95, 2011.
[http://dx.doi.org/10.1504/IJEIM.2011.040823] ] found that information asymmetries exist because of interdisciplinary project teams, latency of needs, and the advance prototyping efforts of lead users. The method of Villalobos-Arias et al. [26M.A. Villalobos-Arias, G.T. Pulido, and C.A. Coello, "A new mechanism to maintain diversity in multi-objective metaheuristics", Optimization, vol. 61, pp. 823-854, 2012.
[http://dx.doi.org/10.1080/02331934.2010.534476] ] applies stripes in the objective function space, and is independent of the search solution. Jolai et al. [27F. Jolai, R. Tavakkoli-Moghaddam, and M. Taghipour, "A multi-objective particle swarm optimisation algorithm for unequal sized dynamic facility layout problem with pickup/drop-off locations", Int. J. Prod. Res., vol. 50, pp. 4279-4293, 2012.
[http://dx.doi.org/10.1080/00207543.2011.613863] ] used a MOPSO algorithm to find near-optimal solutions. Zhang and Chau [28J. Zhang, and K.W. Chau, "Multilayer ensemble pruning via novel multi-sub-swarm particle swarm optimization", J. Univ. Compt. Sci., vol. 15, pp. 840-858, 2009.] argued that a larger number of layers would enhance the performance of the layers; however, according to the experimental results, the performance of trimming depends on various basic classifiers, and the proposed model is not immune to this problem. Taormina and Chau [29R. Taormina, and K.W. Chau, "Data-driven input variable selection for rainfall–runoff modeling using binary-coded particle swarm optimization and extreme learning machines", J. Hydroinform., vol. 529, pp. 1617-1632, 2015.] explored the application of fast and accurate wrapper Input Variable Selection (IVS) for Extreme Learning Machines (ELM) to develop rainfall runoff data-drive modeling and binary-coded discrete group optimization, and concluded that returned Pareto-fronts allowed the selected input that defined relative importance, which cannot usually be achieved with other wrapper methods, such as the Binary-coded discrete Fully Informed Particle Swarm optimization (BFIPS)-ELM method.
Cabrerizo et al. [30F.J. Cabrerizo, E. Herrera-Viedma, and W. Pedrycz, "A method based on PSO and granular computing of linguistic information to solve group decision making problems defined in heterogeneous contexts", Eur. J. Oper. Res., vol. 230, pp. 624-633, 2013.
[http://dx.doi.org/10.1016/j.ejor.2013.04.046] ] presented an innovative granulation of the linguistic information used in group decision making methods defined in heterogeneous contexts. Dang et al. [31D.C. Dang, R.N. Guibadj, and A. Moukrim, "An effective PSO-inspired algorithm for the team orienteering problem", Eur. J. Oper. Res., vol. 229, pp. 332-344, 2013.
[http://dx.doi.org/10.1016/j.ejor.2013.02.049] ] proposed an efficient evaluation process for the Team Orienteering Problem (TOP) based on an interval graph model and a PSO inspired algorithm. Ozsoydan and Sipahioglu [32F.B. Ozsoydan, and A. Sipahioglu, "Heuristic solution approaches for the cumulative capacitated vehicle routing problem", Optimization, vol. 62, pp. 1321-1340, 2013.
[http://dx.doi.org/10.1080/02331934.2013.841158] ] focused on comparing the performance of neighborhood- and population-based methods for the problem of cumulative capacitated vehicle routing, while Kou et al. [33J. Kou, S. Xiong, Z. Fang, X. Zong, and Z. Chen, "Multiobjective optimization of evacuation routes in stadium using superposed potential field network based ACO", Comput. Intell. Neurosci., vol. 2013, no. 369016, p. 369016, 2013.
[PMID: 23861678] ] used the evacuation zone as a superposed potential field network, and presented an ant colony optimization algorithm to solve related problems. Validi et al. [34S. Validi, A. Bhattacharya, and P.J. Byrne, "Integrated low-carbon distribution system for the demand side of a product distribution supply chain: A DoE-guided MOPSO optimiser-based solution approach", Int. J. Prod. Res., vol. 52, pp. 3074-3096, 2014.
[http://dx.doi.org/10.1080/00207543.2013.864054] ] employed the MOPSO optimizer to eliminate unrealistic solutions, using a popular multi-attribute decision-making approach to evaluate the solutions within the Pareto optimal solution space. Hung and Maleki [4K.T. Hung, and H. Maleki, "Applying group technology to the forging industry", Prod. Plann. Contr., vol. 25, pp. 134-148, 2014.
[http://dx.doi.org/10.1080/09537287.2013.782948] ] applied group technology to the forging operations of the Tabriz Tractor Manufacturing Industry, and Holimchayachotiku et al. [1P. Holimchayachotikul, R. Derrouiche, D. Damand, and K. Leksakul, "Value creation through collaborative supply chain: holistic performance enhancement road map", Prod. Plann. Contr., vol. 25, pp. 912-922, 2014.
[http://dx.doi.org/10.1080/09537287.2013.780313] ] introduced the innovative idea of measuring value added along the supply chain using a collaborative method. Jamian et al. [35J.J. Jamian, M.N. Abdullah, H. Mokhlis, M.W. Mustafa, and A.H. Bakar, "Global particle swarm optimization for high dimension numerical functions analysis", J. Appl. Math., vol. 2014, pp. 1-14, 2014.
[http://dx.doi.org/10.1155/2014/329193] ] solved a series of complex problems using global PSO, and Jakubcová et al. [36M. Jakubcová, P. Máca, and P. Pech, "A comparison of selected modifications of the particle swarm optimization algorithm", J. Appl. Math., vol. 2014, pp. 1-10, 2014.
[http://dx.doi.org/10.1155/2014/293087] ] found a better modification of the PSO algorithm using adaptive inertia weights. Perez-Cisneros et al. [37V. Osuna-Enciso, E. Cuevas, D. Oliva, V. Zúñiga, M. Pérez-Cisneros, and D. Zaldívar, "A multi-objective approach to homography estimation", Comput. Intell. Neurosci., vol. 2016, p. 3629174, 2016.
[http://dx.doi.org/10.1155/2016/3629174] [PMID: 26839532] ] considered an estimation method for multi-objective programming, with many matching points and multiple solutions being simultaneously optimized. Zeng et al. [38N. Zeng, Z. Wang, Y. Li, M. Du, and X. Liu, "A hybrid EKF and switching PSO algorithm for joint state and parameter estimation of lateral flow immunoassay models", IEEE/ACM Trans. Comput. Biol. Bioinformatics, vol. 9, no. 2, pp. 321-329, 2012.
[http://dx.doi.org/10.1109/TCBB.2011.140] [PMID: 22025755] ] proposed the hybrid extended Kalman filter (EKF) to combine the PSO algorithms of an inequality constraint for a system state. With maximum probability, the constraint of the state variable in the dynamic state estimate can solve the problem of constraint optimization through the combined EKF algorithm. Zeng et al. [39N. Zeng, Y.S. Hung, Y. Li, and M. Du, "A novel switching local evolutionary PSO for quantitative analysis of lateral flow immunoassay", Expert Syst. Appl., vol. 41, pp. 1708-1715, 2014.
[http://dx.doi.org/10.1016/j.eswa.2013.08.069] ] proposed the new PSO for quantitative analysis of the lateral flow immunoassay (LFIA) of the non-homogeneous Markov chain and differential evolution (DE). Zeng et al. [40N. Zeng, Z. Wang, H. Zhang, and F.E. Alsaadi, "A novel switching delayed PSO algorithm for estimating unknown parameters of lateral flow immunoassay", Cognit. Comput., vol. 8, pp. 143-152, 2016.
[http://dx.doi.org/10.1007/s12559-016-9396-6] ] demonstrated that the new switching delayed particle swarm optimization (SDPSO) was better than some famous PSO algorithms in terms of overall search and convergence efficiency. Zeng et al. [41N. Zeng, H. Zhang, Y. Chen, B. Chen, and Y. Liu, "Path planning for intelligent robot based on switching local evolutionary PSO algorithm", Assem. Autom., vol. 36, pp. 120-126, 2016.
[http://dx.doi.org/10.1108/AA-10-2015-079] ] confirmed that the switching local evolutionary PSO (SLEPSO) could be applied to the path planning in two different environments.
Cultural and creative commodities and services are not evaluated by the service provider, but by the users. According to the preliminary interviews, it is incorrect to assume that the more expensive, the more consumers like the products. To analyze such commodities and services, this study employs a multi-objective planning model based on Value-Price-Cost theory to establish the relevant objectives and constraints. This study integrates the global search PSO algorithm based on cluster analysis, the CSP of grey theory, the non-dominated sorting genetic algorithm II (NSGAII), and a particle filtering algorithm. The integrated algorithm gives the non-overlapped distribution of the non-dominated solutions. Whether the problem is convex or non-convex, our method can determine the Pareto front. The proposed algorithm considers the dispersion, scalability, and improved precision of non-dominated solutions. This enables the particles to reach the optimal solution faster in the evolutionary process, thus avoiding the stagnation caused by complex problems or increased dimensionality. The particle filtering algorithm is used to replace the conditions meeting the constraints, resulting in unsatisfactory rules. With the PSO computing technique and optimal solution search capability, the search space can be reduced, and the search can be accelerated [42W. Li, C. Zhao, and D. Li, "Flowshop with multiple processors dynamic scheduling problem based on hybrid genetic-particle swarm optimization", Open Cybernet. Sys. J., vol. 9, pp. 1038-1044, 2015.-44N. Tao, G. Chen, R. Chen, and H. Jin, "A novel hybrid method for solving flexible job-shop scheduling problem", Open Cybernet. Sys. J., vol. 10, pp. 13-19, 2016.].
2. MULTI-OBJECTIVE MODEL ESTABLISHMENT AND ALGORITHM
2.1. Multi-objective Mathematical Model Establishment
The mathematical symbols used throughout the remainder of this paper are defined as follows [6M.P. Biswal, and S. Acharya, "Multi-choice multi-objective mathematical programming model for integrated production planning: a case study", Int. J. Syst. Sci., vol. 44, pp. 1651-1665, 2013.
[http://dx.doi.org/10.1080/00207721.2012.669862] , 20S.J. Tsai, T.Y. Sun, C.C. Liu, S.T. Hsieh, W.C. Wu, and S.Y. Chiu, "An improved multi-objective particle swarm optimizer for multi-objective problems", Expert Syst. Appl., vol. 37, pp. 5872-5886, 2010.
[http://dx.doi.org/10.1016/j.eswa.2010.02.018] ]:
J: Firm code or subscript set.
i:: Any firm code or subscript, where i
 j.
j.
S: Commodity variety code or subscript set.
j: Any commodity variety code or subscript, where j
 S.
S.
Oj Code of all commodities in commodity category j or subscript set, where j
 S.
S.
k: Any commodity code or subscript, where k
 O, j
O, j
 S.
S.
Ci The upper limit of capital that can be used by firm i, where i
 J.
J.
Tij The expected total demand of all commodities in commodity category j of firm i in the next phase in related markets, where i
 J, j
J, j
 S.
S.
Sijk: The quality evaluation of general customers regarding commodity k in commodity category j from firm i in the long term, where i
 J, j
J, j
 S, k
S, k
 Oj.
Oj.
fij: The upper limit of the number of commodities in commodity category j, according to the decision maker of firm i, where i
 J, j
J, j
 S,.
S,.
ujk: The unit volume of commodity k in commodity category j, where j
 S, k
S, k
 Oj.
Oj.
tiFirm i upper bound of inventory volume, where i
 J.
J.
Yi(rijk, hi) The expected demand for commodity k in commodity category j of firm i, under the conditions of economic cyclical factor hi and commodity price rijk, where i
 J, j
J, j
 S, k
S, k
 Oj; the same commodity may be sold at different prices at different locations.
Oj; the same commodity may be sold at different prices at different locations.
The following economic monitoring signals, as defined by the Division of Economic Research, Economic Construction Commission, Executive Yuan, are also used.
Red (R): overheated economy, the government should adopt austerity measures to gradually resume normal economic conditions.
Yellow-red (YR): the economy is active, which is an indicative signal. The government should closely watch follow-up economic trends, and take timely responsive measures.
Green light (G): economic prosperity and stability.
Yellow-blue (YB): the economy is poor, which is an indicative signal. The government should closely watch follow-up economic trends, and take timely responsive measures.
Blue light (B): economic recession, the government should make strong efforts to stimulate economic recovery policies.
M: A large positive number,M 0.
(a,b): Job between events a and b.
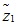 : Total project cost.
: Total project cost.
z2: Total completion time.
Dab: Job normal job time.
dab: Job shortest job time.
CDab: Job normal (direct) job time.
Cdab: Job shortest (direct) job time.
mab: Job crashing cost slope.
tab: Job actual job time.
Gab: Job (a, b) crashing time.
Fa: Event a earliest start time.
Fb: Event b earliest start time.
F1: Project start time.
Fn: Project completion time.
Vo: Project completion time under normal conditions.
V: Agreed project completion time.
N1: Fixed indirect costs under normal conditions.
n: Unit indirect change cost.
E: Total budget.
Definitions of decision making variables:
qijk: The number of commodities k available to purchase in commodity category j, as planned by firm i, where i
 J, j
J, j
 S, k
S, k
 Oj.
Oj.
Wijk: The decision-making variables regarding the purchase of commodity k in commodity category j, as planned by firm i. If Wijk = 1, then the commodity is purchased. Otherwise, Wijk = 0, where i
 J,j
J,j
 S,k
S,k
 Oj..
Oj..
rijk: The current price of commodity k in commodity category j set by firm i, where i
 J,j
J,j
 S,k
S,k
 Oj..
Oj..
The target equations and constraints can be described as follows.
Target equation (1) represents the expected total profit of the current commodity purchasing and pricing decisions of firm
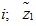 in target equations (1) and (4) is the minimization of the total project cost; the crashing cost slope (mab) and unit indirect cost (mab) are not precise and follow a triangular probability distribution. Target equation (2) gives the expected total market share of the current commodity purchasing and pricing decisions of firm i. Target equation (3) expresses the minimization of the total completion time and the minimized proportion of customer quality evaluations of firm i; z2 in target equations (3) and (5) represents the desired level of the fuzzy target function. Regarding practical project management decision-making problems, lack of information means that the total completion time often contains a considerable degree of uncertainty. As a result, the total completion time is a fuzzy target function with an imprecise value. The target value often varies according to the judgment of decision makers [45T.F. Liang, "Fuzzy multi-objective project management decisions using two-phase fuzzy goal programming approach", Comput. Ind. Eng., vol. 57, pp. 1407-1416, 2009.
in target equations (1) and (4) is the minimization of the total project cost; the crashing cost slope (mab) and unit indirect cost (mab) are not precise and follow a triangular probability distribution. Target equation (2) gives the expected total market share of the current commodity purchasing and pricing decisions of firm i. Target equation (3) expresses the minimization of the total completion time and the minimized proportion of customer quality evaluations of firm i; z2 in target equations (3) and (5) represents the desired level of the fuzzy target function. Regarding practical project management decision-making problems, lack of information means that the total completion time often contains a considerable degree of uncertainty. As a result, the total completion time is a fuzzy target function with an imprecise value. The target value often varies according to the judgment of decision makers [45T.F. Liang, "Fuzzy multi-objective project management decisions using two-phase fuzzy goal programming approach", Comput. Ind. Eng., vol. 57, pp. 1407-1416, 2009.
[http://dx.doi.org/10.1016/j.cie.2009.07.010] , 46T.F. Liang, and H.W. Cheng, "Multi-objective aggregate production planning decisions using two-phase fuzzy goal programming method", J. Ind. Manag. Optim., vol. 7, pp. 365-383, 2011.
[http://dx.doi.org/10.3934/jimo.2011.7.365] ].
Equations (6)–(12) represent the constraints of the relevant variables of firm i in terms of purchasing commodity k in category j. Equations (13)–(16) express the sequence of jobs, the tolerable crash time, and the actual job time. In general, these are equations of certainty. In practice, because of the dynamics of enterprise environments and industrial competition, as well as project contractual content and resource supply uncertainty, the agreed project completion time in equation (17) is often imprecise by nature. In equation (18), the fund raising, manipulation, and resource prices of the enterprise often result in an uncertain actual cost. Equation (19) expresses the non-negativity constraints of certain variables [45T.F. Liang, "Fuzzy multi-objective project management decisions using two-phase fuzzy goal programming approach", Comput. Ind. Eng., vol. 57, pp. 1407-1416, 2009.
[http://dx.doi.org/10.1016/j.cie.2009.07.010] , 46T.F. Liang, and H.W. Cheng, "Multi-objective aggregate production planning decisions using two-phase fuzzy goal programming method", J. Ind. Manag. Optim., vol. 7, pp. 365-383, 2011.
[http://dx.doi.org/10.3934/jimo.2011.7.365] ].
2.2. Algorithm Steps
The proposed algorithm proceeds as follows [8J.L. Deng, "Control problems of grey systems", Syst. Control Lett., vol. 1, pp. 288-294, 1982.
[http://dx.doi.org/10.1016/S0167-6911(82)80025-X] , 12C.A. Coello, G.T. Pulido, and M.S. Lechuga, "Handling multiple objectives with particle swarm optimization", IEEE Trans. Evol. Comput., vol. 8, pp. 256-279, 2004.
[http://dx.doi.org/10.1109/TEVC.2004.826067] , 14C.L. Wu, K.W. Chau, and Y.S. Li, "Methods to improve neural network performance in daily flows prediction", J. Hydro., vol. 372, pp. 80-93, 2009.
[http://dx.doi.org/10.1016/j.jhydrol.2009.03.038] , 16W.C. Wang, K.W. Chau, D.M. Xu, and X.Y. Chen, "Improving forecasting accuracy of annual runoff time series using ARIMA based on EEMD decomposition", Water Resour. Manage., vol. 29, pp. 2655-2675, 2015.
[http://dx.doi.org/10.1007/s11269-015-0962-6] , 18C.J. Lin, and M.H. Hsieh, "Classification of mental task from EEG data using neural networks based on particle swarm optimization", Neurocomputing, vol. 72, pp. 1121-1130, 2009.
[http://dx.doi.org/10.1016/j.neucom.2008.02.017] , 23T.Y. Sun, C.C. Liu, S.J. Tsai, S.T. Hsieh, and K.Y. Li, "Cluster guide particle swarm optimization (CGPSO) for underdetermined blind source separation with advanced conditions", IEEE Trans. Evol. Comput., vol. 15, pp. 798-811, 2011.
[http://dx.doi.org/10.1109/TEVC.2010.2049361] , 24J.M. Yao, "Supply chain scheduling optimisation in mass customisation based on dynamic profit preference and application case study", Prod. Plann. Contr., vol. 22, pp. 690-707, 2011.
[http://dx.doi.org/10.1080/09537287.2010.537577] ].
2.2.1. Using the Cluster Mechanism and Grey Theory to Obtain a More Dispersed Non-dominated Solution Set
In recent years, the optimization of multi-objective problems has focused on determining the distribution of the solution sets in the target space, rather than determining the Pareto front. Thus, appropriate solutions can be determined for multi-objective problems. This study uses the cluster mechanism, and expects that solutions in the repository can be dispersed in a non-overlapped Manner. Moreover, the differences between non-dominated solutions can be enhanced using the geometric features of the particle swarms in the target space. The cluster mechanism first selects a stored non-dominated solution as the first cluster center, and calculates the radius r of the circle. Other solutions within a distance r of the cluster center solution belong to the same cluster. The solution at the center of the circle is retained, and the other solutions in the cluster are removed under the assumption that they are very similar to the center solution. In this way, more diversified solutions are expected to be stored. As far as the image of information is concerned, the grey theory believes that the system presents the problematic or partial image elements. In respect of the scale of information, it points out that only an interval can be obtained, and that it is impossible to achieve accurate values in terms of the measurable scale of the system. These are also core problems to be addressed by the grey theory. In comparison with statistical methods, the grey theory is special in that the researcher cannot receive adequate information about the truth, but is still able to use the small quantity of information (small-sampled and abnormal) without a specific distribution in order to conduct the grey system theory analysis [8J.L. Deng, "Control problems of grey systems", Syst. Control Lett., vol. 1, pp. 288-294, 1982.
[http://dx.doi.org/10.1016/S0167-6911(82)80025-X] ].
Regarding the cluster radius r, we calculate the range of the non-dominated solution currently stored in the repository of n target functions, and obtain the minimal value of the n ranges. The minimal value is divided by n times the External Repository Size (ERS). The cluster radius r is expressed in Eq. (20). The cluster algorithm proceeds as follows:
- use the non-dominated solution currently stored in the repository to calculate the range of the target function, and use Eq. (20) to calculate the cluster radius r.
- the first solution in the repository is set as the center of the first cluster.
- the distance of the second solution from the current cluster center is computed. If it is less than the cluster radius r, the solution belongs to the same cluster; if it is greater than the cluster radius, the solution becomes the center of a new cluster.
- return to Step 3 until all solutions have been assigned to a cluster.
- for all clusters with more than one solution, remove redundant solutions using grey relational analysis to obtain the cluster center solution.
The degree of relationship among sub-systems or elements can be evaluated through grey relational analysis [8J.L. Deng, "Control problems of grey systems", Syst. Control Lett., vol. 1, pp. 288-294, 1982.
[http://dx.doi.org/10.1016/S0167-6911(82)80025-X] ], whereby the factors that influence the development trend are determined in order to learn the major features of the system. This process has the following steps. Grey relational analysis is supposed to calculate the measures among discrete series, but the data in the series must be consistent with the comparability of the series. Hence, it is necessary to pre-process the whole group of series in the form of statistical analysis. Such a process is called “grey relational generation”. The procedure is called normalization, and different factors can be taken into quantitative or qualitative (satisfaction) consideration [8J.L. Deng, "Control problems of grey systems", Syst. Control Lett., vol. 1, pp. 288-294, 1982.
[http://dx.doi.org/10.1016/S0167-6911(82)80025-X] ].
- Normalize the original data by dividing the xi (k) by the mean value of the sequence, as shown in Eq. (21).
- Designate the standard sequence and calculate the difference sequence. Take the mean value as a standard sequence, i.e. , sequence 0; the difference sequence Δ0i (k) indicates the absolute difference of elements k between sequence i and sequence 0, as expressed in Eq. (22).
- Calculate the maximal difference Δmax and minimal difference Δmin, as expressed in Eqs. (23) and (24).
- Calculate the grey relational coefficient γ0i(k). The relational coefficient γ0i(k) is defined in Eq. (25), x where is the adjustment factor.
The adjustment factor is ς, and ς [0,1]. In general, the value of the recognition coefficient is set as “0.5”, but it can be adjusted according to the actual needs to increase the difference in the result. When ς the is smaller, and the greater the correlation analysis is resolution [8J.L. Deng, "Control problems of grey systems", Syst. Control Lett., vol. 1, pp. 288-294, 1982.
[http://dx.doi.org/10.1016/S0167-6911(82)80025-X] ].
Step 5: Calculate the grey relationship Г0i between each sequence and the standard sequence. The grey relationship Г0i is defined in Eq. (26).
Step 6: Conduct sequencing according to the grey relationship.
Using a multi-objective problem with n targets as an example, Eq. (27) represents the coordinates of the circle center, where k represents the size of the external repository, w is the particle position, and Fn(.) is the nth target function.
After obtaining the circle center, we connect it to the non-dominated solutions in other repositories and the solutions determined by the particles. After the accumulation process described by Eq. (28), we obtain Eq. (29) to determine the angle between the two vectors.
where wj is the solution determined by particle j, wnk is the kth non-dominated solution in the external repository, and oFn is the assumed circle center according to Eq. (29).
After determining the angle between each particle and the non-dominated solutions in the repository, the particle selects the non-dominated solution with the smallest angle as the global optimal solution, and updates its velocity for the next iteration.
2.2.2. Constraint Satisfaction Problem (CSP)
The CSP comprises a group of variables and constraints, where each variable has a given range. The constraint describes the correlation between variables, and CSP aims to determine the solution to all related constraints.
The CSP is an NP-complete problem, and thus appropriate solutions are generally lacking. Some scholars have proposed different methods to solve CSP. Constraint propagation has been used to reduce the size of the search space, backtracking has been directly applied to search for the probable solution, and a combined tree-search and consistent algorithm has been developed to effectively determine one or multiple applicable solutions. Nadel [47B. Nadel, "Tree search and arc consistency in constraint satisfaction algorithms", In: L. Kanal, and V. Kumar, Eds., Search in Artificial Intelligence., Springer-Verlag: New York, 1998, pp. 287-342.] compared the effectiveness of several such algorithms. The major difference is the consistency of the nodes in the course of solving the tree structure. The main characteristic of hybrid techniques is that, when a new value is assigned to a variable, all related constraints are examined, and all values that fail to meet the constraints are filtered so that the probable solution values remain consistent. If the probable range of these variables becomes empty, there is contradiction between the constraints, and the backtracking algorithm must be used. Constraint satisfaction problem (CSP) is one type of complex problems, and so it is difficult to find an appropriate solution to it. Scholars have put forward a wide range of solutions. Constraint propagation has been adopted to narrow the search space, and recalling has been applied to the search for possible solutions. Moreover, the literature has developed the combined tree-search and consistent algorithm to define one or more applicable solutions [9R. Kowalczyk, "Using constraint satisfaction in genetic algorithms", Proc. Australian New Zealand Conf. Intell. Inf. Syst., 1996pp. 272-275 , 10N. Barnier, and P. Brisset, "Optimization by hybridization of a genetic algorithm and constraint satisfaction techniques", In: Proc. IEEE World Congr. Comput. Intell. Evol. Comput., 1998, pp. 645-649.
[http://dx.doi.org/10.1109/ICEC.1998.700115] ].
Barnier and Brisset [10N. Barnier, and P. Brisset, "Optimization by hybridization of a genetic algorithm and constraint satisfaction techniques", In: Proc. IEEE World Congr. Comput. Intell. Evol. Comput., 1998, pp. 645-649.
[http://dx.doi.org/10.1109/ICEC.1998.700115] ] proposed a hybrid system that integrates a GA with a constraint satisfaction technique. This method solves the CSP to reduce the search space, and improves the computing efficiency of the GA by constraint satisfaction-based inference. Kowalczyk [9R. Kowalczyk, "Using constraint satisfaction in genetic algorithms", Proc. Australian New Zealand Conf. Intell. Inf. Syst., 1996pp. 272-275 ] proposed using the concept of constraint satisfaction in a GA. However, few studies have used constraint inference to improve the computational efficiency of PSO. Thus, there is no systematic description of how to integrate problem constraints and user requirements into a constraint network.
2.2.3. System Construction
Some recent studies have combined the constraint inference mechanism with NSGAII. The experimental results showed that constraint inference was very effective at remedying the defects in NSGAII when solving complex problems. Therefore, we propose a hybrid method that combines PSO with NSGAII, and use particle filtering to accelerate the search. This overcomes the stagnation problem caused by complex problems or an increase in dimensionality. The particle filtering algorithm replaces the conditions meeting the constraints, but this produces an unsatisfactory rule. With the PSO computing technique and optimal solution search capability, the search space can be reduced, and the search can be accelerated. In traditional PSO updating, particles refer to the optimal solutions of individuals and groups, and weight is employed to update speed and then location. PSO and NSGAII use the adaptability function to evaluate the classification rules, and an increase in the problems’ complexity tends to lengthen the time of search, which can lead to partial optimization. Therefore, we proposed PSO and a hybrid and a new updating mechanism [10N. Barnier, and P. Brisset, "Optimization by hybridization of a genetic algorithm and constraint satisfaction techniques", In: Proc. IEEE World Congr. Comput. Intell. Evol. Comput., 1998, pp. 645-649.
[http://dx.doi.org/10.1109/ICEC.1998.700115] , 12C.A. Coello, G.T. Pulido, and M.S. Lechuga, "Handling multiple objectives with particle swarm optimization", IEEE Trans. Evol. Comput., vol. 8, pp. 256-279, 2004.
[http://dx.doi.org/10.1109/TEVC.2004.826067] , 18C.J. Lin, and M.H. Hsieh, "Classification of mental task from EEG data using neural networks based on particle swarm optimization", Neurocomputing, vol. 72, pp. 1121-1130, 2009.
[http://dx.doi.org/10.1016/j.neucom.2008.02.017] , 19C.K. Goh, K.C. Tan, D.S. Liu, and S.C. Chiam, "A competitive and cooperative co-evolutionary approach to multi-objective particle swarm optimization algorithm design", Eur. J. Oper. Res., vol. 202, pp. 42-54, 2010.
[http://dx.doi.org/10.1016/j.ejor.2009.05.005] ].
The architecture proposed in this paper is based on PSO and the particle filtering algorithm in the constraint-based PSO (CBPSO) module. To improve the effectiveness of the particle swarm, we propose two improved update mechanisms, one for PSO and one for NSGAII. Fig. (1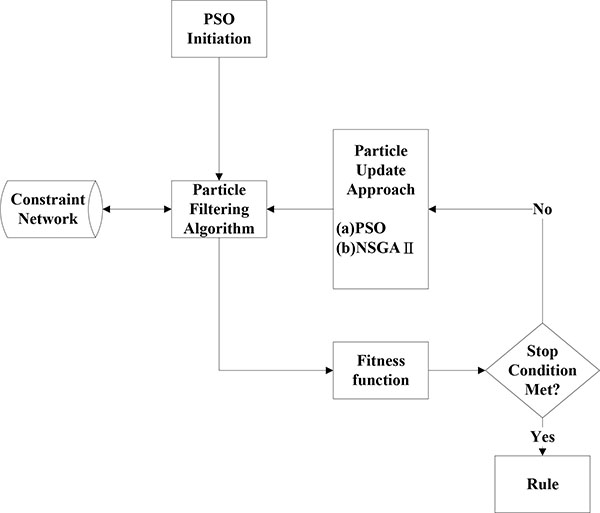 ) shows the research architecture. First, the PSO initiation module randomly generates particles according to the initial parameters. The particle filtering algorithm then filters the classification rule represented by each particle into reasonable and acceptable classification rules. The termination criterion is judged by calculating the fitness function. If the stop condition is not met, the velocity and position of each particle is updated, and the particle filtering algorithm checks the generated particles. In particle initiation and evolution, each particle must be filtered into a reasonable and acceptable form. When a particle is updated, its fitness is calculated, and Pid, Pgdare recorded. The set of local variables is then defined as fitness function, and the process is repeated until the constraints are met as shown in Fig. (1
) shows the research architecture. First, the PSO initiation module randomly generates particles according to the initial parameters. The particle filtering algorithm then filters the classification rule represented by each particle into reasonable and acceptable classification rules. The termination criterion is judged by calculating the fitness function. If the stop condition is not met, the velocity and position of each particle is updated, and the particle filtering algorithm checks the generated particles. In particle initiation and evolution, each particle must be filtered into a reasonable and acceptable form. When a particle is updated, its fitness is calculated, and Pid, Pgdare recorded. The set of local variables is then defined as fitness function, and the process is repeated until the constraints are met as shown in Fig. (1 ) [48M.J. Alves, and J.P. Costa, "An algorithm based on particle swarm optimization for multiobjective bilevel linear problems", Appl. Math. Comput., vol. 247, pp. 547-561, 2014.
) [48M.J. Alves, and J.P. Costa, "An algorithm based on particle swarm optimization for multiobjective bilevel linear problems", Appl. Math. Comput., vol. 247, pp. 547-561, 2014.
[http://dx.doi.org/10.1016/j.amc.2014.09.013] -52N. Srinivas, and K. Deb, "Multi-objective optimization using non-dominated sorting in genetic algorithms", Evol. Comput., vol. 2, pp. 221-248, 1994.
[http://dx.doi.org/10.1162/evco.1994.2.3.221] ]. Some recent studies have integrated the constraint inference mechanism with NSGAII, and according to their results, the constraint inference is very effective in solving the problems in NSGAII. Therefore, we proposed a hybrid method that combined PSO with NSGAII and adopted the Particle Filter Algorithm to facilitate the search. This solved the stagnation caused by complex problems or the increase in dimension. The Particle Filter Algorithm substituted the conditions that met the constraints, but this led to unsatisfactory rules. PSO and the ability to search for the optimal solution can reduce the search space and facilitate the search, thus allowing the effective integration and application of Particle Filter Algorithm in the solution of some problems [10N. Barnier, and P. Brisset, "Optimization by hybridization of a genetic algorithm and constraint satisfaction techniques", In: Proc. IEEE World Congr. Comput. Intell. Evol. Comput., 1998, pp. 645-649.
[http://dx.doi.org/10.1109/ICEC.1998.700115] , 12C.A. Coello, G.T. Pulido, and M.S. Lechuga, "Handling multiple objectives with particle swarm optimization", IEEE Trans. Evol. Comput., vol. 8, pp. 256-279, 2004.
[http://dx.doi.org/10.1109/TEVC.2004.826067] , 18C.J. Lin, and M.H. Hsieh, "Classification of mental task from EEG data using neural networks based on particle swarm optimization", Neurocomputing, vol. 72, pp. 1121-1130, 2009.
[http://dx.doi.org/10.1016/j.neucom.2008.02.017] , 19C.K. Goh, K.C. Tan, D.S. Liu, and S.C. Chiam, "A competitive and cooperative co-evolutionary approach to multi-objective particle swarm optimization algorithm design", Eur. J. Oper. Res., vol. 202, pp. 42-54, 2010.
[http://dx.doi.org/10.1016/j.ejor.2009.05.005] ].
In the particles, the set of local variables Up consists of two sets: one is the set with values (x1, = v1,...,xp = vp), and the other is the set without values (xp+1, ..., xm). Let U 0 be the set of variables with values, and Um be the set of all m variables with values.
In the architecture of CBPSO, each position value is limited during the particle construction stage. Thus, the initial swarm, as well as the swarms generated during the execution of the algorithm, is processed by constraint inference and the position selection mechanism. Basically, CBPSO uses particle filtering to execute constraint inference. The main technique is forward checking, whereby constraint information is used to determine acceptable position values, limit the effective range of the position values within the constraint network, and use related constraints to limit the range of the other positions.
In the particle filtering algorithm, the constraint set V must be satisfied within the constraint network (X, D, V). Up is the set of local position variables with values, meaning the local position has a value.
 |
Fig. (1) Hybrid PSO algorithm. |
The particle filtering algorithm appoints a set containing a single constraint F, and this set is determined by Up, from the set U 0 without any position variables with values Um to with complete position values. The process uses forward checking for
 ; then the following three results may be obtained:
; then the following three results may be obtained:
-
No solution: meaning
 is inconsistent and Fis a contradictory allocation variable. F cannot be extended, which implies there is no position value for which an appropriate particle can be built, and an inappropriate particle is returned.
is inconsistent and Fis a contradictory allocation variable. F cannot be extended, which implies there is no position value for which an appropriate particle can be built, and an inappropriate particle is returned.
- With solution: meaning one single solution has been found. The algorithm terminates, and all the allocated position variable values are returned (i.e., one acceptable particle is returned).
- Unknown: meaning the particle filtering algorithm tries to create one single constraint to generate the position value of the next allocation and enlarge the set.
2.3. Rule Design for Classification Problem
2.3.1. Particle Encoding
In terms of particle encoding, we assign one particle as a rule set. The data are divided into continuous and discrete sets. Discrete data contain two SubParticles: (1) a flag denoting whether the attribute is Enabled/Disabled; (2) an attribute value. Continuous data have three SubParticles: (a) a flag denoting whether the attribute is Enabled/Disabled; (b) an operator; and (c) a value. The operator is either “≥” or “<.” [46T.F. Liang, and H.W. Cheng, "Multi-objective aggregate production planning decisions using two-phase fuzzy goal programming method", J. Ind. Manag. Optim., vol. 7, pp. 365-383, 2011.
[http://dx.doi.org/10.3934/jimo.2011.7.365] -48M.J. Alves, and J.P. Costa, "An algorithm based on particle swarm optimization for multiobjective bilevel linear problems", Appl. Math. Comput., vol. 247, pp. 547-561, 2014.
[http://dx.doi.org/10.1016/j.amc.2014.09.013] ]
In the encoding mode, Enable/Disable represents whether the attribute occurs in the rule condition, where the range value lies between 0 and 1. The first generation is randomly generated. If the value is less than 0.5, the attribute does not occur (Disable) in the rule condition. If the value is from 0.5–1.0, the attribute occurs (Enable) in the rule condition. The operator is the encoding format of continuous attributes, and its range value is 0–1. If the range value is 0–0.4, the operator of this attribute is <; otherwise, it is ≥, and the generated attribute value will not exceed the range values of the various attributes [34S. Validi, A. Bhattacharya, and P.J. Byrne, "Integrated low-carbon distribution system for the demand side of a product distribution supply chain: A DoE-guided MOPSO optimiser-based solution approach", Int. J. Prod. Res., vol. 52, pp. 3074-3096, 2014.
[http://dx.doi.org/10.1080/00207543.2013.864054] , 35J.J. Jamian, M.N. Abdullah, H. Mokhlis, M.W. Mustafa, and A.H. Bakar, "Global particle swarm optimization for high dimension numerical functions analysis", J. Appl. Math., vol. 2014, pp. 1-14, 2014.
[http://dx.doi.org/10.1155/2014/329193] ].
2.3.2. Fitness Evaluation
In this paper, each particle represents a set of classification rules. Thus, the fitness function of PSO is evaluated by the rate of satisfied classification rules. If there are rules and attributes, the complete rule set is as below and shown in Fig. (2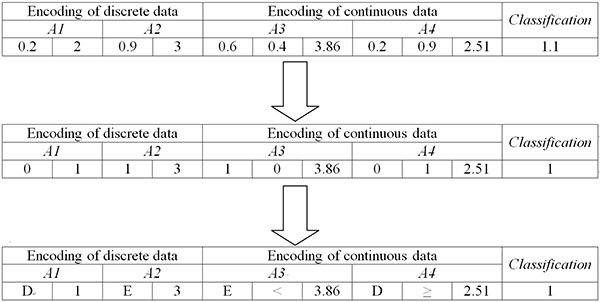 ), [26M.A. Villalobos-Arias, G.T. Pulido, and C.A. Coello, "A new mechanism to maintain diversity in multi-objective metaheuristics", Optimization, vol. 61, pp. 823-854, 2012.
), [26M.A. Villalobos-Arias, G.T. Pulido, and C.A. Coello, "A new mechanism to maintain diversity in multi-objective metaheuristics", Optimization, vol. 61, pp. 823-854, 2012.
[http://dx.doi.org/10.1080/02331934.2010.534476] , 27F. Jolai, R. Tavakkoli-Moghaddam, and M. Taghipour, "A multi-objective particle swarm optimisation algorithm for unequal sized dynamic facility layout problem with pickup/drop-off locations", Int. J. Prod. Res., vol. 50, pp. 4279-4293, 2012.
[http://dx.doi.org/10.1080/00207543.2011.613863] , 30F.J. Cabrerizo, E. Herrera-Viedma, and W. Pedrycz, "A method based on PSO and granular computing of linguistic information to solve group decision making problems defined in heterogeneous contexts", Eur. J. Oper. Res., vol. 230, pp. 624-633, 2013.
[http://dx.doi.org/10.1016/j.ejor.2013.04.046] ]:
 |
Fig. (2) Example for particle encoding. |
IF con1,1 And... And con1,n Then Class=C1
Else IF con2,1 And... And con2,n Then Class=C2
Else IF coni,1 And... And coni,n Then Class=Ci
Else IF conm,1 And... And conm,n Then Class=Cm
Else Unknown Classification Results
Rule = {If A2 = 3 AND A3 < 3.86 THEN Classification =1}
where coni,j is the jth attribute of the ith rule, and Ci is the classification result of the ith rule.
2.3.3. Stop Condition
The algorithm terminates when some maximum number of iterations is reached or the improvement efficiency is less than 2% over a number of executions. The maximum number of iterations was set to 300 in this study [34S. Validi, A. Bhattacharya, and P.J. Byrne, "Integrated low-carbon distribution system for the demand side of a product distribution supply chain: A DoE-guided MOPSO optimiser-based solution approach", Int. J. Prod. Res., vol. 52, pp. 3074-3096, 2014.
[http://dx.doi.org/10.1080/00207543.2013.864054] , 35J.J. Jamian, M.N. Abdullah, H. Mokhlis, M.W. Mustafa, and A.H. Bakar, "Global particle swarm optimization for high dimension numerical functions analysis", J. Appl. Math., vol. 2014, pp. 1-14, 2014.
[http://dx.doi.org/10.1155/2014/329193] ].
2.3.4. Particle Update Approach
In the traditional PSO update, the particle refers to individual and group optimum solutions, and uses a weight to update the velocity and then the position. As PSO and NSGAII use a fitness function to evaluate the classification rule, an increase in problem complexity tends to extend the search time, which may enable a local optimum to be attained. Thus, we propose novel update mechanisms for both PSO and the hybrid approach [46T.F. Liang, and H.W. Cheng, "Multi-objective aggregate production planning decisions using two-phase fuzzy goal programming method", J. Ind. Manag. Optim., vol. 7, pp. 365-383, 2011.
[http://dx.doi.org/10.3934/jimo.2011.7.365] -48M.J. Alves, and J.P. Costa, "An algorithm based on particle swarm optimization for multiobjective bilevel linear problems", Appl. Math. Comput., vol. 247, pp. 547-561, 2014.
[http://dx.doi.org/10.1016/j.amc.2014.09.013] ].
2.3.5. PSO Update Approach
In the PSO equations, each rule attribute has its initial execution speed and position. When the updated velocity is obtained by Eq. (30), the position is updated according to Eq. (31). The rule set is then updated to reflect the updated position, the particle is compared with the optimal rule set, and the rule attribute value of the same position is retained while the particle position is updated again. If the position is better than the previous individual optimum, the value is updated to Pid; if it is better than the group optimum, its value is updated to Pgd [46T.F. Liang, and H.W. Cheng, "Multi-objective aggregate production planning decisions using two-phase fuzzy goal programming method", J. Ind. Manag. Optim., vol. 7, pp. 365-383, 2011.
[http://dx.doi.org/10.3934/jimo.2011.7.365] -48M.J. Alves, and J.P. Costa, "An algorithm based on particle swarm optimization for multiobjective bilevel linear problems", Appl. Math. Comput., vol. 247, pp. 547-561, 2014.
[http://dx.doi.org/10.1016/j.amc.2014.09.013] ].
The difference between our approach and traditional PSO is that the optimal rule set is compared with each particle, and the same rule set is retained. The purpose of this is to keep the features of the optimal rule set so that each particle can retain its advantages. Thus, we are more likely to obtain the optimal rule set. Next, the validity of the rule set is guaranteed by applying the particle filtering algorithm. The rule set is input into the particle filtering algorithm to determine acceptable classification rules, and the particle fitness is recalculated and updated [30F.J. Cabrerizo, E. Herrera-Viedma, and W. Pedrycz, "A method based on PSO and granular computing of linguistic information to solve group decision making problems defined in heterogeneous contexts", Eur. J. Oper. Res., vol. 230, pp. 624-633, 2013.
[http://dx.doi.org/10.1016/j.ejor.2013.04.046] , 34S. Validi, A. Bhattacharya, and P.J. Byrne, "Integrated low-carbon distribution system for the demand side of a product distribution supply chain: A DoE-guided MOPSO optimiser-based solution approach", Int. J. Prod. Res., vol. 52, pp. 3074-3096, 2014.
[http://dx.doi.org/10.1080/00207543.2013.864054] , 35J.J. Jamian, M.N. Abdullah, H. Mokhlis, M.W. Mustafa, and A.H. Bakar, "Global particle swarm optimization for high dimension numerical functions analysis", J. Appl. Math., vol. 2014, pp. 1-14, 2014.
[http://dx.doi.org/10.1155/2014/329193] ].
2.3.6. Hybrid Approach
The hybrid update approach is illustrated in Fig. (3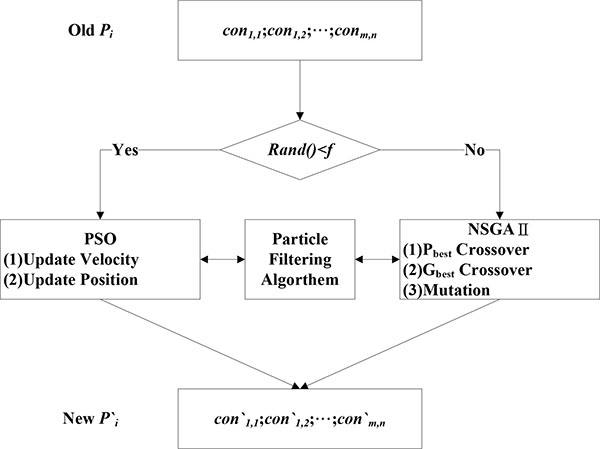 ), where the particle for executing NSGAII is selected from the proportion function f generated at random in the old swarm. The randomly selected particle is updated by the NSGAII approach, and a crossover between PBest and GBest is applied according to the fitness values of the particles. The mutation operator converts Enable into Disable, and the operator converts ≥ to <. In contrast, it is randomly generated, and the better fitness value replaces the old particle as the new particle. A swarm containing higher fitness values is obtained by this update mode, and this process is repeated until the stop condition is met [30F.J. Cabrerizo, E. Herrera-Viedma, and W. Pedrycz, "A method based on PSO and granular computing of linguistic information to solve group decision making problems defined in heterogeneous contexts", Eur. J. Oper. Res., vol. 230, pp. 624-633, 2013.
), where the particle for executing NSGAII is selected from the proportion function f generated at random in the old swarm. The randomly selected particle is updated by the NSGAII approach, and a crossover between PBest and GBest is applied according to the fitness values of the particles. The mutation operator converts Enable into Disable, and the operator converts ≥ to <. In contrast, it is randomly generated, and the better fitness value replaces the old particle as the new particle. A swarm containing higher fitness values is obtained by this update mode, and this process is repeated until the stop condition is met [30F.J. Cabrerizo, E. Herrera-Viedma, and W. Pedrycz, "A method based on PSO and granular computing of linguistic information to solve group decision making problems defined in heterogeneous contexts", Eur. J. Oper. Res., vol. 230, pp. 624-633, 2013.
[http://dx.doi.org/10.1016/j.ejor.2013.04.046] , 34S. Validi, A. Bhattacharya, and P.J. Byrne, "Integrated low-carbon distribution system for the demand side of a product distribution supply chain: A DoE-guided MOPSO optimiser-based solution approach", Int. J. Prod. Res., vol. 52, pp. 3074-3096, 2014.
[http://dx.doi.org/10.1080/00207543.2013.864054] , 35J.J. Jamian, M.N. Abdullah, H. Mokhlis, M.W. Mustafa, and A.H. Bakar, "Global particle swarm optimization for high dimension numerical functions analysis", J. Appl. Math., vol. 2014, pp. 1-14, 2014.
[http://dx.doi.org/10.1155/2014/329193] , 46T.F. Liang, and H.W. Cheng, "Multi-objective aggregate production planning decisions using two-phase fuzzy goal programming method", J. Ind. Manag. Optim., vol. 7, pp. 365-383, 2011.
[http://dx.doi.org/10.3934/jimo.2011.7.365] -48M.J. Alves, and J.P. Costa, "An algorithm based on particle swarm optimization for multiobjective bilevel linear problems", Appl. Math. Comput., vol. 247, pp. 547-561, 2014.
[http://dx.doi.org/10.1016/j.amc.2014.09.013] ].
 |
Fig. (3) Hybrid approach. |
3. COMPARISON OF DIFFERENT MULTI-OBJECTIVE ALGORITHMS AND CASE ANALYSIS
3.1. Comparison of Different Multi-objective Algorithms
The original NSGA sorts clusters according to the characteristics of non-dominance, and presents better non-dominated solutions with different fitness values according to the degree of domination. In the implementation of NSGA, solutions move toward the Pareto-optimal front. However, as no mechanism to retain differences among solutions has been proposed, the convergence of NSGA is often unstable, and the solution may be excessively concentrated within a single area. NSGAII sorts the population based on non-domination into each front. It includes a parameter called the ‘crowding distance,’ which measures how close an individual is to its neighbor solutions. This enables the search to be expanded while moving toward each front. After calculating the objective function, the population is sorted based on non-domination into each front. The first front is the ‘completely non-dominant set’ or ‘Pareto front’ [11K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, "A fast and elitist multi-objective genetic algorithm: NSGA-II", IEEE Trans. Evol. Comput., vol. 6, pp. 182-197, 2002.
[http://dx.doi.org/10.1109/4235.996017] , 34S. Validi, A. Bhattacharya, and P.J. Byrne, "Integrated low-carbon distribution system for the demand side of a product distribution supply chain: A DoE-guided MOPSO optimiser-based solution approach", Int. J. Prod. Res., vol. 52, pp. 3074-3096, 2014.
[http://dx.doi.org/10.1080/00207543.2013.864054] , 48M.J. Alves, and J.P. Costa, "An algorithm based on particle swarm optimization for multiobjective bilevel linear problems", Appl. Math. Comput., vol. 247, pp. 547-561, 2014.
[http://dx.doi.org/10.1016/j.amc.2014.09.013] ].
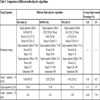
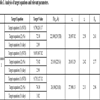
The results in (Table 1 and Fig. 4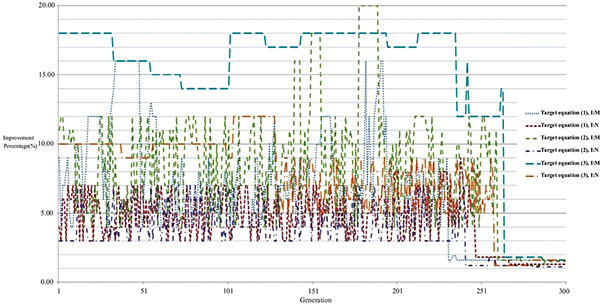 ) indicate that the proposed multi-objective algorithm outperforms the conventional MOPSO by expected total profit at least 6.36%, and exhibits an average improvement percentage of total market share of 3.71% over NSGAII. In these experiments, we set r = 28 (mm), Max Г0i(i) = 0.76(3), and θj(˚) = 16, as listed in Table 2.
) indicate that the proposed multi-objective algorithm outperforms the conventional MOPSO by expected total profit at least 6.36%, and exhibits an average improvement percentage of total market share of 3.71% over NSGAII. In these experiments, we set r = 28 (mm), Max Г0i(i) = 0.76(3), and θj(˚) = 16, as listed in Table 2.
3.2. Case Analysis
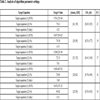
Table 3 presents a correlation analysis of the relevant parameters of a major cultural and creative company in Taiwan. There are two scenarios. The first scenario suggests that higher commodity prices (rijk) increase the total project cost
 and extend the completion time (z2), but result in lower customer evaluations (Sijk). The expected demand [Yi(rijk, hi)] and economic cyclical signals are not correlated. This may be because the commodity price can be raised, whereas commodity quality cannot be significantly improved. Hence, the demand of high-end customers cannot be satisfied, and customer evaluations suffer. In the second scenario, lower commodity prices (rijk) reduce the total project cost (
and extend the completion time (z2), but result in lower customer evaluations (Sijk). The expected demand [Yi(rijk, hi)] and economic cyclical signals are not correlated. This may be because the commodity price can be raised, whereas commodity quality cannot be significantly improved. Hence, the demand of high-end customers cannot be satisfied, and customer evaluations suffer. In the second scenario, lower commodity prices (rijk) reduce the total project cost (
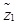 ) and shorten the completion time (z2), leading to higher customer evaluations (Sijk) and predicted demand Yi(rijk, hi), and better economic cyclical signals. Since the commodity price is lower, customers make lesser demands regarding quality, resulting in higher customer evaluations. It can be inferred that the customer commodity quality evaluation is unrelated to the commodity price (rijk) or predicted demand [Yi(rijk, hi)], and the economic cyclical signals are not related.
) and shorten the completion time (z2), leading to higher customer evaluations (Sijk) and predicted demand Yi(rijk, hi), and better economic cyclical signals. Since the commodity price is lower, customers make lesser demands regarding quality, resulting in higher customer evaluations. It can be inferred that the customer commodity quality evaluation is unrelated to the commodity price (rijk) or predicted demand [Yi(rijk, hi)], and the economic cyclical signals are not related.
 |
Fig. (4) Improvement Percentage convergence analysis of different algorithms. |
DISCUSSION
In the multi-target algorithm developed in this study, target equation (1) is better than MOPSO by 6.36% and NSGAII by 4.51%; target equation (2) is better than MOPSO by 8.13% and NSGAII by 3.71%; target equation (3) is better than MOPSO by 14.62% and NSGAII by 7.54%. Table (1) shows this clearly, thus demonstrating that the algorithm of this study is better than the others. According to Sections 2.2.1 and 2.2.2, a lower r (mm) is better; a higher Г0i is better; and a lower 0413;0i is better. The parameter setting of the algorithm is as follows: r (mm) is 28; ERS is 62; Г0i is 0.76; γ0i(k) is 6.84; θj(°˚) is 16. Table (2) shows the results. According to the analysis in Table (3), customers prefer cheap, but high-quality products. In particular, the products of cultural creativity have greater appeal to customers for their creative words or patterns. In comparison, the expensive and high-quality products of cultural creativity are less appealing to customers.
CONCLUSION AND FUTURE STUDIES
The proposed multi-objective algorithm outperforms conventional MOPSO and NSGAII. Our analysis has demonstrated that, when commodity prices are higher, the total project cost is higher and the completion time is longer. As a result, customer evaluations are lower. The expected demand and economic cyclical signals are not correlated, and Gross National Income (GNI) and Gross National Product (GNP) of parameters are ignored in this study. We believe that this may be because customers associate an increase in commodity price with a rise in commodity quality, although this cannot be significantly improved. Therefore, the demand of high-end customers cannot be satisfied, and customer evaluations become lower. When the commodity price is lower, the total project cost is lower and the completion time is shorter. Thus, customer evaluations are higher, the predicted demand is higher, and the economic cyclical signal is better. The lower commodity prices reduce customer demands on quality, resulting in higher customer evaluations. To summarize, the commodity quality evaluation made by customers has no bearing on commodity prices, and the predicted demand and economic cyclical signals are not related. In future studies, we aim to develop different multi-objective optimization models for different industries and improve the algorithms presented in this paper. Different multi-target problems will be evaluated in the future to find out which multi-target algorithm is better for seeking solutions. Updated multi-target algorithms will also be developed.
Vitae
Shen-Tsu Wang received his MS from the Department of Industrial Engineering and Management, National Yunlin University of Science and Technology, Taiwan in 2002. In 2008, he received his PhD from the Department of Industrial Engineering and Engineering Management, National Tsing Hua University, Taiwan. He is currently an Associate Professor at the Department of Commerce Automation and Management, National Pingtung University, Taiwan. His areas of interest include decision analysis and supply chain management.
APPENDIX
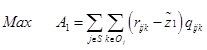 |
(1) |
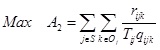 |
(2) |
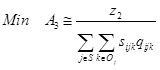 |
(3) |
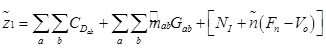 |
(4) |
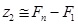 |
(5) |
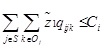 |
(6) |
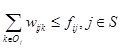 |
(7) |
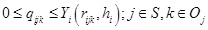 |
(8) |
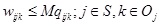 |
(9) |
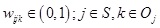 |
(10) |
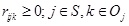 |
(11) |
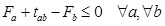 |
(12) |
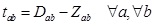 |
(13) |
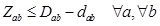 |
(14) |
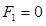 |
(15) |
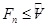 |
(16) |
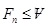 |
(17) |
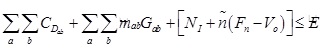 |
(18) |
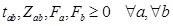 |
(19) |
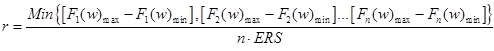 |
(20) |
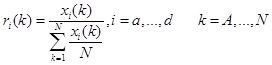 |
(21) |
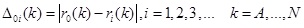 |
(22) |
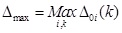 |
(23) |
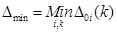 |
(24) |
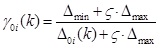 |
(25) |
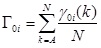 |
(26) |
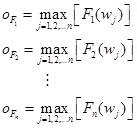 |
(27) |
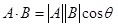 |
(28) |
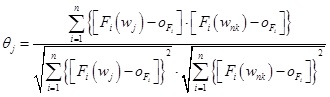 |
(29) |
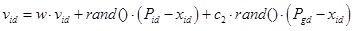 |
(30) |
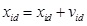 |
(31) |
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
FUNDING INFORMATION
None.
ACKNOWLEDGEMENTS
Declared none.
REFERENCES
| [1] | P. Holimchayachotikul, R. Derrouiche, D. Damand, and K. Leksakul, "Value creation through collaborative supply chain: holistic performance enhancement road map", Prod. Plann. Contr., vol. 25, pp. 912-922, 2014. [http://dx.doi.org/10.1080/09537287.2013.780313] |
| [2] | U. Schultze, E. Prandelli, P.I. Salonen, and M.V. Alstyne, "Internet-enabled co-production: partnering or competing with customers?", Commun. AIS, vol. 19, pp. 294-324, 2007. |
| [3] | E.V. Hippel, "Lead users: a source of novel product concepts", Manage. Sci., vol. 32, pp. 791-805, 2003. [http://dx.doi.org/10.1287/mnsc.32.7.791] |
| [4] | K.T. Hung, and H. Maleki, "Applying group technology to the forging industry", Prod. Plann. Contr., vol. 25, pp. 134-148, 2014. [http://dx.doi.org/10.1080/09537287.2013.782948] |
| [5] | J. Zhang, G.J. Tang, and Y.Z. Luo, "Hybrid multi-objective optimisation for concurrent activities consolidating two docked spacecraft", Int. J. Syst. Sci., vol. 46, pp. 2905-2917, 2015. [http://dx.doi.org/10.1080/00207721.2014.880198] |
| [6] | M.P. Biswal, and S. Acharya, "Multi-choice multi-objective mathematical programming model for integrated production planning: a case study", Int. J. Syst. Sci., vol. 44, pp. 1651-1665, 2013. [http://dx.doi.org/10.1080/00207721.2012.669862] |
| [7] | A. Žilinskas, "A statistical model-based algorithm for ‘black-box’ multi-objective optimization", Int. J. Syst. Sci., vol. 45, pp. 82-93, 2014. [http://dx.doi.org/10.1080/00207721.2012.702244] |
| [8] | J.L. Deng, "Control problems of grey systems", Syst. Control Lett., vol. 1, pp. 288-294, 1982. [http://dx.doi.org/10.1016/S0167-6911(82)80025-X] |
| [9] | R. Kowalczyk, "Using constraint satisfaction in genetic algorithms", Proc. Australian New Zealand Conf. Intell. Inf. Syst., 1996pp. 272-275 |
| [10] | N. Barnier, and P. Brisset, "Optimization by hybridization of a genetic algorithm and constraint satisfaction techniques", In: Proc. IEEE World Congr. Comput. Intell. Evol. Comput., 1998, pp. 645-649. [http://dx.doi.org/10.1109/ICEC.1998.700115] |
| [11] | K. Deb, A. Pratap, S. Agarwal, and T. Meyarivan, "A fast and elitist multi-objective genetic algorithm: NSGA-II", IEEE Trans. Evol. Comput., vol. 6, pp. 182-197, 2002. [http://dx.doi.org/10.1109/4235.996017] |
| [12] | C.A. Coello, G.T. Pulido, and M.S. Lechuga, "Handling multiple objectives with particle swarm optimization", IEEE Trans. Evol. Comput., vol. 8, pp. 256-279, 2004. [http://dx.doi.org/10.1109/TEVC.2004.826067] |
| [13] | S. Zhang, and K.W. Chau, Dimension Reduction Using Semi-Supervised Locally Linear Embedding for Plant Leaf Classification: ICIC'09 Proceedings of the 5th International Conference, Emerging Intelligent Computing Technology and Applications, September 16-19, 2009, Ulsan, South Korea, Springer: New York, 2009, pp. 948-955. |
| [14] | C.L. Wu, K.W. Chau, and Y.S. Li, "Methods to improve neural network performance in daily flows prediction", J. Hydro., vol. 372, pp. 80-93, 2009. [http://dx.doi.org/10.1016/j.jhydrol.2009.03.038] |
| [15] | K.W. Chau, and C.L. Wu, "A hybrid model coupled with singular spectrum analysis for daily rainfall prediction", J. Hydroinform., vol. 12, pp. 458-473, 2010. [http://dx.doi.org/10.2166/hydro.2010.032] |
| [16] | W.C. Wang, K.W. Chau, D.M. Xu, and X.Y. Chen, "Improving forecasting accuracy of annual runoff time series using ARIMA based on EEMD decomposition", Water Resour. Manage., vol. 29, pp. 2655-2675, 2015. [http://dx.doi.org/10.1007/s11269-015-0962-6] |
| [17] | N. Zeng, Z. Wang, Y. Li, M. Du, and X. Liu, "Identification of nonlinear lateral flow immunoassay state space models via particle filter approach", IEEE Trans. NanoTechnol., vol. 11, pp. 321-327, 2012. [http://dx.doi.org/10.1109/TNANO.2011.2171193] |
| [18] | C.J. Lin, and M.H. Hsieh, "Classification of mental task from EEG data using neural networks based on particle swarm optimization", Neurocomputing, vol. 72, pp. 1121-1130, 2009. [http://dx.doi.org/10.1016/j.neucom.2008.02.017] |
| [19] | C.K. Goh, K.C. Tan, D.S. Liu, and S.C. Chiam, "A competitive and cooperative co-evolutionary approach to multi-objective particle swarm optimization algorithm design", Eur. J. Oper. Res., vol. 202, pp. 42-54, 2010. [http://dx.doi.org/10.1016/j.ejor.2009.05.005] |
| [20] | S.J. Tsai, T.Y. Sun, C.C. Liu, S.T. Hsieh, W.C. Wu, and S.Y. Chiu, "An improved multi-objective particle swarm optimizer for multi-objective problems", Expert Syst. Appl., vol. 37, pp. 5872-5886, 2010. [http://dx.doi.org/10.1016/j.eswa.2010.02.018] |
| [21] | Y. Wang, and Y. Yang, "Particle swarm with equilibrium strategy of selection for multi-objective optimization", Eur. J. Oper. Res., vol. 200, pp. 187-197, 2010. [http://dx.doi.org/10.1016/j.ejor.2008.12.026] |
| [22] | A. Alcayde, R. Baños, C. Gil, F.G. Montoya, J. Moreno-Garcia, and J. Gómez, "Annealing-tabu PAES: a multi-objective hybrid meta-heuristic", Optimization, vol. 60, pp. 1473-1491, 2011. [http://dx.doi.org/10.1080/02331934.2010.505960] |
| [23] | T.Y. Sun, C.C. Liu, S.J. Tsai, S.T. Hsieh, and K.Y. Li, "Cluster guide particle swarm optimization (CGPSO) for underdetermined blind source separation with advanced conditions", IEEE Trans. Evol. Comput., vol. 15, pp. 798-811, 2011. [http://dx.doi.org/10.1109/TEVC.2010.2049361] |
| [24] | J.M. Yao, "Supply chain scheduling optimisation in mass customisation based on dynamic profit preference and application case study", Prod. Plann. Contr., vol. 22, pp. 690-707, 2011. [http://dx.doi.org/10.1080/09537287.2010.537577] |
| [25] | B. Fuchs, "Transforming lead user innovations into new corporate ventures: a matter of information asymmetry?", Int. J. Entrep. Innov. Manag., vol. 14, pp. 80-95, 2011. [http://dx.doi.org/10.1504/IJEIM.2011.040823] |
| [26] | M.A. Villalobos-Arias, G.T. Pulido, and C.A. Coello, "A new mechanism to maintain diversity in multi-objective metaheuristics", Optimization, vol. 61, pp. 823-854, 2012. [http://dx.doi.org/10.1080/02331934.2010.534476] |
| [27] | F. Jolai, R. Tavakkoli-Moghaddam, and M. Taghipour, "A multi-objective particle swarm optimisation algorithm for unequal sized dynamic facility layout problem with pickup/drop-off locations", Int. J. Prod. Res., vol. 50, pp. 4279-4293, 2012. [http://dx.doi.org/10.1080/00207543.2011.613863] |
| [28] | J. Zhang, and K.W. Chau, "Multilayer ensemble pruning via novel multi-sub-swarm particle swarm optimization", J. Univ. Compt. Sci., vol. 15, pp. 840-858, 2009. |
| [29] | R. Taormina, and K.W. Chau, "Data-driven input variable selection for rainfall–runoff modeling using binary-coded particle swarm optimization and extreme learning machines", J. Hydroinform., vol. 529, pp. 1617-1632, 2015. |
| [30] | F.J. Cabrerizo, E. Herrera-Viedma, and W. Pedrycz, "A method based on PSO and granular computing of linguistic information to solve group decision making problems defined in heterogeneous contexts", Eur. J. Oper. Res., vol. 230, pp. 624-633, 2013. [http://dx.doi.org/10.1016/j.ejor.2013.04.046] |
| [31] | D.C. Dang, R.N. Guibadj, and A. Moukrim, "An effective PSO-inspired algorithm for the team orienteering problem", Eur. J. Oper. Res., vol. 229, pp. 332-344, 2013. [http://dx.doi.org/10.1016/j.ejor.2013.02.049] |
| [32] | F.B. Ozsoydan, and A. Sipahioglu, "Heuristic solution approaches for the cumulative capacitated vehicle routing problem", Optimization, vol. 62, pp. 1321-1340, 2013. [http://dx.doi.org/10.1080/02331934.2013.841158] |
| [33] | J. Kou, S. Xiong, Z. Fang, X. Zong, and Z. Chen, "Multiobjective optimization of evacuation routes in stadium using superposed potential field network based ACO", Comput. Intell. Neurosci., vol. 2013, no. 369016, p. 369016, 2013. [PMID: 23861678] |
| [34] | S. Validi, A. Bhattacharya, and P.J. Byrne, "Integrated low-carbon distribution system for the demand side of a product distribution supply chain: A DoE-guided MOPSO optimiser-based solution approach", Int. J. Prod. Res., vol. 52, pp. 3074-3096, 2014. [http://dx.doi.org/10.1080/00207543.2013.864054] |
| [35] | J.J. Jamian, M.N. Abdullah, H. Mokhlis, M.W. Mustafa, and A.H. Bakar, "Global particle swarm optimization for high dimension numerical functions analysis", J. Appl. Math., vol. 2014, pp. 1-14, 2014. [http://dx.doi.org/10.1155/2014/329193] |
| [36] | M. Jakubcová, P. Máca, and P. Pech, "A comparison of selected modifications of the particle swarm optimization algorithm", J. Appl. Math., vol. 2014, pp. 1-10, 2014. [http://dx.doi.org/10.1155/2014/293087] |
| [37] | V. Osuna-Enciso, E. Cuevas, D. Oliva, V. Zúñiga, M. Pérez-Cisneros, and D. Zaldívar, "A multi-objective approach to homography estimation", Comput. Intell. Neurosci., vol. 2016, p. 3629174, 2016. [http://dx.doi.org/10.1155/2016/3629174] [PMID: 26839532] |
| [38] | N. Zeng, Z. Wang, Y. Li, M. Du, and X. Liu, "A hybrid EKF and switching PSO algorithm for joint state and parameter estimation of lateral flow immunoassay models", IEEE/ACM Trans. Comput. Biol. Bioinformatics, vol. 9, no. 2, pp. 321-329, 2012. [http://dx.doi.org/10.1109/TCBB.2011.140] [PMID: 22025755] |
| [39] | N. Zeng, Y.S. Hung, Y. Li, and M. Du, "A novel switching local evolutionary PSO for quantitative analysis of lateral flow immunoassay", Expert Syst. Appl., vol. 41, pp. 1708-1715, 2014. [http://dx.doi.org/10.1016/j.eswa.2013.08.069] |
| [40] | N. Zeng, Z. Wang, H. Zhang, and F.E. Alsaadi, "A novel switching delayed PSO algorithm for estimating unknown parameters of lateral flow immunoassay", Cognit. Comput., vol. 8, pp. 143-152, 2016. [http://dx.doi.org/10.1007/s12559-016-9396-6] |
| [41] | N. Zeng, H. Zhang, Y. Chen, B. Chen, and Y. Liu, "Path planning for intelligent robot based on switching local evolutionary PSO algorithm", Assem. Autom., vol. 36, pp. 120-126, 2016. [http://dx.doi.org/10.1108/AA-10-2015-079] |
| [42] | W. Li, C. Zhao, and D. Li, "Flowshop with multiple processors dynamic scheduling problem based on hybrid genetic-particle swarm optimization", Open Cybernet. Sys. J., vol. 9, pp. 1038-1044, 2015. |
| [43] | L. Chen, "The chaotic EM algorithm based on the L-BFGS operator and its application in the path optimization", Open Cybernet. Sys. J., vol. 9, pp. 501-507, 2015. |
| [44] | N. Tao, G. Chen, R. Chen, and H. Jin, "A novel hybrid method for solving flexible job-shop scheduling problem", Open Cybernet. Sys. J., vol. 10, pp. 13-19, 2016. |
| [45] | T.F. Liang, "Fuzzy multi-objective project management decisions using two-phase fuzzy goal programming approach", Comput. Ind. Eng., vol. 57, pp. 1407-1416, 2009. [http://dx.doi.org/10.1016/j.cie.2009.07.010] |
| [46] | T.F. Liang, and H.W. Cheng, "Multi-objective aggregate production planning decisions using two-phase fuzzy goal programming method", J. Ind. Manag. Optim., vol. 7, pp. 365-383, 2011. [http://dx.doi.org/10.3934/jimo.2011.7.365] |
| [47] | B. Nadel, "Tree search and arc consistency in constraint satisfaction algorithms", In: L. Kanal, and V. Kumar, Eds., Search in Artificial Intelligence., Springer-Verlag: New York, 1998, pp. 287-342. |
| [48] | M.J. Alves, and J.P. Costa, "An algorithm based on particle swarm optimization for multiobjective bilevel linear problems", Appl. Math. Comput., vol. 247, pp. 547-561, 2014. [http://dx.doi.org/10.1016/j.amc.2014.09.013] |
| [49] | A.P. Dharshini, S. Chandrakumarmangalam, and G. Arthi, "Ant colony optimization for competency based learning objects sequencing in e-learning", Appl. Math. Comput., vol. 263, pp. 332-341, 2015. [http://dx.doi.org/10.1016/j.amc.2015.04.067] |
| [50] | Y.B. Shin, and E. Kita, "Search performance improvement of particle swarm optimization by second best particle information", Appl. Math. Comput., vol. 246, pp. 346-354, 2014. [http://dx.doi.org/10.1016/j.amc.2014.08.013] |
| [51] | M.A. Peteraf, and J.B. Barney, "Unraveling the resource-based tangle", Manage. Decis. Econ., vol. 24, pp. 309-323, 2003. [http://dx.doi.org/10.1002/mde.1126] |
| [52] | N. Srinivas, and K. Deb, "Multi-objective optimization using non-dominated sorting in genetic algorithms", Evol. Comput., vol. 2, pp. 221-248, 1994. [http://dx.doi.org/10.1162/evco.1994.2.3.221] |