- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Cybernetics & Systemics Journal
(Discontinued)
ISSN: 1874-110X ― Volume 12, 2018
Optimizing Preventive Maintenance of Used Equipment for Lease Using Enumeration Algorithm
Fengshou Qian, Ke Dong*
Abstract
Background:
With the progress of technology and people's awareness of environmental protection, more and more used equipment flows into the market. But the lessee is most concerned about the functionality and reliability of the equipment, because fault downtime and repair will lead to the loss of production.
Objective:
In order to solve this problem, we propose a maintenance scheme for the used equipment using fixed failure rate reduction method.
Method:
An efficient enumeration algorithm is given to derive the optimal PM policy.
Results:
In case study, the proposed policy is compared with the performance of other approach through examples.
Conclusions:
Numerical examples illustrate that the proposed maintenance strategy is practical and it can provide effective decision support for leasing company.
Article Information
Identifiers and Pagination:
Year: 2017Volume: 11
First Page: 86
Last Page: 93
Publisher Id: TOCSJ-11-86
DOI: 10.2174/1874110X01711010085
Article History:
Received Date: 16/10/2016Revision Received Date: 29/12/2016
Acceptance Date: 27/01/2017
Electronic publication date: 28/04/2017
Collection year: 2017
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: (https://creativecommons.org/licenses/by/4.0/legalcode). This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
* Address correspondence to this author at the School of Economics and Management, Anhui Radio & TV University, 398 Tongcheng Rd, Hefei, 230022, China; Tel: 13721054899, 13339011752; E-mail: dongke@ahtvu.ah.cn
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 16-10-2016 |
Original Manuscript | Optimizing Preventive Maintenance of Used Equipment for Lease Using Enumeration Algorithm | |
1. INTRODUCTION
Recycling and reusing of a used equipment has significant potential for reducing environmental impacts, and protects the environment by preventing the used equipment from becoming waste. On the other hand, from the perspective of the lessor, they can lease the equipment to other lessees to obtain maximum profits from the used equipment. But the lessee is most concerned about the functionality and reliability of the equipment, because fault downtime and repair will lead to the loss of production. In the lease contract, the lessor incurs a penalty for each failure that occurs over the lease period or the time to repair the failure exceeds pre-specified time. Therefore, the lessor adopts preventive maintenance (PM) actions to reduce the failure number and slow down the equipment degradation.
In general, there are two categories for maintenance actions considered in a lease contract: corrective maintenance (CM) and preventive maintenance (PM). CM means all actions performed to restore an item to a specified condition, whereas PM is the maintenance that occurs when a system is operating, thereby decreasing the likelihood of equipment failure. Various maintenance policies have been extensively discussed in the literature [1R. Barlow, and L. Hunter, "Optimum preventive maintenance policies", Oper. Res., vol. 8, no. 1, pp. 90-100, 1960.
[http://dx.doi.org/10.1287/opre.8.1.90] -5T. Nakagawa, "A summary of periodic replacement with minimal repair at failure", J. Oper. Res. Soc. Jpn., vol. 24, no. 3, pp. 213-228, 1981.]. For corrective maintenance, minimal repair is most commonly adopted to restore failed equipment [6T. Nakagawa, and M. Kowada, "Analysis of a system with minimal repair and its application to replacement policy", Eur. J. Oper. Res., vol. 12, no. 2, pp. 176-182, 1983.
[http://dx.doi.org/10.1016/0377-2217(83)90221-7] , 7V. Jayabalan, and D. Chaudhuri, "Optimal maintenance and replacement policy for a deteriorating system with increased mean downtime", Nav. Res. Log., vol. 39, no. 1, pp. 67-78, 1992.
[http://dx.doi.org/10.1002/1520-6750(199202)39:1<67::AID-NAV3220390106>3.0.CO;2-2] ]. After minimal repair, the equipment is restored in the normal operation. However, the failure rate of the equipment remains unchanged.
To reduce the number of failures and possible penalties within the lease period, most lessors undertake PM actions. Numerous PM policies have been proposed and studied for different situations, such as finite or infinite horizon [8R.H. Yeh, and C.K. Chen, "Periodical preventive-maintenance contract for a leased facility with Weibull life-time", Qual. Quant., vol. 40, no. 2, pp. 303-313, 2006.
[http://dx.doi.org/10.1007/s11135-005-8095-2] ], periodic or sequential maintenance [6T. Nakagawa, and M. Kowada, "Analysis of a system with minimal repair and its application to replacement policy", Eur. J. Oper. Res., vol. 12, no. 2, pp. 176-182, 1983.
[http://dx.doi.org/10.1016/0377-2217(83)90221-7] , 9T. Nakagawa, and S. Mizutani, "A summary of maintenance policies for a finite interval", Reliab. Eng. Syst. Saf., vol. 94, no. 1, pp. 89-96, 2009.
[http://dx.doi.org/10.1016/j.ress.2007.04.004] ], and perfect or imperfect maintenance [2H. Pham, and H. Wang, "Imperfect maintenance", Eur. J. Oper. Res., vol. 94, no. 3, pp. 425-438, 1996.
[http://dx.doi.org/10.1016/S0377-2217(96)00099-9] ]. For the imperfect PM actions, two methods have been studied [6T. Nakagawa, and M. Kowada, "Analysis of a system with minimal repair and its application to replacement policy", Eur. J. Oper. Res., vol. 12, no. 2, pp. 176-182, 1983.
[http://dx.doi.org/10.1016/0377-2217(83)90221-7] ]: (1) age-reduction method (ARM), in which the degree of PM action is described by the reduction in the duration of the equipment, and (2) failure rate reduction method (FRRM), in which the failure rate of the equipment is reduced after each PM action. As to the two methods mentioned, we can find detailed description from these literatures [10R.H. Yeh, and H.C. Lo, "Optimal preventive-maintenance warranty policy for repairable products", Eur. J. Oper. Res., vol. 134, no. 1, pp. 59-69, 2001.
[http://dx.doi.org/10.1016/S0377-2217(00)00238-1] -12J. Jaturonnatee, D.N. Murthy, and R. Boondiskulchok, "Optimal preventive maintenance of leased equipment with corrective minimal repairs", Eur. J. Oper. Res., vol. 174, no. 1, pp. 201-215, 2006.
[http://dx.doi.org/10.1016/j.ejor.2005.01.049] ].
But all of the above-mentioned references are studied the new equipment. The literature is scant about used equipment. Chattopadhyay and Murthy [13G.N. Chattopadhyay, and D.N. Murthy, "Warranty cost analysis for second-hand products", Math. Comput. Model., vol. 31, no. 10, pp. 81-88, 2000.
[http://dx.doi.org/10.1016/S0895-7177(00)00074-1] ] proposed a model to estimate the expected warranty cost for second-hand products sold with free replacements or pro rata warranty policies, but they did not consider PM action. Pongpech, Murthy and Boondiskulchock [3J. Pongpech, and D.N. Murthy, "Optimal periodic preventive maintenance policy for leased equipment", Reliab. Eng. Syst. Saf., vol. 91, no. 7, pp. 772-777, 2006.
[http://dx.doi.org/10.1016/j.ress.2005.07.005] ] proposed a model for the lease contract of used equipment, but there are (2k+2) parameters that need to be selected optimally. Yeh, Lo and Yu [14R.H. Yeh, and H.C. Lo, "H, and R. Y. Yu, “A study of maintenance policies for second-hand products", Comput. Ind. Eng., vol. 60, no. 3, pp. 438-444, 2011.
[http://dx.doi.org/10.1016/j.cie.2010.07.033] ] (henceforth referred to as policy Y) proposed a model for second-hand products, but it focused on the maintenance strategies when a user buys a second-hand product. We present a preventive maintenance policy with failure rate reduction(referred to as policy D). Under our approach, the PM actions are performed sequentially with a fixed maintenance degree. As we will see later on, the performance of the proposed maintenance scheme is better than Yeh’s scheme [14R.H. Yeh, and H.C. Lo, "H, and R. Y. Yu, “A study of maintenance policies for second-hand products", Comput. Ind. Eng., vol. 60, no. 3, pp. 438-444, 2011.
[http://dx.doi.org/10.1016/j.cie.2010.07.033] ], and when the initial duration value is zero, the model is the same as the maintenance model [15R.H. Yeh, K.C. Kao, and W.L. Chang, "Optimal preventive maintenance policy for leased equipment using failure rate reduction", Comput. Ind. Eng., vol. 57, no. 1, pp. 304-309, 2009.
[http://dx.doi.org/10.1016/j.cie.2008.11.025] ].
The remainder of this paper is organized as follows. The mathematical model is developed in section 2. In section 3, the optimal PM policy is derived and an efficient algorithm is proposed for Weibull distribution of used equipment. In section 4, the impact of providing preventive maintenance is illustrated through numerical examples, and gives a comparison with the maintenance scheme of Yeh [14R.H. Yeh, and H.C. Lo, "H, and R. Y. Yu, “A study of maintenance policies for second-hand products", Comput. Ind. Eng., vol. 60, no. 3, pp. 438-444, 2011.
[http://dx.doi.org/10.1016/j.cie.2010.07.033] ]. Finally, conclusions are drawn in section 5.
2. MATHEMATICAL FORMULATION
Consider that an equipment with Weibull lifetime distribution is leased at age A and intended to be leased for a period of L. The failure rate function of the Weibull distribution is given by
 |
(1) |
Where α is called the scale parameter and β is called the shape parameter. The inverse function of λ(t) is given by
 |
(2) |
Note that both λ(t) and its inverse function λ-1(t) increase in t when the shape parameter β > 1, and decrease in t when β > 1. In this article, we focus on the case where failure rate function λ(t) continuously increases in t and λ-1(t) exists (i.e. β > 1) within the lease period.
Within the lease period, any failure of the leased equipment is repaired using minimal repair by the lessor with a fixed repair cost Cm and the lessor incurs a penalty cost Cn (we call penalty 1) for each failure that occurs over the lease period. After minimal repair, the equipment is operational, but the failure rate of the equipment remains the same as that just before failure. It is assumed that each failure requires a random amount of repair time t which is subject to a general cumulative distribution function G(t). Furthermore, if the repair time exceeds a pre-specified time limit τ, there is a penalty cost Cτ (we call penalty 2) to the lessor.
To reduce the number of possible failures over the lease period, n PM actions are carried out at time epoch ti, where A=tO < t1 < t2 < ... < tn < L + A. After the PM actions, the failure rate of the equipment is reduced by a fixed amount δ ≥ 0. In general, the cost to perform a PM action is a non-negative and non-decreasing function of the maintenance degree δ. In this paper, we consider the case where the PM cost Cp (δ) is a linearly increasing function of the maintenance degree δ; that is, Cp (δ)= a+b (δ) for any a > 0, b > 0. It is assumed that the time required for performing PM actions is negligible. After the ith PM action, the PM failure intensity becomes λ0 (ti-A)-iδ for all i=1,2,...,n as shown in Fig. (1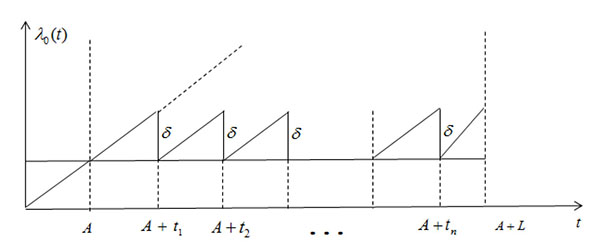 ).
).
 |
Fig. (1) Optimal PM policy under fixed failure rate reduction. |
The expected number of failures over the lease period, with the proposed PM actions, is given by
 |
(3) |
Define  , then Eq. (3) is equivalent to
, then Eq. (3) is equivalent to
 |
(4) |
Where  denotes the vector of time epochs to perform PM actions.
denotes the vector of time epochs to perform PM actions.
The expected total cost within the lease period L including minimal repair cost, penalty cost, and PM cost which can be easily obtained as follows:
 |
(5) |
Define  , and substitute (4) into (5), then (5) can be rewritten as
, and substitute (4) into (5), then (5) can be rewritten as
 |
(6) |
Note that there are n=3 decision variables including the number of PM actions n, PM degree δ, and the time epochs ti. Hence, our objective here is to find an optimal PM policy  such that the expected total cost in Eq. (6) is minimized.
such that the expected total cost in Eq. (6) is minimized.
3. OPTIMAL PM POLICY
Now we will give a theorem that shows the relationship between the optimal time epoch  and the inverse failure rate function
and the inverse failure rate function  in Eq. (2).
in Eq. (2).
Theorem 1. Given any n > 0 and δ > 0, if λO(t) is a strictly increasing function of t when β > 1, then  .
.
Proof.
Given any n > 0 and δ > 0, we have  , for all i=1,2,...,n. This result indicates that
, for all i=1,2,...,n. This result indicates that  is an increasing function of δ, and implies that to minimize
is an increasing function of δ, and implies that to minimize  is equivalent to minimize
is equivalent to minimize  , since Cp(δ), L and C´ are all constants. Therefore, ti should take the minimum value which is subject to the constraint λ (ti-A)-iδ ≥ 0 for all i=1,2,...,n. Since λ0 (t) is a strictly increasing function of t, we obtain
, since Cp(δ), L and C´ are all constants. Therefore, ti should take the minimum value which is subject to the constraint λ (ti-A)-iδ ≥ 0 for all i=1,2,...,n. Since λ0 (t) is a strictly increasing function of t, we obtain  . Hence, the minimal value of
. Hence, the minimal value of  is obtained at
is obtained at  for all i=1,2,...,n.
for all i=1,2,...,n.
Theorem 1 shows that optimal value of  is that
is that  , with this, the objective function becomes
, with this, the objective function becomes
 |
(7) |
There are only two decision variables n and δ to be determined. In order to find the optimal value of n* and δ*, we suppose that n is given and we find the optimal value δ*. After we find the optimal value δ*, the value n can be obtained by any search method directly.
In Eq. (7), if  is an increasing function, there is no need to perform PM actions. Therefore, we will focus on the situation that
is an increasing function, there is no need to perform PM actions. Therefore, we will focus on the situation that  . Given any n > 0, the theorem below shows that if it satisfies some reasonable conditions, there exists a unique closed-form solution of δ* such that the expected total cost is minimized.
. Given any n > 0, the theorem below shows that if it satisfies some reasonable conditions, there exists a unique closed-form solution of δ* such that the expected total cost is minimized.
Theorem 2. Given any n > 0, if the failure intensity function is subject to Weibull distribution, then the following results hold:
(1) If  , then δ*=0;
, then δ*=0;
(2) If  , and
, and  ,then there exists
,then there exists  .
.
Given any n > 0, the first and second partial derivatives of Eq. (7) with respect to δ, we have
 |
(8) |
 |
(9) |
We know that the inverse function  is strictly increasing in (iδ), so
is strictly increasing in (iδ), so  for all i. Hence, when
for all i. Hence, when  , Eq. (8) is positive for all δ which implies that
, Eq. (8) is positive for all δ which implies that  is strictly increasing function of δ for any n > 0. In this case, the optimal maintenance degree δ* is zero.
is strictly increasing function of δ for any n > 0. In this case, the optimal maintenance degree δ* is zero.
On the other hand, if  , we obtain
, we obtain  and
and  . When
. When  , then Eq. (9) is positive for all δ. In this case, Eq. (8) is a strictly increasing function of δ and changes its sign at most once from negative to positive. Therefore, there exists a unique δ* > 0, such that
, then Eq. (9) is positive for all δ. In this case, Eq. (8) is a strictly increasing function of δ and changes its sign at most once from negative to positive. Therefore, there exists a unique δ* > 0, such that  . Furthermore, given any n > 0, there is an upper bound of δ, which is
. Furthermore, given any n > 0, there is an upper bound of δ, which is  . Hence, if
. Hence, if  , then
, then  ; otherwise,
; otherwise, 
For the Weibull case with any n > 0, Eq. (7) becomes
 |
(10) |
where  . We take the first derivative of Eq. (10) with respect to δ we obtain
. We take the first derivative of Eq. (10) with respect to δ we obtain
 |
(11) |
If  , from the derivation above, we know that Eq. (10) is positive. Hence, the PM action is not necessary. When
, from the derivation above, we know that Eq. (10) is positive. Hence, the PM action is not necessary. When  , and
, and  , let Eq. (11) equal to zero, we obtain the optimal δ:
, let Eq. (11) equal to zero, we obtain the optimal δ:
 |
Using the result of theorem 2 above, the optimal maintenance degree δ* can be obtained easily. Now, there is only one decision variable n which represents the optimal number of the PM actions within the leased period to be determined. In order to find the optimal expected total cost, we use enumeration algorithm. Without loss of generality, we may set  or any other large number and search the optimal value of n from 0 to
or any other large number and search the optimal value of n from 0 to  . The following algorithm provides an efficient search procedure for deriving the optimal policy
. The following algorithm provides an efficient search procedure for deriving the optimal policy  .
.
Step 1: if  , then
, then  , and stop.
, and stop.
Step 2: set  or any large number, and n=1.
or any large number, and n=1.
step 3:  , such that we obtain
, such that we obtain  .
.
Step 4: if  , then set
, then set  , and
, and  .
.
Step 5: if  , then stop; otherwise, set n=n+1 and go to step 3.
, then stop; otherwise, set n=n+1 and go to step 3.
4. NUMERICAL EXAMPLES
In this section, the performance of the proposed optimal PM policy is evaluated through numerical examples.
4.1. Numerical Results Under Fixed Failure Rate Reduction
We assume that the failure distribution for the used equipment(for example: used cars, used computers) is given by the two-parameter Weibull distribution with scale parameter α=1 and the shape parameter β > 1 which implies that the failure rate is increasing. We suppose that repair time t is subject to a two-parameter Weibull distribution (2,0.5). If the repair time exceeds τ=2, then there is a penalty cost Cτ = 300per unit time to the lessor. Then, we obtain the total expected cost to the lessor at each failure is  , and the cost for performing a PM action with maintenance degree δ is a linear function Cp(δ)=100+50δ. We consider used equipment with age A is planned to be leased for a period of L = 3 years. To evaluate the performance of the proposed optimal PM policy, we use C0 denoted the expected total cost without PM actions, and define
, and the cost for performing a PM action with maintenance degree δ is a linear function Cp(δ)=100+50δ. We consider used equipment with age A is planned to be leased for a period of L = 3 years. To evaluate the performance of the proposed optimal PM policy, we use C0 denoted the expected total cost without PM actions, and define  to denote the percentage of cost reduction, where C* denotes the optimal expected total cost. (Table 1) summarizes the numerical results for various combinations of β,A,Cn,Cτ.
to denote the percentage of cost reduction, where C* denotes the optimal expected total cost. (Table 1) summarizes the numerical results for various combinations of β,A,Cn,Cτ.
From (Table 1), we make some interesting observations:
- When A=0, the results are the same as the maintenance model [15R.H. Yeh, K.C. Kao, and W.L. Chang, "Optimal preventive maintenance policy for leased equipment using failure rate reduction", Comput. Ind. Eng., vol. 57, no. 1, pp. 304-309, 2009.
[http://dx.doi.org/10.1016/j.cie.2008.11.025] ], the model in this paper degenerates to the model in their paper. - As A increases, C0 and C* increase, but the percentage of cost reduction
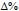 decreases. This result implies that the PM actions have little impact on the expected cost with the duration of the used equipment increasing.
decreases. This result implies that the PM actions have little impact on the expected cost with the duration of the used equipment increasing.
- As β increases, both the optimal number of PM actions n* and the optimal maintenance degree δ* increase.
- As penalty 1 increases, the optimal expected total cost C* increases, the optimal number of PM actions n* increases, and the percentage of cost reduction
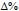 also increases which implies that there is a significant impact in the PM actions on the expected cost when the lease period is relatively long. The situations of penalty 2, penalty 1 and penalty 2 combined are similar to penalty 1.
also increases which implies that there is a significant impact in the PM actions on the expected cost when the lease period is relatively long. The situations of penalty 2, penalty 1 and penalty 2 combined are similar to penalty 1.
4.2. Comparisons
In this section, the performance of the optimal policies in this paper is compared with the model I in Yeh [14R.H. Yeh, and H.C. Lo, "H, and R. Y. Yu, “A study of maintenance policies for second-hand products", Comput. Ind. Eng., vol. 60, no. 3, pp. 438-444, 2011.
[http://dx.doi.org/10.1016/j.cie.2010.07.033] ] (policy Y).
We consider that used equipment will be leased at age A for a lease period L=5. We assume the each minimal repair cost Cm=100, Cn=Cτ=0, and the cost for performing a PM action with maintenance degree δ is a linear function Cp(δ)=100+50 δ. With loss of generality, we suppose α = 1. In comparison with the results of Yeh’s policy [13G.N. Chattopadhyay, and D.N. Murthy, "Warranty cost analysis for second-hand products", Math. Comput. Model., vol. 31, no. 10, pp. 81-88, 2000.
[http://dx.doi.org/10.1016/S0895-7177(00)00074-1] ], we set  .
.
(Table 2) lists and compares the two policies. From (Table 2), we make the following observations:
(1) When β = 1.2, there is no need to perform PM actions for policy Y, policy D has better performance at this time.
(2) When β = 1.2 and A with different values, the optimal number of PM actions n* is the same between the two policies, but policy D also has better performance than policy Y.
CONCLUSION
Under the failure rate reduction method, we propose a maintenance scheme for used equipment and derive the optimal PM policy for used equipment. From the numerical examples, we find that the performance of the optimal policy with fixed maintenance degree is better than the periodical policy with fixed maintenance interval, and when the initial value of the duration is zero, the model is degenerated to the form of Yeh’s [14R.H. Yeh, and H.C. Lo, "H, and R. Y. Yu, “A study of maintenance policies for second-hand products", Comput. Ind. Eng., vol. 60, no. 3, pp. 438-444, 2011.
[http://dx.doi.org/10.1016/j.cie.2010.07.033] ].
The proposed model can be extended in several ways, such as the cost of minimal repair increase with duration of equipment, non-linear maintenance cost, time-dependent penalty cost, or various penalty schemes. We are currently interested in some of these topics.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
This research is supported the Key Program of Anhui Humanities and Social Science, (No. SK2015A649), Nature Science (KJ2017A941), China.
REFERENCES
| [1] | R. Barlow, and L. Hunter, "Optimum preventive maintenance policies", Oper. Res., vol. 8, no. 1, pp. 90-100, 1960. [http://dx.doi.org/10.1287/opre.8.1.90] |
| [2] | H. Pham, and H. Wang, "Imperfect maintenance", Eur. J. Oper. Res., vol. 94, no. 3, pp. 425-438, 1996. [http://dx.doi.org/10.1016/S0377-2217(96)00099-9] |
| [3] | J. Pongpech, and D.N. Murthy, "Optimal periodic preventive maintenance policy for leased equipment", Reliab. Eng. Syst. Saf., vol. 91, no. 7, pp. 772-777, 2006. [http://dx.doi.org/10.1016/j.ress.2005.07.005] |
| [4] | H. Wang, "A survey of maintenance policies of deteriorating systems", Eur. J. Oper. Res., vol. 139, no. 3, pp. 469-489, 2002. [http://dx.doi.org/10.1016/S0377-2217(01)00197-7] |
| [5] | T. Nakagawa, "A summary of periodic replacement with minimal repair at failure", J. Oper. Res. Soc. Jpn., vol. 24, no. 3, pp. 213-228, 1981. |
| [6] | T. Nakagawa, and M. Kowada, "Analysis of a system with minimal repair and its application to replacement policy", Eur. J. Oper. Res., vol. 12, no. 2, pp. 176-182, 1983. [http://dx.doi.org/10.1016/0377-2217(83)90221-7] |
| [7] | V. Jayabalan, and D. Chaudhuri, "Optimal maintenance and replacement policy for a deteriorating system with increased mean downtime", Nav. Res. Log., vol. 39, no. 1, pp. 67-78, 1992. [http://dx.doi.org/10.1002/1520-6750(199202)39:1<67::AID-NAV3220390106>3.0.CO;2-2] |
| [8] | R.H. Yeh, and C.K. Chen, "Periodical preventive-maintenance contract for a leased facility with Weibull life-time", Qual. Quant., vol. 40, no. 2, pp. 303-313, 2006. [http://dx.doi.org/10.1007/s11135-005-8095-2] |
| [9] | T. Nakagawa, and S. Mizutani, "A summary of maintenance policies for a finite interval", Reliab. Eng. Syst. Saf., vol. 94, no. 1, pp. 89-96, 2009. [http://dx.doi.org/10.1016/j.ress.2007.04.004] |
| [10] | R.H. Yeh, and H.C. Lo, "Optimal preventive-maintenance warranty policy for repairable products", Eur. J. Oper. Res., vol. 134, no. 1, pp. 59-69, 2001. [http://dx.doi.org/10.1016/S0377-2217(00)00238-1] |
| [11] | J. Pongpech, D.N. Murthy, and R. Boondiskulchock, "Maintenance strategies for used equipment under lease", J. Qual. Mainten. Eng., vol. 12, no. 1, pp. 52-67, 2006. [http://dx.doi.org/10.1108/13552510610654538] |
| [12] | J. Jaturonnatee, D.N. Murthy, and R. Boondiskulchok, "Optimal preventive maintenance of leased equipment with corrective minimal repairs", Eur. J. Oper. Res., vol. 174, no. 1, pp. 201-215, 2006. [http://dx.doi.org/10.1016/j.ejor.2005.01.049] |
| [13] | G.N. Chattopadhyay, and D.N. Murthy, "Warranty cost analysis for second-hand products", Math. Comput. Model., vol. 31, no. 10, pp. 81-88, 2000. [http://dx.doi.org/10.1016/S0895-7177(00)00074-1] |
| [14] | R.H. Yeh, and H.C. Lo, "H, and R. Y. Yu, “A study of maintenance policies for second-hand products", Comput. Ind. Eng., vol. 60, no. 3, pp. 438-444, 2011. [http://dx.doi.org/10.1016/j.cie.2010.07.033] |
| [15] | R.H. Yeh, K.C. Kao, and W.L. Chang, "Optimal preventive maintenance policy for leased equipment using failure rate reduction", Comput. Ind. Eng., vol. 57, no. 1, pp. 304-309, 2009. [http://dx.doi.org/10.1016/j.cie.2008.11.025] |





