- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Cybernetics & Systemics Journal
(Discontinued)
ISSN: 1874-110X ― Volume 12, 2018
Medical Decision Making via the Arithmetic of Generalized Triangular Fuzzy Numbers
Palash Dutta1, *, Satya Ranjan Dash2
Abstract
Background:
When patient(s) approach to a medical expert to explain their problems, they often explain their conditions through vague linguistic expression [1]. Medical expert needs to prepare a list of potential symptoms for the particular diseases of the patients based on their vague linguistic statements. Together with the vagueness in medical documents and imprecise information gathered for decision making makes the medical experts’ job more complex. Due to the occurrence of uncertainty in medical decision making exploitation of the Fuzzy Set (FST) is required. Generally in literature, type-I fuzzy set, Intuitionistic Fuzzy Sets (IFSs), Interval Valued Fuzzy Sets (IVFSs), and Picture Fuzzy Sets (PFSs) are extensively applied in medical decision making.
Objective:
Although different approaches have been used in medical decision making, no single evidence has been observed in use of Generalized Fuzzy Numbers (GFNs) in medical decision making. GFN has the ability to deal with vague/imprecise information in a supple way. Basically, the parameter height of GFN characterizes the grade of buoyancy of judgments of decision takers in a very specific comportment. Therefore, a maiden effort has been made to study medical diagnosis using arithmetic of GFNs, and finally to exhibit the techniques a case study has been carried out under this setting.
Method:
To achieve the proposed goal an algorithm is being formulated and to obtain patients-diseases relationship the arithmetic of GFNs is used as the composition of fuzzy relations.
Results:
In this study, two scenarios are taken into considerations. In scenario-I, TFNs are used while in scenario-II, GFNs are taken to characterize uncertainty and medical decision making has been carried out. The advantages of GFNs over the TFNs are observed through the comparison of both the approaches in medical decision making. Major advantage GFNs here is that it makes it possible to compare various diseases against each other’s in a more acceptable manner and accordingly diseases of the patients can be detected directly.
Conclusion:
The advantage of the GFN approach has been observed from the case study where it is found that existing TFN approach provides illogical results while proposed one gives a rational result. Also, it has been established that proposed approach is efficient, simple, logical, technically sound and general enough for implementation.
Article Information
Identifiers and Pagination:
Year: 2018Volume: 12
First Page: 1
Last Page: 19
Publisher Id: TOCSJ-12-1
DOI: 10.2174/1874110X01812010001
Article History:
Received Date: 28/10/2017Revision Received Date: 28/12/2017
Acceptance Date: 30/01/2018
Electronic publication date: 22/02/2018
Collection year: 2018
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: (https://creativecommons.org/licenses/by/4.0/legalcode). This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
Correspondence: Address correspondence to this author at the Department of Mathematics, Dibrugarh University, Dibrugarh, Assam, India; Tel:+919435184995; E-mails: palash.dtt@gmail.com, palashdutta@dibru.ac.in
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 28-10-2017 |
Original Manuscript | Medical Decision Making via the Arithmetic of Generalized Triangular Fuzzy Numbers | |
1. INTRODUCTION
It has been observed that more often many real world representation models are soiled with vagueness/ ambiguity or uncertainty due to deficiency of precision, deficiency in data, diminutive sample sizes or data acquired from specialist opinion, artificial/manmade error, etc. To tackle such kind of uncertainty Zadeh [2L.A. Zadeh, "Fuzzy sets", Information and Control, vol. 8, pp. 338-353.
[http://dx.doi.org/10.1016/S0019-9958(65)90241-X] ] devised a hypothesis called as fuzzy set theory (FST). Afterward, plenty of supplementary direct or indirect extensions have been made by numerous canvassers. Chen [3S.H. Chen, "Operations on fuzzy numbers with function principal", Journal of Management Science, vol. 6, pp. 13-26.] further extended the conventional FST and developed generalized fuzzy numbers (GFN) where all the four arithmetic operations on GFNs were discussed using function principal. GFN can deal with uncertain data/information in a more bendy way in comparison to FST, as the height (w) that characterize the grade of buoyancy of judgments of decision takers in a very specific comportment.
Authors in [4S.H. Chen, and C.H. Hsieh, "Ranking generalized fuzzy number with graded mean integration representation", In: Proceedings of the eighth international conference of fuzzy sets and systems association world congress, vol. 2, pp. 551-555, 1999.] acknowledged that Chen’s arithmetic operations are altering the type of membership functions (MFs) together with diminishing the deficiency of arithmetic operations on GFNs. Nevertheless, it has been observed that Chen initially decreased the height of the GFN of bigger one to the height of the smaller one and then converted it into a new GFN and carried out all the four basic arithmetic operations; and as a result, it lost data/information and did not provide accurate output.
The key disadvantage of Chen’s method is to facilitate arithmetic operations between a fixed triangular GFN with dissimilar triangular GFNs with identical support but unusual heights where height of permanent GFN is smaller than the other GFNs then it is observed that every moment output triangular GFN is stay behind invariant which is really irrational. Dutta [5P. Dutta, "Comparison of Arithmetic Operations of Generalized Fuzzy Numbers: Case Study in Risk Assessment", Cybernetics and Systems, vol. 47, pp. 290-320.
[http://dx.doi.org/10.1080/01969722.2016.1182354] ] supplementary studied arithmetic operations between triangular GFNs and it is observed that this approach produces different trapezoidal type GFNs in the arithmetic of triangular GFNs and which is found to be more realistic.
1.1. Related Works
Zadeh [6L.A. Zadeh, "Biological Application of the theory of Fuzzy Sets and Systems", in Biocybernetics of the Central Nervous System, L . D. Proctor Ed. Little Brown: Boston, Mass, 1969, pp.199-212.] first applied FST in the field of medicine and Sanchez [7E. Sanchez, "Resolution of Composite Fuzzy Relation Equations", Information and Control, vol. 30, pp. 38-48.
[http://dx.doi.org/10.1016/S0019-9958(76)90446-0] , 8E. Sanchez, “Medical Diagnosis and Composite Fuzzy Relations”, in Advances in Fuzzy Set Theory and Applications, M.M. Gupta, R.K. Ragade, and R.R. Yager Eds. Amsterdam: North-Holland, 1979, pp. 437-444.] fully formulated the finding models relating to fuzzy matrices in lieu of the medical understanding between symptoms and diseases. Nowadays, medical diagnosis using fuzzy variables is much more popular among researchers. Decisions making for medical diagnosis based on fuzzy numbers along with compositional rule of inference were studied [9J.F. Yao, and J.S. Yao, "Fuzzy decision making for medical diagnosis based on fuzzy number and compositional rule of inference", Fuzzy Sets and Systems, vol. 120, pp. 351-366.
[http://dx.doi.org/10.1016/S0165-0114(99)00071-8] ]. Fuzzy set, rough set as well as soft set based medical analysis were discussed [10S.R. Dash, S. Dehuri, and U. Sahoo, "Usage of Fuzzy, Rough, and Soft Set Approach in Association Rule Mining", International Journal of Artificial Life Research (IJALR), vol. 3, pp. 64-77.
[http://dx.doi.org/10.4018/jalr.2012070105] ]. A procedure for medical diagnosis using fuzzy decision making was presented [11S. Elizabeth, and L. Sujatha, "Application of Fuzzy Membership Matrix in Medical Diagnosis and Decision Making", Applied Mathematical Sciences, vol. 7, pp. 6297-6307.]. A system for medical diagnosis was proposed that was generated using fuzzy logic toolbox in MATLAB [12P. Dagar, A. Jatain, and D. Gaur, "Medical diagnosis system using fuzzy logic toolbox", In: Computing, Communication & Automation
(ICCCA), 2015 International Conference on 2015 May 15, IEEE: India, 2015, pp. 193-197.
[http://dx.doi.org/10.1109/CCAA.2015.7148370] ]. Specifically, it focused on medical diagnosis. A fuzzy inference system created to support medical diagnoses in real time was presented [13I.B. De Medeiros, M.A. Machado, W.J. Damasceno, A.M. Caldeira, R.C. Dos Santos, and J.B. Da Silva Filho, "A Fuzzy Inference System to Support Medical Diagnosis in Real Time", Procedia Computer Science, vol. 122, pp. 167-173.
[http://dx.doi.org/10.1016/j.procs.2017.11.356] ]; the concept of weighted hesitant fuzzy set (WHFS) was redefined and subsequently applied in medical diagnosis [14B. Farhadinia, "A Hesitant Fuzzy Based Medical Diagnosis Problem", International Journal on Data Science and Technology, vol. 3, pp. 1-7.
[http://dx.doi.org/10.11648/j.ijdst.20170301.11] ].
Interval valued fuzzy soft set was also studied to exhibited the technique with hypothetical case study [15B. Chetia, and P.K. Das, "An application of Interval Valued Fuzzy Soft Set in Medical Diagnosis", International Journal of Contemporary Mathematical Sciences, vol. 5, pp. 1887-1894.]. A fuzzy diagnosis method based on the interval valued interview chart and the interval valued Intuitionistic fuzzy weighted arithmetic average operator was presented and studied the occurrence information symptoms as the weights [16J. Y. Ahn, K. S. Han, S. Y. Oh, and C. D. Lee, "An application of interval-valued intuitionistic fuzzy sets for medical diagnosis of headache", International Journal of Innovative Computing, Information and Control, vol. 7, pp. 2755-2762.]. Sanchez’s approach was extended for medical diagnosis using interval valued fuzzy matrix [17A.R. Meenakshi, and M. Kaliraja, "An application of interval valued fuzzy matrices in medical diagnosis", International Journal of Mathematical Analysis, vol. 5, pp. 1791-1802.], a fuzzy diagnosis method based on interval valued intuitonistic fuzzy sets (IVIFSs) was proposed in [18H.M. Choi, G.S. Mun, and J.Y. Ahn, "A medical diagnosis based on interval valued fuzzy set", Biomedical Engineering: Applications, Basis and Communications, vol. 24, pp. 349-354.]. Medical diagnosis based on IVFN matrices was also discussed [19S. Elizabeth, and L. Sujatha, "Medical Diagnosis Based on Interval Valued Fuzzy Number Matrices", Annals of Pure and Applied Mathematics, vol. 7, pp. 91-96.], also interval valued fuzzy sets was applied in medical diagnosis [1P. Dutta, "Decision Making in Medical Diagnosis via Distance Measures on Interval Valued Fuzzy Sets", International Journal of System Dynamics Applications, vol. 6, pp. 63-83.
[http://dx.doi.org/10.4018/IJSDA.2017100104] ].
De and coworkers [20S.K. De, R. Biswas, and A.R. Roy, "An application of intuitionistic fuzzy sets in medical diagnosis", Fuzzy Sets and Systems., vol. 117, pp. 209-213.
[http://dx.doi.org/10.1016/S0165-0114(98)00235-8] ] first deliberated medical diagnosis with the notion of IFS, medical diagnosis using distance measures was also studied [21E. Szmidt, and J. Kacprzyk, "Intuitionistic fuzzy sets in some medical applications", Lecture Notes in Computer Science, vol. 2206, pp. 148-151.
[http://dx.doi.org/10.1007/3-540-45493-4_19] ]. Advantages of type-2 fuzzy and switching relation between type-2 fuzzy sets were studied applied in medical diagnosis [22C.M. Own, "Switching between type-2 fuzzy sets and intuitionistic fuzzy sets: An application in medical diagnosis", Applied Intelligence, vol. 31, pp. 283-291.
[http://dx.doi.org/10.1007/s10489-008-0126-y] ]. Some other studies were made in medical diagnosis for IFSs [23A.E. Samuel, and M. Balamurugan, "Intuitionistic fuzzy set in medical diagnosis using ranking function", Surveys in Mathematics and Mathematical Science, vol. 2, pp. 23-34.-25A.E. Samuel, and M. Balamurugan, "Ifs with N-Parameters in Medical Diagnosis", International Journal of Pure and Applied Mathematics, vol. 84, pp. 185-192.
[http://dx.doi.org/10.12732/ijpam.v84i3.5] ]. Works of [20S.K. De, R. Biswas, and A.R. Roy, "An application of intuitionistic fuzzy sets in medical diagnosis", Fuzzy Sets and Systems., vol. 117, pp. 209-213.
[http://dx.doi.org/10.1016/S0165-0114(98)00235-8] ] was responded in [26K.C. Hung, and H.W. Tuan, "Medical diagnosis based on intuitionistic fuzzy sets revisited", Journal of Interdisciplinary Mathematics, vol. 16, pp. 385-395.
[http://dx.doi.org/10.1080/09720502.2013.841406] ]. An approach on divergence measures for IFSs was propsed and applied in medical diagnosis [27S. Maheshwari, and A. Srivastava, "Study on divergence measures for intuitonistic fuzzy sets and its application in medical diagnosis", Journal Of Applied Analysis And Computation, vol. 6, no. 3, pp. 772-789.]. Confirmation of the demand of IFSs in medical was studied [28B. B. Davvaz, and E.H. Sadrabadi, "An application of intuitionistic fuzzy sets in medicine", International Journal of Biomathematics, vol. 9, pp. 613-626.]. Decision support system in ICU via IFSs was also discussed [29H. Jemal, Z. Kechaou, and M. Ben Ayed, "Enhanced Decision Support Systems in Intensive Care Unit Based on Intuitionistic Fuzzy Sets", Advances in Fuzzy Systems, vol. 21, pp. 1-8.
[http://dx.doi.org/10.1155/2017/7371634] ], modal operator based on IFSs and its application in medical decision making was also done [30E. Samuel, and S. Rajakumar, "Intuitionistic Fuzzy Set with Modal Operators in Medical Diagnosis", Advances in Fuzzy Mathematics, vol. 12, pp. 167-176.].
Fuzzy soft set theory in medical diagnosis using fuzzy arithmetic operations was further studied [31Y. Çelik, and S. Yamak, "Fuzzy soft set theory applied to medical diagnosis using fuzzy arithmetic operations", Journal of Inequalities and Applications, vol. 2013, pp. 1-9.
[http://dx.doi.org/10.1186/1029-242X-2013-82] ]. The concept of bell-shaped fuzzy soft sets was first introduced and successfully applied in medical decision making [32P. Dutta, and B. Limboo, "Bell-shaped Fuzzy Soft Sets and Their Application in Medical Diagnosis", Fuzzy Information and Engineering, vol. 9, pp. 67-91.
[http://dx.doi.org/10.1016/j.fiae.2017.03.004] ]. Medical decision making using picture fuzzy set was also discussed [33P. Dutta, "Medical Diagnosis via Distance Measures on Picture Fuzzy", Advances in Modelling and Analysis, vol. 54, pp. 137-152.]. An improved hybrid approach for training the adaptive network based fuzzy inference system with Modified Levenberg-Marquardt algorithm using analytical derivation scheme for computation of Jacobian matrix was introduced [34A.M. Sagir, and S. Sathasivam, "Design of a modified adaptive neuro fuzzy inference system classifier for medical diagnosis of Pima Indians Diabetes", AIP Conference Proceedings, vol. 1870, p. 040048.
[http://dx.doi.org/10.1063/1.4995880] ].
1.2. Purpose of the Research
It is palpable that when individual(s) suffer from any types of diseases he/she/they often move toward to a medical expert while medical expert queries a patient about his/her state, then patients use the linguistic variable/expression to elucidate their states which are generally vague [1P. Dutta, "Decision Making in Medical Diagnosis via Distance Measures on Interval Valued Fuzzy Sets", International Journal of System Dynamics Applications, vol. 6, pp. 63-83.
[http://dx.doi.org/10.4018/IJSDA.2017100104] ]. Medical expert wants to assess a catalog of potential symptoms for the particular diseases of the patients based on their vague linguistic statements. Nevertheless, the associations between symptoms and diseases are not often one-to-one. The exposition of the identical disease may not be equal with dissimilar patients and even at dissimilar disease stages. Furthermore, it should be noted that a meticulous symptom can point out diverse diseases and in a number of circumstances in a meticulous patient may dismay the presumed formation of symptoms. On the other hand, knowledge base correlating the symptom-disease relationship comprises of ambiguity, imprecision, vagueness and uncertainty in medical decision making process. Most frequently, type-I fuzzy set, IFS, IVFSs, PFSs are employed for medical decision making purpose, but some situations it leads to counter intuitive results. Hence, GFNs can be employed as the representation of the state and symptoms of the patient that can be only known by medical experts with a very partial grade of precision. Therefore, triangular GFNs have been taken in this study as the GFN has the skill to deal with vague data/information in a more stretchy way because of the parameter height that characterize the degree of confidence of opinions of decision maker’s as the height of GFN characterize the grade of buoyancy of judgments of decision takers in a very specific comportment. Thus, it can be opined that GFN has more importance in medical decision making process and can effectively be used.
1.3. Contributions
The applicability and legalization of the study has been shown by solving medical decision making problems via two ways. The current study made it feasible to instigate weights of all signs of diseases correctly and in view of that patients can be diagnosed straightforwardly. It is monitored that it confers efficient, flexible, simple, logical, technically sound solution for medical decision making problem. It is also attained that the GFNs have paramount significant role in medical decision making problem. The advantages of this study can be pointed out as follows: it offers an effort to carry out medical diagnosis by considering medical expert’s medical knowledge in terms of GFNs; it has more usefulness because of its capability to address imprecision/vagueness/uncertainty in a proper manner; it also offers assistance to medical experts to carry out medical diagnosis providing better efficiency to the output and people living in the rural areas will be mostly benefited.
1.4. Objectives
In this paper, a maiden effort has been made to bring out medical diagnosis using GTFN via the approach [5P. Dutta, "Comparison of Arithmetic Operations of Generalized Fuzzy Numbers: Case Study in Risk Assessment", Cybernetics and Systems, vol. 47, pp. 290-320.
[http://dx.doi.org/10.1080/01969722.2016.1182354] ].
2. PRELIMINARIES
Let X be a universe of discourse. Then the fuzzy subset A of X is defined by its membership function
 |
Which allocate a real number  in the interval [0, 1], to each element
in the interval [0, 1], to each element , wherever the value of
, wherever the value of  show the grade of membership of x in A.
show the grade of membership of x in A.
2.1. Generalized Fuzzy Numbers (GFN)
The membership function of GFN A= [a,b,c,d;w] where a ≤ b ≤ c ≤ d , 0 < w ≤ 1 is defined as
 |
If  , then the GFN A is called a trapezoidal GFN. If
, then the GFN A is called a trapezoidal GFN. If  , then GFN A is a normal trapezoidal fuzzy number [ a, b, c, d ]. If a = b and c = d, then A is a crisp interval .If b = c then A is a triangular GFN. If a = b = c and w = 1 then A is a real number.
, then GFN A is a normal trapezoidal fuzzy number [ a, b, c, d ]. If a = b and c = d, then A is a crisp interval .If b = c then A is a triangular GFN. If a = b = c and w = 1 then A is a real number.
3. ARITHMETIC OPERATIONS ON GTFNs
Let A and B be two triangular GFNs with heights  respectively whose MFs are given
respectively whose MFs are given
 |
The α α-cuts of the triangular GFNs A and B are
 |
respectively.
3.1. Theorem: Addition of Triangular GFNs Produces a Trapezoidal GFN
Proof: To evaluate addition of triangular GFNs A and B, it is needed to sum the α-cut of the triangular GFNs A and B using the method of arithmetic of intervals.
 |
 |
(1) |
To gauge the output  we need to equate both the first and second component of (1) to x that provides
we need to equate both the first and second component of (1) to x that provides
 |
Then, express α in terms of x and putting α ≥ 0 and α ≤ w in (1) we obtain α together with the domain of x,
 |
that produces
 |
This is obviously a trapezoidal GFN with height w at
 |
Hence proved the theorem
3.2. Theorem: Subtraction of Triangular GFNs Produces a Trapezoidal GFN
Proof: Here also, to evaluate subtraction of triangular GFNs A and B, it is needed to subtract the α-cuts of A and B using the method of interval arithmetic.
 |
(2) |
where  and
and  .
.
To evaluate the output  we need to equate both the first and second component of (2) to x which gives
we need to equate both the first and second component of (2) to x which gives
 |
Then, express α in terms of x and putting α ≥ 0 and α ≤ w in (2) we have α together with the domain of x
 |
The MF of the resulting GFN after subtraction of A and B is obtained as
 |
where  and
and  .
.
Similarly, this is also a MF of the output trapezoidal GFN with height w at
 |
Hence proved the theorem
3.3. Theorem: Product of Triangular GFNs Produces a Trapezoidal Type GFN
Proof: To evaluate product of triangular GFNs A and B, we need to initially product the αα-cuts of A and B using the approach of interval arithmetic.
 |
(3) |
where  and
and 
To obtain the required  we need to equate both the first and second component of (3) to x which gives:
we need to equate both the first and second component of (3) to x which gives:
 |
this is a quadratic equation and solving we obtain
 |
Similarly
 |
 |
Now, setting α ≥ 0 and α ≤ w in (3) we get the required MF of the resulting GFN after multiplication of A and B simultaneously with the domain of x
 |
This is obviously a MF of trapezoidal type GFN with height w at
 |
Hence proved the theorem
3.4. Theorem: Division of Triangular GFNs Produces a Trapezoidal Type GFN
Proof: To divide triangular GFNs A and B, it is needed to divide the α-cut of A and B using the method of interval arithmetic.
 |
(4) |
where  and
and  .
.
To evaluate the  we need to equate both the first and second component of (4) to x, which gives
we need to equate both the first and second component of (4) to x, which gives
 |
Then, expressing α in terms of x and then setting α ≥ 0 and α ≤ w in (4) we obtain α together with the domain of x
 |
 |
The MF of the output trapezoidal GFN is obtained as
 |
Obviously this is a MF of a trapezoidal type GFN with height w at
 |
Hence proved the theorem
4. A NORMALIZED APPROACH
To conquer the difficulty of computation (arithmetic operation), Dutta [5P. Dutta, "Comparison of Arithmetic Operations of Generalized Fuzzy Numbers: Case Study in Risk Assessment", Cybernetics and Systems, vol. 47, pp. 290-320.
[http://dx.doi.org/10.1080/01969722.2016.1182354] ] adopted traditional computational loom (α-cut technique). For which first normalized the specified GFNs and carry out (computations) arithmetic operations. Then the consequential fuzzy number obtained is a normal fuzzy number. To get resulting GFN, truncated the resulting normal fuzzy number at the least height of the given GFNs [5P. Dutta, "Comparison of Arithmetic Operations of Generalized Fuzzy Numbers: Case Study in Risk Assessment", Cybernetics and Systems, vol. 47, pp. 290-320.
[http://dx.doi.org/10.1080/01969722.2016.1182354] ].
For example, suppose A=[a1,b1,c1;w1] and B=[a2,b2,c2;w2] are triangular GFNs. To carry out arithmetic between A and B, first simplified both the GFNs and then execute arithmetic operations between the normalized fuzzy numbers [5P. Dutta, "Comparison of Arithmetic Operations of Generalized Fuzzy Numbers: Case Study in Risk Assessment", Cybernetics and Systems, vol. 47, pp. 290-320.
[http://dx.doi.org/10.1080/01969722.2016.1182354] ]. P=[p,q,r], is the output fuzzy number. To obtain exact output trapezoidal GFN [5P. Dutta, "Comparison of Arithmetic Operations of Generalized Fuzzy Numbers: Case Study in Risk Assessment", Cybernetics and Systems, vol. 47, pp. 290-320.
[http://dx.doi.org/10.1080/01969722.2016.1182354] ], truncated the normal fuzzy number P at w=min (w1,w2). After that the MFs of the output trapezoidal GFNs are obtained as follows:
 |
 |
 |
 |
5. NUMERICAL EXAMPLES
Let A and B be triangular GFNs whose MF are given as
 |
To evaluate the MFs of the trapezoidal GFNs A+B using approach [5P. Dutta, "Comparison of Arithmetic Operations of Generalized Fuzzy Numbers: Case Study in Risk Assessment", Cybernetics and Systems, vol. 47, pp. 290-320.
[http://dx.doi.org/10.1080/01969722.2016.1182354] ], we first sum up α-cut of the triangular GFNs A and B.
 |
respectively.
Now,
 |
 |
(5) |
Equating both the first and second component of (5) to x and expressing α in terms of x, we have
 |
Putting α ≥ 0 and α ≤ 0.7 in (5) we obtain α together with the domain of x,
 |
Thus the resultant MF of the trapezoidal GFN is
 |
On the other hand, to employ normalized approach, first we normalize the triangular GFN A and B by dividing the MFs by 0.8 and 0.7 respectively and which are
 |
Using approach [35P. Dutta, H. Boruah, and T. Ali, "Fuzzy arithmetic with and without using α-cut method: a comparative study", International Journal of Latest Trends in Computing, vol. 2, pp. 99-108.] of arithmetic of normal fuzzy numbers, we have the following resultant normal fuzzy number
 |
Discretizing the fuzzy number at minimum height 0.7, we have
 |
Similarly, the other consequential trapezoidal GFNs can be evaluated using approach [5P. Dutta, "Comparison of Arithmetic Operations of Generalized Fuzzy Numbers: Case Study in Risk Assessment", Cybernetics and Systems, vol. 47, pp. 290-320.
[http://dx.doi.org/10.1080/01969722.2016.1182354] ] and normalized approach which are respectively given in the following Table (1).

Resulting GFNs obtained using approach [5P. Dutta, "Comparison of Arithmetic Operations of Generalized Fuzzy Numbers: Case Study in Risk Assessment", Cybernetics and Systems, vol. 47, pp. 290-320.
[http://dx.doi.org/10.1080/01969722.2016.1182354] ] and Normalized Approach.
6. RANKING OF TRAPEZOIDAL GFNs
Let A = [ a, b, c, d; w ] be a trapezoidal GFN and  be the α α-cut of A. After that the value of A can be defined as:
be the α α-cut of A. After that the value of A can be defined as:
 |
Where  is a non-negative and non-decreasing function on
is a non-negative and non-decreasing function on  and
and  .
.
Here, we also choose  .
.
Thus, the value of the trapezoidal GFN A is evaluated as:
 |
(6) |
7. METHODOLOGY
As medical documents, information even medical decision making process fouled with vagueness/imprecision/uncertainty. Again, knowledge base correlating the symptom-disease relationship comprises of ambiguity, imprecision, vagueness and uncertainty in medical decision making process. Consequently fuzzy set theory became popular aid in medical decision making process. Generally, type-I fuzzy set, IFSs, IVFSs and PFSs are used for medical decision making. However, these tools provide counterintuitive results. For example,
De and colleagues first deliberated medical diagnosis with the notion of IFS [20S.K. De, R. Biswas, and A.R. Roy, "An application of intuitionistic fuzzy sets in medical diagnosis", Fuzzy Sets and Systems., vol. 117, pp. 209-213.
[http://dx.doi.org/10.1016/S0165-0114(98)00235-8] ]. Then, a further study in medical diagnosis has been done using the same IFS medical data and criticized the earlier study having with different results [21E. Szmidt, and J. Kacprzyk, "Intuitionistic fuzzy sets in some medical applications", Lecture Notes in Computer Science, vol. 2206, pp. 148-151.
[http://dx.doi.org/10.1007/3-540-45493-4_19] ]. Numerous studies have been made on medical diagnosis problem for the same IFSs data and obtained different results from the existing studies ([22C.M. Own, "Switching between type-2 fuzzy sets and intuitionistic fuzzy sets: An application in medical diagnosis", Applied Intelligence, vol. 31, pp. 283-291.
[http://dx.doi.org/10.1007/s10489-008-0126-y] ], [36I.K. Vlachos, and G.D. Sergiadis, "Intuitionistic fuzzy information–applications to pattern recognition", Pattern Recognition Letters, vol. 28, pp. 197-206.
[http://dx.doi.org/10.1016/j.patrec.2006.07.004] -39Y. Song, X. Wang, and L. Lei, "A novel similarity measure on intuitionistic fuzzy sets with its applications", Applied Intelligence, vol. 42, pp. 252-261.
[http://dx.doi.org/10.1007/s10489-014-0596-z] ]). Later, a comparative study has been made via the existing distance measures for the same medical diagnosis problem and obtained different results except with the second study in this sequence [28B. B. Davvaz, and E.H. Sadrabadi, "An application of intuitionistic fuzzy sets in medicine", International Journal of Biomathematics, vol. 9, pp. 613-626.]. It is seen that for the same diagnosis problem addressed by various researchers using different approaches lead to different chaotic results. Similar types of counter intuitive results also occur for other uncertainty modeling tools.
Therefore, GFNs can be employed as the representation of the state and symptoms of the patient that can be only known by medical experts with a very partial grade of precision. Therefore, triangular GFNs have been taken in this study as the GFN has the skill to deal with vague data/information in a more stretchy way because of the parameter height that characterize the degree of confidence of opinions of decision maker’s in a very specific deportment. Advantages of GFNs over the normal fuzzy numbers have been demonstrated in the case study section.
The methodology for medical decision making can be summarized as suppose P, S and D are the sets of patients, symptoms and diseases respectively. To identify the patients and their corresponding disease that they are suffering from, it is utmost important to determine the symptoms and accordingly need to formulate the medical knowledge via fuzzy relations say, symptoms-diseases (Q) and patient-symptoms fuzzy (R) with the help of doctors/experts/physicians.
To gauge the patients-diseases relation (T) the following composition can be adopted
 |
(7) |
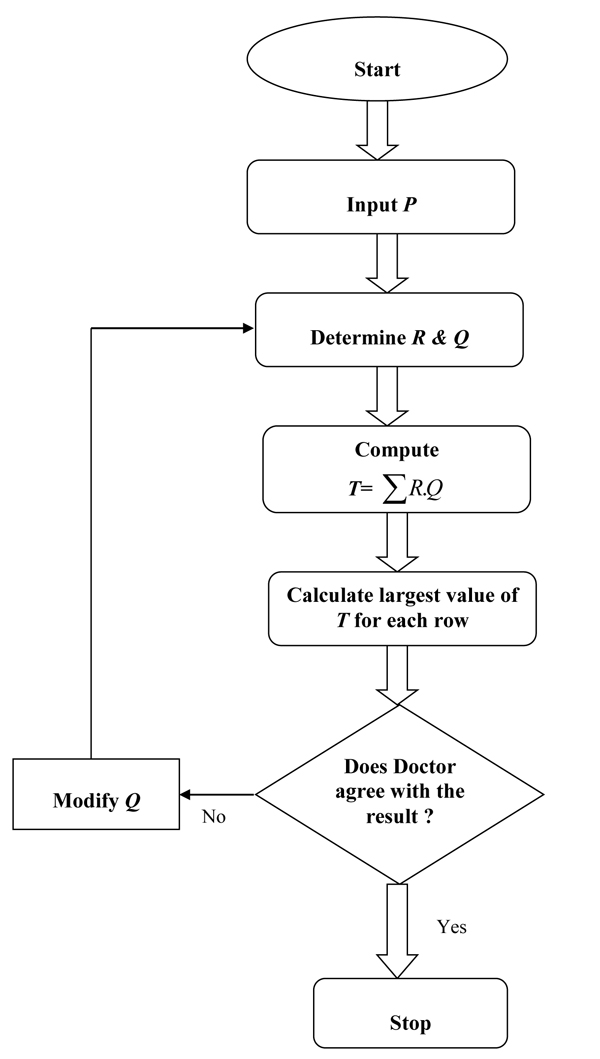
The entries of the patients-diseases relation (T) will be Trapezoidal GFNs. Then, ranking of the Trapezoidal GFNs can be computed using value. It should be noted that the maximum value in each row indicate that the patient is likely to have the disease. If doctor/expert/physician does not satisfy with the result, then modification will be done on symptoms-diseases (Q) and compute from the beginning. A flowchart has been depicted in Fig. (1 ) in appendix section for easy understanding of the readers.
) in appendix section for easy understanding of the readers.
7.1. Case Study
In this segment, a hypothetic case study for medical decision making has been carried out using arithmetic of triangular GFNs via value.
Suppose Pranjal, Rupjit,and Soumendra are admitted in Assam Medical College hospital at Dibruagrh, India. The symptoms of the patients are found to be temperature, headache, cough and stomach pain. The diseases for these symptoms found by doctor/expert/physician are Viral Fever, Typhoid and Malaria. Require to identify which patient is exactly suffering from which disease.
To perform medical diagnosis Mathematically, let P = {Pranjal, Rupjit, Soumendra}, be the set of patients; S = {temperature, headache, cough, stomach pain} be the set of symptoms and D = {Viral Fever, Typhoid, Malaria} be the set of diseases respectively.
7.1.1. Scenario-I
The medical knowledge via fuzzy relations say, symptoms-diseases (Q) and patient-symptoms fuzzy (R) have been compiled from Çelik and Yamakand (2013) and respectively depicted in Tables (2 and 3). Here, heights of all the fuzzy numbers are considered equal to unit (i.e., w=1).
Using the proposed composition of fuzzy relation (7), the following patients-diseases relation Table (4) is obtained.
As all entries here are triangular fuzzy numbers with w=1
Thus, the value of the triangular fuzzy number A = [a,b,c] will be
 |
(8) |
Using equation (8) we have the following resultant value of each entries of patients-diseases relation Table (5).
The maximum value in each row indicates that the patient is likely to have the disease. Thus, we can conclude that Pranjal is suffering from viral fever while Rupjit and Soumendr both are suffering from Typhoid. But, proper analysis of the medical data set it could be found that Rupjit suffers from viral fever. Since for the patient Rupjit the maximum value among the symptoms occurs for temperature while for the symptom temperature the maximum value among the diseases occurs for viral fever and hence it general intuition that Rupjit is suffering from viral fever. However, analytical data corroborates the same fact about patients Pranjal and Soumendra.
7.1.2. Scenario-2
It is observed that due to consideration of heights of fuzzy numbers lead to illogical results. Therefore, here details relationships between symptoms and diseases are studies and accordingly degree of relationships have been assigned in terms of Triangular GFNs.
A viral fever is characterized by a very high fever that is often remittent where the fever abates for a little while and then shoots up once again. Hence, temperature is much more than 104oF. On the other hand, for typhoid temperature is more than 104oF. Again, for malariatemperature is high i.e., it lies between 103oF-104oF. Thus, keeping all these in mind, the degree of relationships (temperature, viral fever), (temperature, typhoid) and (temperature, malaria) have been precisely assigned in a very specific comportment in terms of triangular GFNs. It is also well known that headache is a common symptom for the three diseases and in a similar fashion degree of relationships of headache with the diseases have been assigned. Cough is a major symptom of viral fever while it has less relationship with typhoid and malaria. The symptom stomach pain has less relationship with the diseases under study.
A detail the data set regarding symptoms-diseases (Q) and patient-symptoms fuzzy (R) have been depicted in Table (6 and 7).
Using the composition of relations (7), patient-disease relation (T) is evaluated and depicted in Table (8).
Then, each entry of the patient-disease relation (T) is defuzzified using value and is given in Table (9). It should be noted that maximum value in each row indicates that the patient is likely to have the disease.
8. RESULTS AND DISCUSSIONS
Normally, a disease is pigeonholed by symptoms which encourage the patient to approach to a medical expert. A collection of experimental assessments are commenced to recognize the happening of a disease. In the area of medical decision making, plenty of variables are there which persuade the decision making process and accordingly, distinguish the opinions of the doctors/physicians. Due to so many factors to analyze for the finding of the disease of a patient makes the medical expert’s job complicated.
As most of the medical decision making setback involves dealing with vagueness and uncertainties and it is needed to contain of all the information into investigation. In the case study, two scenarios are taken into considerations. In scenario-I, TFNs are used to characterize uncertainty and medical decision making has been carried out in this study. To organize the data base, for the patients Pranjal Rupjit and Soumendra; four symptoms Temperature, Headache, Cough and Stomachpain and three diseases, Viral Fever, Typhoid and Malaria are considered. Finally, patients-diseases relation has been computed. It is found that Pranjal suffers from viral fever while Rupjit and Soumendra both are suffering from Typhoid. But, which is irrational for the patient Rupjit. That is, it is clear from the data set that Rupjit is suffering from viral fever but the approach gives that it is typhoid. Therefore, in scenario-II, triangular GFNs are assigning instead of TFNs to characterize uncertainty and medical decision making has been performed here using proposed arithmetic on GFNs as composition of relation and finally values have been evaluated using equation (2). It is found that Pranjal and Rupjit are suffering from viral fever while Soumendra is suffers from typhoid which is more realistic.
CONCLUSION
GFN, a direct generalization of FST, has received more and more attention in the field of decision making, science and technology, risk assessment, etc. because of the height of GFN to characterize the grade of buoyancy of judgments of decision takers in a very specific comportment. In this editorial the concept of arithmetic on triangular GFN proposed by Dutta [5P. Dutta, "Comparison of Arithmetic Operations of Generalized Fuzzy Numbers: Case Study in Risk Assessment", Cybernetics and Systems, vol. 47, pp. 290-320.
[http://dx.doi.org/10.1080/01969722.2016.1182354] ] has been reviewed which can successfully covenant with vagueness, imprecision, uncertainty with vagueness, imprecision, uncertainty and also applied in medical decision making for first time. For this purpose, this document presents an appropriate algorithm to perform medical decision making in which arithmetic on triangular GFNs have been used as composition of fuzzy relations. A case study has been performed via two scenarios. The advantage of the proposed approach has been observed from the cast study where it is found that existing approach provides illogical results while proposed one gives a rational result. Hence, it is established that proposed approach is efficient, simple, logical, technically sound and general enough for implementation not only in medical decision making but also in other allied fields.
In some situations, existence of different types of uncertainties leads to imprecise fuzzy set membership functions and as a consequence ordinary FST is inappropriate to model such types of uncertainties. IVFS and type-II fuzzy sets are capable of modeling uncertainties, therefore as an extension of this editorial generalized IVFSs and type-II fuzzy sets will be studied along with attempt will be made to employ in medical investigations.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
This research was supported by the Natural Science Foundation of China (No. 71272209).
REFERENCES
| [1] | P. Dutta, "Decision Making in Medical Diagnosis via Distance Measures on Interval Valued Fuzzy Sets", International Journal of System Dynamics Applications, vol. 6, pp. 63-83. [http://dx.doi.org/10.4018/IJSDA.2017100104] |
| [2] | L.A. Zadeh, "Fuzzy sets", Information and Control, vol. 8, pp. 338-353. [http://dx.doi.org/10.1016/S0019-9958(65)90241-X] |
| [3] | S.H. Chen, "Operations on fuzzy numbers with function principal", Journal of Management Science, vol. 6, pp. 13-26. |
| [4] | S.H. Chen, and C.H. Hsieh, "Ranking generalized fuzzy number with graded mean integration representation", In: Proceedings of the eighth international conference of fuzzy sets and systems association world congress, vol. 2, pp. 551-555, 1999. |
| [5] | P. Dutta, "Comparison of Arithmetic Operations of Generalized Fuzzy Numbers: Case Study in Risk Assessment", Cybernetics and Systems, vol. 47, pp. 290-320. [http://dx.doi.org/10.1080/01969722.2016.1182354] |
| [6] | L.A. Zadeh, "Biological Application of the theory of Fuzzy Sets and Systems", in Biocybernetics of the Central Nervous System, L . D. Proctor Ed. Little Brown: Boston, Mass, 1969, pp.199-212. |
| [7] | E. Sanchez, "Resolution of Composite Fuzzy Relation Equations", Information and Control, vol. 30, pp. 38-48. [http://dx.doi.org/10.1016/S0019-9958(76)90446-0] |
| [8] | E. Sanchez, “Medical Diagnosis and Composite Fuzzy Relations”, in Advances in Fuzzy Set Theory and Applications, M.M. Gupta, R.K. Ragade, and R.R. Yager Eds. Amsterdam: North-Holland, 1979, pp. 437-444. |
| [9] | J.F. Yao, and J.S. Yao, "Fuzzy decision making for medical diagnosis based on fuzzy number and compositional rule of inference", Fuzzy Sets and Systems, vol. 120, pp. 351-366. [http://dx.doi.org/10.1016/S0165-0114(99)00071-8] |
| [10] | S.R. Dash, S. Dehuri, and U. Sahoo, "Usage of Fuzzy, Rough, and Soft Set Approach in Association Rule Mining", International Journal of Artificial Life Research (IJALR), vol. 3, pp. 64-77. [http://dx.doi.org/10.4018/jalr.2012070105] |
| [11] | S. Elizabeth, and L. Sujatha, "Application of Fuzzy Membership Matrix in Medical Diagnosis and Decision Making", Applied Mathematical Sciences, vol. 7, pp. 6297-6307. |
| [12] | P. Dagar, A. Jatain, and D. Gaur, "Medical diagnosis system using fuzzy logic toolbox", In: Computing, Communication & Automation
(ICCCA), 2015 International Conference on 2015 May 15, IEEE: India, 2015, pp. 193-197. [http://dx.doi.org/10.1109/CCAA.2015.7148370] |
| [13] | I.B. De Medeiros, M.A. Machado, W.J. Damasceno, A.M. Caldeira, R.C. Dos Santos, and J.B. Da Silva Filho, "A Fuzzy Inference System to Support Medical Diagnosis in Real Time", Procedia Computer Science, vol. 122, pp. 167-173. [http://dx.doi.org/10.1016/j.procs.2017.11.356] |
| [14] | B. Farhadinia, "A Hesitant Fuzzy Based Medical Diagnosis Problem", International Journal on Data Science and Technology, vol. 3, pp. 1-7. [http://dx.doi.org/10.11648/j.ijdst.20170301.11] |
| [15] | B. Chetia, and P.K. Das, "An application of Interval Valued Fuzzy Soft Set in Medical Diagnosis", International Journal of Contemporary Mathematical Sciences, vol. 5, pp. 1887-1894. |
| [16] | J. Y. Ahn, K. S. Han, S. Y. Oh, and C. D. Lee, "An application of interval-valued intuitionistic fuzzy sets for medical diagnosis of headache", International Journal of Innovative Computing, Information and Control, vol. 7, pp. 2755-2762. |
| [17] | A.R. Meenakshi, and M. Kaliraja, "An application of interval valued fuzzy matrices in medical diagnosis", International Journal of Mathematical Analysis, vol. 5, pp. 1791-1802. |
| [18] | H.M. Choi, G.S. Mun, and J.Y. Ahn, "A medical diagnosis based on interval valued fuzzy set", Biomedical Engineering: Applications, Basis and Communications, vol. 24, pp. 349-354. |
| [19] | S. Elizabeth, and L. Sujatha, "Medical Diagnosis Based on Interval Valued Fuzzy Number Matrices", Annals of Pure and Applied Mathematics, vol. 7, pp. 91-96. |
| [20] | S.K. De, R. Biswas, and A.R. Roy, "An application of intuitionistic fuzzy sets in medical diagnosis", Fuzzy Sets and Systems., vol. 117, pp. 209-213. [http://dx.doi.org/10.1016/S0165-0114(98)00235-8] |
| [21] | E. Szmidt, and J. Kacprzyk, "Intuitionistic fuzzy sets in some medical applications", Lecture Notes in Computer Science, vol. 2206, pp. 148-151. [http://dx.doi.org/10.1007/3-540-45493-4_19] |
| [22] | C.M. Own, "Switching between type-2 fuzzy sets and intuitionistic fuzzy sets: An application in medical diagnosis", Applied Intelligence, vol. 31, pp. 283-291. [http://dx.doi.org/10.1007/s10489-008-0126-y] |
| [23] | A.E. Samuel, and M. Balamurugan, "Intuitionistic fuzzy set in medical diagnosis using ranking function", Surveys in Mathematics and Mathematical Science, vol. 2, pp. 23-34. |
| [24] | A.E. Samuel, and M. Balamurugan, "Intuitionistic fuzzy set with rank correlation technique in medical diagnosis", Proceedings of the International Conference on Mathematics in Engineering & Business Management, Stella Maris College: Chennai, Tamil Nadu, India, . |
| [25] | A.E. Samuel, and M. Balamurugan, "Ifs with N-Parameters in Medical Diagnosis", International Journal of Pure and Applied Mathematics, vol. 84, pp. 185-192. [http://dx.doi.org/10.12732/ijpam.v84i3.5] |
| [26] | K.C. Hung, and H.W. Tuan, "Medical diagnosis based on intuitionistic fuzzy sets revisited", Journal of Interdisciplinary Mathematics, vol. 16, pp. 385-395. [http://dx.doi.org/10.1080/09720502.2013.841406] |
| [27] | S. Maheshwari, and A. Srivastava, "Study on divergence measures for intuitonistic fuzzy sets and its application in medical diagnosis", Journal Of Applied Analysis And Computation, vol. 6, no. 3, pp. 772-789. |
| [28] | B. B. Davvaz, and E.H. Sadrabadi, "An application of intuitionistic fuzzy sets in medicine", International Journal of Biomathematics, vol. 9, pp. 613-626. |
| [29] | H. Jemal, Z. Kechaou, and M. Ben Ayed, "Enhanced Decision Support Systems in Intensive Care Unit Based on Intuitionistic Fuzzy Sets", Advances in Fuzzy Systems, vol. 21, pp. 1-8. [http://dx.doi.org/10.1155/2017/7371634] |
| [30] | E. Samuel, and S. Rajakumar, "Intuitionistic Fuzzy Set with Modal Operators in Medical Diagnosis", Advances in Fuzzy Mathematics, vol. 12, pp. 167-176. |
| [31] | Y. Çelik, and S. Yamak, "Fuzzy soft set theory applied to medical diagnosis using fuzzy arithmetic operations", Journal of Inequalities and Applications, vol. 2013, pp. 1-9. [http://dx.doi.org/10.1186/1029-242X-2013-82] |
| [32] | P. Dutta, and B. Limboo, "Bell-shaped Fuzzy Soft Sets and Their Application in Medical Diagnosis", Fuzzy Information and Engineering, vol. 9, pp. 67-91. [http://dx.doi.org/10.1016/j.fiae.2017.03.004] |
| [33] | P. Dutta, "Medical Diagnosis via Distance Measures on Picture Fuzzy", Advances in Modelling and Analysis, vol. 54, pp. 137-152. |
| [34] | A.M. Sagir, and S. Sathasivam, "Design of a modified adaptive neuro fuzzy inference system classifier for medical diagnosis of Pima Indians Diabetes", AIP Conference Proceedings, vol. 1870, p. 040048. [http://dx.doi.org/10.1063/1.4995880] |
| [35] | P. Dutta, H. Boruah, and T. Ali, "Fuzzy arithmetic with and without using α-cut method: a comparative study", International Journal of Latest Trends in Computing, vol. 2, pp. 99-108. |
| [36] | I.K. Vlachos, and G.D. Sergiadis, "Intuitionistic fuzzy information–applications to pattern recognition", Pattern Recognition Letters, vol. 28, pp. 197-206. [http://dx.doi.org/10.1016/j.patrec.2006.07.004] |
| [37] | J. Ye, "Cosine similarity measures for intuitionistic fuzzy sets and their applications", Mathematical and Computer Modelling, vol. 53, pp. 1-7. [http://dx.doi.org/10.1016/j.mcm.2010.07.022] [PMID: 21076663] |
| [38] | F.E. Boran, and D. Akay, "A biparametric similarity measure on intuitionistic fuzzy sets with applications to pattern recognition", Information Sciences, vol. 255, pp. 45-57. [http://dx.doi.org/10.1016/j.ins.2013.08.013] |
| [39] | Y. Song, X. Wang, and L. Lei, "A novel similarity measure on intuitionistic fuzzy sets with its applications", Applied Intelligence, vol. 42, pp. 252-261. [http://dx.doi.org/10.1007/s10489-014-0596-z] |