The Open Cybernetics & Systemics Journal




(Discontinued)

ISSN: 1874-110X ― Volume 12, 2018
RESEARCH ARTICLE

Fuzzy Decision Making in Medical Diagnosis Using an Advanced Distance Measure on Intuitionistic Fuzzy Sets



Palash Dutta*, Soumendra Goala
Department of Mathematics, Dibrugarh University, Dibrugarh, Assam, India

Abstract

Background:

Decision making in medical diagnosis is becoming a vast research field in medical science. In the last few decades, the role of distance measure in decision science is significant. Various distance measures on IFSs have been developed by many researchers and used in medical diagnosis in last few decades.

Objective:

Medical diagnosis is one of the major decision-making situation in medical science. From the existing research and knowledge in medical science, the major, as well as minor symptoms of almost all disease, are recorded. In the initial stage of any disease, the symptoms of the patients are observed carefully and comparing the symptoms one can suggest the disease may be suffered by the patient. Therefore, an attempt has been made to practice a fuzzy decision-making approach using intuitionistic fuzzy sets. In addition, a novel distance measure on IFSs has been introduced.

Uncertainty in Medical Diagnosis:

Uncertainty is a factor which makes the decision-making process more difficult in medical diagnosis. Everyone is different from the other at physical level as well as mental level, symptoms of a disease expressed by patients are linguistic in nature and vary person to person. For example, the pain suffered in stomach by a patient usually expressed in linguistic expressions such as much, too much, severe etc. From the described symptoms by patients, a physician decides possible disease suffered by the patients. For this reason, in medical diagnosis, decision-making under uncertainty arises.

Result:

In this paper, a new distance measure between two Intuitionistic Fuzzy Sets (IFSs) has been proposed. The proposed distance measure has been used in a decision-making problem of a medical diagnosis problem. In addition, the result has been analyzed by comparing with the existing result of medical diagnosis.

Conclusion:

The result obtained by the case study carried out with the help of the proposed distance measure is analyzed by comparing results with the existing result of medical diagnosis. This is found to be very much similar to the existing result of medical diagnosis. This concludes the efficiency and reliability of our proposed distance measure.

Keywords: Intuitionistic fuzzy Set, Decision making, Distance measure, Medical diagnosis, Fuzzy optimization.

Article Information


Identifiers and Pagination:

Year: 2018
Volume: 12
First Page: 136
Last Page: 149
Publisher Id: TOCSJ-12-136
DOI: 10.2174/1874110X01812010136

Article History:

Received Date: 20/6/2018
Revision Received Date: 8/8/2018
Acceptance Date: 15/8/2018
Electronic publication date: 23/10/2018
Collection year: 2018

© 2018 Dutta and Goala.

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: (https://creativecommons.org/licenses/by/4.0/legalcode). This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.


* Address correspondence to this author at the Department of Mathematics, Dibrugarh University, Dibrugarh, Assam, India; Tel: +919435184995; E-mail: palash.dtt@gmail.com



1. INTRODUCTION

Initially, Zadeh in 1965, introduced the concept of Fuzzy Set Theory (FST) [1L.A. Zadeh, "Fuzzy sets", Inf. Control, vol. 8, pp. 338-353.
[http://dx.doi.org/10.1016/S0019-9958(65)90241-X] ]. Later, in 1986, Atanassov developed the system of IFS [2K.T. Atanassov, "Intuitionistic fuzzy sets", Fuzzy Sets Syst., vol. 20, pp. 87-96.
[http://dx.doi.org/10.1016/S0165-0114(86)80034-3] ] as an extension of classic fuzzy set theory. In fuzzy set theory, an element in the universal set is assigned to a membership degree. But, in IFSs theory, an element in the universal set is assigned to each element a membership degree, a non-membership degree and a hesitation degree. This is one of the main reason why IFS has been treated as a more effective and efficient concept than the FST to deal with the uncertainty in decision making. In recent years, significant effort has been made by researchers to show efficiency of IFS in the uncertainty modelling problems and applicability in a wide range of areas, such as decision making, fuzzy optimization, pattern recognition, medical diagnosis etc.

The similarity measure is important tools that can be used in decision-making problem to deal with uncertainty through IFS theory. Various distance measures have been proposed by different researchers. It has been observed that different distance measure produces different values while measuring the distance degree between two IFSs. Also, sometimes existing distance measures are not able to give an appropriate and convenient result for a pair of IFSs. For this reason, it is always necessary to derive advanced measures for better decision making.

Several similarity measures have been introduced on IFS by many researchers. Li et al. in 2002 [3D.F. Li, and C.T. Cheng, "New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions", Pattern Recognit. Lett., vol. 23, pp. 221-225.
[http://dx.doi.org/10.1016/S0167-8655(01)00110-6] ], Liang et al. in 2003 [4Z.Z. Liang, and P.F. Shi, "Similarity measures on intuitionistic fuzzy sets", Pattern Recognit. Lett., vol. 24, pp. 2687-2693.
[http://dx.doi.org/10.1016/S0167-8655(03)00111-9] ], Li et al. 2007 [5Y. Li, D.L. Olson, and Z. Qin, "Similarity measures between intuitionistic fuzzy (vague) sets: A comparative analysis", Pattern Recognit. Lett., vol. 28, pp. 278-285.
[http://dx.doi.org/10.1016/j.patrec.2006.07.009] ], Xu in 2007 [6Z.S. Xu, "Some similarity measures of intuitionistic fuzzy sets and their applications to multiple attribute decision making", Fuzzy Optim. Decis. Making, vol. 6, pp. 109-121.
[http://dx.doi.org/10.1007/s10700-007-9004-z] ] and in 2008 [7Z.S. Xu, and R.R. Yager, "Intuitionistic and interval-valued intuitionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group", Fuzzy Optim. Decis. Making, vol. 8, pp. 123-139.
[http://dx.doi.org/10.1007/s10700-009-9056-3] ] developed some similarity measures on IFSs. Li et al. introduced a new axiomatic definition of a similarity measure for IFSs. Later, Mitchell in 2003 developed a statistical approach as an extension of Li’s similarity measure and introduced some examples [8H.B. Mitchell, "On the Dengfeng-Chuntian similarity measure and its application to pattern recognition", Pattern Recognit. Lett., vol. 24, pp. 3101-3104.
[http://dx.doi.org/10.1016/S0167-8655(03)00169-7] ]. Hung and Yang in 2004 generalized the Hausdorff distance and proposed three new similarity measures on IFSs [9W.L. Hung, and M.S. Yang, "Similarity measures of intuitionistic fuzzy sets based on Hausdorff distance", Pattern Recognit. Lett., vol. 25, pp. 1603-1611.
[http://dx.doi.org/10.1016/j.patrec.2004.06.006] ]. Using the cosine function, Ye in 2011 proposed a new similarity measure and a weighted similarity measure [10J. Ye, "Cosine similarity measures for intuitionistic fuzzy sets and their applications", Math. Comput. Model., vol. 53, pp. 91-97.
[http://dx.doi.org/10.1016/j.mcm.2010.07.022] ]. Hwang et al. in 2012, presented a new similarity measure by utilizing Sugeno integral and used in clustering analysis [11C.M. Hwang, M.S. Yang, W.L. Hung, and M.G. Lee, "A similarity measure of intuitionistic fuzzy sets based on the Sugeno integral with its application to pattern recognition", Inf. Sci., vol. 189, pp. 93-109.
[http://dx.doi.org/10.1016/j.ins.2011.11.029] ]. Xu in 2007 developed some similarity measures and used it in multi-criteria decision-making problems [6Z.S. Xu, "Some similarity measures of intuitionistic fuzzy sets and their applications to multiple attribute decision making", Fuzzy Optim. Decis. Making, vol. 6, pp. 109-121.
[http://dx.doi.org/10.1007/s10700-007-9004-z] ]. A general type of similarity measure [12F.E. Boran, and D. Akay, "A biparametric similarity measure on intuitionistic fuzzy sets with applications to pattern recognition", Inf. Sci., vol. 255, pp. 45-57.
[http://dx.doi.org/10.1016/j.ins.2013.08.013] ] was developed by Boran and Akay in 2014 that connects two parameters norm and the level of uncertainty. An axiomatic approach of the similarity measure of IFS [13J. Li, G. Deng, H. Li, and W. Zeng, "The relationship between similarity measure and entropy of intuitionistic fuzzy sets", Inf. Sci., vol. 188, pp. 314-321.
[http://dx.doi.org/10.1016/j.ins.2011.11.021] ] was developed by Li et al. in 2012.

Distance measures and similarity measures have some significance and importance in decision-making situations. Many researchers are also studied and developed several distance measures and used in various field of decision-making situations. Szmidt and Kacprzyk in 2000 developed the Hamming distance measure and Euclidean distance measure extending the original Hamming and Euclidean distance measure [14E. Szmidt, and J. Kacprzyk, "Distances between intuitionistic fuzzy sets", Fuzzy Sets Syst., vol. 114, pp. 505-518.
[http://dx.doi.org/10.1016/S0165-0114(98)00244-9] ]. Later, Grzegorzewski in 2004 developed the Hausdorff distance measure between two IFSs [15P. Grzegorzewski, "Distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets based on the Hausdorff_metric", Fuzzy Sets and Syst, vol. 148, pp. 319-328. doi:10.1016/j.fss.2003.08.005 48-59. doi: 10.1016/j.asoc.2017.03.046]. Then, Szmidt and Kacprzyk, in 2004 proposed a distance measure for IFSs [16E. Szmidt, and J. Kacprzyk, "A similarity measure for intuitionistic fuzzy sets and its application in sup-porting medical diagnostic reasoning", Arti_cial Intelligence and Soft Computing - ICAISC 2004, Lect. Notes Comput. Sci., vol. 3070, pp. 388-393.
[http://dx.doi.org/10.1007/978-3-540-24844-6 56] ]. Wang and Xin in 2005 developed a new distance measure [17J.H. Park, K.M. Lim, and Y.C. Kwun, "Distance measure between intuitionistic fuzzy sets and its application to pattern recognition", Korean Inst. Intell. Syst., vol. 19, pp. 556-561.
[http://dx.doi.org/10.5391/JKIIS.2009.19.4.556] ] using the Hausdorff distance measure developed by Grzegorzewski. In a similar way, Park et al. in 2009 also developed a new distance measure [18W. Wang, and X. Xin, "Distance measure between intuitionistic fuzzy sets", Pattern Recognit. Lett., vol. 26, pp. 2063-2069.
[http://dx.doi.org/10.1016/j.patrec.2005.03.018] ] as an extension of distance measure developed by Wang and Xin. Then, Maheshwari and Srivastava in 2016 proposed a new distance measure [19S. Maheshwari, and A. Srivastava, "Study on divergence measures for intuitionistic fuzzy sets and its application in medical diagnosis", J. Appl. Anal. Comput., vol. 6, pp. 772-789.
[http://dx.doi.org/10.11948/2016050] ] using the logarithmic function. Ngan et al., in 2018 proposed the HMax-distance measure between two IFSs [20R.T. Ngana, L.H. Sonb, B.C. Cuongc, and M. Alid, "H-max distance measure of intuitionistic fuzzy sets in decision making", applied soft computing, .
[http://dx.doi.org/10.1016/j.asoc.2018.04.036] ].

1.1. Motivation for this Study

There are several studies carried out to make a decision support system for medical diagnosis using fuzzy similarity and fuzzy distance measure. Though in literature, there are several numbers of distance measures, it is always necessary to have a sufficient number of distance measures to check and validate the results by applying different distance measures to obtain more reliable and convenient result. In addition, the results obtained by some earlier studies [21S.K. De, R. Biswas, and A.R. Roy, "An application of intuitionistic fuzzy sets in medical diagnosis", Fuzzy Sets Syst., vol. 117, pp. 209-213.
[http://dx.doi.org/10.1016/S0165-0114(98)00235-8] , 20R.T. Ngana, L.H. Sonb, B.C. Cuongc, and M. Alid, "H-max distance measure of intuitionistic fuzzy sets in decision making", applied soft computing, .
[http://dx.doi.org/10.1016/j.asoc.2018.04.036] , 16E. Szmidt, and J. Kacprzyk, "A similarity measure for intuitionistic fuzzy sets and its application in sup-porting medical diagnostic reasoning", Arti_cial Intelligence and Soft Computing - ICAISC 2004, Lect. Notes Comput. Sci., vol. 3070, pp. 388-393.
[http://dx.doi.org/10.1007/978-3-540-24844-6 56] ] are not relevant and contradicts with each other. Also, a recent study [20R.T. Ngana, L.H. Sonb, B.C. Cuongc, and M. Alid, "H-max distance measure of intuitionistic fuzzy sets in decision making", applied soft computing, .
[http://dx.doi.org/10.1016/j.asoc.2018.04.036] ] shows more appropriate and relevant result which are different from the aforementioned studies. These are the main motivation for us to study in this particular topic.

In this paper, a new distance measure on Intuitionistic fuzzy set has been introduced and used in an existing data set of medical diagnosis studies to show the usability of the proposed distance measure. In the introduction section, the general view of uncertainty in medical diagnosis and the literature review on existing studies of medical diagnosis using IFS, similarity and distance measure has been given. In the preliminary section, the basic concepts and definitions of Intuitionistic fuzzy set theory are explained. The explanations and definitions of existing and well-known distance measures are given in section 3. In the next section, i.e. section 4, a new distance measure on Intuitionistic fuzzy sets has been proposed and proved that the proposed distance measure satisfies all necessary conditions. In section 5, a methodology has been discussed to determine the possible disease suffered by any patient using intuitionistic fuzzy set and the proposed distance measure. In section 6, a case study is carried out on existing data sets taken by some earlier researchers. In section 7, a discussion on the obtained result has been elaborated and compared with existing and recent studies and found that the proposed distance measure produces more relevant results.

2. PRELIMINARY

In this section, the basic concepts of fuzzy set, intuitionistic fuzzy sets, and intuitionistic fuzzy distance measures have been discussed.

2.1. Definition: Fuzzy Set [1L.A. Zadeh, "Fuzzy sets", Inf. Control, vol. 8, pp. 338-353.
[http://dx.doi.org/10.1016/S0019-9958(65)90241-X] ]

A fuzzy set is one which assigns grades of membership between 0 and 1 to an object within its universe of discourse. If X is a universal set then a fuzzy set A is defined by its membership function.

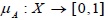2.2. Definition: Intuitionistic Fuzzy Set [2K.T. Atanassov, "Intuitionistic fuzzy sets", Fuzzy Sets Syst., vol. 20, pp. 87-96.
[http://dx.doi.org/10.1016/S0165-0114(86)80034-3] ]

An Intuitionistic fuzzy set A on a universe of discourse X is defined as

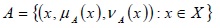Where 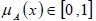is called the “degree of membership” of x in A, 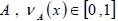is called the “degree of non-membership” of x in A, and 0 ≤ µA(x) + µA(x) ≤ 1.

Here, πA(x) = 1 - µA(x) - vA(x) is called hesitancy of x. πA(x) can be considered as the degree of lack of commitment or uncertainty associated with the membership or non-membership in A.

In IFS, each element is assigned to a membership degree and a non-membership degree, whereas FST only assigns each element a membership degree. For this reason, IFS has been used more than the FST to deal with the uncertainty efficiently.

Definition: Let 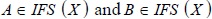then:

a)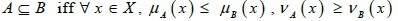

b)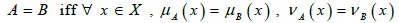

c) 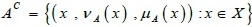, Where Ac is the complement of A.

d)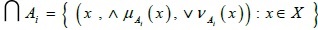

e)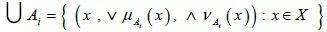

Definition: Let d denote a mapping d: IFS x IFS → [0, 1], if d (A, B) satisfies the following properties, d (A, B) is called the distance between .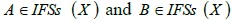

a) 0 ≤ d ≤ 1

b) d (A, B)if and only if A = B

c) d (A, B) = D (B, A)

d) d (A, C) ≤ d (A, B) + d (B, C)

3. SOME WELL-KNOWN DISTANCE MEASURES

Let 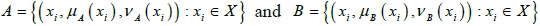be two IFSs, then some well-known distance measures are given below:

  1. The normalized Hamming distance [14E. Szmidt, and J. Kacprzyk, "Distances between intuitionistic fuzzy sets", Fuzzy Sets Syst., vol. 114, pp. 505-518.
    [http://dx.doi.org/10.1016/S0165-0114(98)00244-9]     ]: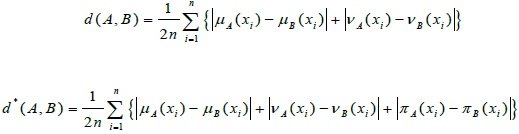
  2. The normalized Euclidean distance [14E. Szmidt, and J. Kacprzyk, "Distances between intuitionistic fuzzy sets", Fuzzy Sets Syst., vol. 114, pp. 505-518.
    [http://dx.doi.org/10.1016/S0165-0114(98)00244-9]     ]: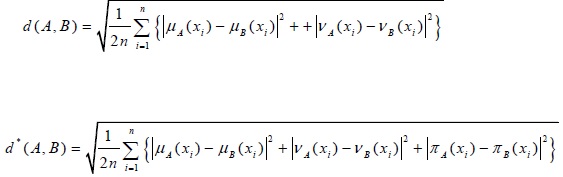
  3. The distance measure of two IFSs [16E. Szmidt, and J. Kacprzyk, "A similarity measure for intuitionistic fuzzy sets and its application in sup-porting medical diagnostic reasoning", Arti_cial Intelligence and Soft Computing - ICAISC 2004, Lect. Notes Comput. Sci., vol. 3070, pp. 388-393.
    [http://dx.doi.org/10.1007/978-3-540-24844-6 56]     ]: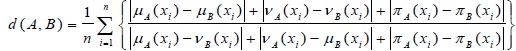
  4. The Hausdorff distance measure of two IFSs [15P. Grzegorzewski, "Distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets based on the Hausdorff_metric", Fuzzy Sets and Syst, vol. 148, pp. 319-328. doi:10.1016/j.fss.2003.08.005 48-59. doi: 10.1016/j.asoc.2017.03.046]:
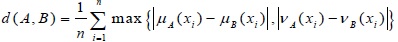
  5. The distance measure of two IFSs is proposed by [17J.H. Park, K.M. Lim, and Y.C. Kwun, "Distance measure between intuitionistic fuzzy sets and its application to pattern recognition", Korean Inst. Intell. Syst., vol. 19, pp. 556-561.
    [http://dx.doi.org/10.5391/JKIIS.2009.19.4.556]     ]: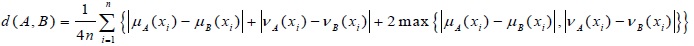
  6. The distance measure of two IFSs is proposed by [18W. Wang, and X. Xin, "Distance measure between intuitionistic fuzzy sets", Pattern Recognit. Lett., vol. 26, pp. 2063-2069.
    [http://dx.doi.org/10.1016/j.patrec.2005.03.018]     ]: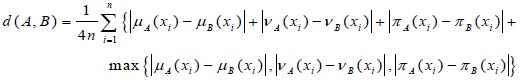
  7. The divergence measure of two IFSs is proposed by [19S. Maheshwari, and A. Srivastava, "Study on divergence measures for intuitionistic fuzzy sets and its application in medical diagnosis", J. Appl. Anal. Comput., vol. 6, pp. 772-789.
    [http://dx.doi.org/10.11948/2016050]     ]: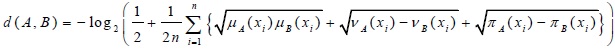
  8. The H-max distance measures of intuitionistic fuzzy sets is given by [20R.T. Ngana, L.H. Sonb, B.C. Cuongc, and M. Alid, "H-max distance measure of intuitionistic fuzzy sets in decision making", applied soft computing, .
    [http://dx.doi.org/10.1016/j.asoc.2018.04.036]     ]: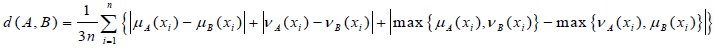
  9. WX-Hmax distance measures of intuitionistic fuzzy sets is given by [20R.T. Ngana, L.H. Sonb, B.C. Cuongc, and M. Alid, "H-max distance measure of intuitionistic fuzzy sets in decision making", applied soft computing, .
    [http://dx.doi.org/10.1016/j.asoc.2018.04.036]     ]: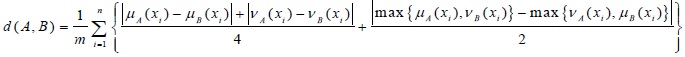

4. A NOVEL DISTANCE MEASURE ON INTUITIONISTIC FUZZY SETS

Let X = {x1, x2,....xn} be the universe of discourse. Let 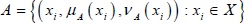and 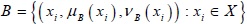be two IFSs. Then the new distance measure can be defined as:

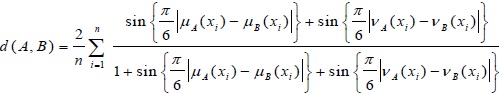All the necessary four conditions to be a distance measure are satisfied by the new distance measure and the proof is given below:

(a) 0 ≤ d (A, B) ≤ 1

Proof (a): As we know, 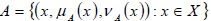for degree of membership 0 ≤ µA (x) ≤ 1 and degree of non-membership 0 ≤ vA (x) ≤ 1.

This implies for 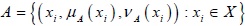and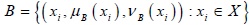

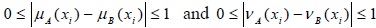
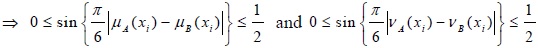
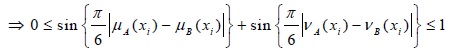(1)

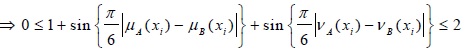(2)

Therefore, from Eq. (1) and Eq. (2)

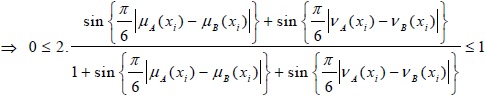
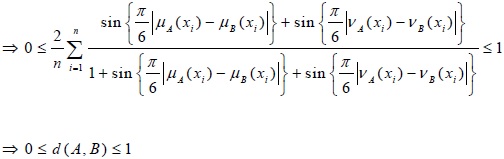
(b) d (A, B) = 0 if and only if A = B

Proof: d (A, B = 0)

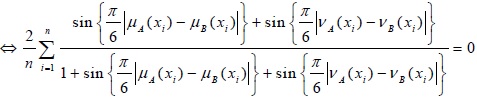
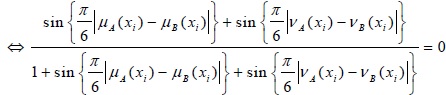
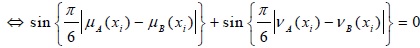
For, this reason

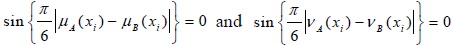
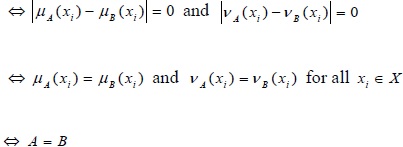
Hence, d (A, B) = 0 if and only if A = B.

(c) d (A, B) = d (B, A)

Proof (c):

d (A, B)

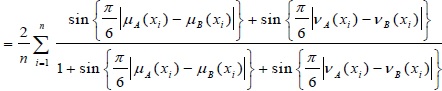
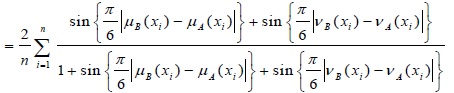
= d (B, A)

To prove the triangular inequality we have to use the following trigonometric inequality:

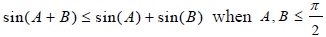Proof:

sin (A) + sin (B) - sin (A + B)

= sin A + sin B - sin A cos B - sin B cos A

= sin A (1 - = cos B) + sin B (1 - = cos A) ≥ 0

Since sin A, sin B, 1 - cos A ≥ 0 for A, A ≤ .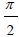

sin (A) + sin (B) - sin (A + B) ≥ 0

sin (A + B) ≤ sin (A) + sin (B) when A, B ≤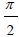

(d) If A, BandC be three intuitionistic fuzzy sets, then the distance measure satisfies the triangular inequality. Ie. d(A, C) ≤ d(A, B) + d(B, C).

Proof (d): Consider, 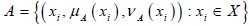, 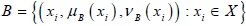and 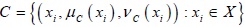be three intuitionistic fuzzy sets.

Now, from the basic inequality of real numbers we know that:

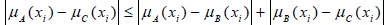
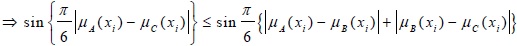
(3)

Eq. (3)

(since sin (A + B) ≤ sin (A) + sin (B) when A, B ≤ ; from above trigonometric inequality)

Similarly,

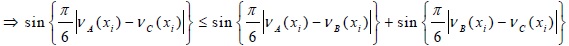(4)

Adding Eq.(3) and Eq.(4) we get

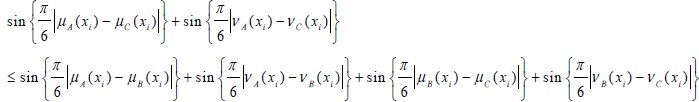
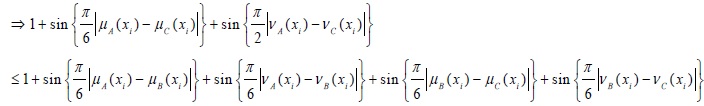
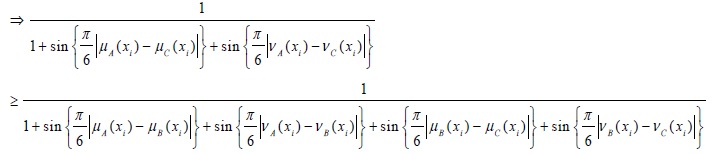
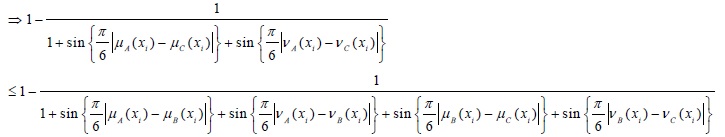
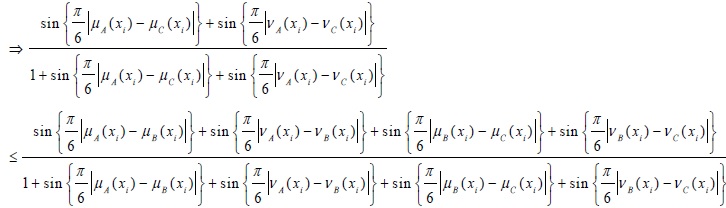
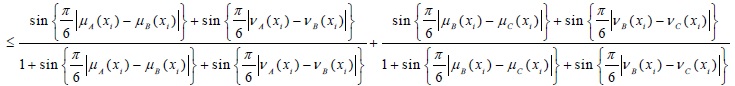
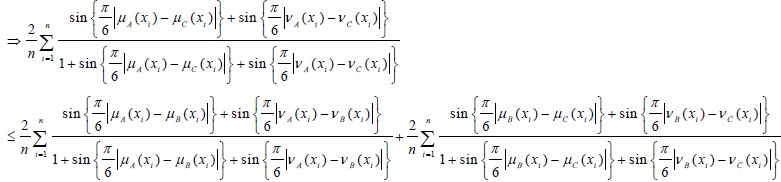
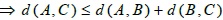
Thus, it is clear that the proposed distance measure satisfies all the metric properties.

5. METHODOLOGY

Let us consider {D1, D2,..., Dm} be a set of number of possible diseases and {P1, P2,..., Pn} be a set of n number of patients. As stated earlier, symptoms for different diseases as well as symptoms of the patients are expressed in linguistic expressions most of the time. For this reason, uncertainty and fuzziness exist for the expression of the symptoms of the patients and disease. So, to express the symptoms, IFSs has been used.

Let 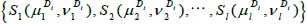be the symptoms the disease Di and 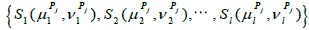be the symptoms of patient Pj expressed in IFSs. Therefore, the distance between the symptoms the disease Di and symptoms of patient Pj can be evaluated as follows using the proposed distance measure:

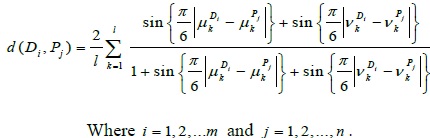The distances between each pair of disease and patients can be represented with the help of the following matrix:

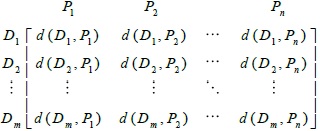Now, distance measures can be used to select the disease suffered by patient. Using the fact that, less distance between two IFSs implies more similarity between them, it can be said that for the patient Pj the disease most possibly suffered by him or her is the disease corresponding to .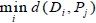

6. A CASE STUDY IN MEDICAL DIAGNOSIS

In this case study, the proposed distance measure has been applied in a decision-making problem of medical diagnosis. The data are taken from the study carried out by De et al., in 2001 [21S.K. De, R. Biswas, and A.R. Roy, "An application of intuitionistic fuzzy sets in medical diagnosis", Fuzzy Sets Syst., vol. 117, pp. 209-213.
[http://dx.doi.org/10.1016/S0165-0114(98)00235-8] ]. In this case study, we consider a set of symptoms S, a set of diagnosis D and a set of patients P. Let P = {Arman, Bijit, Chandra, Deva}, S = {Temperature, Headache, Stomach pain, Cough, Chest pain} and D = {Viral fever, Malaria, Typhoid Stomach pain, Chest problem}. Our objective is to carry out the right decision of diagnosis for each patient, from the set of symptoms, for each disease.

The relation between symptom and disease and relation between patient and symptom is given in Tables 1 and 2, respectively.

Table 1
Symptoms-diseases intuitionistic fuzzy relation.


Table 2
Patients- symptoms intuitionistic fuzzy relation.


Now, we can represent the fevers as intuitionistic fuzzy sets for symptoms.

Similarly, we can represent the patients as intuitionistic fuzzy sets as follows:

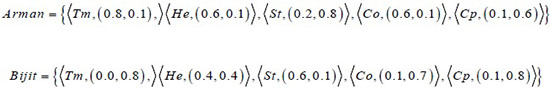
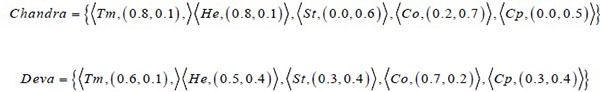
Now, the intuitionistic distance is measured between the disease and the patients in terms of their symptoms.

d (Vf, Arman)

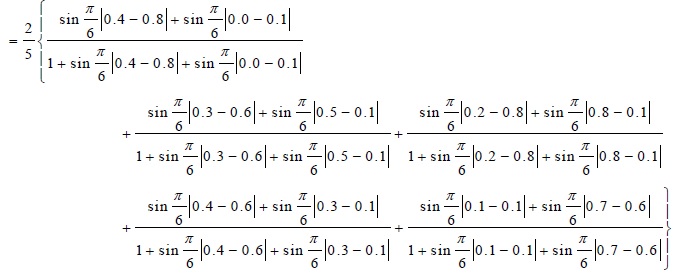
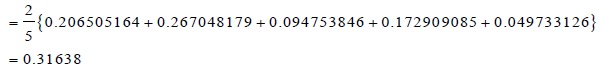
d (Vf, Bijit)

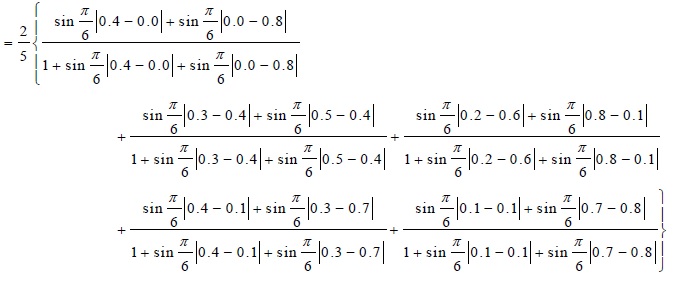
d (Vf, Chandra)

d (Vf, Deva)

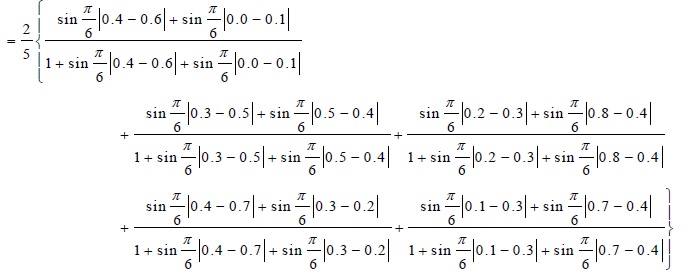
Similarly, the intuitionistic distance measure between the patients and the diseases can be found as:

In short, with the help of the following distance matrix, it can be shown to what extent the symptoms of disease differ by the symptoms of patients.

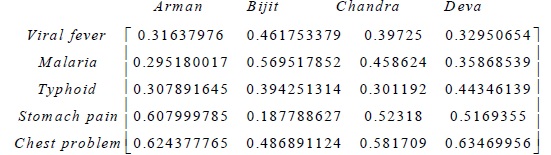
As due to the fact, less distance between patient and disease implies more possibility of having the disease, we can predict which disease is suffered by the four people. From the distance matrix, one can observe that, if the doctor agrees Arman suffers from Malaria, Bijit suffers from stomach pain, Chandra suffers from Typhoid and Deva suffers from viral fever.

Now, in the following table, the comparison has been given between the results obtained by different researchers and the results obtained using our proposed distance measures.

From Tables 3 comparison has been made and it is observed that the results obtained by using our proposed distance measure are similar with results obtained by (Ngan et al. [20R.T. Ngana, L.H. Sonb, B.C. Cuongc, and M. Alid, "H-max distance measure of intuitionistic fuzzy sets in decision making", applied soft computing, .
[http://dx.doi.org/10.1016/j.asoc.2018.04.036] ], and Szmidt and Kacprzyk [14E. Szmidt, and J. Kacprzyk, "Distances between intuitionistic fuzzy sets", Fuzzy Sets Syst., vol. 114, pp. 505-518.
[http://dx.doi.org/10.1016/S0165-0114(98)00244-9] ].

Table 3
Comparison of existing results with the proposed distance measure.


CONCLUSION

The objective of this paper is to develop a new distance measure for intuitionistic fuzzy sets, which is achieved. The novelty and efficiency has been established by applying the proposed distance measure in medical diagnosis making problem. The result which is evaluated using the new distance measure coincides with the earlier advance approaches. This shows the reliability and validity of the proposed distance measures.

As a future work, it will be beneficial to extend the proposed distance measure in a generalized form and use in the development of fuzzy decision-making problems in medical diagnosis.

CONSENT FOR PUBLICATION

Not applicable.

CONFLICT OF INTEREST

The authors confirm that this article content has no conflict of interest.

ACKNOWLEGEMENTS

Declared none.

REFERENCES
[1] L.A. Zadeh, "Fuzzy sets", Inf. Control, vol. 8, pp. 338-353.
[http://dx.doi.org/10.1016/S0019-9958(65)90241-X]
[2] K.T. Atanassov, "Intuitionistic fuzzy sets", Fuzzy Sets Syst., vol. 20, pp. 87-96.
[http://dx.doi.org/10.1016/S0165-0114(86)80034-3]
[3] D.F. Li, and C.T. Cheng, "New similarity measures of intuitionistic fuzzy sets and application to pattern recognitions", Pattern Recognit. Lett., vol. 23, pp. 221-225.
[http://dx.doi.org/10.1016/S0167-8655(01)00110-6]
[4] Z.Z. Liang, and P.F. Shi, "Similarity measures on intuitionistic fuzzy sets", Pattern Recognit. Lett., vol. 24, pp. 2687-2693.
[http://dx.doi.org/10.1016/S0167-8655(03)00111-9]
[5] Y. Li, D.L. Olson, and Z. Qin, "Similarity measures between intuitionistic fuzzy (vague) sets: A comparative analysis", Pattern Recognit. Lett., vol. 28, pp. 278-285.
[http://dx.doi.org/10.1016/j.patrec.2006.07.009]
[6] Z.S. Xu, "Some similarity measures of intuitionistic fuzzy sets and their applications to multiple attribute decision making", Fuzzy Optim. Decis. Making, vol. 6, pp. 109-121.
[http://dx.doi.org/10.1007/s10700-007-9004-z]
[7] Z.S. Xu, and R.R. Yager, "Intuitionistic and interval-valued intuitionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group", Fuzzy Optim. Decis. Making, vol. 8, pp. 123-139.
[http://dx.doi.org/10.1007/s10700-009-9056-3]
[8] H.B. Mitchell, "On the Dengfeng-Chuntian similarity measure and its application to pattern recognition", Pattern Recognit. Lett., vol. 24, pp. 3101-3104.
[http://dx.doi.org/10.1016/S0167-8655(03)00169-7]
[9] W.L. Hung, and M.S. Yang, "Similarity measures of intuitionistic fuzzy sets based on Hausdorff distance", Pattern Recognit. Lett., vol. 25, pp. 1603-1611.
[http://dx.doi.org/10.1016/j.patrec.2004.06.006]
[10] J. Ye, "Cosine similarity measures for intuitionistic fuzzy sets and their applications", Math. Comput. Model., vol. 53, pp. 91-97.
[http://dx.doi.org/10.1016/j.mcm.2010.07.022]
[11] C.M. Hwang, M.S. Yang, W.L. Hung, and M.G. Lee, "A similarity measure of intuitionistic fuzzy sets based on the Sugeno integral with its application to pattern recognition", Inf. Sci., vol. 189, pp. 93-109.
[http://dx.doi.org/10.1016/j.ins.2011.11.029]
[12] F.E. Boran, and D. Akay, "A biparametric similarity measure on intuitionistic fuzzy sets with applications to pattern recognition", Inf. Sci., vol. 255, pp. 45-57.
[http://dx.doi.org/10.1016/j.ins.2013.08.013]
[13] J. Li, G. Deng, H. Li, and W. Zeng, "The relationship between similarity measure and entropy of intuitionistic fuzzy sets", Inf. Sci., vol. 188, pp. 314-321.
[http://dx.doi.org/10.1016/j.ins.2011.11.021]
[14] E. Szmidt, and J. Kacprzyk, "Distances between intuitionistic fuzzy sets", Fuzzy Sets Syst., vol. 114, pp. 505-518.
[http://dx.doi.org/10.1016/S0165-0114(98)00244-9]
[15] P. Grzegorzewski, "Distances between intuitionistic fuzzy sets and/or interval-valued fuzzy sets based on the Hausdorff_metric", Fuzzy Sets and Syst, vol. 148, pp. 319-328. doi:10.1016/j.fss.2003.08.005 48-59. doi: 10.1016/j.asoc.2017.03.046
[16] E. Szmidt, and J. Kacprzyk, "A similarity measure for intuitionistic fuzzy sets and its application in sup-porting medical diagnostic reasoning", Arti_cial Intelligence and Soft Computing - ICAISC 2004, Lect. Notes Comput. Sci., vol. 3070, pp. 388-393.
[http://dx.doi.org/10.1007/978-3-540-24844-6 56]
[17] J.H. Park, K.M. Lim, and Y.C. Kwun, "Distance measure between intuitionistic fuzzy sets and its application to pattern recognition", Korean Inst. Intell. Syst., vol. 19, pp. 556-561.
[http://dx.doi.org/10.5391/JKIIS.2009.19.4.556]
[18] W. Wang, and X. Xin, "Distance measure between intuitionistic fuzzy sets", Pattern Recognit. Lett., vol. 26, pp. 2063-2069.
[http://dx.doi.org/10.1016/j.patrec.2005.03.018]
[19] S. Maheshwari, and A. Srivastava, "Study on divergence measures for intuitionistic fuzzy sets and its application in medical diagnosis", J. Appl. Anal. Comput., vol. 6, pp. 772-789.
[http://dx.doi.org/10.11948/2016050]
[20] R.T. Ngana, L.H. Sonb, B.C. Cuongc, and M. Alid, "H-max distance measure of intuitionistic fuzzy sets in decision making", applied soft computing, .
[http://dx.doi.org/10.1016/j.asoc.2018.04.036]
[21] S.K. De, R. Biswas, and A.R. Roy, "An application of intuitionistic fuzzy sets in medical diagnosis", Fuzzy Sets Syst., vol. 117, pp. 209-213.
[http://dx.doi.org/10.1016/S0165-0114(98)00235-8]
Track Your Manuscript:


Endorsements



"Open access will revolutionize 21st century knowledge work and accelerate the diffusion of ideas and evidence that support just in time learning and the evolution of thinking in a number of disciplines."


Daniel Pesut
(Indiana University School of Nursing, USA)

"It is important that students and researchers from all over the world can have easy access to relevant, high-standard and timely scientific information. This is exactly what Open Access Journals provide and this is the reason why I support this endeavor."


Jacques Descotes
(Centre Antipoison-Centre de Pharmacovigilance, France)

"Publishing research articles is the key for future scientific progress. Open Access publishing is therefore of utmost importance for wider dissemination of information, and will help serving the best interest of the scientific community."


Patrice Talaga
(UCB S.A., Belgium)

"Open access journals are a novel concept in the medical literature. They offer accessible information to a wide variety of individuals, including physicians, medical students, clinical investigators, and the general public. They are an outstanding source of medical and scientific information."


Jeffrey M. Weinberg
(St. Luke's-Roosevelt Hospital Center, USA)

"Open access journals are extremely useful for graduate students, investigators and all other interested persons to read important scientific articles and subscribe scientific journals. Indeed, the research articles span a wide range of area and of high quality. This is specially a must for researchers belonging to institutions with limited library facility and funding to subscribe scientific journals."


Debomoy K. Lahiri
(Indiana University School of Medicine, USA)

"Open access journals represent a major break-through in publishing. They provide easy access to the latest research on a wide variety of issues. Relevant and timely articles are made available in a fraction of the time taken by more conventional publishers. Articles are of uniformly high quality and written by the world's leading authorities."


Robert Looney
(Naval Postgraduate School, USA)

"Open access journals have transformed the way scientific data is published and disseminated: particularly, whilst ensuring a high quality standard and transparency in the editorial process, they have increased the access to the scientific literature by those researchers that have limited library support or that are working on small budgets."


Richard Reithinger
(Westat, USA)

"Not only do open access journals greatly improve the access to high quality information for scientists in the developing world, it also provides extra exposure for our papers."


J. Ferwerda
(University of Oxford, UK)

"Open Access 'Chemistry' Journals allow the dissemination of knowledge at your finger tips without paying for the scientific content."


Sean L. Kitson
(Almac Sciences, Northern Ireland)

"In principle, all scientific journals should have open access, as should be science itself. Open access journals are very helpful for students, researchers and the general public including people from institutions which do not have library or cannot afford to subscribe scientific journals. The articles are high standard and cover a wide area."


Hubert Wolterbeek
(Delft University of Technology, The Netherlands)

"The widest possible diffusion of information is critical for the advancement of science. In this perspective, open access journals are instrumental in fostering researches and achievements."


Alessandro Laviano
(Sapienza - University of Rome, Italy)

"Open access journals are very useful for all scientists as they can have quick information in the different fields of science."


Philippe Hernigou
(Paris University, France)

"There are many scientists who can not afford the rather expensive subscriptions to scientific journals. Open access journals offer a good alternative for free access to good quality scientific information."


Fidel Toldrá
(Instituto de Agroquimica y Tecnologia de Alimentos, Spain)

"Open access journals have become a fundamental tool for students, researchers, patients and the general public. Many people from institutions which do not have library or cannot afford to subscribe scientific journals benefit of them on a daily basis. The articles are among the best and cover most scientific areas."


M. Bendandi
(University Clinic of Navarre, Spain)

"These journals provide researchers with a platform for rapid, open access scientific communication. The articles are of high quality and broad scope."


Peter Chiba
(University of Vienna, Austria)

"Open access journals are probably one of the most important contributions to promote and diffuse science worldwide."


Jaime Sampaio
(University of Trás-os-Montes e Alto Douro, Portugal)

"Open access journals make up a new and rather revolutionary way to scientific publication. This option opens several quite interesting possibilities to disseminate openly and freely new knowledge and even to facilitate interpersonal communication among scientists."


Eduardo A. Castro
(INIFTA, Argentina)

"Open access journals are freely available online throughout the world, for you to read, download, copy, distribute, and use. The articles published in the open access journals are high quality and cover a wide range of fields."


Kenji Hashimoto
(Chiba University, Japan)

"Open Access journals offer an innovative and efficient way of publication for academics and professionals in a wide range of disciplines. The papers published are of high quality after rigorous peer review and they are Indexed in: major international databases. I read Open Access journals to keep abreast of the recent development in my field of study."


Daniel Shek
(Chinese University of Hong Kong, Hong Kong)

"It is a modern trend for publishers to establish open access journals. Researchers, faculty members, and students will be greatly benefited by the new journals of Bentham Science Publishers Ltd. in this category."


Jih Ru Hwu
(National Central University, Taiwan)

Browse Contents




Webmaster Contact: info@benthamopen.net
Copyright © 2023 Bentham Open