- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Cybernetics & Systemics Journal
(Discontinued)
ISSN: 1874-110X ― Volume 12, 2018
Decision Analysis Simulation of a Low Carbon Supply Chain System based on Different Risk Aversion Models Running on Matlab
Xuemei Zhang*, Jianhua Yan, Wei Shi
Abstract
Objective:
The decision problem of a low carbon supply chain system comprising one manufacturer and one retailer under different risk aversion models is studied through comparative simulation analysis of decentralized and centralized decision models.
Method:
The influences of the risk aversion coefficient, consumer low carbon preference and carbon emission reduction cost coefficient on decision outcomes within the supply chain system are analyzed.
Results:
The research results show that when the retailer is completely risk averse, the decentralized decision model can achieve the same utility as the centralized decision model without using the coordination contract. When the manufacturer is risk neutral and the retailer is risk averse, the wholesale price under the decentralized decision model is lower than under the centralized decision model because a preference exists for low carbon and a reduction occurs in carbon emission.
Conclusion:
Under a different risk aversion coefficient, the consumer low carbon preference coefficient and carbon emission cost coefficient have the same influence on the decision variables of the manufacturer and the retailer. Moreover, the decision variables correlate positively with the low carbon preference coefficient and are negatively related to the carbon emission reduction cost coefficient. Under different risk aversion models, the dual marginal utility caused by the decentralized decision model can be alleviated through risk aversion. The revenue sharing contract is then designed to perfectly coordinate the low carbon supply chain system. Finally, numerical simulation was used to analyze the manufacturer’s risk aversion coefficient, carbon emission reduction cost coefficient and consumer low carbon preference coefficient based on the results of the optimal decision running on Matlab.
Article Information
Identifiers and Pagination:
Year: 2018Volume: 12
First Page: 150
Last Page: 165
Publisher Id: TOCSJ-12-150
DOI: 10.2174/1874110X01812010150
Article History:
Received Date: 9/7/2018Revision Received Date: 17/8/2018
Acceptance Date: 21/8/2018
Electronic publication date: 30/10/2018
Collection year: 2018
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: (https://creativecommons.org/licenses/by/4.0/legalcode). This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
* Address correspondence to this author at the School of Business, Anhui Provincial Key Laboratory of Regional Logistics Planning and Modern Logistics Engineering, Fuyang Normal University, No. 100 Qinghe West Road, Fu Yang 236037, China; Tel: +8613966555561; E-mail: xmz@mail.ustc.edu.cn
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 9-7-2018 |
Original Manuscript | Decision Analysis Simulation of a Low Carbon Supply Chain System based on Different Risk Aversion Models Running on Matlab | |
1. INTRODUCTION
As China’s economy continues to develop, environmental protection and ecological construction have become increasingly important in economic and social development planning. Sustainable development is strongly emphasized, particularly a low carbon economy with low energy consumption and low pollution [1J. Chen, "Study on supply chain management in a Low carbon era", J. Syst. Manage., vol. 21, no. 6, pp. 721-728.]. To achieve sustainable development, the study of low carbon supply chain system has attracted considerable attention in academia.
Research on low carbon supply chain system mainly focuses on the pricing and coordination of low carbon supply chain system and decision-making regarding carbon emission reduction levels. Based on the summary of current research on supply chain system management, Chen [1J. Chen, "Study on supply chain management in a Low carbon era", J. Syst. Manage., vol. 21, no. 6, pp. 721-728.] noted several important directions of supply chain system management under a low carbon background. Mao et al. [2Z.F. Mao, S. Zhang, and X.M. Li, "Low carbon supply chain firm integration and firm performance in China", J. Clean. Prod., vol. 153, no. 1, pp. 354-361.
[http://dx.doi.org/10.1016/j.jclepro.2016.07.081] ] analyzed the relationship between internal low carbon integration and external low carbon integration and firm performance and noted that internal low carbon integration improves corporate environmental performance but simultaneously hinders financial performance. Zu et al. [3Y.F. Zu, L.H. Chen, and Y. Fan, "Research on low-carbon strategies in supply chain with environmental regulations based on differential game", J. Clean. Prod., vol. 177, no. 10, pp. 527-546.
[http://dx.doi.org/10.1016/j.jclepro.2017.12.220] ] researched low carbon strategies in a supply chain system with three progressive environmental regulation situations using a Stackelberg game. By considering a two-level supply chain system comprising two manufacturers of low carbon and common products and a single retailer, Xu et al. [4C.Q. Xu, D.Z. Zhao, and B.Y. Yuan, "Study on coordination mechanisms and differential pricing of supply chain in low carbon environment", Oper. Res. Manage. Sci., vol. 24, no. 1, pp. 19-26.] discussed the problem of differential pricing and coordination mechanisms of supply chain systems. Under the single and double sales models, Cao et al. [5B.B. Cao, Z.D. Xiao, and C.Y. Zhu, "Study on supply chain decision under double sales model considering government low carbon policy", Chinese Journal of Management Science, vol. 26, no. 4, pp. 30-40.] studied the mechanism by which government price subsidies, one-time subsidies, and carbon taxes influence decisions in a low carbon supply chain system. Li et al. [6Y Li, and D Z Zhao, "Low-carbonization supply chain coordination with contracts considering fairness preference", Journal of Industrial Engineering / Engineering Management, vol. 29, no. 1, pp. 156-161.] studied the supply chain coordination problem of manufacturers who offer different preferences to retailers with a fair preference under a low carbon environment. Wang et al. [7Q.P. Wang, D.Z. Zhao, and L.F. He, "Contracting emission reduction for supply chains considering market low-carbon preference", J. Clean. Prod., vol. 120, no. 1, pp. 72-84.
[http://dx.doi.org/10.1016/j.jclepro.2015.11.049] ] focused on a dyadic supply chain system with a single manufacturer and retailer to develop a game model for studying issues of carbon emission reduction in the retailer dominant and power balanced cases, respectively. Under the assumption that consumers prefer low carbon products and voluntary emission reduction, Wang et al. [8Q.P. Wang, and D.Z. Zhao, "Revenue-sharing contract of supply chain based on consumer’s preference for low carbon products", Chinese Journal of Management Science, vol. 22, no. 9, pp. 106-113.] studied the decision problem of optimizing order level and reducing carbon emission for a retailer in a two-level supply chain system. Based on preference for low carbon consumption, Sun and Xiao [9J.N. Sun, and Z.D. Xiao, "Research on emission reduction strategy of low carbon supply chain considering consumer’s dual preferences", Chinese Journal of Management Science, vol. 26, no. 4, pp. 49-56.] subdivided consumer channel preferences and provided optimal emission reduction boundary conditions for the low carbon supply chain through the comparison and analysis of the decentralized and the centralized decision-making models. Hang et al. [10L.H. Zhang, G.W. Zhang, and R. Zhang, "Equilibrium contracts strategies of low carbon supply chain and high carbon supply chain", Computer Integrated Manufacturing Systems, vol. 24, no. 3, pp. 763-771.] researched the problem of low carbon technology and coordination strategy in market competition between two supply chain systems, one being high carbon and the other low carbon. The above research all focused more on the low carbon supply chain system decision with neutral manufacturers and retailers, which do not pay attention to risk aversion conditions.
Many manufacturers and retailers in supply chains are risk averse. In research on supply chain system decisions, some scholars have focused on risk aversion and supply chain decision-making. Xiao et al. [11T.J. Xiao, T.M. Choi, D.Q. Yang, and T.C.E. Cheng, "Service commitment strategy and pricing decisions in retail supply chains with risk-averse players", Serv. Sci., vol. 4, no. 3, pp. 236-252.
[http://dx.doi.org/10.1287/serv.1120.0021] ] researched the service commitment strategy and pricing decisions in a single-supplier single-retailer supply chain system where all players (including consumers) are risk averse. Ye et al. [12F. Ye, and Q. Lin, "Revenue sharing contract mechanisms of risk-averse supply chains", Journal of Industrial Engineering/ Engineering Management, vol. 26, no. 1, pp. 113-118.] studied the cooperation incentive problem of a two-level supply chain system, and analyzed the influence degree of the risk aversion coefficient of the supplier and retailer on the decision-making behavior and profit sharing coefficient of the two sides using empirical analysis. Ning et al. [13J. Ning, V. Babich, J. Handley, and J. Keppo, "Risk-aversion and B2B contracting under asymmetric information: Evidence from managed print services", Oper. Res., vol. 66, no. 2, pp. 392-408.
[http://dx.doi.org/10.1287/opre.2017.1673] ] investigated risk-aversion and B2B contracting under asymmetric information using evidence from managed print services. Dai et al. [14J.S. Dai, W.D. Meng, and B. Fan, "Supply chain coordination with risk aversion via buy-back contracts", Journal of Management Science in China, vol. 18, no. 5, pp. 57-65.] used CVaR to study the repurchase contract coordination problem with sales promotion effect and risk aversion supply chain. Xu et al. [15M.L. Xu, X.Z. Nie, and H.Y. Jian, "Pricing decision of dual-channel supply chain with risk preference", Control and Decision, vol. 31, no. 1, pp. 91-98.] explored the impact of risk preference on dual channel supply chain decision and established a pricing decision model of dual channel supply chain system based on the conditional risk value criterion. Liu et al. [16M.Q. Liu, E. Cao, and K. Salifou, "Pricing strategies of a dual-channel supply chain with risk aversion", Transp. Res., Part E Logist. Trans. Rev., vol. 90, no. 6, pp. 108-120.
[http://dx.doi.org/10.1016/j.tre.2015.11.007] ] studied the effect of risk aversion on the optimal policies of a dual-channel supply chain system under complete information and asymmetric information. Zhou et al. [17Y.W. Zhou, J.C. Li, and Y.G. Zhang, "Cooperative advertising and ordering policies in a two-echelon supply chain with risk-averse agents", Omega, vol. 75, no. 3, pp. 97-117.
[http://dx.doi.org/10.1016/j.omega.2017.02.005] ] considered a cooperative advertising and ordering issue in a two-echelon supply chain system in which a risk-averse manufacturer sells a product through a risk-averse retailer. Yan et al. [18B. Yan, Z.J. Jin, Y.P. Liu, and J.B. Yang, "Decision on risk-averse dual-channel supply chain under demand disruption", Commun. Nonlinear Sci. Numer. Simul., vol. 55, no. 2, pp. 206-224.
[http://dx.doi.org/10.1016/j.cnsns.2017.07.003] ] studied a dual-channel supply chain system using centralized and decentralized decision-making models and conducted a comparative analysis of decision-making before and after demand disruption. Yoo [19S.H. Yoo, "Product quality and return policy in a supply chain under risk aversion of a supplier", Int. J. Prod. Econ., vol. 154, no. 8, pp. 146-155.
[http://dx.doi.org/10.1016/j.ijpe.2014.04.012] ] considered an OEM supply chain system, where a buyer decides a return policy for consumers and delegates the product quality decision to a supplier, and identified the relationship between return policy and product quality decision in a decentralized system. In the dual channel supply chain system with random market demand, Zhang and Yao [20L.L. Zhang, and Z. Yao, "Optimal strategy of risk-averse dual-channel supply chain with consumer returns", Computer Integrated Manufacturing Systems, vol. 21, no. 3, pp. 766-775.] considered the optimal product pricing decision problem of the risk aversion dual channel supply chain system when the customer returns. Cao et al. [21X.G. Cao, B.R. Zheng, H.S. Xia, H. Wen, and J.Z. Li, "Analysis on closed-loop supply chain network equilibrium with risk-averse retailers", Control and Decision, vol. 29, no. 4, pp. 659-665.] studied the remanufacturing closed-loop supply chain system network equilibrium given a risk averse retailer under random demand condition. Using CVaR to measure risk, Dai et al. [22J.S. Dai, and W.D. Meng, "Revenue sharing contract for a risk-averse supply chain with promotional effect", Journal of Management Science in China, vol. 17, no. 5, pp. 25-34.] inspected the profit-sharing contract given a risk averse seller and the promotion effect. Gan et al. [23X.H. Gan, and K.F. Ying, "Vendor managed inventory contract model with risk averse", Syst. Eng., vol. 33, no. 1, pp. 116-121.] investigated the optimization and coordination of the supplier management inventory contract under random demand. The above researches pay little attention to the low carbon supply chain system decision problem under different risk aversion models.
Unlike the above literatures, this paper studied the low carbon supply chain decision problem under different risk aversion models. Specifically, the impacts of risk aversion coefficient and consumer preference for low carbon on carbon emission reduction level and the optimal decision of the supply chain system in the two-level low carbon supply chain are investigated. The decision results of the risk aversion low carbon supply chain system under centralized and decentralized decision-making are compared and simulated, and the revenue sharing contract is designed to realize the coordination of the low carbon supply chain system with risk averse participants.
2. PROBLEM DESCRIPTION AND BASIC HYPOTHESIS
We consider the case of a two-level supply chain comprising a manufacturer and a retailer, where the manufacturer sells only one product through the retailer, and both the manufacturer and the retailer are risk averse. It is assumed that consumers with low carbon preference are willing to pay a premium for low carbon products, even if this means they must increase their consumption investment. As hypothesized in the literature on the cost of carbon emission reduction [24C.T. Zhang, and L.P. Liu, "Research on coordination mechanism in three-level green supply chain under non-cooperative game", Appl. Math. Model., vol. 37, no. 5, pp. 3369-3379.
[http://dx.doi.org/10.1016/j.apm.2012.08.006] ], the cost increases with the size of the reduction, and the quadratic function is used to study the above precondition.
The symbols used in this study are as follows:
K : scale of uncertainty market demand, which has mean µ, and variance δ2;
α : price elasticity coefficient;
p : the retail price per unit of product;
w : the wholesale price per unit of product;
γ : strength of consumer preference for low carbon;
e : carbon emission reduction level;
cr : retailer selling cost per unit of product;
cm : manufacturer production cost per unit of product;
C(e) : cost of carbon emission reduction;
η : cost coefficient of carbon emission reduction;
βm : manufacturer risk aversion coefficient;
βr : retailer risk aversion coefficient;
π : random profit, the subscripts m, r, respectively, indicate the manufacturer and retailer;
U : utility function.
This paper makes the following basic assumptions: The product’s stochastic demand function is set to D = K - αp + γe; the cost of carbon emission reduction is set to 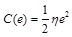 [24C.T. Zhang, and L.P. Liu, "Research on coordination mechanism in three-level green supply chain under non-cooperative game", Appl. Math. Model., vol. 37, no. 5, pp. 3369-3379.
[24C.T. Zhang, and L.P. Liu, "Research on coordination mechanism in three-level green supply chain under non-cooperative game", Appl. Math. Model., vol. 37, no. 5, pp. 3369-3379.
[http://dx.doi.org/10.1016/j.apm.2012.08.006] ]; α, η > 0.
The random profit of a risk averse retailer is,
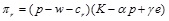 |
(1) |
The utility function of a risk averse retailer is,
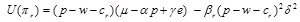 |
(2) |
Similarly, the random profit of a risk averse retailer is,
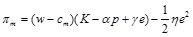 |
(3) |
The utility function of a risk averse retailer is,
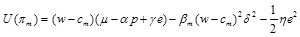 |
(4) |
In the following, the risk aversion supply chain system decision problem under centralized and decentralized decision-making will be analyzed, with the revenue sharing contract being designed to coordinate the risk aversion supply chain system.
3. THE SUPPLY CHAIN SYSTEM DECISION MODEL UNDER RISK AVERSION
3.1. The Decentralized Decision Model
In the decentralized decision-making model, supply chain system members pursue the maximization of their respective interests, and manufacturers and retailers engage in Stackelberg games in which the former dominate. The manufacturer first decides the wholesale price w and carbon emission level e, and then the retailer decides the retail price p. Therefore, the optimization model of the manufacturer can be expressed as,
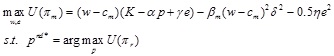 |
(5) |
The optimization model of the retailer can be expressed as,
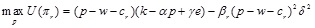 |
(6) |
Since 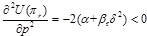 , U(πr) is the strict concave function of p. By setting
, U(πr) is the strict concave function of p. By setting 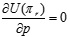 , the only optimal value pnd* can be obtained, and then by substituting pnd* into Eq.(4), we have U(πm) which is a function of w and e. For convenience of comparison, we set αη > γ2. Because
, the only optimal value pnd* can be obtained, and then by substituting pnd* into Eq.(4), we have U(πm) which is a function of w and e. For convenience of comparison, we set αη > γ2. Because 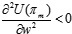 and
and 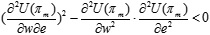 , U(πm) is the strict concave function of w and e, and by setting
, U(πm) is the strict concave function of w and e, and by setting 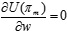 ,
, 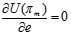 , we obtain the following optimal values,
, we obtain the following optimal values,
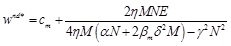 |
(7) |
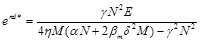 |
(8) |
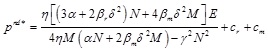 |
(9) |
Substituting Eq.(7)-(9) into Eq.(3) and (4), we have,
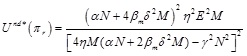 |
(10) |
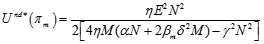 |
(11) |
Where M = α + βrδ2, N = α + 2βrδ2, E = K - αcm- αcr, K, is a large positive number that denotes the size of uncertain market demand, and α is a small positive number, then we have K - αcm- αcr > 0.
3.2. Centralized Decision Model
Under centralized decision-making, the manufacturer and retailer choose the wholesale price, carbon emission reduction level and retail price to maximize the utility of the supply chain system.
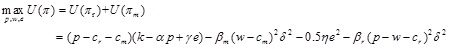 |
(12) |
When αη > γ, because 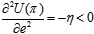 ,
, 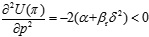 ,
, 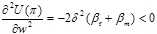 , by setting
, by setting 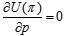 ,
, 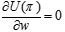 ,
, 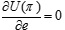 , we can obtain the optimal values pnc*, wnc*, enc* as follows,
, we can obtain the optimal values pnc*, wnc*, enc* as follows,
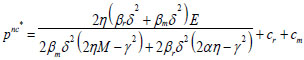 |
(13) |
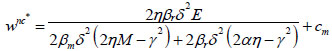 |
(14) |
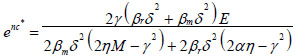 |
(15) |
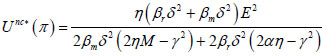 |
(16) |
Where M = α + βrδ2, E = K - αcm- αcr.
3.3. Comparative Analysis of the Results Under Decentralized and Centralized Decision-Making
Next, we compare and analyze the optimal results obtained by the decentralized and centralized decision models.
(1) When βr → 0, the retailer is risk neutral and the manufacturer is risk averse, the optimal results of the decentralized and centralized decision-making models are as follows.
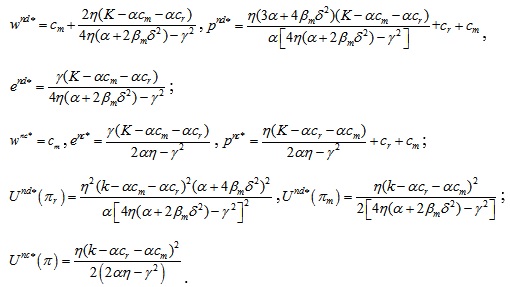
The following theorem 1 can be obtained from the comparison of the optimal pricing results.
Theorem 1: If the retailer is risk neutral and the manufacturer is risk averse, the relationships of the optimal prices under centralized and decentralized decision-making are as follows,
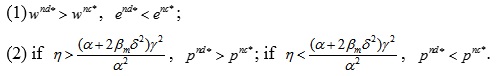
From theorem 1, it can be seen that when the manufacturer is risk averse, their optimal wholesale price in the decentralized decision model exceeds that under the centralized decision model, and the carbon emission reduction under the decentralized decision model is less than under the centralized decision model. That is, under the decentralized decision model, the manufacturer reduces the level of carbon emission reduction, and also improves the wholesale price. When the cost coefficient of carbon emission reduction is large, the retail price under the decentralized decision model exceeds that under the centralized decision model, while the retail price under the decentralized decision model is smaller when the cost coefficient of the carbon emission reduction is small. At this point, the decentralized supply chain system has lower utility than the centralized supply chain system.
By analyzing the relationship among optimal retail price, wholesale price and carbon emission reduction and manufacturer risk aversion coefficient, we can obtain inference 1, as follows:
Inference 1: 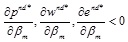
From inference 1, we can see that in the decentralized decision, the wholesale price, carbon emission reduction level and retail price all decrease with increased manufacturer risk aversion coefficient. This is because if the manufacturer is risk averse, they will reduce the carbon emission reduction level, reduce the wholesale price, and then wholesale the product to the retailer to reduce market demand uncertainty. The retailer's price will be reduced if their wholesale cost is reduced. In the centralized decision model, the wholesale price, carbon emission reduction level and retail price are independent of manufacturer risk aversion coefficient.
The relationship between the optimal retail price, wholesale price and carbon emission reduction level, and the carbon emission reduction cost coefficient and consumer low carbon preference coefficient can be described using inference 2, as follows:
Inference 2: 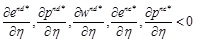 ;
; 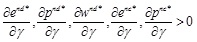
From inference 2, we can see that under the centralized and decentralized decision models, both carbon emission reduction and retail price decrease with the increase in the cost coefficient of carbon emission reduction, which increases with consumers' low carbon preference coefficient. Under the decentralized decision model the wholesale price also satisfies this relationship. Meanwhile, under the centralized decision model the wholesale price is independent of both the carbon emission reduction cost coefficient and the consumer low carbon preference coefficient. This is because the lower the carbon emission reduction cost coefficient, the greater the consumer low carbon preference coefficient, with the result that the manufacturer will increase both the carbon emission reduction level of the product, and also the retail and wholesale prices.
(2) When βm → 0, the manufacturer is neutral and the retailer is risk averse, and the optimal results of the decentralized and centralized decision models are as follows.
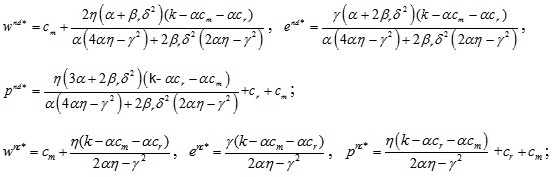
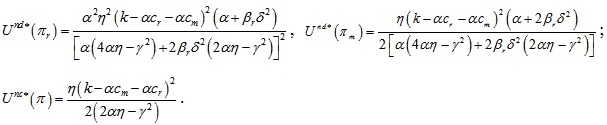
The following theorem 2 can be obtained from comparison of the optimal pricing results under the centralized and decentralized decision models.
Theorem 2: If the manufacturer is neutral and the retailer is risk averse, the relationships of the optimal prices under the centralized and decentralized decision models are: wnd* < wnc*, end* < enc*, pnd* > pnc*.
From theorem 2, we can see that the results when the retailer is risk averse differ from those when the manufacturer is risk averse (see Theorem 1). The wholesale price and carbon emission reduction level under the centralized decision model exceed those under the decentralized decision model, while the retail price under the decentralized decision model exceeds that under the centralized decision model. This is because, under the decentralized decision model, a risk averse retailer will set a higher retail price even if both carbon emission reductions and wholesale prices are low. At this point, the decentralized supply chain system has lower utility than the centralized supply chain system.
The relationship between the optimal retail price, the wholesale price and the carbon emission reduction level, and the carbon emission reduction cost coefficient and consumer low carbon preference coefficient can be described using inference 3, as follows:
Inference 3: 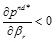 ,
, 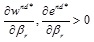
From inference 3 we can see that, under the decentralized decision model, when the retailer is risk averse, the wholesale price and carbon emission reduction level increase with the risk aversion coefficient of the retailer. This is because as the risk aversion coefficient of the retailer increases, the neutral manufacturer must increase product quality to attract retailers to order, which in turn increases carbon emission reductions and manufacturer profits. The carbon emission reduction cost of producing low carbon products will be transferred to the wholesale price. The wholesale price will increase as a result, and the retailer then reduces the retail price to avoid risk.
The relationship between the optimal retail price, the wholesale price and carbon emission reduction level, and the carbon emission reduction cost coefficient and consumer low carbon preference coefficient under the centralized and decentralized decision models can be described using inference 4, as follows:
Inference 4: 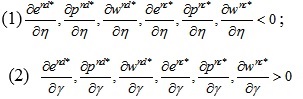
From inference 4, we can see that when the retailer is risk averse, under the decentralized and centralized decision models, the wholesale price, carbon emission reduction level and retail price are positively related to consumer low carbon preference level, and negatively related to the carbon emission reduction cost coefficient. When the consumer's low carbon preference level γ increases and the cost coefficient of carbon emission reduction is small, the manufacturer will increase their investment in carbon emission reduction and increase the wholesale price. The greater the carbon emission reduction level, the greater the carbon emission reduction cost, and this cost will be reflected in the higher retail prices.
(3) When βr → ∞, the retailer is completely risk averse, and the optimal results of the decentralized and centralized decision models are as follows.
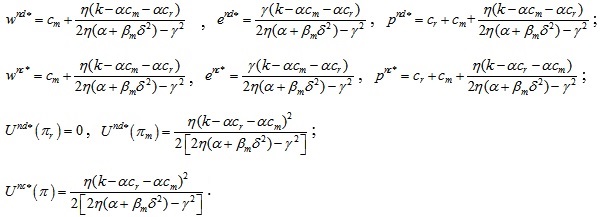
The following theorem 3 can be obtained from comparison of the optimal results under the centralized and decentralized decision models.
Theorem 3: If the retailer is completely risk averse, the relationships of the optimal results under the centralized and decentralized decision models are: wnd* = wnc*, end* = wnc*, pnd* = pnc*, Und*(πm) + Und*(πr) = Unc*(π).
From Theorem 3, we can see that, when the retailer is completely risk averse, the wholesale price, carbon emission reduction level and retail price under the decentralized decision model equal those under the centralized decision model. The total supply chain system utility under the decentralized decision model equals that under the centralized decision model. That is, when the retailer is completely risk averse, even in the absence of a contract, the decentralized decision model can achieve the same effect as the centralized decision model.
The relationship between the retail price, wholesale price and carbon emission reduction level and the manufacturer's risk aversion coefficient can be deduced using inference 5, as follows.
Inference 5: 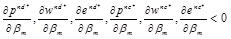
Like inference 1, the retail price, wholesale price and carbon emission reduction level under the centralized and decentralized decision models all decrease with the increase of the manufacturer's risk aversion coefficient. When manufacturer’s risk aversion coefficient is greater, the manufacturer will reduce the wholesale price and carbon emission reduction level, reduce income risk, and retailers will reduce retail prices accordingly.
The relationship between the optimal retail price, the wholesale price and the carbon emission reduction level, and the carbon emission reduction cost coefficient and consumer low carbon preference coefficient under the centralized and decentralized decision models is the same as when the retailer is risk averse and the manufacturer is risk neutral (see inference 4).
(4) When βm → ∞, the manufacturer is completely risk averse, and the optimal results obtained using the decentralized and centralized decision models are as follows.
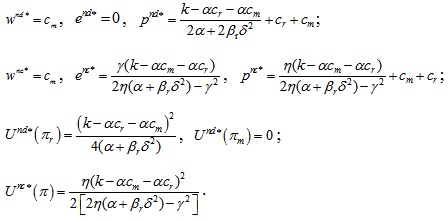
The following theorem 4 can be obtained by comparing the optimal results under the centralized and decentralized decision models.
Theorem 4: If the retailer is completely risk averse, the relationships of the optimal results under the centralized and decentralized decision models are: wnd* = wnc*, end* < enc*, pnd* < pnc*.
From theorem 4, we can see that the wholesale price under the decentralized decision model equals that under the centralized decision model. The level of carbon emission reduction and the retail price are both lower than under the centralized decision model. This is because, unlike when the manufacturer is risk averse, when the manufacturer is completely risk averse, under the decentralized decision model, the manufacturer reduces the carbon emission reduction level, reduces the wholesale price, and the retailer reduces the retail price accordingly. At this point, the utility of the decentralized supply chain is less than that under the centralized decision model.
When the manufacturer is completely risk averse, the relationship between retail price, wholesale price and carbon emission reduction level and manufacturer risk aversion coefficient can be deduced using inference 6, as follows:
Inference 6: 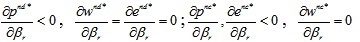
From inference 6, we can see that when the manufacturer is completely risk averse, under the decentralized decision model, the wholesale price and carbon emission reduction level are unrelated to the risk aversion coefficient of the retailer. The retail price is negatively related to the retailer’s risk aversion coefficient, and the retailer can increase efficiency by reducing the retail price. Under the centralized decision model, both the wholesale price and the retail price are independent of retailer’s risk aversion coefficient. Both the retail price and the carbon emission reduction level are negatively related to the risk aversion coefficient of the retailer. The greater the retailer's risk aversion coefficient, the more likely a completely risk averse manufacturer will reduce the investment in reducing the level of carbon emission while maintaining wholesale prices unchanged to reduce risk, with the result that retail prices will be reduced accordingly.
When the manufacturer is completely risk averse, by comparing the optimal carbon emission reduction level, retail price and wholesale price, we can find that, under the decentralized decision model, all three are independent of the carbon emission cost coefficient and the consumer low carbon preference coefficient, and the wholesale price under the centralized decision model is independent of the two coefficients. Under the centralized decision model, the relationship between the carbon emission reduction level, retail price and carbon emission reduction cost coefficient and consumer low carbon preference coefficient is summarized by inference 7, as follows:
Inference 7: 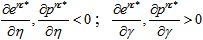
From inference 7, when the manufacturer is completely risk averse, under the centralized decision model, the level of carbon emission reduction and the retail price are positively related to consumer low carbon preference coefficient, and negatively related to the cost coefficient of carbon emission reduction.
4. LOW CARBON SUPPLY CHAIN SYSTEM COORDINATION BASED ON REVENUE SHARING CONTRACT
Only when the retailer is completely risk averse is the utility of the supply chain equal under the decentralized and centralized decision models. Under other conditions, the supply chain utility is low under the decentralized decision model. To effectively coordinate the operation efficiency of the supply chain system, the incentive mechanism of revenue sharing can be established to maximize the overall utility of the supply chain system. Suppose that a 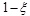 portion of the retailer's income will be transferred to the manufacturer. At this point, the utility functions of the manufacturer and retailer are as follows,
portion of the retailer's income will be transferred to the manufacturer. At this point, the utility functions of the manufacturer and retailer are as follows,
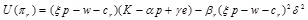
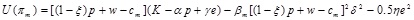
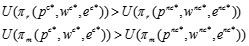 |
(17) |
Since 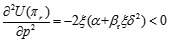 , by setting
, by setting 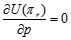 , the only optimal value pc* can be obtained as follows
, the only optimal value pc* can be obtained as follows
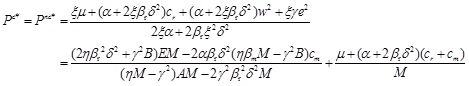 |
(18) |
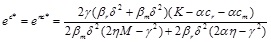 |
(19) |
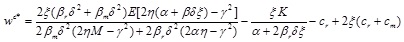 |
(20) |
Where M = α + βrδ2, E = K - αcr- αcm
Taking the condition of a risk averse manufacturer and risk neutral retailer as an example, when βr → 0, by substituting Eq.(19) into Eq.(18), we have,
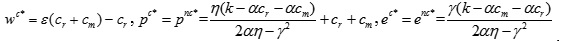
Since wnc* = cm, by substituting the above results into Eq.(17), we have,
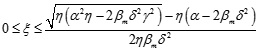 |
Where, α > 2βm δ2. That is, when the value interval of the ratio coefficient of income distribution is 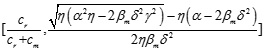 , the utility of the manufacturer and retailer can be optimized, and the supply chain can achieve perfect coordination.
, the utility of the manufacturer and retailer can be optimized, and the supply chain can achieve perfect coordination.
5. NUMERICAL SIMULATION ANALYSES RUNNING ON MATLAB
To more intuitively analyze the impact of parameters on the optimal decision results, a numerical simulation experiment is first performed running on Matlab, with a risk neutral retailer and a risk averse manufacturer. We assume βr = 0, K = 100, δ = 2, α = 0.25, cm = 40, cr = 20.
(1) When η = 0.5, γ = 0.2, under the decentralized and centralized decision models, the change in wholesale price, carbon emission reduction level, and retail price in the manufacturer’s risk aversion coefficient are described below in Fig. (1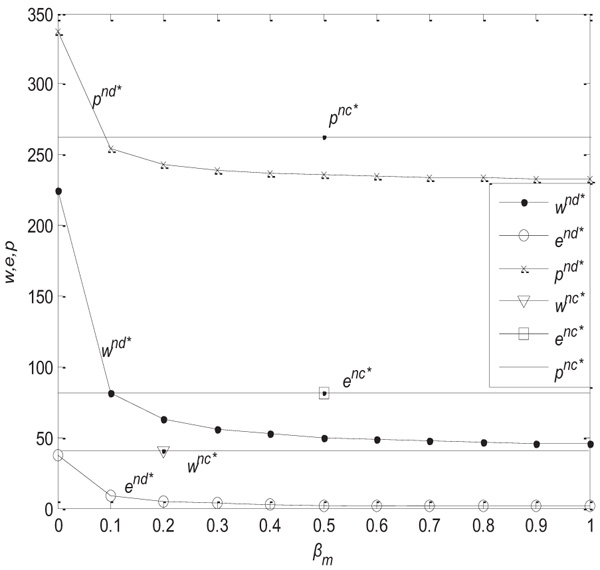 ).
).
As we can see from Fig. (1 ), when the manufacturer's risk aversion coefficient is small, the retail price under the decentralized decision model is higher than that under the centralized decision model. When the risk aversion coefficient of the manufacturer is large, the retail price under the decentralized decision model is less than that under the centralized decision model. The wholesale price under the decentralized decision model is higher than that under the centralized decision model. Meanwhile the carbon emission reduction under the decentralized decision model is lower than that under the centralized decision model.
), when the manufacturer's risk aversion coefficient is small, the retail price under the decentralized decision model is higher than that under the centralized decision model. When the risk aversion coefficient of the manufacturer is large, the retail price under the decentralized decision model is less than that under the centralized decision model. The wholesale price under the decentralized decision model is higher than that under the centralized decision model. Meanwhile the carbon emission reduction under the decentralized decision model is lower than that under the centralized decision model.
 |
Fig. (1) The influence of βm on w, e, p. |
(2) When η = 0.5 and βm = 0.01 under the decentralized and centralized decision models, the change in wholesale price, carbon emission reduction level, and retail price given the consumer low carbon preference coefficient is described below in Fig. (2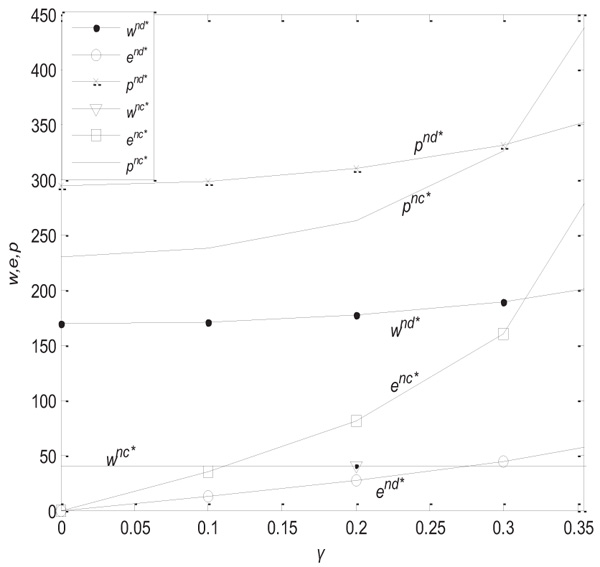 ).
).
From Fig. (2 ), we can see that, with the increase in consumer low carbon preference coefficient, when the manufacturer determines a higher carbon emission reduction level, the wholesale price will increase, and so too will the retail price set by the retailer. When the consumer low carbon preference coefficient is small, the retail price under the decentralized decision model exceeds that under the centralized decision model, and the retail price under the decentralized decision model is smaller than that under the centralized decision model when the consumer low carbon preference coefficient is large. The wholesale price under the decentralized decision model exceeds that under the centralized decision model. Meanwhile, the carbon emission reduction level under the decentralized decision model is lower than that under centralized decision model.
), we can see that, with the increase in consumer low carbon preference coefficient, when the manufacturer determines a higher carbon emission reduction level, the wholesale price will increase, and so too will the retail price set by the retailer. When the consumer low carbon preference coefficient is small, the retail price under the decentralized decision model exceeds that under the centralized decision model, and the retail price under the decentralized decision model is smaller than that under the centralized decision model when the consumer low carbon preference coefficient is large. The wholesale price under the decentralized decision model exceeds that under the centralized decision model. Meanwhile, the carbon emission reduction level under the decentralized decision model is lower than that under centralized decision model.
 |
Fig. (2) The influence of γ on w, e, p. |
(3) When γ = 0.2, βm = 0.01, under both the decentralized and centralized decision models, the change in wholesale price, carbon emission reduction level, retail price in the carbon emission reduction cost coefficient can be described in Fig. (3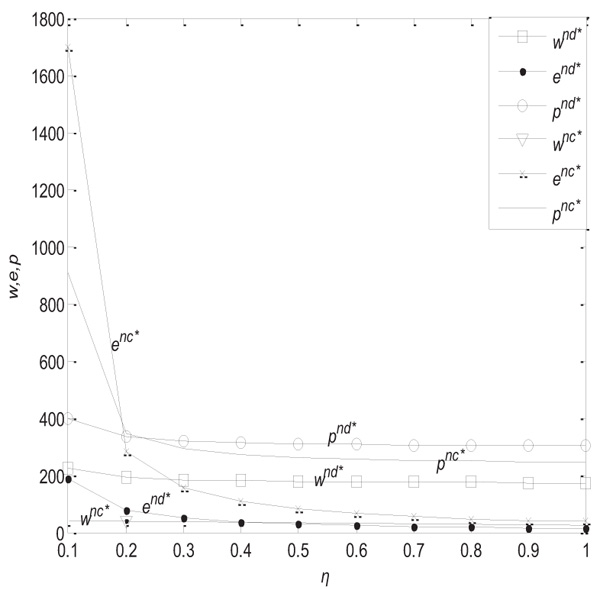 ) below.
) below.
 |
Fig. (3) The influence of η on w, e, p. |
From Fig. (3 ), we can see that, with the increase of the carbon emission reduction cost coefficient, the wholesale price decreases under the decentralized decision model, and the retail price and carbon emission reduction level decrease under both kinds of decision models. When the cost coefficient of carbon emission reduction is small, the retail price under the centralized decision model exceeds that under the decentralized decision model. When the cost coefficient of carbon emission reduction is large, the carbon emission reduction level under the centralized decision model exceeds that under the decentralized decision model. The wholesale price under the centralized decision model is lower than that under the decentralized decision model.
), we can see that, with the increase of the carbon emission reduction cost coefficient, the wholesale price decreases under the decentralized decision model, and the retail price and carbon emission reduction level decrease under both kinds of decision models. When the cost coefficient of carbon emission reduction is small, the retail price under the centralized decision model exceeds that under the decentralized decision model. When the cost coefficient of carbon emission reduction is large, the carbon emission reduction level under the centralized decision model exceeds that under the decentralized decision model. The wholesale price under the centralized decision model is lower than that under the decentralized decision model.
(4) When η = 0.5, γ = 0.2, before and after coordination, the ratio of income distribution 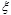 is 0.3, 0.4, 0.5, and the changes in the utility of the retailer and manufacturer with the manufacturer’s risk coefficient are as shown in Figs. (4
is 0.3, 0.4, 0.5, and the changes in the utility of the retailer and manufacturer with the manufacturer’s risk coefficient are as shown in Figs. (4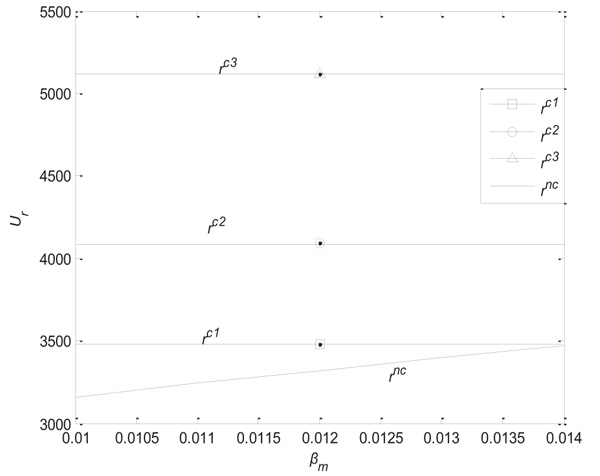 and 5
and 5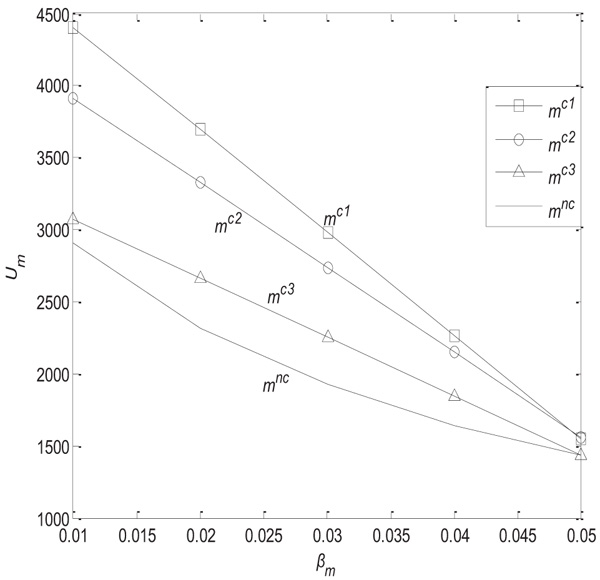 ).
).
As can be seen from Figs. (4 and 5
and 5 ), when the retailer is risk neutral and the profit sharing coefficient is fixed, the manufacturer's utility decreases with increasing manufacturer risk aversion coefficient, and the retailer's utility increases with increasing manufacturer risk aversion coefficient. Coordination increases the utilities of the manufacturer and retailer. The utility of the retailer is not related to the risk aversion factor of the manufacturer, or to the increase of the sharing coefficient of income. Given constant manufacturer risk aversion coefficient, the utility of the retailer is increasing, and that of the manufacturer is decreasing.
), when the retailer is risk neutral and the profit sharing coefficient is fixed, the manufacturer's utility decreases with increasing manufacturer risk aversion coefficient, and the retailer's utility increases with increasing manufacturer risk aversion coefficient. Coordination increases the utilities of the manufacturer and retailer. The utility of the retailer is not related to the risk aversion factor of the manufacturer, or to the increase of the sharing coefficient of income. Given constant manufacturer risk aversion coefficient, the utility of the retailer is increasing, and that of the manufacturer is decreasing.
 |
Fig. (4) The influence of βm on the retailer’s utility. |
 |
Fig. (5) The influence of βm on the manufacturer’s utility. |
(5) When η = 0.5, γ = 0.2, before and after coordination, the risk aversion coefficient of the manufacturer βm is set to 0.01, 0.02, 0.03, and the changes in the utility of the retailer and manufacturer with the income sharing coefficient 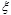 are shown below in Figs. (6
are shown below in Figs. (6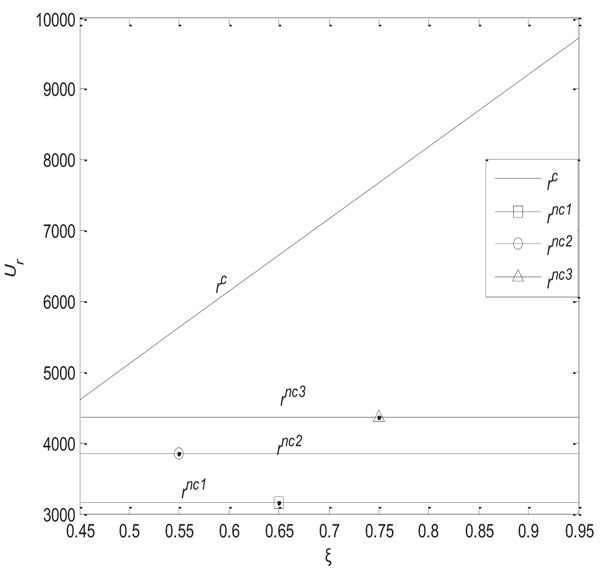 and 7
and 7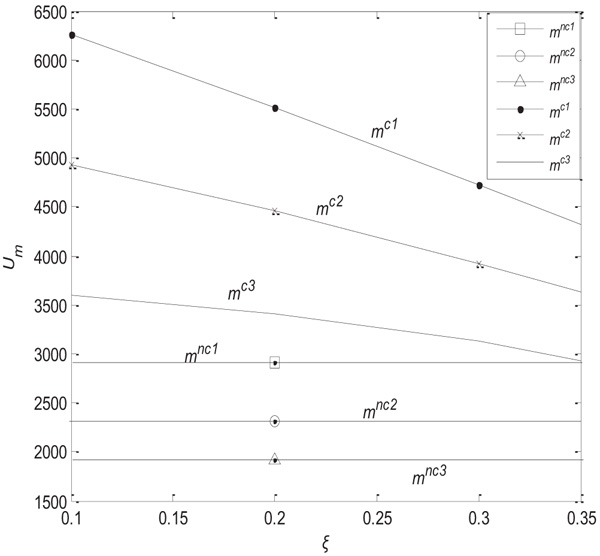 ).
).
As can be seen from Figs. (6 and 7
and 7 ), when the retailer is risk neutral and the manufacturer's risk aversion coefficient is fixed, the utilities of the manufacturer and retailer are greater than without such coordination. The utility of the retailer increases with increasing income share coefficient, and the manufacturer's utility decreases with increasing income sharing coefficient. As the risk aversion coefficient of the manufacturer increases, the utility decreases under the same income sharing coefficient.
), when the retailer is risk neutral and the manufacturer's risk aversion coefficient is fixed, the utilities of the manufacturer and retailer are greater than without such coordination. The utility of the retailer increases with increasing income share coefficient, and the manufacturer's utility decreases with increasing income sharing coefficient. As the risk aversion coefficient of the manufacturer increases, the utility decreases under the same income sharing coefficient.
 |
Fig. (6) The influence of 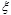 on the retailer’s utility. on the retailer’s utility.
|
 |
Fig. (7) The influence 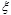 on the manufacturer’s utility. on the manufacturer’s utility.
|
CONCLUSION
In a two-level low carbon supply chain system consisting of a manufacturer and a retailer, the manufacturer first decides the wholesale price and carbon emission reduction level, and then the retailer decides the retail price, with both parties playing a Stackelberg game. Through comparative analysis of the decentralized and centralized decisions, the optimal decision problem of the manufacturer and retailer under different risk aversion models is investigated. Additionally, the influences of consumer low carbon preference coefficient and carbon emission cost coefficient on decision variables of manufacturers and retailers are researched. The results show that: (1) When the manufacturer is risk neutral and the retailer is risk averse, the wholesale price under the decentralized decision model will be less than that under the centralized decision model, given the low carbon preference and carbon emission reduction factor. (2) When the retailer is completely risk averse, the effect equals that under the centralized decision model without any coordination contract. (3) Under the scenario with different risk aversion coefficients, the consumer low carbon preference coefficient and carbon emission cost coefficient equally influence the decision variables of the manufacturer and the retailer, which are positively correlated with the low carbon preference coefficient and negatively correlated with the carbon emission reduction cost coefficient. (4) When the revenue sharing coefficient satisfies a certain range, the revenue sharing contract can perfectly coordinate the supply chain, which optimizes the utilities of the manufacturer and retailer. These results can help the manufacturer and the retailer make decisions under different risk aversion models. This paper considers the problem of low carbon supply chain system decision under information symmetry. The influences of information asymmetry, carbon trading and carbon tax on risk aversion in a low carbon supply chain system require further study.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGMENTS
The authors would like to thank the editor and the two anonymous referees for their constructive comments, which help to improve the original manuscript significantly. The authors also thank Seamus Harris, M.A., from Liwen Bianji, Edanz Editing China (www.liwenbianji.cn/ac), for editing the English text of a draft of this manuscript. This research was supported by the National Natural Science Foundation of China (Grant NO. 71771055) and the Key Projects of Excellent Youth Support Program in Universities (Grant NO. gxyqZD2018063).
REFERENCES
| [1] | J. Chen, "Study on supply chain management in a Low carbon era", J. Syst. Manage., vol. 21, no. 6, pp. 721-728. |
| [2] | Z.F. Mao, S. Zhang, and X.M. Li, "Low carbon supply chain firm integration and firm performance in China", J. Clean. Prod., vol. 153, no. 1, pp. 354-361. [http://dx.doi.org/10.1016/j.jclepro.2016.07.081] |
| [3] | Y.F. Zu, L.H. Chen, and Y. Fan, "Research on low-carbon strategies in supply chain with environmental regulations based on differential game", J. Clean. Prod., vol. 177, no. 10, pp. 527-546. [http://dx.doi.org/10.1016/j.jclepro.2017.12.220] |
| [4] | C.Q. Xu, D.Z. Zhao, and B.Y. Yuan, "Study on coordination mechanisms and differential pricing of supply chain in low carbon environment", Oper. Res. Manage. Sci., vol. 24, no. 1, pp. 19-26. |
| [5] | B.B. Cao, Z.D. Xiao, and C.Y. Zhu, "Study on supply chain decision under double sales model considering government low carbon policy", Chinese Journal of Management Science, vol. 26, no. 4, pp. 30-40. |
| [6] | Y Li, and D Z Zhao, "Low-carbonization supply chain coordination with contracts considering fairness preference", Journal of Industrial Engineering / Engineering Management, vol. 29, no. 1, pp. 156-161. |
| [7] | Q.P. Wang, D.Z. Zhao, and L.F. He, "Contracting emission reduction for supply chains considering market low-carbon preference", J. Clean. Prod., vol. 120, no. 1, pp. 72-84. [http://dx.doi.org/10.1016/j.jclepro.2015.11.049] |
| [8] | Q.P. Wang, and D.Z. Zhao, "Revenue-sharing contract of supply chain based on consumer’s preference for low carbon products", Chinese Journal of Management Science, vol. 22, no. 9, pp. 106-113. |
| [9] | J.N. Sun, and Z.D. Xiao, "Research on emission reduction strategy of low carbon supply chain considering consumer’s dual preferences", Chinese Journal of Management Science, vol. 26, no. 4, pp. 49-56. |
| [10] | L.H. Zhang, G.W. Zhang, and R. Zhang, "Equilibrium contracts strategies of low carbon supply chain and high carbon supply chain", Computer Integrated Manufacturing Systems, vol. 24, no. 3, pp. 763-771. |
| [11] | T.J. Xiao, T.M. Choi, D.Q. Yang, and T.C.E. Cheng, "Service commitment strategy and pricing decisions in retail supply chains with risk-averse players", Serv. Sci., vol. 4, no. 3, pp. 236-252. [http://dx.doi.org/10.1287/serv.1120.0021] |
| [12] | F. Ye, and Q. Lin, "Revenue sharing contract mechanisms of risk-averse supply chains", Journal of Industrial Engineering/ Engineering Management, vol. 26, no. 1, pp. 113-118. |
| [13] | J. Ning, V. Babich, J. Handley, and J. Keppo, "Risk-aversion and B2B contracting under asymmetric information: Evidence from managed print services", Oper. Res., vol. 66, no. 2, pp. 392-408. [http://dx.doi.org/10.1287/opre.2017.1673] |
| [14] | J.S. Dai, W.D. Meng, and B. Fan, "Supply chain coordination with risk aversion via buy-back contracts", Journal of Management Science in China, vol. 18, no. 5, pp. 57-65. |
| [15] | M.L. Xu, X.Z. Nie, and H.Y. Jian, "Pricing decision of dual-channel supply chain with risk preference", Control and Decision, vol. 31, no. 1, pp. 91-98. |
| [16] | M.Q. Liu, E. Cao, and K. Salifou, "Pricing strategies of a dual-channel supply chain with risk aversion", Transp. Res., Part E Logist. Trans. Rev., vol. 90, no. 6, pp. 108-120. [http://dx.doi.org/10.1016/j.tre.2015.11.007] |
| [17] | Y.W. Zhou, J.C. Li, and Y.G. Zhang, "Cooperative advertising and ordering policies in a two-echelon supply chain with risk-averse agents", Omega, vol. 75, no. 3, pp. 97-117. [http://dx.doi.org/10.1016/j.omega.2017.02.005] |
| [18] | B. Yan, Z.J. Jin, Y.P. Liu, and J.B. Yang, "Decision on risk-averse dual-channel supply chain under demand disruption", Commun. Nonlinear Sci. Numer. Simul., vol. 55, no. 2, pp. 206-224. [http://dx.doi.org/10.1016/j.cnsns.2017.07.003] |
| [19] | S.H. Yoo, "Product quality and return policy in a supply chain under risk aversion of a supplier", Int. J. Prod. Econ., vol. 154, no. 8, pp. 146-155. [http://dx.doi.org/10.1016/j.ijpe.2014.04.012] |
| [20] | L.L. Zhang, and Z. Yao, "Optimal strategy of risk-averse dual-channel supply chain with consumer returns", Computer Integrated Manufacturing Systems, vol. 21, no. 3, pp. 766-775. |
| [21] | X.G. Cao, B.R. Zheng, H.S. Xia, H. Wen, and J.Z. Li, "Analysis on closed-loop supply chain network equilibrium with risk-averse retailers", Control and Decision, vol. 29, no. 4, pp. 659-665. |
| [22] | J.S. Dai, and W.D. Meng, "Revenue sharing contract for a risk-averse supply chain with promotional effect", Journal of Management Science in China, vol. 17, no. 5, pp. 25-34. |
| [23] | X.H. Gan, and K.F. Ying, "Vendor managed inventory contract model with risk averse", Syst. Eng., vol. 33, no. 1, pp. 116-121. |
| [24] | C.T. Zhang, and L.P. Liu, "Research on coordination mechanism in three-level green supply chain under non-cooperative game", Appl. Math. Model., vol. 37, no. 5, pp. 3369-3379. [http://dx.doi.org/10.1016/j.apm.2012.08.006] |



