- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Cybernetics & Systemics Journal
(Discontinued)
ISSN: 1874-110X ― Volume 12, 2018
A Novel Arithmetic Technique for Generalized Interval-Valued Triangular Intuitionistic Fuzzy Numbers and Its Application in Decision Making
Palash Dutta*, Pranjal Talukdar
Abstract
Background:
Uncertainty is an integral part of decision-making process which arises due to the lack of knowledge, data or information. Initially Fuzzy Set Theory (FST) was used to handle this type of uncertainty. Later, Intuitionistic Fuzzy Set (IFS) was developed to encounter uncertainty in a more specific manner. However, it is observed that due to the existence of different types of uncertainties, the Membership Function (MF) of IFS itself is uncertain and consequently, the concept of Interval-Valued Intuitionistic Fuzzy sets (IVIFS) came into the picture. But IVIFS is also not capable of handling uncertainty. To overcome the limitations of the existing IVIFS, Generalized Interval Valued Intuitionistic Fuzzy Sets (GIVIFS) have been defined and it has been observed that it has utmost applicability in real world situations as the parameter height characterises the degree of buoyancy of judgment of decision maker in a very specific compartment.
Objective:
An arithmetic operation on GIVTIFNs is always a critical concern and the conventional way of performing arithmetic operations on GIVTIFNs has some shortcomings. This paper attempts to devise a novel technique to effectively resolve the drawbacks of conventional arithmetic operations on GIVTIFNs. Numerical examples are illustrated herewith and to justify the need of a new solution. Furthermore, an application of multi-criteria group decision-making problem was also carried out under this setting.
Method:
For the arithmetic operations on GIVTIFNs, the largest membership function is truncated at the minimum height first and the non-membership function is truncated at the maximum height. Accordingly, arithmetic operations on GIVTIFNs are defined. For this purpose, Decomposition theorems for GIVTrIFNs are discussed first.
Result:
The outputs are obtained as generalized interval-valued trapezoidal intuitionistic fuzzy numbers (GIVTrIFNs). The interesting part of the proposed approach is that it produces GIVTrIFNs. To check the validity and novelty of the approach, a multi criteria decision making was performed which obtained desirable results.
Conclusion:
The arithmetic GIVTIFNs conventional approach produces invariant output in the form of GIVTIFNs for GIVTIFNs of different height. But for the same input GIVTIFNs, the present approach provided different GIVTrIFNs. It was observed that the proposed approach is efficient, simple, logical, technically sound and general enough for implementation. Researchers may apply this approach in any field where GIVTIFNs are involved.
Article Information
Identifiers and Pagination:
Year: 2018Volume: 12
First Page: 72
Last Page: 120
Publisher Id: TOCSJ-12-72
DOI: 10.2174/1874110X01812010072
Article History:
Received Date: 30/3/2018Revision Received Date: 29/05/2018
Acceptance Date: 14/06/2018
Electronic publication date: 31/07/2018
Collection year: 2018
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: (https://creativecommons.org/licenses/by/4.0/legalcode). This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
* Address correspondence to this author at the Department of Mathematics, Dibrugarh University, Dibrugarh, Assam 786004, India; Tel: +919435184995; E-mail: palash.dtt@gmail.com
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 30-3-2018 |
Original Manuscript | A Novel Arithmetic Technique for Generalized Interval-Valued Triangular Intuitionistic Fuzzy Numbers and Its Application in Decision Making | |
1. INTRODUCTION
In the presence of different constraints in real life situation and due to highly complex environment, decision makers may provide their opinion under uncertain and imprecise nature. Due to the involvement of uncertainty crisp data are not always adequate to model in many real-life situations whereas FST introduced by L.A. Zadeh [1L.A. Zadeh, "Fuzzy sets", Inf. Control, vol. 8, pp. 338-356.
[http://dx.doi.org/10.1016/S0019-9958(65)90241-X] ], is more suitable and realistic to handle such type of situation. After the development of fuzzy set theory, further developments have been made by different researchers. Chen [2S.H. Chen, "Operations on fuzzy numbers with function principal", Tamkang J. Manage. Sci., vol. 6, pp. 13-26.] further developed the fuzzy set theory (fuzzy numbers) and named as Generalized Fuzzy Numbers (GFN) and performed all arithmetic operations between GFNs based on function principal. GFNs have been applied in different fields such as reliability analysis, risk analysis, pattern recognition, Rotor Fault Diagnosis, maximal flow problems, series-parallel system etc.
On the other hand, an important generalization of fuzzy set theory is the theory of Intuitionistic Fuzzy Set (IFS), introduced by Atanassov [3K.T. Atanassov, "Intuitionistic fuzzy sets", Fuzzy Sets Syst., vol. 20, pp. 87-96.
[http://dx.doi.org/10.1016/S0165-0114(86)80034-3] ] describing a membership degree and a non-membership degree separately in such a way that sum of the two degrees must not exceed to one. It is observed that fuzzy sets are IFSs but the converse is not necessarily correct. Further, Atanassov and Gargov [4K. Atanassov, and G. Gargov, "Interval valued intuitionistic fuzzy sets", Fuzzy Sets Syst., vol. 31, pp. 343-349.
[http://dx.doi.org/10.1016/0165-0114(89)90205-4] ] developed the notion of Interval-Valued Intuitionistic Fuzzy Sets (IVIFSs) in relation with interval-valued fuzzy sets and IFS. The IVIFSs are characterised by a membership function and a nonmembership function that take interval values rather than the exact number. In human cognitive and decision making processes, it is not absolutely justifiable or technically sound to represent the membership and nonmembership in terms of a single numeric value. Thus, IVIFSs have got more attention due to its ability to handle imprecise and unorganised information in terms of intervals instead of taking a single numeric value [5T.Y. Chen, "Interval valued intuitionistic fuzzy QUALIFLEX method with a likehood-based comparison approach for multiple criteria decision analysis", Inf. Sci., vol. 261, pp. 149-169.
[http://dx.doi.org/10.1016/j.ins.2013.08.054] ]. IFS and IVIFS have been successfully applied [6T. Rashid, I. Beg, and S.M. Husnine, "Robot selection by using generalized interval-valued fuzzy numbers with TOPSIS", Appl. Soft Comput. J., vol. 21, pp. 462-468. [http://dx.doi.org/10.1016/j.asoc.2014.04.002].
[http://dx.doi.org/10.1016/j.asoc.2014.04.002] -12K. Atanassov, G. Pasi, and R. Yager, "Intuitionistic fuzzy interpretations of multi-person multicriteria decision making", Proc. Of First Intern. IEEE Symposium Intell. Syst, vol. 1, pp. 115-119.
[http://dx.doi.org/10.1109/IS.2002.1044238] ] in different areas like decision making, pattern recognition, medical diagnosis. Yager, Yuan and Li [13X. Yuan, and H. Li, "Cut sets on interval-valued intuitionistic fuzzy sets", IEEE Sixth International Conference on Fuzzy Systems and Knowledge Discovery, FSDK, vol. 6, pp. 167-171.
[http://dx.doi.org/10.1109/FSKD.2009.606] -15R.R. Yager, "Some aspects of intuitionistic fuzzy sets", Fuzzy Optim. Decis. Making, vol. 8, pp. 67-90.
[http://dx.doi.org/10.1007/s10700-009-9052-7] ] studied the cut set characteristic of IVIFS. Following the work of Szmidt and Kacprzyk [16E. Szmidt, and J. Kacprzyk, "Dilemmas with distances between intuitionstic fuzzy sets: Straightforward approaches may not work", Studies in Computational Intelligence, vol. 109, pp. 415-430.], Xu and Qiansheng [17X. Zeishui, "On similarity measures of interval-valued intuitionistic fuzzy sets and their application to pattern recognitions", J. Southeast Univ., vol. 23, pp. 139-143. [English Edition].-19Z. Qiansheng, J. Shengyi, J. Baoguo, and L. Shihua, "Some information measures for interval-valued intuitionistic fuzzy sets", Inf. Sci., vol. 180, no. 12, pp. 5130-5145.] applied IVIFS to pattern recognition. Further Yingjie and Qiansheng [20Z. Qiansheng, Y. Haixiang, and Z. Zhenhua, "An interval-valued fuzzy reasoning approach based on weighted similarity measure", Adv. Mat. Res., pp. 143-144., 21S. Xiaoyong, L. Yingjie, H. Jixue, and S. Zhaohui, "Description and reasoning method of uncertain temporal knowledge based on IFTPN", Control Decis., vol. 25, no. 10, pp. 1457-1462.] studied the interval-valued intuitionistic fuzzy reasoning. Xu and Li [22X. Zeshui, and R.R. Yager, "Intuitionistic and interval-valued intuitionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group", Fuzzy Optim. Decis. Making, vol. 8, pp. 123-139.
[http://dx.doi.org/10.1007/s10700-009-9056-3] -24L. Dengfeng, "Mathematical-Programming approach to matrix games with payoffs represented by Atanassov’s Interval- valued intuitionistic fuzzy sets", IEEE Trans. Fuzzy Syst., vol. 18, no. 6, pp. 1112-1128.
[http://dx.doi.org/10.1109/TFUZZ.2010.2065812] ], successfully carried IVIFS to decision making problems. The Generalized Intuitionistic Fuzzy Sets (GIFSs) were proposed by Mondal and Samanta [25T.K. Mondal, and S.K. Samanta, "Generalized intuitionistic fuzzy sets", Journal of Fuzzy Mathematics, vol. 10, pp. 839-861.] under the constraint that the minimum of the two degrees does not exceed half. Shu et al. [26M.H. Shu, C.H. Cheng, and J.R. Chang, "Using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly", Microelectron. Reliab., vol. 46, no. 12, pp. 2139-2148.
[http://dx.doi.org/10.1016/j.microrel.2006.01.007] ], first introduced the concept of Generalized Intuitionistic Fuzzy Numbers (GIFNs) and defined arithmetic operations between them. But later, it was found that there are some errors and misprints in the definition of the four arithmetic operations and those errors were conducted by Li [27L. Dengfeng, "A note on using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly", Microelectron. Reliab., vol. 48, p. 1741.
[http://dx.doi.org/10.1016/j.microrel.2008.07.059] ]. Zhenhua et al. [28Z. Zhenhua, Y. Jingyu, Y. Youpei, and Z. Qiansheng, "A Generalized Interval Valued Intuitionistic Fuzzy Sets theory", Advanced in Control Engineering and Information Science, vol. 15, pp. 2037-2041.] introduced the construction method of the Generalized Interval-Valued Intuitionistic Fuzzy Sets with Parameters (GIVIFSP), and defined complement operation, intersection operation and union operation on GIVIFS. Furthermore, they proved that like IFS and IVIFS, GIVIFS is a closed algebraic system for all these operations. Bhowmik et al. [29M. Bhowmik, "Some results on Generalized Interval valued Intuitionistic Fuzzy sets", Int. J. Fuzzy Syst., vol. 14, no. 2, .], Zhi et al. [30P.E.I. Zhi, L.U. Jian-Sha, and Z.H.E.N.G. Li, "Generalized Interval valuedIntuitionistic Fuzzy Numbers with Application in Workstation Assessment", System Engineering Theory & practice, vol. 32, no. 10, pp. 2198-2206.], and Adak et al. [31A.K. Adak, M. Bhowmik, and M. Pal, Decomposition Theorem of Generalized Interval valued Intuitionistic Fuzzy Sets., Contemporary Advancement in Information Technology Development in Dynamic Environment, . [DOI: 10.4018/978-1-4666-6252-0.ch009]
[http://dx.doi.org/10.4018/978-1-4666-6252-0.ch009] ] also studied different concepts of GIVIFSs. Baloui and Nadarajah [32E. Baloui Jamkhaneh, and S. Nadarajah, "A New generalized intuitionistic fuzzy sets", Hacet. J. Math. Stat., vol. 44, no. 6, pp. 1537-1551.] extended the IFSs to the concept of GIFSs and introduced some operators on GIFSs. Based on GIFSs, Shabani and Baloui [33A. Shabani, and E. Baloui Jamkhaneh, "A new generalized intuitionistic fuzzy numbers", J. Fuzzy Set Valued Anal., vol. 4, pp. 1-10.
[http://dx.doi.org/10.5899/2014/jfsva-00199] ] introduced GIFNs. Baloui [34E. Baloui Jamkhaneh, "New generalized interval valued intuitionistic fuzzy sets", Res. Commun. Math. Math. Sci., vol. 5, no. 1, pp. 33-46.] considered a new GIVIFSs and introduced some operators on GIVIFSs. He studied different basic operations like union, intersection, subset complement etc. and also transformed the operations on IVIFSs for the GIVIFSs.
This paper presents a novel efficient approach to perform arithmetic operations on GIVTIFNs using cut method. This approach effectively resolves the shortcomings of the existing approach. Numerical examples are illustrated. Also, to show the proper justification, validity, efficiency and applicability of the proposed approach, a multi-criteria group decision-making problem was carried out. The detail work has been compressed as follows. Section 2 starts with some relevant preliminary definitions. In section 3, decomposition theorems are discussed by using GIVTrIFNs. Section 4 presents the proposed approach of arithmetic operations of GIVTIFNs for different heights and the positivity of the proposed method in comparison to the earlier methods. Numerical examples are shown in section 5. Section 6 discusses the ranking of GIVTrIFNs. A multi-criteria decision-making problem is discussed by using the proposed arithmetic operations in section 7. Finally, a concrete conclusion has been drawn in section 8.
1.1. Drawback of Existing Approach and Motivation
In this section, we perform all the conventional basic arithmetic operations on GIVTIFNs. However, the problem can be seen in the arithmetic on GIVTIFNs due to different heights.
Considering two Generalized Interval-Valued Triangular Intuitionistic Fuzzy Numbers (GIVTIFNs) 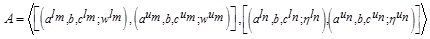 and
and 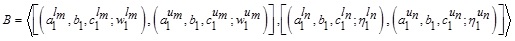 , the arithmetic operations are as follows:
, the arithmetic operations are as follows:
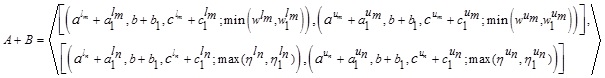 |
 |
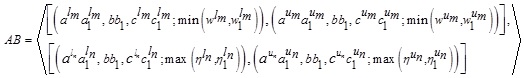 |
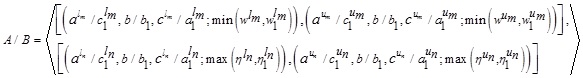 |
But this approach has some drawbacks and gives illogical results as during the operation, first it reduces the height of their respective (LMF and UMF) higher MFs to the height of the lower ones (i.e., make it as GIVTFN by reducing the height based on Cheng’s [26M.H. Shu, C.H. Cheng, and J.R. Chang, "Using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly", Microelectron. Reliab., vol. 46, no. 12, pp. 2139-2148.
[http://dx.doi.org/10.1016/j.microrel.2006.01.007] ] function principle) and similarly for the respective (LNMF and UNMF) NMFs, it increases the minimum height to maximum one to make it a generalized interval-valued triangular non-membership function. Therefore, this approach produces GIVTIFN with MF at the minimum height of the given respective (LMF and UMF) MFs of the GIVTIFNs and height of the NMF is maximum of the given respective (LNMF and UNMF) NMFs of GIVTIFNs to perform the arithmetic operations. The major drawback of this approach is that when performing arithmetic operations between a fixed GIVTIFN with different GIVTIFNs with the same support but different heights, the height of MFs of the fixed GIVTIFN is lesser and the height of NMFs is higher than other GIVTIFNs; then it is seen that each time, the resultant GIVTIFN remains invariant, which is illogical. For example consider 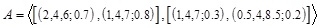 be a fixed GIVTIFN and
be a fixed GIVTIFN and 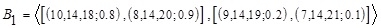 &
& 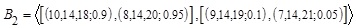 be two different GIVTIFNs with different heights. Then performing A*Bi (i=1,2), where * is the basic arithmetic operation using the existing approach to provide the same GIVTIFN. That is, the conventional approach gives
be two different GIVTIFNs with different heights. Then performing A*Bi (i=1,2), where * is the basic arithmetic operation using the existing approach to provide the same GIVTIFN. That is, the conventional approach gives
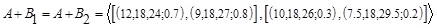 , which is clearly illogical as and are two different GIVTIFNs and the sum of these two GIVTIFNs with the fixed GIVTIFN A is identical. The following Figs. (1
, which is clearly illogical as and are two different GIVTIFNs and the sum of these two GIVTIFNs with the fixed GIVTIFN A is identical. The following Figs. (1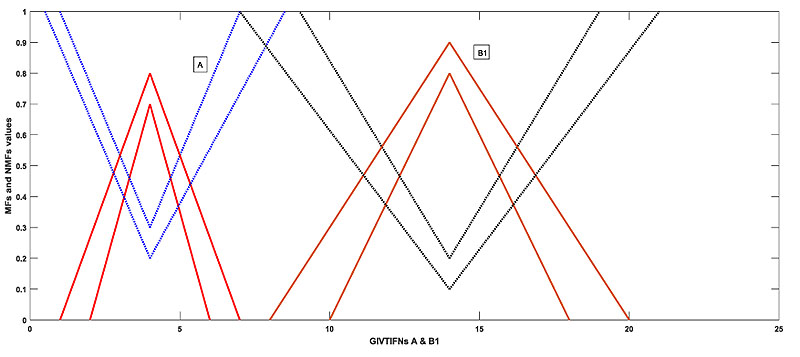 , 2
, 2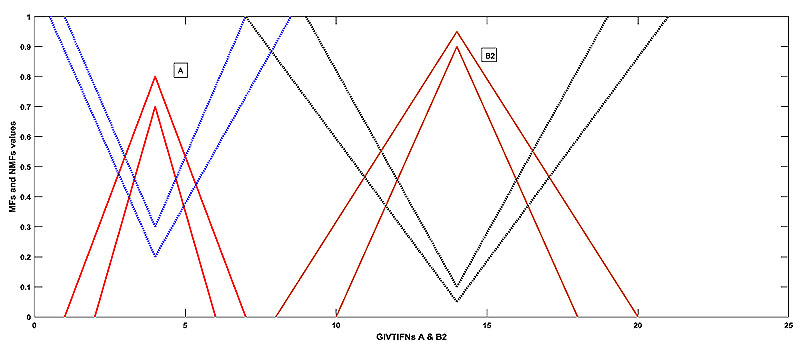 and 3
and 3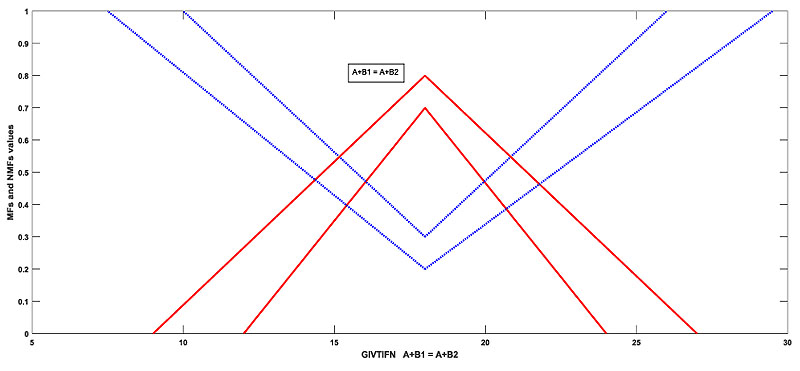 ) represent the above example.
) represent the above example.
 |
Fig. (1) A and B1. |
 |
Fig. (2) A and B2. |
 |
Fig. (3) Sum of GIVTIFNs. |
1.2. Motivation
GIVTIFNs play an important role while dealing with uncertainty modeling problems in real life situations as they have the capability to represent imprecision, uncertainty in a proper manner, and are desirable to address such problems. GIVTIFNs are used as mathematical assessment for different linguistic variables, ratings, and weights in various problems like decision making, medical diagnosis, pattern recognition etc. Proper arithmetic operations on GIVTIFNs are very important for the correct output in different problems. The existing approach produces some illogical results while performing arithmetic operation on GIVTIFNs with different heights. To overcome the shortcomings of the existing approach and for proper evaluation, it is always useful to define novel techniques for arithmetic on GIVTIFNs.
2. PRELIMINARIES
In this section, some basic definitions of FS, IFS and IVIFS have been discussed.
2.1. Definition (Fuzzy Set)
Let X be a universe of discourse; then the fuzzy subset A of X is defined by its membership function
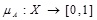 |
which assigns a real number µA (x) in the interval [0, 1], to each element 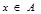 , where the value of µA (x) at x shows the grade of membership of x in A.
, where the value of µA (x) at x shows the grade of membership of x in A.
2.2. Definition
Given a fuzzy set A in X and any real number α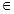 [0, 1]. Then,
[0, 1]. Then,
(a) (α-cut) the α -cut fuzzy set A, denoted by αA is the crisp set:
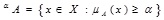 |
(b) (Strong a- cut) the strong a -cut, denoted by α+A is the crisp set:
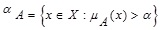 |
2.3. Definition (Support)
The support of a fuzzy set A defined on X is a crisp set defined as:
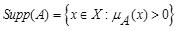 |
2.4. Definition (Height)
[1L.A. Zadeh, "Fuzzy sets", Inf. Control, vol. 8, pp. 338-356.
[http://dx.doi.org/10.1016/S0019-9958(65)90241-X] ] The height of a fuzzy set A, denoted by h(A), is the largest membership grade obtained by any element in the set and it is denoted as 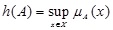 .
.
2.5. Definition (Generalized Fuzzy Numbers (GFN))
The membership function of GFN A= [a,b,c,d;w] where a ≤ b ≤ c ≤ d, 0 < w ≤ 1 is defined as:
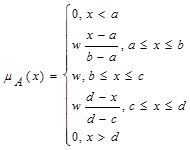 |
If w = 1, then GFN A is a normal trapezoidal fuzzy number A = [a, b, c, d]. If a = b and c = d, then A is a crisp interval.If b = c then A is a generalized triangular fuzzy number. If a = b = c = d and w = 1 then A is a real number. Compared to normal fuzzy number, the GFN can deal with uncertain information in a more flexible manner because of the parameter w that represents the degree of confidence of opinions of decision maker’s.
2.6. Definition (Intuitionistic Fuzzy Set (IFS))
An Intuitionistic fuzzy set A on a universe of discourse X is of the form:
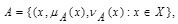 |
Where 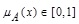 is called the “degree of membership of x in A”,
is called the “degree of membership of x in A”, 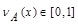 is called the “degree of non-membership of x in A”, and where µA(x) and vA(x) satisfy the following condition:
is called the “degree of non-membership of x in A”, and where µA(x) and vA(x) satisfy the following condition:
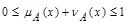 |
The amount πA(x) = 1 - (µA(x) + vA(x)) is called hesitancy of x which is a reflection of lack of commitment or uncertainty associated with the membership or non-membership or both in A.
2.7. Definition (Generalized Triangular Intuitionistic Fuzzy Number (GTIFN))
The membership function of GTIFN 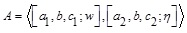 , where
, where 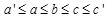 is defined as:
is defined as:
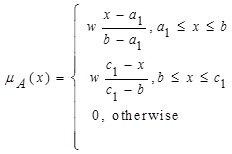 |
and the non-membership function of the GTIFS A is defined as:
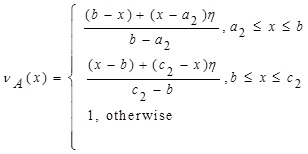 |
For example, consider the GTIFS 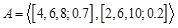 . The MF and NMF of A are shown in Fig. (4
. The MF and NMF of A are shown in Fig. (4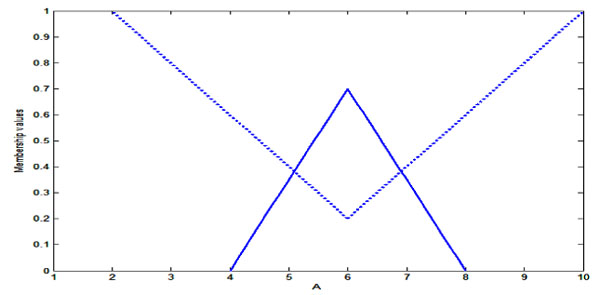 ).
).
 |
Fig. (4) Membership and non-membership of GTIFS 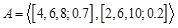 . .
|
2.8. Definition (Generalized Trapezoidal Intuitionistic Fuzzy Number (GTrIFN))
The membership function of trapezoidal GTrIFN 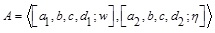 , where
, where 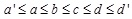 is defined as:
is defined as:
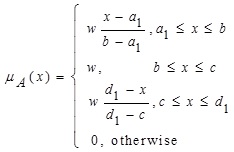 |
and the non-membership function of the GTrIFN A is defined as:
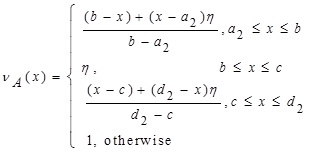 |
For example, consider the GTrIFS 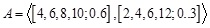 . The MF and NMF of A are shown in Fig. (5
. The MF and NMF of A are shown in Fig. (5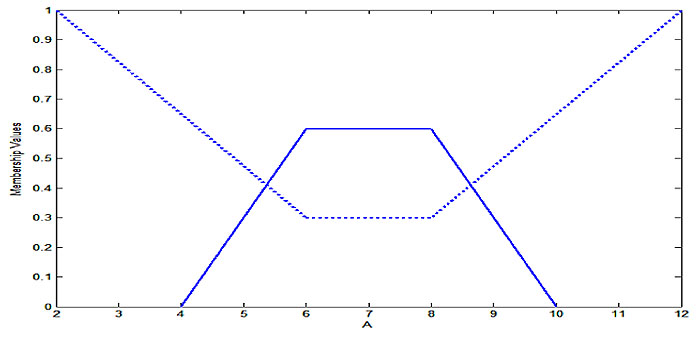 ).
).
 |
Fig. (5) Membership and non-membership of GTrIFS 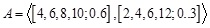 . .
|
2.9. Definition (Positive and Negative GIFS)
A GIFS is said to be positive GIFS a2 > 0 if and negative GIFS if a2 < 0.
2.10. Definition (Support of a GIFS)
Let
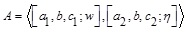 be a GIFS then support of A is defined as:
be a GIFS then support of A is defined as:
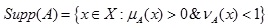
2.11. Definition (Height of a GFIS)
Let
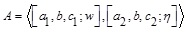 be a GIFS then height for MF is defined as:
be a GIFS then height for MF is defined as:
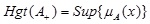 and height for NMF is defined as
and height for NMF is defined as 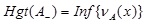 .
.
2.12. Definition (Level Set of GFIS)
Let
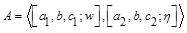 be a GIFS then level set for MF is defined as
be a GIFS then level set for MF is defined as 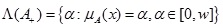
and level set for NMF is defined as 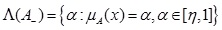
2.13. Definition (The α -cut of MF and NMF of the GIFS)
The α -cut of the MF of the GIFS 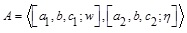 is defined as:
is defined as:
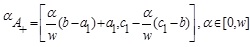
The α -cut of the NMF of the GIFS 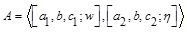 is defined as:
is defined as:
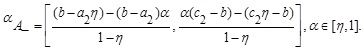
2.14. Definition ( The α -cut GIFS)
Let 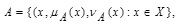 , be a GIFS and –-cut of MF (µA) be
, be a GIFS and –-cut of MF (µA) be 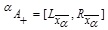 and NMF (vA) be
and NMF (vA) be 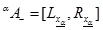 respectively. Then –-cut of GIFS A can be evaluated by the following formula:
respectively. Then –-cut of GIFS A can be evaluated by the following formula:
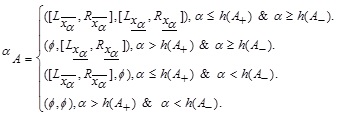 |
where 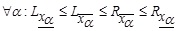 , A+ & A- mF and NMF such that
, A+ & A- mF and NMF such that 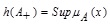 is the height of MF,
is the height of MF, 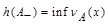 is the height of NMF and Ø is an empty set.
is the height of NMF and Ø is an empty set.
2.15. Definition (Special IFS)
Let 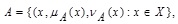 , be a GIFS defined on the universe of discourse X, then a special IFS can be defined as αA = α.αA.
, be a GIFS defined on the universe of discourse X, then a special IFS can be defined as αA = α.αA.
In particular, for MF αA+ = α.αA+, and for NMF, αA- = α.αA-.
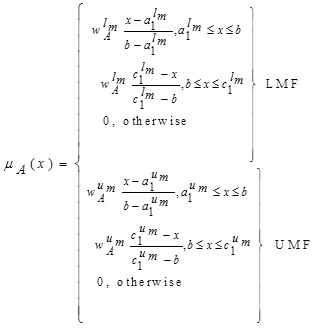
2.16. Definition (Generalized Interval-Valued Triangular Intuitionistic Fuzzy Number (GIVTIFN))
The membership functions (lower MF (LMF) and upper MF (UMF) of GIVTIFN
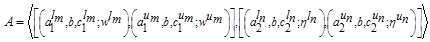 ,
,
where 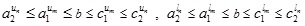 is defined as:
is defined as:
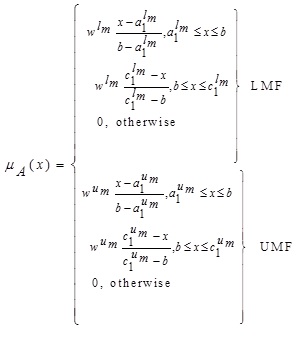 |
and the non-membership function of the GIVTIFN A is defined as:
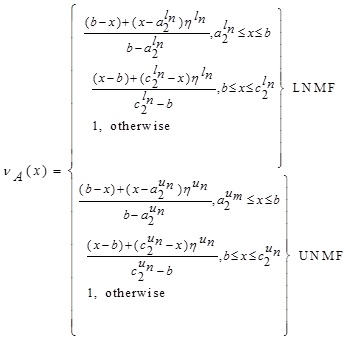 |
For example, consider the GIVTIFN 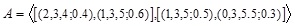 . The MFs and NMFs of A are shown in Fig. (6
. The MFs and NMFs of A are shown in Fig. (6 ).
).
 |
Fig. (6) MFs and NMFs of the GIVTIFNs 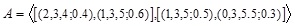 . .
|
2.17. Definition (Generalized Interval-Valued Trapezoidal Intuitionistic Fuzzy Number (GIVTrIFN))
The membership functions (LMF and UMF) of GIVTrIFN 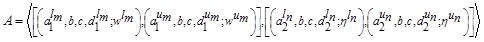 , where
, where 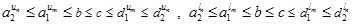 are defined as:
are defined as:
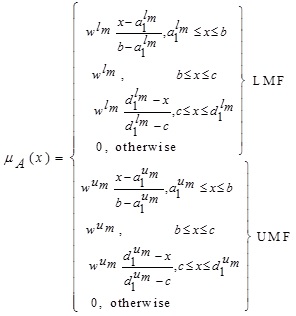 |
and the non-membership functions (lower NMF (LNMF) and upper NMF (UNMF)) of the GIVTrIFN A are defined as:
 |
For example, consider the GIVTrIFN 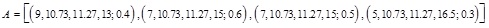 . The MFs and NMFs are shown in Fig. (7
. The MFs and NMFs are shown in Fig. (7 ).
).
 |
Fig. (7) MFs and NMFs of the GIVTrIFN 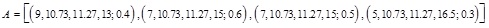 . .
|
2.18. Definition (Support of a GIVTIFS)
Let
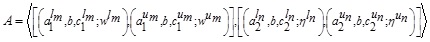 be a, GIVTIFS then support of A is defined as:
be a, GIVTIFS then support of A is defined as:
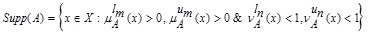 .
.
2.19. Definition (Height of a GIVTIFS)
Let
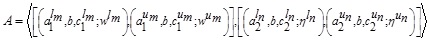 be a GIVTIFS, then height for MFs is defined as:
be a GIVTIFS, then height for MFs is defined as:
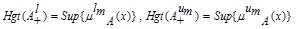 and height for NMFs are defined as
and height for NMFs are defined as 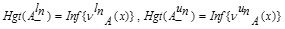 .
.
2.20. Definition (Level Set of GIVTIFS)
Let
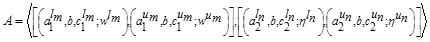 be a GIVTIFS, then the level set for MF is defined as:
be a GIVTIFS, then the level set for MF is defined as:
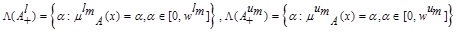 and level set for NMFs are defined as
and level set for NMFs are defined as
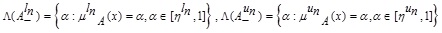 |
2.21. Definition (The α -cut of MFs and β -cut of NMFs of the GIVTIFS))
The α -cut of the MFs of the GIVTIFS 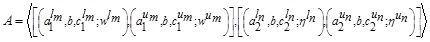 is defined as
is defined as
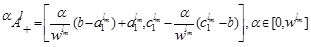
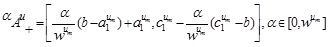
The α -cut of the NMFs of the GIVTIFS 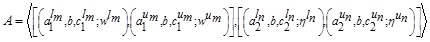 is defined as
is defined as
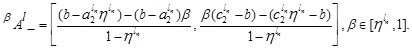
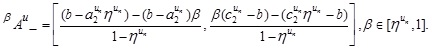
2.22. Definition (The α, β -cut GIVTIFS)
Let 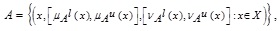 be a GIVTIFS and α-cut of MFs
be a GIVTIFS and α-cut of MFs 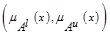 be
be 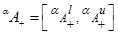 , where
, where 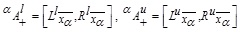 and NMFs
and NMFs 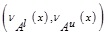 be
be 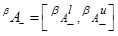 , where
, where 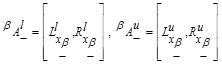 respectively. Then α,β-cut of GIVTIFS A can be evaluated by the following formula:
respectively. Then α,β-cut of GIVTIFS A can be evaluated by the following formula:
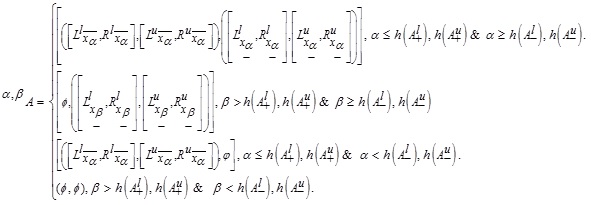
where 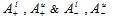 MFs and NMFs such that
MFs and NMFs such that 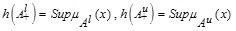 are the height of MFs,
are the height of MFs, 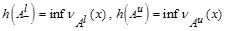 are the height of NMFs and is an empty set.
are the height of NMFs and is an empty set.
3. DECOMPOSITION THEOREM FOR GIVTrIFN
In this section, decomposition theorems for GIVTrIFN have been discussed.
3.1. Theorem (First Decomposition Theorem)
Let X be a universe of discourse. For any GIVTrIFN 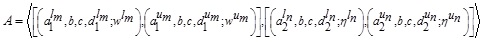 in X,
in X,
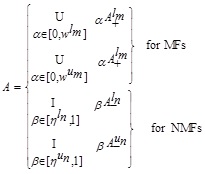
where 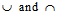 are standard fuzzy union and intersection, respectively.
are standard fuzzy union and intersection, respectively.
3.1.1. Proof
For MF, let for each 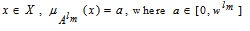 which indicates the degree of belonging in A.
which indicates the degree of belonging in A.
Then,
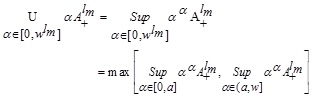 |
(3.1) |
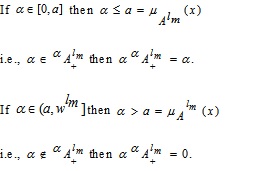
Hence from (3.1), we have
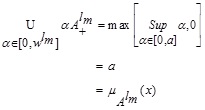
Similarly, 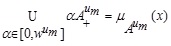
For NMF, let for each 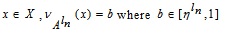 which indicates the degree of non-belonging in A.
which indicates the degree of non-belonging in A.
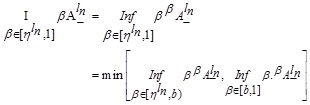 |
(3.2) |
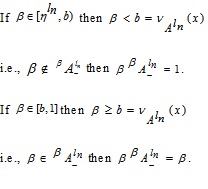
Hence from (3.2), we have
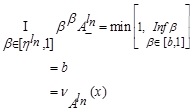
Similarly, 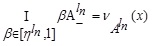 .
.
3.2. Theorem (Second Decomposition Theorem)
Let X be a universe of discourse. For any GIVTrIFN 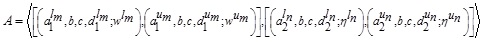 in X,
in X,
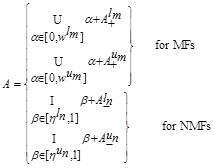
where 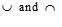 are standard fuzzy union and intersection, respectively.
are standard fuzzy union and intersection, respectively.
3.2.2. Proof
For MF, let for each 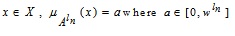 which indicates the degree of belonging in A.
which indicates the degree of belonging in A.
Then,
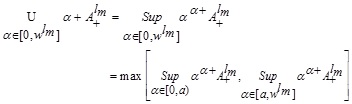 |
(3.3) |
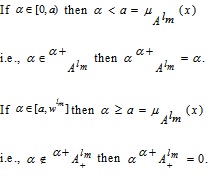
Hence from (3.3), we have
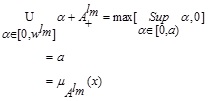
Similarly, 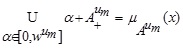
For NMF, let for each 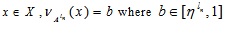 which indicates the degree of non-belonging in A.
which indicates the degree of non-belonging in A.
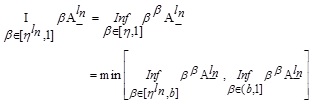 |
(3.4) |
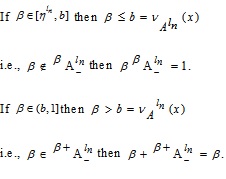
Hence from (3.4), we have
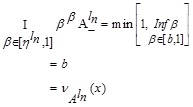
3.3. Theorem (Third Decomposition Theorem)
Let X be a universe of discourse. For any GIVTrIFN 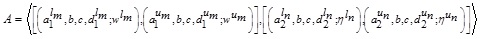 in X,
in X,
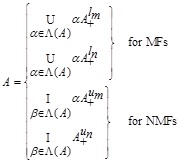
where 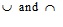 are standard fuzzy union and intersection, respectively, and λ(A) is the level set of A.
are standard fuzzy union and intersection, respectively, and λ(A) is the level set of A.
4. PROPOSED ARITHMETIC TECHNIQUE FOR GIVTIFNS
GIVTIFN is the extended version of GTIFN. Arithmetic on GIVTIFNs is a crucial issue. Let us consider that and are two GIVTIFNs with different heights. Here a novel approach will be discoursed to perform the arithmetic operation between GIVTIFNs A and B. In this approach, the MFs are truncated at the smallest height of their respective (LMF and UMF) MFs. Similarly, the NMFs are truncated at the maximum heights of their respective (LNMF and UNMF) NMFs. The interesting part of this approach is that it produces GIVTrIFNs.
Supposing that the MFs and NMFs of two GIVTIFNs 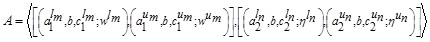 and
and 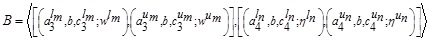 are:
are:
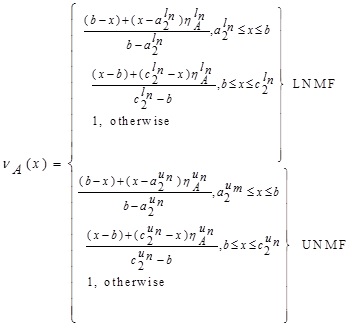
and
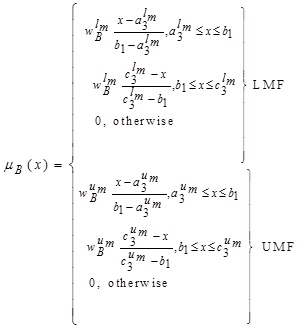
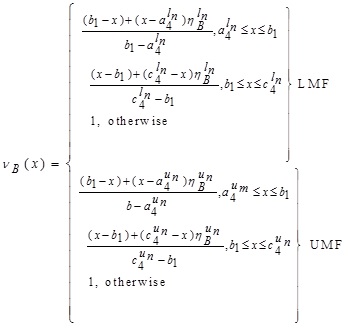
respectively.
then, the α, β-cut of A are 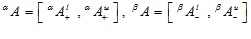 where
where
On the other hand, the α, βcut of B are  where
where
4.1. Theorem (Addition of Two GIVTIFNs with Different Heights Produces a GIVTrIFNs)
4.1.1. Proof
To determine the addition of GIVTIFNs A and B, we first add the α, βcuts of GITVIFNs A and B using interval arithmetic.
For MFs functions
 where
where 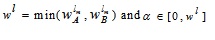 .
.
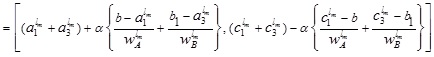 |
(4.1) |
To find the LMF 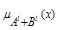 we equate both the first and second component of (4.1) to x which gives
we equate both the first and second component of (4.1) to x which gives
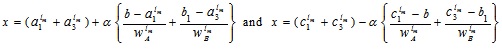
Now, expressing α in terms of x
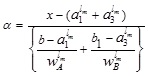 |
(4.2) |
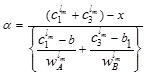 |
(4.3) |
Setting 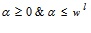 in (4.2) and
in (4.2) and 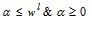 in (4.3), we get the domain of x,
in (4.3), we get the domain of x,
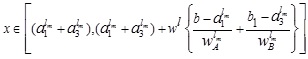 and
and 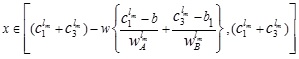
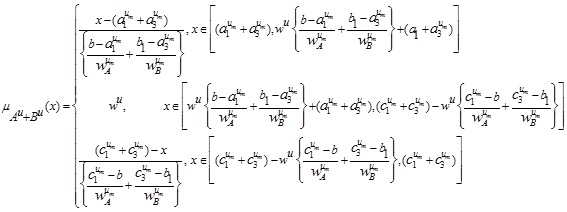
Hence the LMF 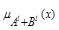 of is
of is
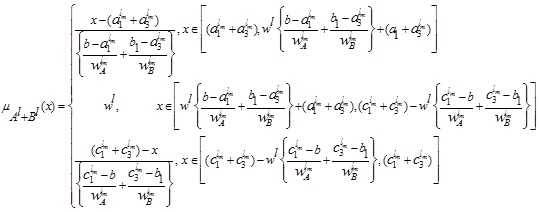
In a similar manner we also have the UMF 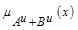 of A + B as
of A + B as
To obtain NMFs, we proceed as:
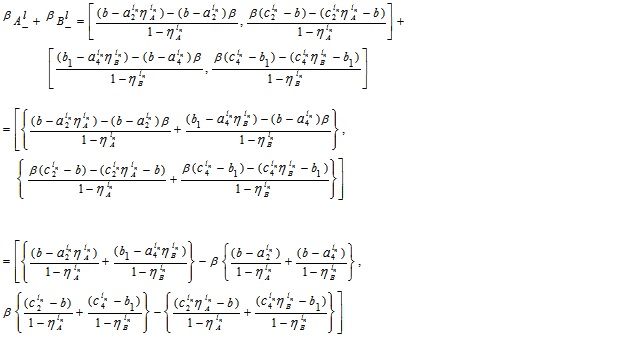
Let‘s equate each component with x, we have
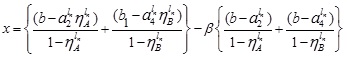 and
and 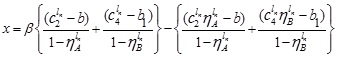
Now, expressing in terms of x, we obtain
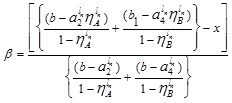 |
(4.4) |
and
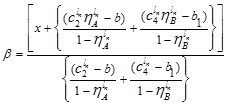 |
(4.5) |
Putting 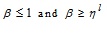 in (4.4), where
in (4.4), where 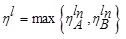 , we have
, we have
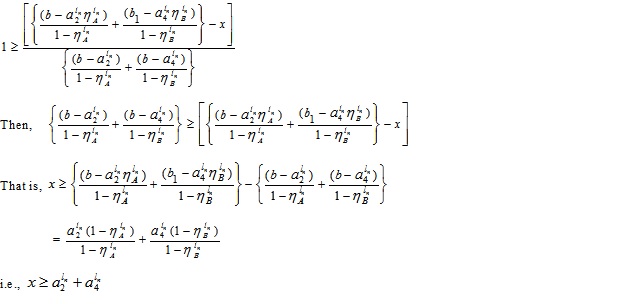
Again, taking 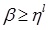 in (4.4), we have
in (4.4), we have
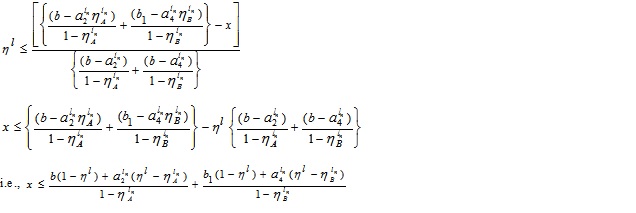
That is, 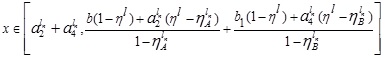 for (4.4)
for (4.4)
Next, Putting 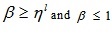 in (4.5), we have
in (4.5), we have
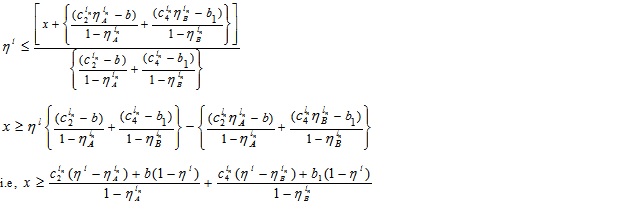
Again for, 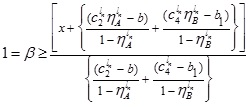
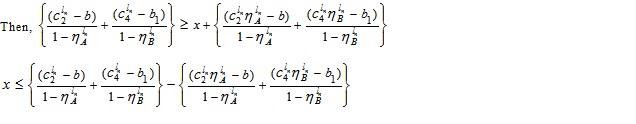
i.e., 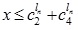
That is, 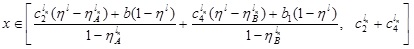 for (4.5).
for (4.5).
Hence the required LNMF 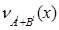 is
is

In a similar fashion, we have the UNMF 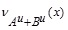 of A + B
of A + B

Thus, we have
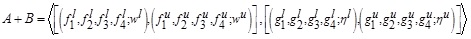
where 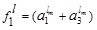

and 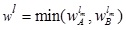 .
.

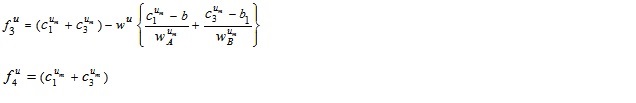
and 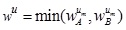
Also 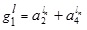
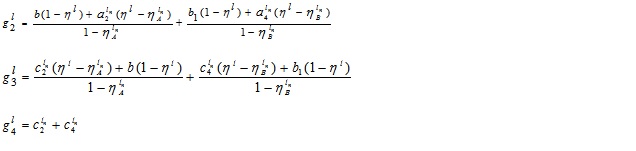
and 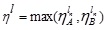
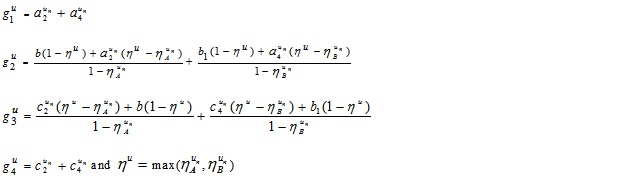
A + B is clearly a GIVTrIFN with height of the MFs are 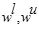 and NMFs are
and NMFs are 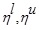 .
.
Hence the theorem.
4.2. Theorem (Subtraction of Two GIVTIFNs with Different Heights Produces a GIVTrIFNs)
4.2.1. Proof
To perform subtraction operation of GIVTIFNs A and B, we subtract the α, β-cuts of A and B using interval arithmetic.
For MF,
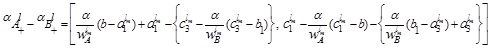 |
(4.6) |
where 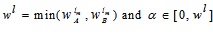 .
.
To find the membership function 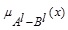 we equate both the first and second component of (4.6) to x which gives
we equate both the first and second component of (4.6) to x which gives
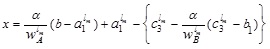 and
and 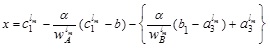
Now, expressing in terms of x
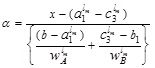 |
(4.7) |
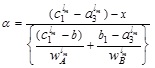 |
(4.8) |
Setting α ≥ 0 & α ≤ wL in (4.7) and α ≤ wL & α ≥ 0 in (4.8) we get the domain of x
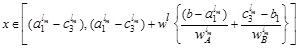 and
and 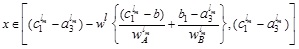
The required LMF is 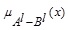
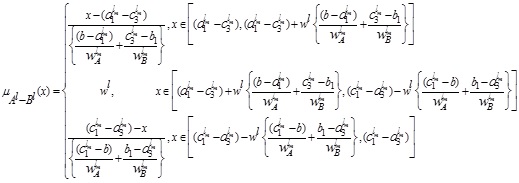
where 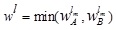 and
and 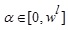 .
.
In a similar way,we can have the UMF 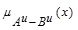 as
as
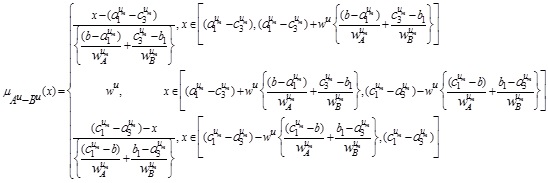
For NMFs
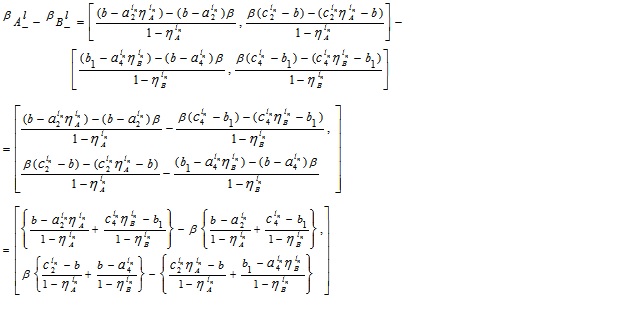
Let‘s equate each component with x, we have
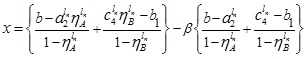
and
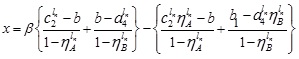
Now, expressing β in terms of x, we obtain
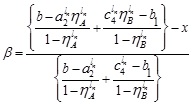 |
(4.9) |
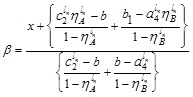 |
(4.10) |
Putting 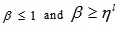 in (4.9), we have
in (4.9), we have
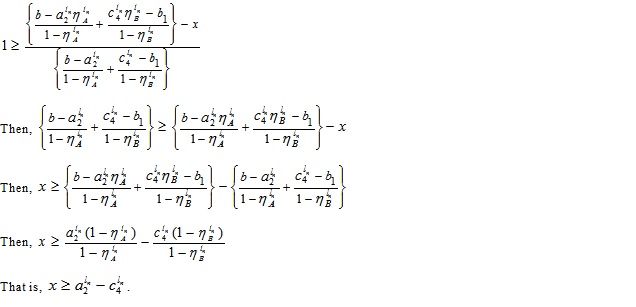
Again, taking 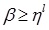 in (4.9), where,
in (4.9), where, 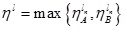 we have
we have
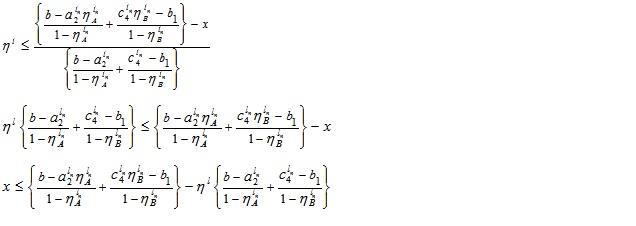
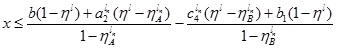
That is, 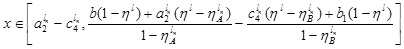 for (4.9).
for (4.9).
Next, Putting 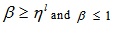 in (4.10), we have
in (4.10), we have
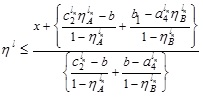 which gives
which gives
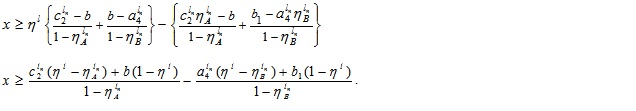
Again for β ≤ 1, we have,
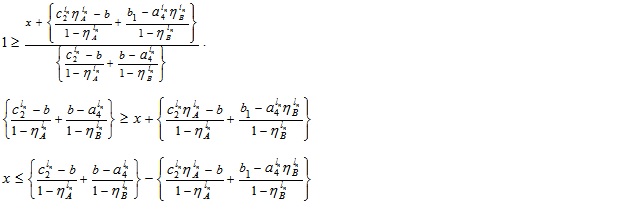
That is, 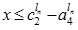 .
.
Then, 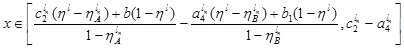 for (4.10).
for (4.10).
Hence, the required LNMF vA - B(x) is
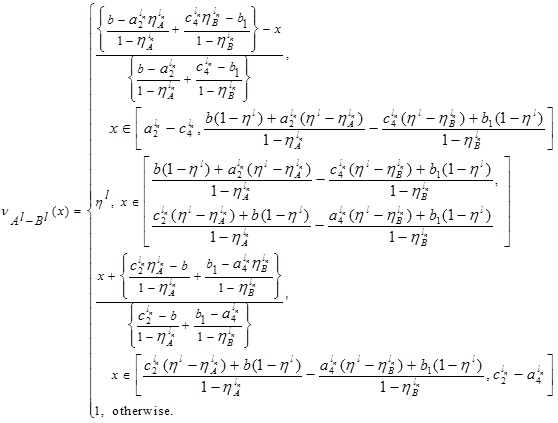
Similarly, we can have UNMF 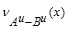 as follows:
as follows:
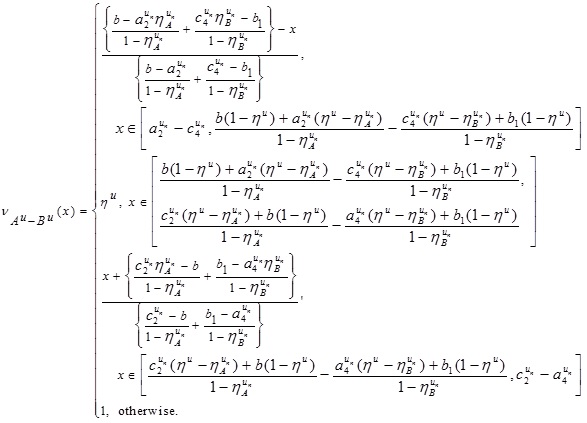
Thus, we have
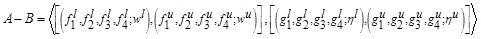
where 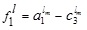
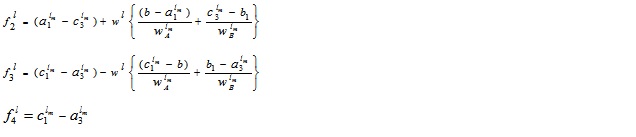
and 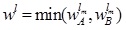 .
.
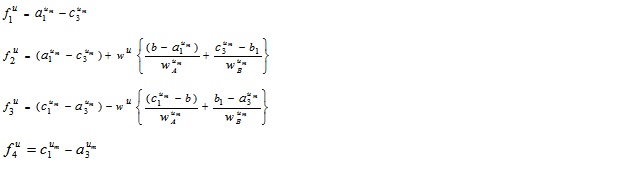
and 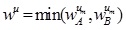
Also 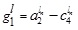
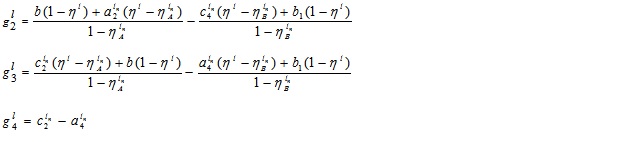
and 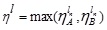
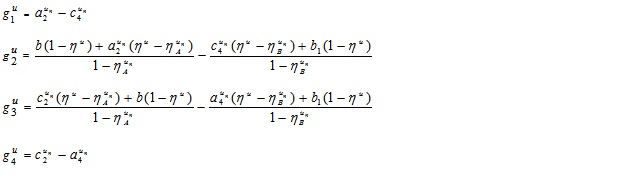
and 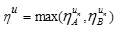
Thus, A - B is also a GIVTrIFN, where height of the MFs are  and NMFs are
and NMFs are 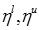 .
.
Hence proved the theorem.
4.3. Theorem (Multiplication of Two GIVTIFNs with Different Heights Produces a GIVTrIFN)
4.3.1. Proof
To calculate multiplication of GIVTIFNs A and B, we first multiply the α, β-cuts of generalized fuzzy numbers A and B using interval arithmetic.
For MF,
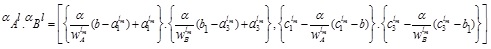 |
(4.11) |
where 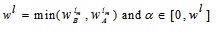 .
.
To find the LMF 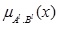 , we equate both the first and second component of (4.11) to x which gives
, we equate both the first and second component of (4.11) to x which gives
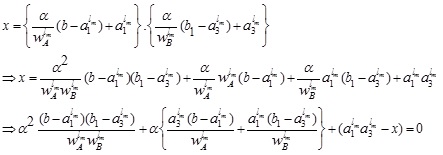
which is a quadratic equation and by solving it we obtain
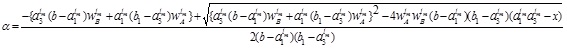 |
(4.12) |
Similarly 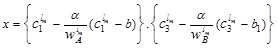 gives
gives
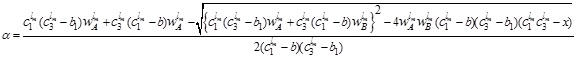 |
(4.13) |
Now, setting α ≥ 0 & α ≤ wL and α ≤ wL & α ≥ 0 in (4.12) and (4.13), we get the LMF of the resulting GIVTrIFN after multiplication of A and B together with the domain of x

Also with a similar manner, we have the UMF 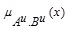 as
as

For NMF
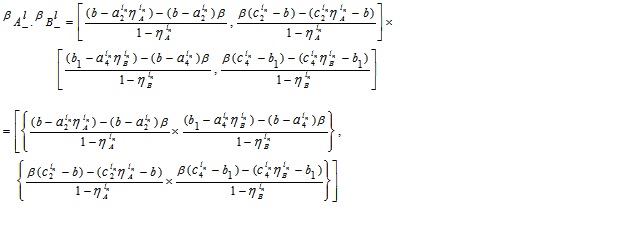
Now, equating both the terms with x, we obtain
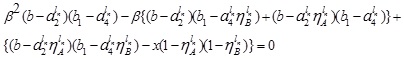
and
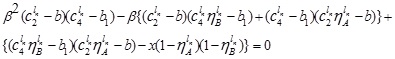
It can be expressed in terms of x by solving this quadratic equation,
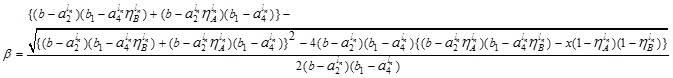 |
(4.14) |
and,
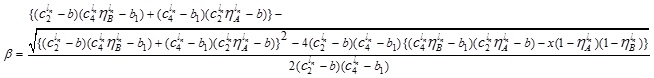 |
(4.15) |
Putting 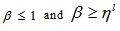 in (4.14), where
in (4.14), where 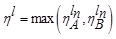 we have
we have
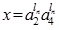 and
and
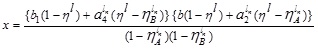
Again, 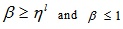 Putting and in (4.15), we have
Putting and in (4.15), we have
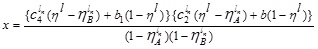
and 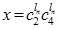 .
.
Thus, the LNMF vAB(x) is
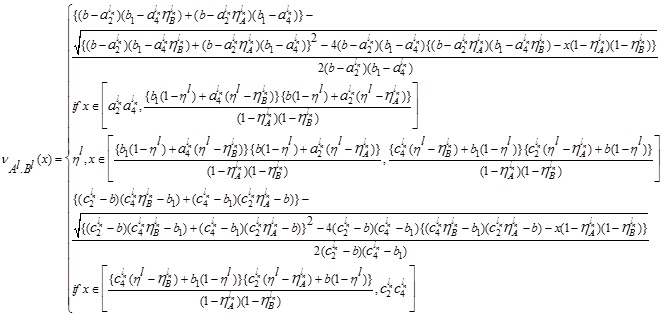
In a similar fashion, we can have UNMF 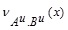 as follows:
as follows:
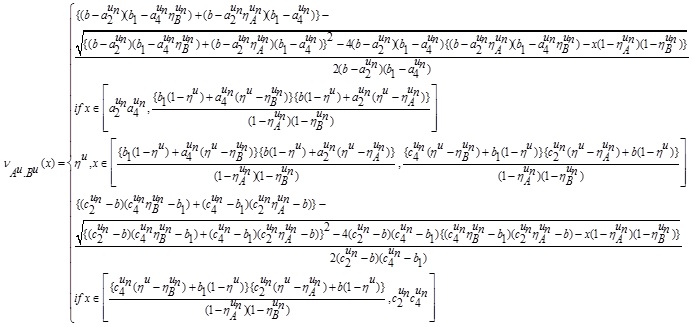
Thus, we have
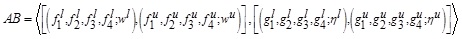
where 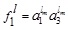
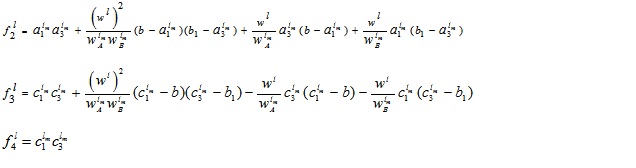
and 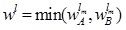 .
.
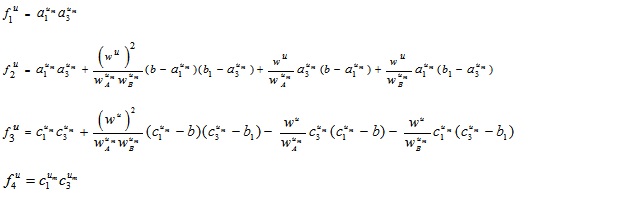
and 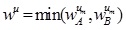
Also 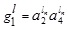
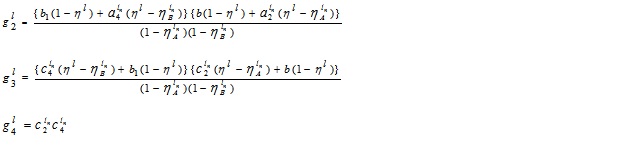
and 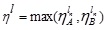
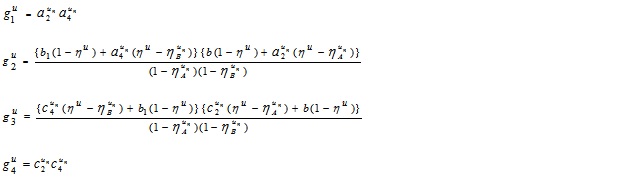
and 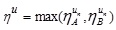
Thus, AB is clearly a type of GIVTrIFN, where height of the MFs are  and NMFs are
and NMFs are  .
.
Hence proved the theorem.
4.4. Theorem (Division of Two GIVTIFNs with Different Heights Produces a GIVTrIFNs)
4.4.1. Proof
To divide two GIVTIFNs A and B, we first divide the α, β-cuts of A and B using interval arithmetic.
For MF,
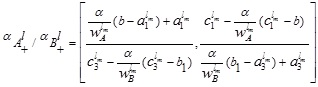 |
(4.16) |
where 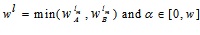 .
.
To find the LMF 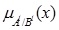 we equate both the first and second component of (4.16) to x, which gives
we equate both the first and second component of (4.16) to x, which gives
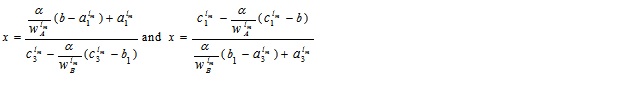
Now, expressing α in terms of x and setting α ≥ 0 & α ≤ w and α ≤ w & α ≥ 0 in the above expressions, we get α together with the domain of x
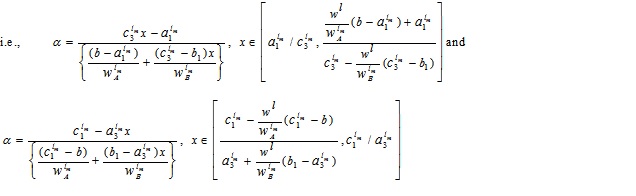
The required LMF 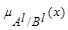 is:
is:
In a similar way, we can have the UMF  as:
as:
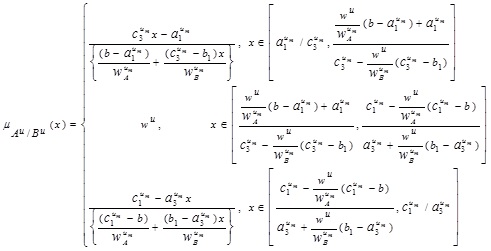
Where 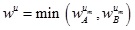 .
.
For NMF
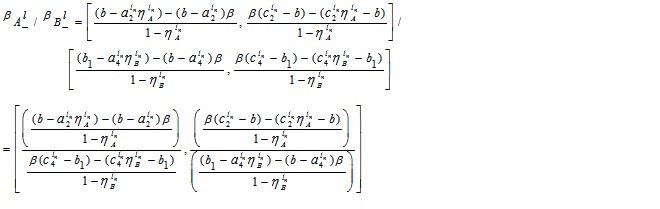
Equating each component with x, we have
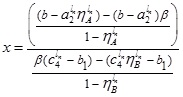
Now, expressing β in terms of x, we obtain
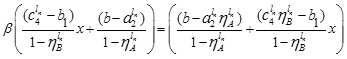
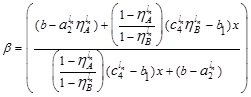 |
(4.17) |
Again, expressing 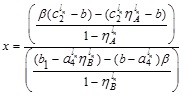 in terms of α we have
in terms of α we have
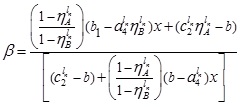 |
(4.18) |
Putting 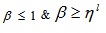 in (4.17) as well as
in (4.17) as well as 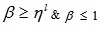 in (4.18), where
in (4.18), where 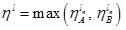 we have
we have
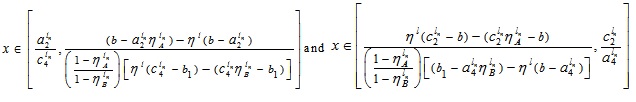
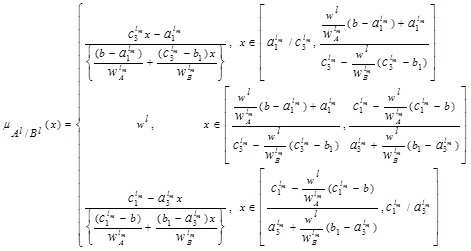
Thus, the LNMF 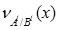 is
is
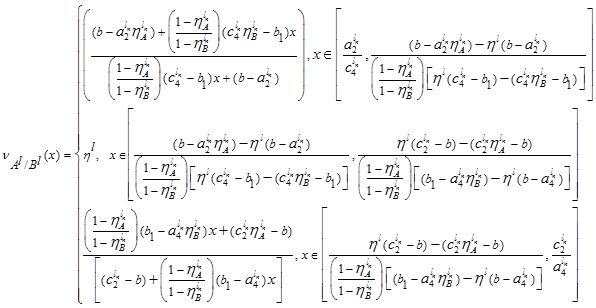
Following the same procedure, we can have the UNMF 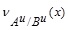 as:
as:
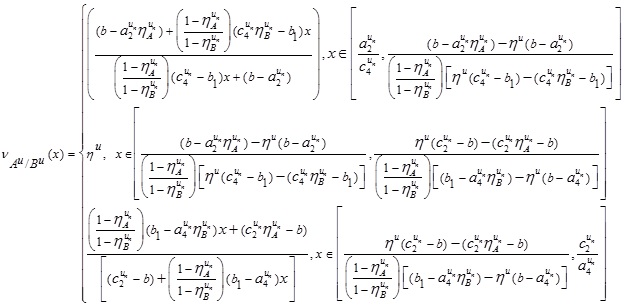
Thus,
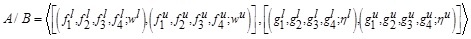
where 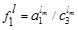

and 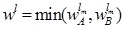 .
.

and 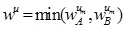 .
.
Also 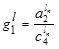
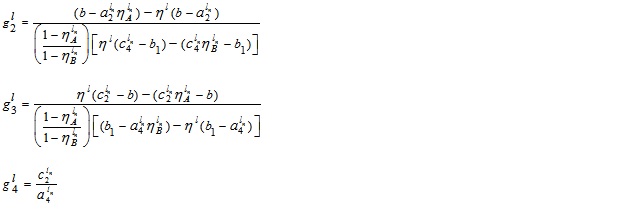
and 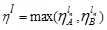
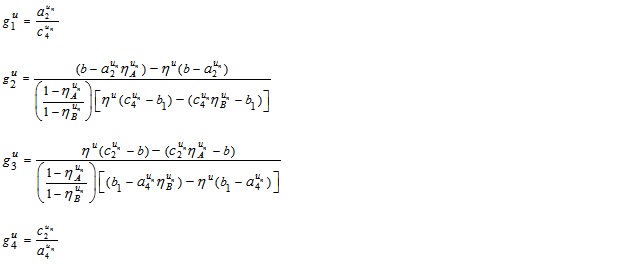
and 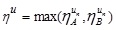
Thus, A/B is also a GIVTrIFN, where height of the MFs are 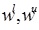 and NMFs are
and NMFs are 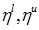 .
.
Hence proved the theorem .
4.5. Graphical Representation of the Proposed Approach
Let us consider the same example discussed in section-1 where,
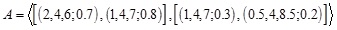 is a fixed GIVTIFN while
is a fixed GIVTIFN while
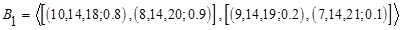 and
and 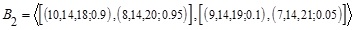 be two different GIVTIFNs with different heights. In section 1, we have seen that the existing approach [26M.H. Shu, C.H. Cheng, and J.R. Chang, "Using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly", Microelectron. Reliab., vol. 46, no. 12, pp. 2139-2148.
be two different GIVTIFNs with different heights. In section 1, we have seen that the existing approach [26M.H. Shu, C.H. Cheng, and J.R. Chang, "Using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly", Microelectron. Reliab., vol. 46, no. 12, pp. 2139-2148.
[http://dx.doi.org/10.1016/j.microrel.2006.01.007] ] produces identical GIVTIFN while carrying out the addition operation between A and B1 & A and B2 which are depicted in Figs. (8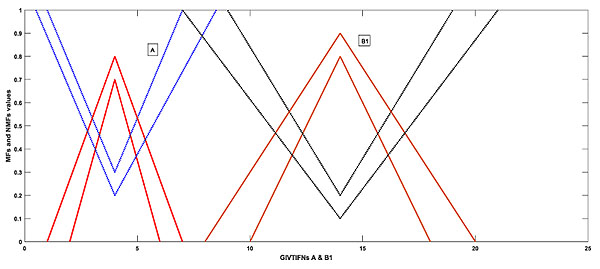 and 9
and 9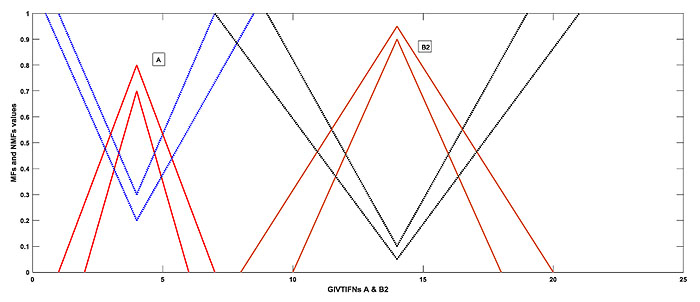 ) respectively. On the other hand, while performing the addition operation for the same pairs of GIVTIFNs by using the proposed approach, it produces two distinct GIVTrIFNs. Thus, the GIVTrIFNs are given as:
) respectively. On the other hand, while performing the addition operation for the same pairs of GIVTIFNs by using the proposed approach, it produces two distinct GIVTrIFNs. Thus, the GIVTrIFNs are given as:
 |
Fig. (8) MFs and NMFs of GIVTIFNs A and B1 |
 |
Fig. (9) MFs and NMFs of GIVTIFNs A and B2 |
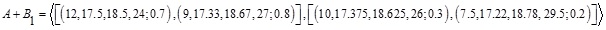 and
and 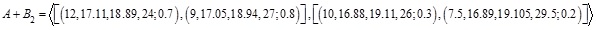 .
.
The following Figs. (10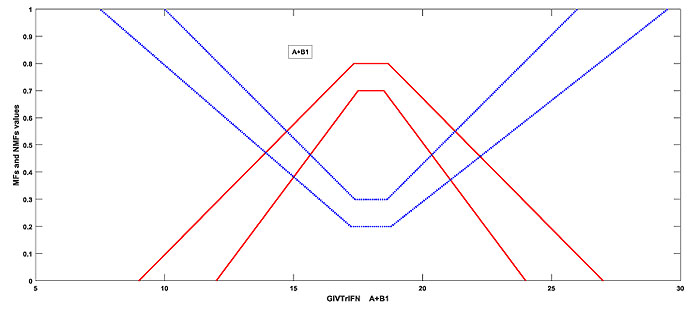 and 11
and 11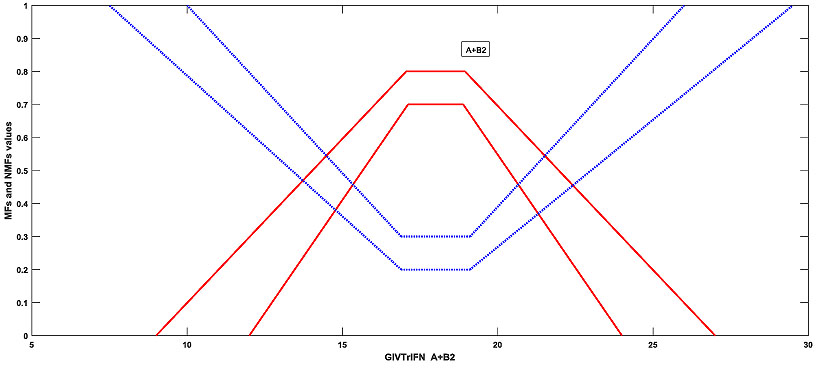 ) are the graphical representation of the GIVTrIFNs A + B1 and A + B2.
) are the graphical representation of the GIVTrIFNs A + B1 and A + B2.
 |
Fig. (10) : MFs and NMFs of GIVTrIFNs A+B1 |
 |
Fig. (11) MFs and NMFs of GIVTrIFNs A+B2 |
Similarly, different outputs will be obtained other arithmetic operations which is logical and correct while the existing approach leads to illogical output.
5. NUMERICAL EXAMPLES
Let 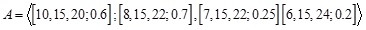 and
and 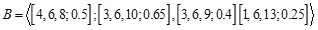 be two triangular GIFNs.
be two triangular GIFNs.
Then, using the proposed approach we have
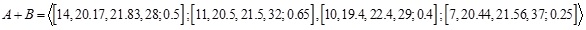
whose MFs and NMFs are:
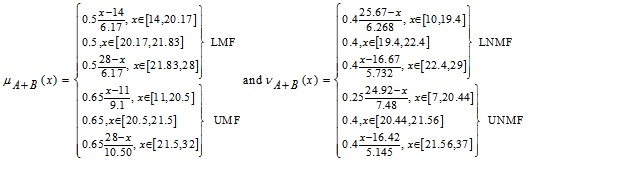
respectively.
Then, 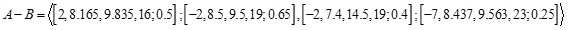 whose MFs and NMFs are:
whose MFs and NMFs are:
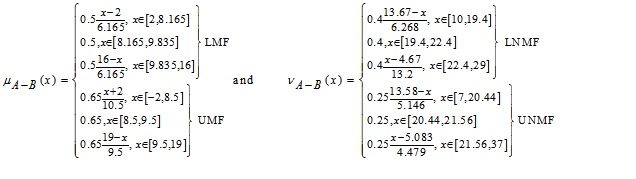
respectively.
Also 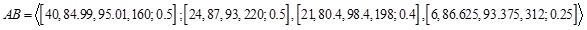 whose MFs and NMFs are:
whose MFs and NMFs are:
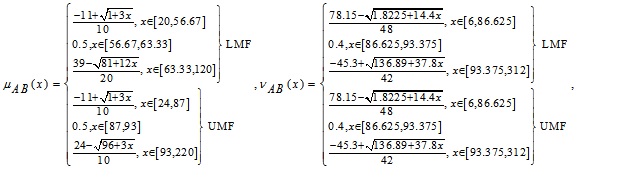
And
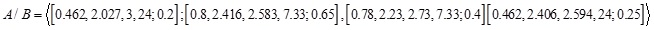
whose MFs and NMFs are
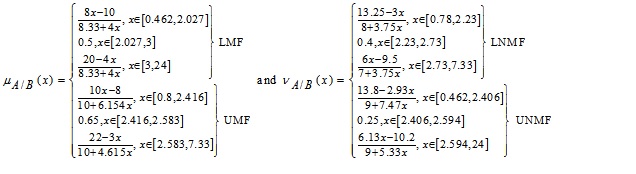
6. RANKING OF GIVTRIFNS BASED ON VALUE INDEX
Deng Feng Li [35D.F. Li, "A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems", Comput. Math. Appl., vol. 60, pp. 1557-1570.
[http://dx.doi.org/10.1016/j.camwa.2010.06.039] ] introduced the concept of value and ambiguity of GTIFN and the same concept has been put forward for GTrIFN by De and Das [36P.K. De, and D. Das, "A Study on Ranking of Trapezoidal Intuitionistic Fuzzy Numbers", Int. J. Comput. Inf. Syst. Ind. Manage. Appl., vol. 6, pp. 437-444.]. In this section, we will extend the concept of the value of GTrIFN to GIVTrIFNs.
Definition: Let 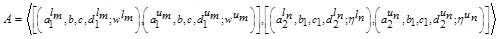 be a GIVTrIFN and
be a GIVTrIFN and 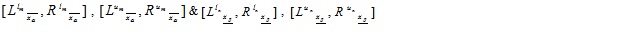 be α, β-cuts of the MFs and NMFs of A, respectively. Then the value of MFs and NMFs of A is defined as:
be α, β-cuts of the MFs and NMFs of A, respectively. Then the value of MFs and NMFs of A is defined as:
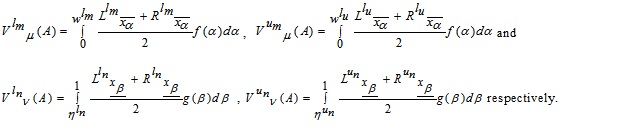
Where f(α) is a non-negative and non-decreasing function on 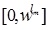 with
with 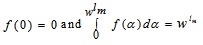 and on
and on 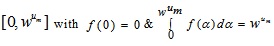 . The function f(β) is a non-negative and non-increasing function on
. The function f(β) is a non-negative and non-increasing function on 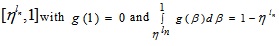 also f(β) is a non-negative and non-increasing function on
also f(β) is a non-negative and non-increasing function on 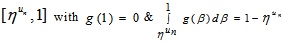
Like [35D.F. Li, "A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems", Comput. Math. Appl., vol. 60, pp. 1557-1570.
[http://dx.doi.org/10.1016/j.camwa.2010.06.039] ] and [36P.K. De, and D. Das, "A Study on Ranking of Trapezoidal Intuitionistic Fuzzy Numbers", Int. J. Comput. Inf. Syst. Ind. Manage. Appl., vol. 6, pp. 437-444.], we also choose,
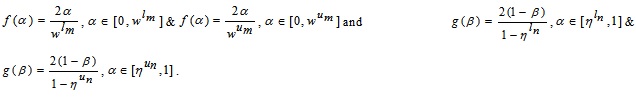
Thus the value of the MFs and NMFs of A are evaluated as:
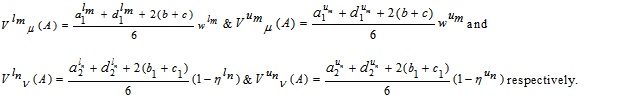
Zeng et al. [37X. Zeng, D.F. Li, and G. Yu, "A Value and Ambiguity based Ranking method of trapezoidal intuitionistic fuzzy numbers and application to Decision making", Sci. World J., pp. 1-8.], devised value-index to rank trapezoidal IFS and we extend it for GIVTrIFNs.
That is, for a GIVTrIFS
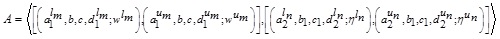 the value-index of A is defined as:
the value-index of A is defined as:
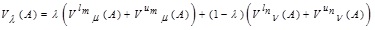 , where
, where 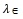 [0,1] is a weight which represents the decision maker’s preference information.
[0,1] is a weight which represents the decision maker’s preference information.
7. MULTI-CRITERIA GROUP DECISION-MAKING USING ARITHMETIC OPERATIONS ON GIVTIFNs
In general, multi-criteria group decision-making problems include uncertain imprecise data and information. For validity and justification of the approach and to show the application in real-world problem of the proposed approach, a multi-criteria group decision-making model has been carried out to rank the best alternative among the available alternatives based on GIVTIFNs.
7.1. Methodology
Let us suppose that a committee of K expert decision makers D1, D2...DK will choose the best alternative among n alternatives A1, A2,..., An based on m criteria where C1,C2,...,Cm are for each alternative respectively.
The procedure for the decision process is given below:
- Step-I: Decision makers choose linguistic weighting variables with respect to the importance weight of criteria and the linguistic ratings variable to evaluate the ratings of alternatives with respect to each criterion which are expressed in terms of positive GIVTIFNs.
- Step-II: Decision makers evaluate the importance weight of each criterion using linguistic weighting variables.
- Step-III: The weights of criteria are aggregated using.
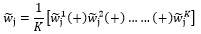 |
to get the aggregated fuzzy weight 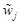 of the criterion Cj.
of the criterion Cj.
The new weight vector can be written as:
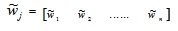 |
where each 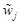 is GIVTIFNs.
is GIVTIFNs.
-
Step-IV: Decision makers give their opinion to get the aggregated fuzzy ratings
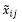 of alternative
of alternative 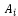 under criterion Cj. That is,
under criterion Cj. That is,
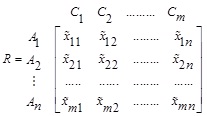 |
where each 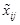 is GIVTIFNs.
is GIVTIFNs.
- Step-V: If all the weights and ratings are in the interval [0, 1] (i.e., W and R are normalized) the next step is followed and
if not, they can be normalized by:
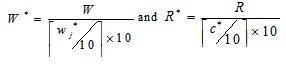 |
Where  is the ceiling function,
is the ceiling function, 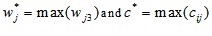 .
.
- Step-VI: Construct the weighted normalized fuzzy decision matrix
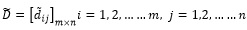
Where 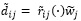 using our proposed arithmetic operations which are normalized positive GIVTIFNs.
using our proposed arithmetic operations which are normalized positive GIVTIFNs.
-
Step-VII: Decision makers evaluate
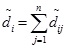 using our proposed arithmetic operations.
using our proposed arithmetic operations.
-
Step-VIII: Based on maximum value-index of
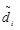 , decision-makers will choose the suitable alternative Ai.
, decision-makers will choose the suitable alternative Ai.
7.2. Hypothetical Case Study
Let us suppose a committee of three expert decision makers, D1, D2 and D3 which has been formed to conduct the interview for the post of the professor to select the most suitable candidate among the three eligible candidates, namely A1, A2 and A3. Five benefit criteria are considered:
C1: Research Publications,
C2: Teaching skills,
C3: Subject Knowledge,
C4: Experiences in teaching,
C5: Teaching discipline.
7.2.1. Computational Procedure is Discussed in Detail Below:
- Step-I: Decision makers choose the linguistic weighting variable Table 1 for the importance weight of criteria and the linguistic ratings variable Table 2 to evaluate the ratings of alternatives with respect to each criterion.
- Step-II: To assess the importance of the criteria Table 3 linguistic weighting variables are used Table 1
-
Step-III: The weights of criteria are aggregated using equation (1) to get the aggregated fuzzy weight
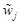 of the criterion Cj and decision makers give their opinion Table 4 to get the aggregated fuzzy ratings
of the criterion Cj and decision makers give their opinion Table 4 to get the aggregated fuzzy ratings 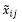 of alternative Ai under criterion Cj.
of alternative Ai under criterion Cj.
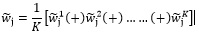

Similarly, we have

- Step-IV: The fuzzy decision matrix R is constructed as follows using Table 4.

Since all the weights and ratings are in the interval [0, 1], so the matrix R is the normalized fuzzy decision matrix.
- The weighted normalized fuzzy decision matrix is now constructed by using equation (2).
-
To evaluate
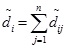 using our proposed arithmetic operations, we have
using our proposed arithmetic operations, we have

-
Step-V: It is clear from the Table 5 that the calculated value-index Vλ(A) for d2 is maximum for any given weight
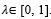 . Thus, the ordering of di's(i = 1, 2, 3) for any
. Thus, the ordering of di's(i = 1, 2, 3) for any 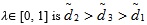 . Higher the value index of di's will indicate the best selection of the alternative Ai(i = 1, 2, 3). Hence, the ranking order of the four alternatives is A1 > A2 > A3and the best selection of the alternatives is.
. Higher the value index of di's will indicate the best selection of the alternative Ai(i = 1, 2, 3). Hence, the ranking order of the four alternatives is A1 > A2 > A3and the best selection of the alternatives is.
CONCLUSION
The basic idea of IFS is the direct generalization of FST. Later, different developments have been extended, such as IVIFNs, GIVIFNs. Evaluation of arithmetic operation between GIVIFNs is a crucial issue. Arithmetic of conventional approaches produces counterintuitive results. This paper presented a novel technique to perform arithmetic operations on GIVTIFNs which efficiently overcame the shortcomings of conventional approach. The interesting part of the proposed approach is that it produces GIVTrIFN. Numerical illustrations also corroborate the same notion. The applicability and validation of the proposed approach have been shown by solving a multi-criteria group decision-making problem. It is observed that the proposed approach is efficient, simple, logical, technically sound and general enough for implementation. Researchers may apply this approach in any field where uncertainty/ imprecision can be handled using GIVTIFNs. Also, it is seen that both the conventional approach and present approach will be identical only when height of the input GIVTIFNs is same.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEGEMENTS
Declared none.
REFERENCES
| [1] | L.A. Zadeh, "Fuzzy sets", Inf. Control, vol. 8, pp. 338-356. [http://dx.doi.org/10.1016/S0019-9958(65)90241-X] |
| [2] | S.H. Chen, "Operations on fuzzy numbers with function principal", Tamkang J. Manage. Sci., vol. 6, pp. 13-26. |
| [3] | K.T. Atanassov, "Intuitionistic fuzzy sets", Fuzzy Sets Syst., vol. 20, pp. 87-96. [http://dx.doi.org/10.1016/S0165-0114(86)80034-3] |
| [4] | K. Atanassov, and G. Gargov, "Interval valued intuitionistic fuzzy sets", Fuzzy Sets Syst., vol. 31, pp. 343-349. [http://dx.doi.org/10.1016/0165-0114(89)90205-4] |
| [5] | T.Y. Chen, "Interval valued intuitionistic fuzzy QUALIFLEX method with a likehood-based comparison approach for multiple criteria decision analysis", Inf. Sci., vol. 261, pp. 149-169. [http://dx.doi.org/10.1016/j.ins.2013.08.054] |
| [6] | T. Rashid, I. Beg, and S.M. Husnine, "Robot selection by using generalized interval-valued fuzzy numbers with TOPSIS", Appl. Soft Comput. J., vol. 21, pp. 462-468. [http://dx.doi.org/10.1016/j.asoc.2014.04.002]. [http://dx.doi.org/10.1016/j.asoc.2014.04.002] |
| [7] | B. Liu, Y. Shen, X. Chen, H. Sun, and Y. Chen, "A complex multi-attribute large-group PLS decision-making method in the interval-valued intuitionistic fuzzy environment", Appl. Math. Model., vol. 38, pp. 4512-4527. [http://dx.doi.org/10.1016/j.apm.2014.02.023]. [http://dx.doi.org/10.1016/j.apm.2014.02.023] |
| [8] | V. Lakshmana Gomathi Nayagam, S. Muralikrishnan, and G. Sivaraman, "Multi criteria decision making method based on interval valued Intuitionistic fuzzy sets", Expert Syst. Appl., vol. 38, pp. 1464-1467. [http://dx.doi.org/10.1016/j.eswa.2010.07.055] |
| [9] | E. Szmidt, and J. Kacprzyk, "Intuitionistic fuzzy sets in some medical applications", Lect. Notes Comput. Sci., vol. 2206, pp. 148-151. [http://dx.doi.org/10.1007/3-540-45493-4_19] |
| [10] | B. Davvaz, and E.H. Sadrabadi, "An application of intuitionistic fuzzy sets in medicine", Int. J. Biomath., vol. 9, pp. 16500371-15. [https://doi.org/10.1142/S1793524516500376]. [http://dx.doi.org/10.1142/S1793524516500376] |
| [11] | D.F. Li, "Fuzzy multiattribute decision making models and methods with incomplete information", Fuzzy Sets Syst., vol. 106, pp. 113-119. [http://dx.doi.org/10.1016/S0165-0114(97)00272-8] |
| [12] | K. Atanassov, G. Pasi, and R. Yager, "Intuitionistic fuzzy interpretations of multi-person multicriteria decision making", Proc. Of First Intern. IEEE Symposium Intell. Syst, vol. 1, pp. 115-119. [http://dx.doi.org/10.1109/IS.2002.1044238] |
| [13] | X. Yuan, and H. Li, "Cut sets on interval-valued intuitionistic fuzzy sets", IEEE Sixth International Conference on Fuzzy Systems and Knowledge Discovery, FSDK, vol. 6, pp. 167-171. [http://dx.doi.org/10.1109/FSKD.2009.606] |
| [14] | X. Yuan, H. Li, and S. Kaibiao, "Theory based on interval-valued level cut sets of Zadeh fuzzy sets", Fuzzy Information and Engineering, vol. 2, pp. 501-510. [http://dx.doi.org/10.1007/978-3-642-03664-4_55] |
| [15] | R.R. Yager, "Some aspects of intuitionistic fuzzy sets", Fuzzy Optim. Decis. Making, vol. 8, pp. 67-90. [http://dx.doi.org/10.1007/s10700-009-9052-7] |
| [16] | E. Szmidt, and J. Kacprzyk, "Dilemmas with distances between intuitionstic fuzzy sets: Straightforward approaches may not work", Studies in Computational Intelligence, vol. 109, pp. 415-430. |
| [17] | X. Zeishui, "On similarity measures of interval-valued intuitionistic fuzzy sets and their application to pattern recognitions", J. Southeast Univ., vol. 23, pp. 139-143. [English Edition]. |
| [18] | Z. Qiansheng, Y. Haixiang, and Z. Zhenhua, "Some similarity measures of interval-Valued intuitionistic fuzzy sets and application to pattern recognition", Appl. Mech. Mater., vol. 44-47, pp. 3888-3892. [https://doi.org/10.4028/www.scientific.net/AMM.44-47.3888]. |
| [19] | Z. Qiansheng, J. Shengyi, J. Baoguo, and L. Shihua, "Some information measures for interval-valued intuitionistic fuzzy sets", Inf. Sci., vol. 180, no. 12, pp. 5130-5145. |
| [20] | Z. Qiansheng, Y. Haixiang, and Z. Zhenhua, "An interval-valued fuzzy reasoning approach based on weighted similarity measure", Adv. Mat. Res., pp. 143-144. |
| [21] | S. Xiaoyong, L. Yingjie, H. Jixue, and S. Zhaohui, "Description and reasoning method of uncertain temporal knowledge based on IFTPN", Control Decis., vol. 25, no. 10, pp. 1457-1462. |
| [22] | X. Zeshui, and R.R. Yager, "Intuitionistic and interval-valued intuitionistic fuzzy preference relations and their measures of similarity for the evaluation of agreement within a group", Fuzzy Optim. Decis. Making, vol. 8, pp. 123-139. [http://dx.doi.org/10.1007/s10700-009-9056-3] |
| [23] | L. Dengfeng, "Topsis-Based Nonlinear-Programming methodology for multiattribute decision making with Interval-valued intuitionistic fuzzy sets", IEEE Trans. Fuzzy Syst., vol. 18, no. 2, pp. 299-311. |
| [24] | L. Dengfeng, "Mathematical-Programming approach to matrix games with payoffs represented by Atanassov’s Interval- valued intuitionistic fuzzy sets", IEEE Trans. Fuzzy Syst., vol. 18, no. 6, pp. 1112-1128. [http://dx.doi.org/10.1109/TFUZZ.2010.2065812] |
| [25] | T.K. Mondal, and S.K. Samanta, "Generalized intuitionistic fuzzy sets", Journal of Fuzzy Mathematics, vol. 10, pp. 839-861. |
| [26] | M.H. Shu, C.H. Cheng, and J.R. Chang, "Using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly", Microelectron. Reliab., vol. 46, no. 12, pp. 2139-2148. [http://dx.doi.org/10.1016/j.microrel.2006.01.007] |
| [27] | L. Dengfeng, "A note on using intuitionistic fuzzy sets for fault-tree analysis on printed circuit board assembly", Microelectron. Reliab., vol. 48, p. 1741. [http://dx.doi.org/10.1016/j.microrel.2008.07.059] |
| [28] | Z. Zhenhua, Y. Jingyu, Y. Youpei, and Z. Qiansheng, "A Generalized Interval Valued Intuitionistic Fuzzy Sets theory", Advanced in Control Engineering and Information Science, vol. 15, pp. 2037-2041. |
| [29] | M. Bhowmik, "Some results on Generalized Interval valued Intuitionistic Fuzzy sets", Int. J. Fuzzy Syst., vol. 14, no. 2, . |
| [30] | P.E.I. Zhi, L.U. Jian-Sha, and Z.H.E.N.G. Li, "Generalized Interval valuedIntuitionistic Fuzzy Numbers with Application in Workstation Assessment", System Engineering Theory & practice, vol. 32, no. 10, pp. 2198-2206. |
| [31] | A.K. Adak, M. Bhowmik, and M. Pal, Decomposition Theorem of Generalized Interval valued Intuitionistic Fuzzy Sets., Contemporary Advancement in Information Technology Development in Dynamic Environment, . [DOI: 10.4018/978-1-4666-6252-0.ch009] [http://dx.doi.org/10.4018/978-1-4666-6252-0.ch009] |
| [32] | E. Baloui Jamkhaneh, and S. Nadarajah, "A New generalized intuitionistic fuzzy sets", Hacet. J. Math. Stat., vol. 44, no. 6, pp. 1537-1551. |
| [33] | A. Shabani, and E. Baloui Jamkhaneh, "A new generalized intuitionistic fuzzy numbers", J. Fuzzy Set Valued Anal., vol. 4, pp. 1-10. [http://dx.doi.org/10.5899/2014/jfsva-00199] |
| [34] | E. Baloui Jamkhaneh, "New generalized interval valued intuitionistic fuzzy sets", Res. Commun. Math. Math. Sci., vol. 5, no. 1, pp. 33-46. |
| [35] | D.F. Li, "A ratio ranking method of triangular intuitionistic fuzzy numbers and its application to MADM problems", Comput. Math. Appl., vol. 60, pp. 1557-1570. [http://dx.doi.org/10.1016/j.camwa.2010.06.039] |
| [36] | P.K. De, and D. Das, "A Study on Ranking of Trapezoidal Intuitionistic Fuzzy Numbers", Int. J. Comput. Inf. Syst. Ind. Manage. Appl., vol. 6, pp. 437-444. |
| [37] | X. Zeng, D.F. Li, and G. Yu, "A Value and Ambiguity based Ranking method of trapezoidal intuitionistic fuzzy numbers and application to Decision making", Sci. World J., pp. 1-8. |