Permanent magnet wind generator (PMWG) has the advantages of stable running, high efficiency and good reliability, which made them widely used in wind power systems [1F. Wang, "Application and development tendency of PM machines in wind power generation system", Transactions of China Electrotechnical Society, vol. 3, pp. 12-24, 2012. (in chinese), 2H. Tian, R. Tang, and L. Yan, "Thermal analysis and calculation of PMWGs", Transactions of China Electrotechnical Society, vol. 28, no. 3, pp. 122-126, 2013. (in chinese)]. The AC output power must be converted into DC through the rectifier firstly, and then, part of the DC accessed to DC equipment storage, the other part was converted into AC for accessing the power grid. As a result, power rectifier is the critical component of the wind power system.

In the process of wind generator access to the power grid, the rectifier could use IGBT PWM rectifier or diode rectifier. This paper was focused on these nonlinear characteristics and the influence of rectifiers on generator was studied. The function of no-control rectifier has the advantages of simple manufacturing, low cost and good rectifying effect. So, this paper uses diode rectifier in the rectification process.

Many experts and scholars put forward various control strategies to achieve high quality access to electric power grid and superior performance of low voltage across. Those researches are listed in the references [3C. Xia, "Wind energy conversion system based on PMSG and its power converter technology", Transactions of China Electrotechnical Society, vol. 11, pp. 1-13, 2012. (in chinese)-9Y. Ma, X. Li, and Z. Xu, "A Unified Model of Grid-Connected Distributed Generation through Inverters", Transactions of China Electrotechnical Society, vol. 28, pp. 145-154, 2013.].

They mainly focused on the inverter control algorithm and the quality of the grid output power, that is, the influences of converter on PMWG were ignored. So, this article studied the influences of rectifier on generator`s electromagnetic field and temperature field by using the field-circuit coupling method.

Taking the PMWG and rectifier as the research targets, the system model and external circuit were established. Firstly, based on the field-circuit coupling calculation method, the line voltage and current harmonics were studied when the generator was connected to rectifier loads and pure resistance loads respectively, so did the total harmonic distortion. The mechanism of harmonic impacted by rectifiers was revealed. Secondly, the harmonic electromagnetic field theory was studied, the stator core loss, armature winding copper loss and rotor eddy loss were analyzed when the generator connected to different loads respectively. Furthermore, according to the definition of nonlinear circuits PF, the numerical analysis method was adopted to calculate the power factor when the generator connected two loads respectively. The change mechanism of PF impacted by rectifiers has been revealed. In addition, the temperature field model has been established and the generator temperature was also analyzed. The temperature distributions were obtained when the wind generator was connected to different loads. Then, the relationship between losses and temperature was considered, the change rules of permanent magnet temperature by the eddy current loss were studied under different load. At last, it can prove that the rectifiers have influences on both electromagnetic field and temperature field through comparing the simulation results with the experimental test data.

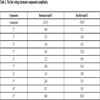
In order to study the influences of rectifier on PMWG various electromagnetic field parameters, the electromagnetic field model of PMWG was established based on the finite element theory, as shown in Fig. (1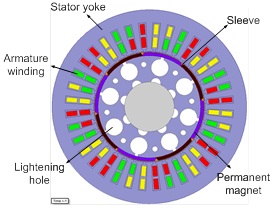). The basic parameters of the PMWG are listed in Table 1.

Fig. (1) The model of PMWG.

Table 1.
Basic parameters of PMWG.

Based on field-circuit coupling theory and the principle of load power is constant, the PMWG external circuit was designed in this research. The prime mover speed is 104.7rad/s, the rated power P ₀ is 8kW and the no-load rated output phase voltage U ₀ is 225V.

(1) In order to study the PMWG various electromagnetic field parameters when it was connected to resistance load, the whole model of purely resistance loads connected to the generator is established, as shown in Fig. (2).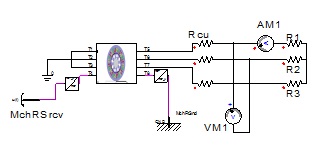

Fig. (2) The model of PMWG connected to the resistance.

In Fig. (2), the parameters determine process of Y type three-phase resistors (R₁, R₂, R₃) were as follows:

Because the external circuit is the Y type three-phase circuit, each resistance distributes the total power averagely. Formula (1) was as follows:

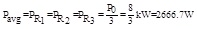(1)

Where P_avg represents each Y type three-phase load average distribution of power.

According to the power calculation, formula (2) was as follows:

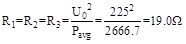(2)

But, the output phase voltage dropped when the generator connected to load. The voltage is lower than the no-load rated output phase voltage. So the resistance 19.0Ω in the formula (2) is the maximum resistance theoretically.

In order to keep the output power maintaining 8kW, the resistances should gradually reduce by using the heuristics and iteration method. In all, when the generator was connected to the resistance, the theory resistance is 19.0Ω and the actual resistance is 11.2Ω in engineering permissible error range (±5%).

(2) In order to compare PMWG connected the pure resistance load with PMWG connected the rectifier load, so as to find the influences of rectifier on PMWG electromagnetic field, the model of PMWG connected to the rectifier load was established, as shown in Fig. (3).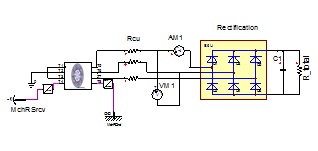

Fig. (3) The model of PMWG connected to the rectifier.

3.1. The Load Parameters Determination in Fig. (3)

When the generator connected to the rectifier, the load current became DC. The load could be described as one-single R_total.

Based on the reference [10Z. Wang, and H. Jun, Power Electronics., China Machine Press: Beijing, 2001, pp. 61-66.], the relationship between the input AC voltage and the output DC voltage in uncontrolled three-phase bridge rectifier with capacitor filter circuit was as follows:

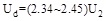(3)

Where U_d is the rectifier output DC voltage, U₂ is the output phase voltage in generator.

When the generator was connected to nothing, the phase voltage was equal to no-load voltage whose value is 225V. Due to the influence of armature reaction, as long as the load was connected, the output voltage reduced. So, when the generator output power keeps 8kW, U₂=196.3V.

According to the value of U₂, U_d could be confirmed.

Because the generator no-load coefficient maximum value equals to 2.45, and the fact of coefficient is reduced when the load is increased.

This paper based on the no-load generator output voltage coefficient to determine the upper limit resistance. The determination process was as follows.

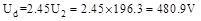(4)

The filter capacitor voltage on both sides is:

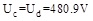(5)

Under the condition of guarantee the load power constant equals 8kW, R was concluded like:

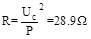(6)

Similarly, compared with no-load situation, the armature reaction leads to the output voltage decreased when the generator was connected to any type of loads. The output voltage decreased caused the situation that actual output power is not the on-load output voltage when the generator was connected to loads.

According to the nonlinear relationship between the increased external resistance and the changed load voltage, the total resistance load was calculated by using the iterative method. Gradually reduced the no-load situation calculated resistance at the rated power, the actual rectifier load is 17.2Ω.

3.2. The Filter Capacitor Parameters Determination

According to the calculated method in the reference [11S. Chwirka, Power Converter Design Using the Saber Simulator. Analogy, Inc., Beaverton, Oregon, 2002.], the determine process of filter capacitor value was shown as follows. Fig. (4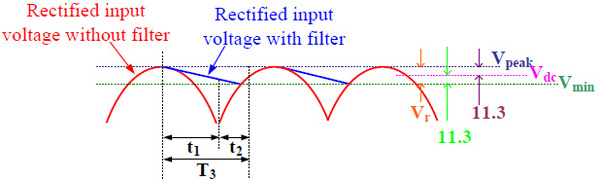) described the filtering process.

Fig. (4) The capacitor filtering process.

According to Fig. (4):

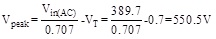(7)

Where V_peak is the maximum voltage before capacitor filter, V_in(AC) is the PMWG no-load output line voltage 389.7V, V_T is the diode voltage drop.

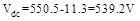(8)

Where V_dc is the DC voltage.

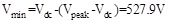(9)

Where V_min is minimum voltage value after capacitance filtering.

Filter capacitor value calculation formula is:

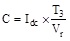(10)

Where I_dc is the equivalent current after rectifying filtering, T₃ is the filter capacitor function time in a cycle time, V_r is the difference between the value before the capacitor filtering and the value after the filtering.

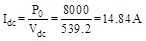(11)

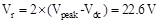(12)

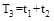(13)

The calculation method of t₁, t₂ was as follows:

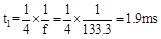(14)

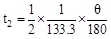(15)

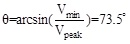(16)

So, t₂ = 1.5ms, and it could obtain that:

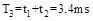(17)

According to the formula (10), C = 2.23 mF. But, the capacitor value 2.23mF is a theory value which could barely meet the capacitor filtering model needs when the generator was working on the stable situation. In order to have better filtering effect and safety margin, the filter capacitance value was determined into 10 mF. In all, when the PMWG was connected to the rectifier load, the external circuit resistance is 17.2Ω, and the filter capacitance is 10mF.

This chapter analyzed the generator output line voltage, output current, losses and power factor when the PMWG was connected to the pure resistance load and rectifier load respectively. Therefore, the influence of rectifier on electromagnetic field was obtained.

4.1. The Influence of Rectifier on Voltage Harmonic and Current Harmonic

Fig. (5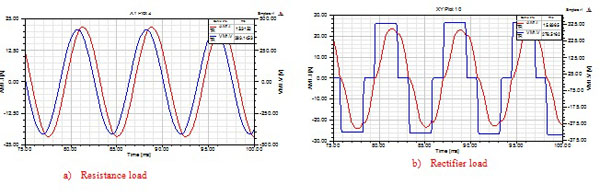) showed the line voltage and current waveform of PMWG when it was connected to the 8kW resistance and rectifier load respectively at the speed of 2000r/min.

As shown in Fig. (5), the PMWG output line voltage and current were closed to the sine wave when it was connected to resistance load.

According to Fig. (5b), it is obviously to see the output current was closed to sine wave when the generator connected to the rectifier load, but the sine degree of the output line voltage was very low because the fast on-off transitions of rectifier.

Fig. (5) The waveform of generator output voltage and current.

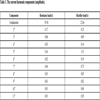
In order to precisely study the output line voltage and current harmonic content when the generator connected to two different loads, this paper decomposed the output line voltage and current based on the theory of Fourier decomposition respectively. The fundamental and harmonic components were shown in Tables 2 and 3.

Table 2
The line voltage harmonic components (amplitude).

Table 3
The current harmonic components (amplitude).

According to Tables 2 and 3 when the generator was connected to resistance load at rated speed, the biggest voltage harmonic ratio was 1.33% and the largest current harmonic ratio was 0.87%. When the generator was connected to rectifier load at rated speed, the biggest voltage harmonic ratio was 19.1% and the largest current harmonic ratio was 6.85%.

So, when the PMWG was connected to the rectifier, the line voltage and current harmonic components all increased.

Because the ratio of fundamental wave and harmonic wave could accurately reflect the influence of harmonic on waveform of output voltage and current, Fig. (6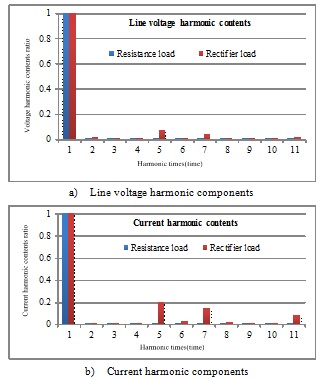) shows the ratio of each harmonic and fundamental wave when the generator was connected to different loads.

Fig. (6) Voltage and current harmonic contents.

In Fig. (6a), the abscissa is harmonic frequency, the ordinate is the harmonic content ratio, which represents the ratio of each harmonic and fundamental composition.

Fig. (6a) shows that the output line voltage 5^th, 7^th, harmonics increased obviously when the generator was connected to rectifier. Fig. (6b) shows that the output current 5^th, 7^th, 11^th harmonics increased obviously when the generator was connected to rectifier.

Voltage total harmonic distortion (THD_u) could represent the change of voltage total harmonic contents, its computation formula is:

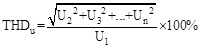(18)

Where U_n is the n^th harmonic line voltage RMS, U₁ is the fundamental line voltage RMS.

The line voltage THD was 1.5% when the generator was connected to pure resistance load. The line voltage THD could reach 25.3% when it was connected to rectifier load. So, the rectifier load caused 16.8 times as fast as the pure resistance load in output line voltage.

4.2. The Influence of Rectifier on Losses

When the PMWG was connected to the rectifier, the increased harmonic content will further affect the losses. So, the stator core loss, copper loss and the rotor eddy current loss were studied and the influence of rectifier on losses was found out.

4.2.1. The Armature Winding Copper Loss

The armature winding copper loss calculation formula is:

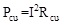(19)

Where P_cu is the copper loss, I is the output current RMS, R_cu is the armature resistance.

When the generator was connected to the resistance loads, its output current I₁=15.3A, and the each phase armature resistance equals 0.2Ω. According to ohm's law, the armature winding copper loss is 140.4W.

When the generator was connected to rectifier loads, its output current I₂=15.8A, and the armature winding copper loss is 149.8W.

The stator iron core loss and the rotor eddy current loss were calculated by finite element simulation, the data is shown in Table 4.

Table 4
The generator losses RMS.

Table 4 shows the armature winding stator core loss, copper loss and the rotor eddy current loss RMS in a steady-state cycle when the generator was connected to two loads respectively.

According to 4, when the PMWG was connected to rectifier load, the stator core loss was reduced by 10.1%, the armature winding copper loss was increased by 35.5%, and the eddy current loss was increased 9.4 times compared with the generator was connected to pure resistance load.

4.2.2. The Stator Core Loss

Stator core loss was decreased when the generator was connected to the rectifier. The reason is the change of the magnetic flux density. In the PMWG, in order to get similarity to DC motor control characteristic, a coordinate system on the rotor was established. The synchronous rotating coordinate system was with the rotor magnetic field. The rotor magnetic field direction was d axis and its perpendicular direction was q axis.

When the generator was connected to pure resistance load, the power factor equaled 1, and the angle between d axis and q axis was 90°. When generator was connected to rectifier load, the power factor was decreased (according to section 3.4 for power factor analysis). The current phase lagged behind the voltage phase, which made the angle between d axis and q axis was more than 90°. The q axis direction appeared a magnetic flux density which was on the contrary to the s axis. It reduced d axis component, thus reduced the magnetic flux density of the generator at the same time.

The classic stator core loss calculation method is the Bertotti calculation model, and the formula is:

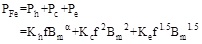(20)

Where P_Fe is the core loss, P_h is the hysteresis loss, P_c is the classical eddy current loss, P_e is the abnormal eddy current loss, K_h and α are hysteresis loss coefficient, K_c is the classical eddy current loss coefficient, K_e is the abnormal eddy current loss coefficient, f is the magnetic flux alternating frequency, B_m is the magnetic flux density [12X. Kong, F. Wang, and Y. Xu, "Analysis and calculation of iron losses of high-speed permanent magnet machines", Electric Machines and Control, vol. 14, no. 9, pp. 26-30, 2010. (in Chinese), 13Y. Li, H. Qiansheng, and C. Yang, "Analysis and calculation of the iron losses of high speed permanent motor", Small & Special Electrical Machines, vol. 36, no. 3, pp. 11-13, 2008. (in Chinese)]. Because B_m is the only reduced element in formula (20), the stator core loss was reduced.

4.2.3. The Rotor Sleeve Eddy Current Loss

In the surface magnetic rotor permanent magnet generator, the rotor sleeve is an essential part. It could protect the permanent magnet don't fall off, also could provide part of the preloading stress.

The sleeve material is divided into two kinds, alloy material and carbon fiber material. Because the alloy material is better than carbon fiber in thermal conductivity and manufacturing process, it is widely used in generator sleeve. However, the eddy current was inducted in alloy material sleeve and permanent magnet at the same time.

The fast on-off transitions of the rectifier increase the distortion of the current. The time harmonics magnetic field caused by the distorted current is not in synchronous rotate with the rotor and the sleeve. The eddy current loss is produced because the rotor and sleeve are conductive objects. So, the eddy current loss is increased by the rectifier largely.

Fig. (7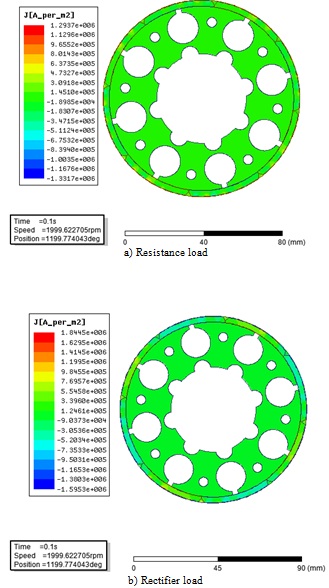) describes the eddy current density in the rotor sleeve and permanent magnet when the generator was connected to pure resistance load and the rectifier load respectively.

Fig. (7) The distribution of eddy current density of rotor, permanent magnet.

From Fig. (7), when the generator was connected to rectifier loads, the total eddy current was increased, and eddy current maximum value was appeared on the rotor sleeve. When the generator was connected to pure resistance load, the maximum eddy current density was 1.29×10⁶A/m². When the generator was connected to pure resistance load, the maximum eddy current density was 1.84×10⁶A/m², which is the 1.42 times as the generator was connected to pure resistance load.

4.3. The Change of Phase Voltage and Current RMS

This section analyzed the change of the phase voltage and current RMS. Table 5 describes the values of the phase voltage and current RMS when PMWG was connected to the pure resistance load and rectifier load respectively.

Table 5
The comparison of output voltage RMS.

From Table 5, under the condition of same output power, the output phase voltage was reduced by 15.2V and the output current was increased by 0.5A when the generator was connected to different loads respectively.

4.4. The Influence of Rectifier on Power Factor

When the generator was connected to three-phase bridge uncontrolled rectifier, it had influence on harmonic magnetic field and loss value. Furthermore, it also had effects on power factor, reduced the performance of permanent magnet excitation.

Because both voltage and current had some harmonic components, which mean they are not pure sine wave. The power factor calculation formula in the linear circuit can't apply in this nonlinear circuit. According to the initial definition of power factor, that is, the ratio of active power and apparent power, the power factor in nonlinear circuit could be obtained.

Each harmonic current usually has a sine or cosine cycle, the n^th harmonic current RMS could be obtained by the following formula:

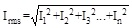(21)

Where I₁ is the fundamental current RMS, I₂, I₃,...I_n is the 2^th,3^th,…, n^th harmonic current RMS respectively.

The current total harmonic distortion rate was defined as:

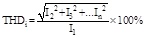(22)

According to the definition of PF in nonlinear circuit:

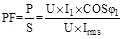(23)

Where φ₁ is the fundamental wave phase shifting angle.

Taking (21) into (22), the THD_i was described as:

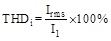(24)

Taking (27) into (26), the PF was described as:

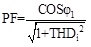(25)

When φ₁=0, PF was obtained as follows:

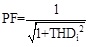(26)

The current THD is 5.5% when the generator was connected to resistance load and the current THD is 9.4% when the generator was connected to rectifier load. According to the above analysis and calculation, it was concluded that the power factor was reduced from 1 to 0.99 because the bad influence of the current total harmonic distortion when the generator was connected to the rectifier. Compared with the generator was connected to the pure resistance load, when the generator was connected to rectifier load, the excitation performance of permanent magnet was weakened, the output voltage RMS was dropped, output voltage harmonic was increased and the output power factor was decreased.

In order to verify the model contribution and the theoretical analysis, this article builds the experiment platform and gets test data. Fig. (8) shows the experiment platform. Moreover, the platform also includes Ametek MX30 variable frequency power supply, YOKOGAWA power analyzer, 10mF electrolytic capacitor, resistor and other equipment.

Fig. (8) Experiment platform of PMWG.

Fig. (9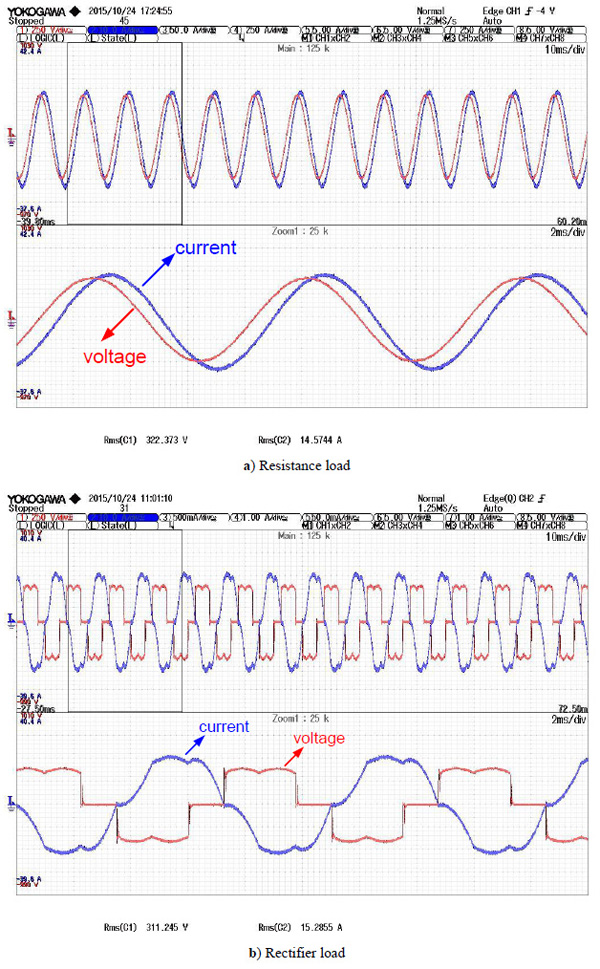) shows the waveforms of line voltage and current when PMWG was connected to different loads at the rated conditions.

Fig. (9) The test waveform of the voltage and current.

Comparing Figs. (5) and (9), it was verified the experiment waveforms and simulation waveforms. Comparing the data in Table 5 and data in Fig. (9), it was concluded that the simulation data and experimental data were basically identical. So, the experimental results verified the influence of the rectifier load on the generator electromagnetic field.

The permanent magnet in the PMWG is very sensitive to temperature and it is the high failure rate part caused by the temperature change. Especially, when the temperature reached a certain degree, it was occurred excitation-loss fault, which means, it was necessary to study the temperature field [14L. Wang, X. Yu, and Z. Yi, " Effect of temperature on magnetic performance of 33EH high quality sintered NdFeB permanent magnets", Small & Special Electrical Machines Special Steel, vol. 36, no. 1, pp. 45-48, 2015. (in Chinese).].

The PMWG temperature field model was presented in this paper. First, the whole temperature change situation in PMWG was analyzed when it was connected to two loads respectively. Then, the influence of rectifier on the permanent magnet temperature field was mainly focused on.

When the PMWG was connected to different loads respectively, the whole region two-dimensional temperature distribution is shown in 10.

According to 10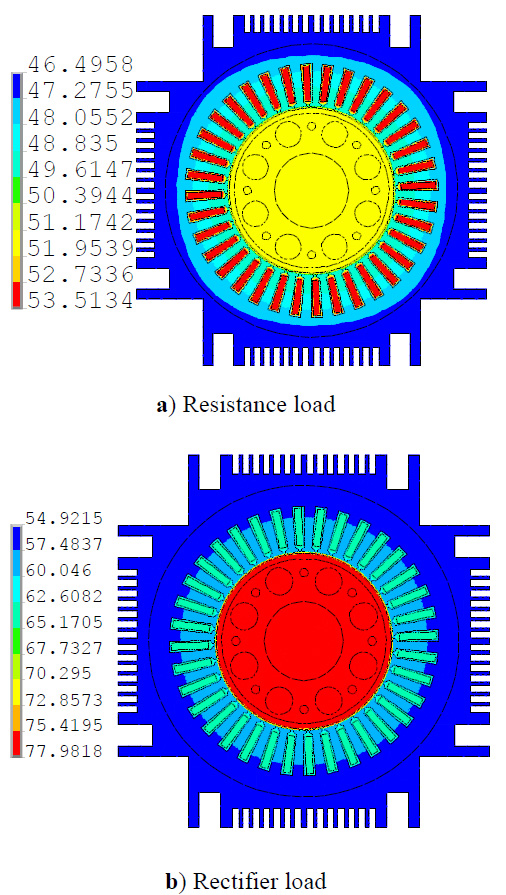, the loss is relatively small when the generator was connected to resistance load. The stator winding temperature had the similar temperature with rotor temperature. It was affected by the copper loss. However, when the generator was connected to the nonlinear loads, it was affected by the sharply increased eddy current loss. Limited by the cooling conditions, the rotor temperature was significantly higher than the stator winding temperature.

Fig. (10) The distribution of temperature distribution.

In addition, according to the whole temperature contrast in Fig. (10), when the generator was connected to the rectifier nonlinear loads, each part of the temperature distribution was significantly higher than the situation that when generator was connected to resistance load. The highest temperature in stator was increased by 18.1%. The highest rotor temperature was raised by 45.7%. Obviously, the rectifier caused the temperature significance rise.

Permanent magnetic material is the most temperature sensitive part of the PMWG. As the main factor of excitation-loss fault occurred, it had great significance to study the PMWG temperature. Fig. (11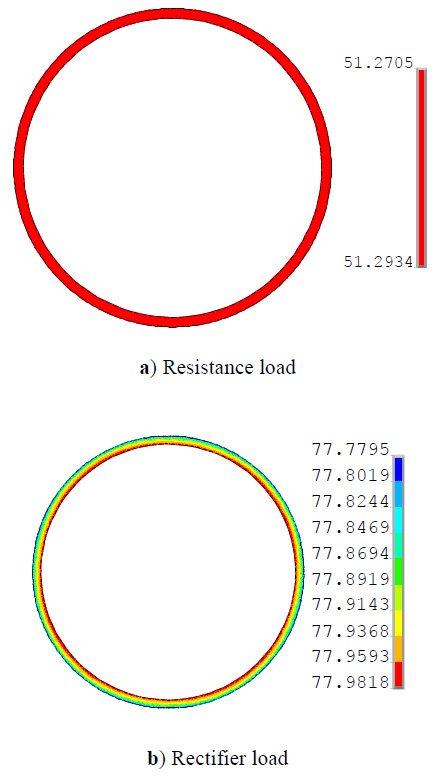) gives the permanent magnet temperature distribution when the generator was connected to different loads respectively.

Fig. (11) The temperature distribution of permanent magnet.

Combined with Fig. (10) and Fig. (11), the highest temperature region appeared in permanent magnets no matter the PMWG was connected to pure resistance load or rectifier load.

According to Fig. (11), when the generator was connected to resistance load, because the eddy current loss in permanent magnet was relatively small (3.08W), the PMWG temperature relatively lower. The highest temperature was 51.3°C.

However, when the generator was connected to rectifier, because the permanent magnet eddy current loss was increased (39.8W), the temperature significantly rises and the highest temperature increased by 26.7°C, which means, it was increased by 52%. So, the rectifier greatly raised the permanent magnet temperature and reduced the performance of permanent magnet excitation.

PMWG armature winding temperature was affected by the armature copper loss, and the armature copper loss was affected by the output current. Because the increased output current caused the increased copper loss when the generator was connected to rectifier load, the temperature of the stator winding raised from 53.5°C to 63.2°C. The rectifier also raised the stator slot winding temperature.

In order to verify the accuracy of the temperature field analysis, and further study the temperature field at the same time, the temperature experiment data of PMWG was obtained when it was connected to different load respectively. The surface temperature of the rotor and stator winding was tested. Fig. (12) shows the temperature test results.

Because the prototype had a large capacity margin, when it runs at the condition of 8kW, the whole temperature field distribution is relatively low. But the generator temperature distributions of different parts have the coincidence with the simulation results. So, it still could verify the above results.

When the PMWG was connected to rectifier load, the generator casing surface temperature was significantly higher than the temperature when it was connected to resistance load. Highest casing temperature was beyond 6°C. The above conclusions were consistent with the results of temperature field analysis, which verified the nonlinear rectifier load effectively improved the temperature.

Fig. (12) The test data of the temperature distribution.

To sum up, the rectifier had significance influence on generator temperature, especially on permanent magnets. The performance of permanent magnet excitation was reduced.

Taking an 8kW 2000 r/min PMWG as an example, based on the principle of the field-circuit coupling, this research analyzed the influence of pure resistance load and rectifier load on the electromagnetic and temperature fields. Some conclusions are obtained as follows:

1. The output line voltage harmonic and current harmonic were increased when the PMWG was connected to rectifier. After a fantastic harmonic decomposition, the output line voltage and current harmonics ((2k+1)^th, k=1,2,3,...) were increased. The line voltage THD was increased from 1.5% to 25.3%, the current THD was increased from 5.5% to 9.4% when the generator was connected to rectifier.
2. When the PMWG was connected to the rectifier load, the biggest eddy current density was increased to. It was 1.42 times when the generator was connected to resistance load. The increased eddy current density caused the eddy current loss raised 9.4 times. Because the influence of armature reaction, the stator core loss was decreased by 10.1%, and the armature winding copper loss was increased by 6.69%.
3. The rectifier load raised the line voltage and current non-sinusoidal degree, and increased the harmonic and eddy current loss. Because the nonlinear circuit PF was affected by the current THD, the increased current THD made PF reduced from 1 to 0.99. The generator performance became worse.
4. Affected by the influence of the loss, the rectifier raised whole generator temperature. Especially it raised the permanent magnet temperature. The performance of permanent magnet excitation was reduced. When the rectifier loads were connected to the generator, permanent magnet temperature raised by 52%, the temperature of the stator winding raised by 19.4%. When the temperature rose to a certain extent, it was easy to cause the excitation-loss fault.