- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Electrical & Electronic Engineering Journal
(Discontinued)
ISSN: 1874-1290 ― Volume 13, 2019
Stability Analysis for Stochastic Markovian Jumping Neural Networks with Leakage Delay
Yajun Li1, *, Xisheng Dai2, Wenping Xiao1, Like Jiao1
Abstract
The stability problem for a class of stochastic neural networks with Markovian jump parameters and leakage delay is addressed in this study. The sufficient condition to ensure an exponentially stable stochastic neural networks system is presented and proven with Lyapunov functional theory, stochastic stability technique and linear matrix inequality method. The effect of leakage delay on the stability of the neural networks system is discussed and numerical examples are provided to show the correctness and effectiveness of the research results .
Article Information
Identifiers and Pagination:
Year: 2017Volume: 11
First Page: 1
Last Page: 13
Publisher Id: TOEEJ-11-1
DOI: 10.2174/1874129001711010001
Article History:
Received Date: 15/01/2016Revision Received Date: 31/08/2016
Acceptance Date: 01/09/2016
Electronic publication date: 25/01/2017
Collection year: 2016
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
* Address correspondence to this author at Shunde Polytechnic, Desheng East Road, Shunde District, Foshan City, Guangdong province, 528300, China; Tel: 13420841579; Fax: 0757-22322669; E-mail: lyjfirst@163.com, 5380901@qq.com
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 15-01-2016 |
Original Manuscript | Stability Analysis for Stochastic Markovian Jumping Neural Networks with Leakage Delay | |
1. INTRODUCTION
In the past decades, neural networks systems have elicited much attention because of its massive potential application in many fields, such as pattern classification, reconstruction of moving images, and combinatorial optimization, etc. In the real applications, ensuring the stability of the equilibrium point of the designed neural networks is an important task and has been a popular topic. Time delay and stochastic disturbance are well known as the two main factors that affect the stability of neural networks. Many new results have been obtained from stability analyses of stochastic neural networks with different types of time delays [1S. Arik, "Global asymptotic stability of a larger class of neural networks with constant time delay", Phys. Lett., Sec. A, vol. 311, no. 6, pp. 504-511, 2003.
[http://dx.doi.org/10.1016/S0375-9601(03)00569-3] -8R. Yang, H. Gao, and P. Shi, "Novel robust stability criteria for stochastic Hopfield neural networks with time delays", IEEE Trans. Syst. Man Cybern. B Cybern., vol. 39, no. 2, pp. 467-474, 2009.
[http://dx.doi.org/10.1109/TSMCB.2008.2006860] [PMID: 19095547] ].
Recently, a special delay called leakage or forgetting delay has been investigated widely since its existence in real systems was discovered. This special delay affects the stability of time delay systems. Many exciting research results have been reported recently [9K. Gopalsamy, "Leakage delays in BAM", J. Math. Anal. Appl., vol. 325, no. 2, pp. 1117-1132, 2007.
[http://dx.doi.org/10.1016/j.jmaa.2006.02.039] -13M. Park, O. Kwon, J. Park, S. Lee, and E. Cha, "Synchronization criteria for coupled stochastic neural networks with time-varying delays and leakage delay", J. Franklin Inst., vol. 349, no. 5, pp. 1699-1720, 2012.
[http://dx.doi.org/10.1016/j.jfranklin.2012.02.002] ]. As pointed out in [9K. Gopalsamy, "Leakage delays in BAM", J. Math. Anal. Appl., vol. 325, no. 2, pp. 1117-1132, 2007.
[http://dx.doi.org/10.1016/j.jmaa.2006.02.039] , 10Q. Song, and Z. Zhao, "Stability criterion of complex-valued neural networks with both leakage delay and time-varying delays on time scales", Neurocomputing, vol. 171, no. 3, pp. 179-184, 2016.], neural networks with leakage delay is a class of important networks. In [10Q. Song, and Z. Zhao, "Stability criterion of complex-valued neural networks with both leakage delay and time-varying delays on time scales", Neurocomputing, vol. 171, no. 3, pp. 179-184, 2016.], the global exponential stability of complex-valued neural networks with leakage delay was investigated with complex-valued linear matrix inequality technique, by establishing a novel stability lemma . Then, by using stochastic analysis theory and matrix inequalities technique, the exponential stability of a kind of stochastic neural networks with leakage terms are studied in [11W. Xie, Q. Zhu, and F. Jiang, "Exponential stability of stochastic neural networks with leakage delays and expectations in the coefficients", Neurocomputing, vol. 173, no. 3, pp. 1268-1275, 2016.
[http://dx.doi.org/10.1016/j.neucom.2015.08.086] ]. The global μ-stability results for complex-valued neural networks with leakage time delay and unbounded time-varying delays were obtained in [12P. Balasubramaniam, M. Kalpana, and R. Rakkiyappan, "Global asymptotic stability of BAM fuzzy cellular neural networks with time delay in the leakage term", Math. Comput. Model., vol. 53, no. 5-6, pp. 839-853, 2011.
[http://dx.doi.org/10.1016/j.mcm.2010.10.021] ] through the free weighting matrix method and stability theory. By using the properties of M-matrix, the properties of the fuzzy logic operator, the eigenvalue of the spectral radius of nonnegative matrices and delay differential inequality, a class of fuzzy cellular neural networks with time delay in the leakage term and impulsive perturbations was investigated in [13M. Park, O. Kwon, J. Park, S. Lee, and E. Cha, "Synchronization criteria for coupled stochastic neural networks with time-varying delays and leakage delay", J. Franklin Inst., vol. 349, no. 5, pp. 1699-1720, 2012.
[http://dx.doi.org/10.1016/j.jfranklin.2012.02.002] ]. However, the leakage delay studied above was constant. Subsequently, the research on leakage delay was extended to time-varying [14P. Balasubramaniam, V. Vembarasan, and R. Rakkiyappan, "Leakage delays in T-S fuzzy cellular neural networks", Neural Process. Lett., vol. 33, no. 2, pp. 111-136, 2011.
[http://dx.doi.org/10.1007/s11063-010-9168-3] , 15Q. Song, and J. Cao, "Passivity of uncertain neural networks with both leakage delay and time-varying delay", Nonlinear Dyn., vol. 67, no. 2, pp. 1695-1707, 2012.
[http://dx.doi.org/10.1007/s11071-011-0097-0] ]. In [14P. Balasubramaniam, V. Vembarasan, and R. Rakkiyappan, "Leakage delays in T-S fuzzy cellular neural networks", Neural Process. Lett., vol. 33, no. 2, pp. 111-136, 2011.
[http://dx.doi.org/10.1007/s11063-010-9168-3] ], with Lyapunov method, a triple Lyapunov-Krasovskii functional term was employed to study the robust stability of discrete-time uncertain neural networks with leakage time-varying delay.
Stochastic model plays an important role in the branches of economics, industry and science. A particular field of interest is stochastic system with Markovian jumping parameters. The Markovian jump system shows an advantage in modeling these dynamic systems presented above, and much progress has been made in stability analysis, impulsive response and state estimation of stochastic neural networks with Markovian jumping parameters, [16Z. Wang, Y. Liu, M. Li, and X. Liu, "Stability analysis for stochastic Cohen-Grossberg neural networks with mixed time delays", IEEE Trans. Neural Netw., vol. 17, no. 3, pp. 814-820, 2006.
[http://dx.doi.org/10.1109/TNN.2006.872355] [PMID: 16722186] -23Q. Zhu, and J. Cao, "Robust exponential stability of Markovian jump impulsive stochastic Cohen-Grossberg neural networks with mixed time delays", IEEE Trans. Neural Netw., vol. 21, no. 8, pp. 1314-1325, 2010.
[http://dx.doi.org/10.1109/TNN.2010.2054108] [PMID: 20639177] ] and references therein.
Motivated by the discussion above, this study investigates the exponential stability of a class of stochastic neural networks with time-varying and leakage delays. By employing a suitable Lyapunov functional and introducing a new inequality technique, the sufficient condition to render the system exponentially stable is obtained by solving a set of strict linear matrix inequalities. Examples and simulations are presented to show the effectiveness of the proposed methods. The mutual effect between discrete and leakage delays as well as the derivative of time-delay are discussed. The experimental analysis reveals that the effect of leakage delay existing in neural networks on stability can not be disregarded.
2. PROBLEM FORMULATION
Let rt, t ≥ 0 be a right-continuous Markov chain defined on a complete probability space (Ω,F,P) and take discrete values in a finite state space S = {1, 2, ..., N} with generator given by Π = (πij)N×N:
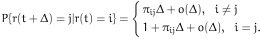 |
(1) |
where Δ > 0, πij ≥ 0 is the transition rate from i to j while
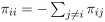 .
.
Consider the following stochastic neural network with time-varying delay:
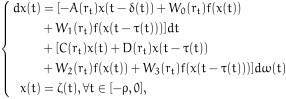 |
(2) |
where
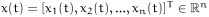 is the state vector of the neural network associated with n neurons, ω(t) is an m-dimensional Brownian motion defined on a probability space (Ω,F,P), which is assumed to satisfy E{dω(t)} = 0, E{dω2(t)} = dt. A(rt) = diag{a1,...,an} is a diagonal matrix with positive entries ai > 0 (i = 1, 2,..., n), f(x(t)) = [f(x1(t)),..., f(xn(t))]T
is the state vector of the neural network associated with n neurons, ω(t) is an m-dimensional Brownian motion defined on a probability space (Ω,F,P), which is assumed to satisfy E{dω(t)} = 0, E{dω2(t)} = dt. A(rt) = diag{a1,...,an} is a diagonal matrix with positive entries ai > 0 (i = 1, 2,..., n), f(x(t)) = [f(x1(t)),..., f(xn(t))]T
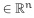 denotes the neuron activation function and W0(rt), W1(rt), W2(rt), W3(rt) are the connection weight matrices and the delayed connection weight matrices, respectively. C(rt) and D(rt) are known real constant matrices with compatible dimensions. The δ(t), τ(t) denotes leakage term and the transmission delay, respectively, which satisfying:
denotes the neuron activation function and W0(rt), W1(rt), W2(rt), W3(rt) are the connection weight matrices and the delayed connection weight matrices, respectively. C(rt) and D(rt) are known real constant matrices with compatible dimensions. The δ(t), τ(t) denotes leakage term and the transmission delay, respectively, which satisfying:
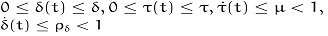 |
(3) |
ρ = max{δ, τ} and µ is some positive scalar. ζ(t) is real-valued continuous initial condition on [-ρ, 0]. Throughout the paper, we assume that ω(t) and r(t) are independent.
For simplicity, in the sequel, for each rt = i ϵ S, A(rt), W0(rt), W1(rt) are denoted by Ai, W0i, W1i and so on. Therefore, the system (2) can be rewritten as:
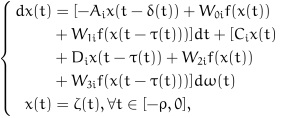 |
(4) |
Assumption 1. For i ϵ {1,2,..., n},
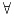 x, y,
x, y,
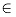 ,
,
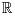 , x ≠ y, the neuron activation function fi(·) is continuous, bounded and satisfies:
, x ≠ y, the neuron activation function fi(·) is continuous, bounded and satisfies:
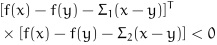 |
(5) |
where Σ1 and Σ2 are some constant matrices.
Remark 1. In this study, Assumption 1 is based on neuron activation function, which is called sector-bounded neuron activation function [12P. Balasubramaniam, M. Kalpana, and R. Rakkiyappan, "Global asymptotic stability of BAM fuzzy cellular neural networks with time delay in the leakage term", Math. Comput. Model., vol. 53, no. 5-6, pp. 839-853, 2011.
[http://dx.doi.org/10.1016/j.mcm.2010.10.021] ]. As pointed out in [12P. Balasubramaniam, M. Kalpana, and R. Rakkiyappan, "Global asymptotic stability of BAM fuzzy cellular neural networks with time delay in the leakage term", Math. Comput. Model., vol. 53, no. 5-6, pp. 839-853, 2011.
[http://dx.doi.org/10.1016/j.mcm.2010.10.021] ], when Σ1 = Σ2 = -Σ, the condition (5) becomes:
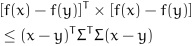 |
(6) |
The condition is less restrictive than the descriptions on both the sigmond activation functions [9K. Gopalsamy, "Leakage delays in BAM", J. Math. Anal. Appl., vol. 325, no. 2, pp. 1117-1132, 2007.
[http://dx.doi.org/10.1016/j.jmaa.2006.02.039] , 10Q. Song, and Z. Zhao, "Stability criterion of complex-valued neural networks with both leakage delay and time-varying delays on time scales", Neurocomputing, vol. 171, no. 3, pp. 179-184, 2016.] and the Lipschitz-type activation functions.
At first, we derive the following Lemmas which will be used frequently in the proof of our main results.
Lemma 1 [4T. Li, and X.L. Ye, "Improved stability criteria of neural networks with time-varying delays: An augmented LKF approach", Neurocomputing, vol. 73, no. 4-6, pp. 1038-1047, 2010.
[http://dx.doi.org/10.1016/j.neucom.2009.10.001] ]. For any constant symmetric positive defined matrix J
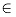 Rm×m, scalar η and the vector function ν : [0, η]→
Rm×m, scalar η and the vector function ν : [0, η]→
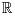 m, the following inequality holds:
m, the following inequality holds:
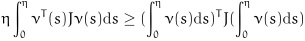
Lemma 2 [24H. Wu, J. Wang, and P. Shi, "A delay decomposition approach to L2-L1 filter design for stochastic systems with time-varying delay", Automatica, vol. 47, no. 7, pp. 1482-1488, 2011.
[http://dx.doi.org/10.1016/j.automatica.2011.02.021] ]. Assume that x(t), φ(t), g(t) satisfy the stochastic differential equation
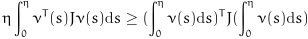 |
(7) |
where ω(t) is a Brownian motion. For any constant matrix Z ≥ 0 and scalar h > 0, the following integration holds:
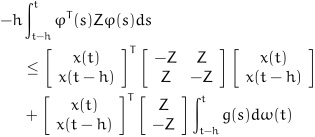 |
(8) |
Definition 1. The stochastic neural networks system (2) is said to be exponential stable in the mean square sense, if there exist positive scalars α, β such that:
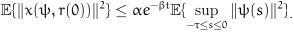 |
(9) |
3. MAIN RESULTS
In this section, the exponential stability of system (4) is developed by Theorem 1.
Theorem 1. For given positive scalars δ, µ, ρσ and τ, the Markovian jumping stochastic neural network system (4) is exponential mean square stable, if there exist symmetric positive definite matrices Pi, i
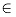 S, Rk(k = 1,2,3,4,5) and two diagonal matrices F1 > 0, F2 > 0 such that the following linear matrix inequality (LMI) holds:
S, Rk(k = 1,2,3,4,5) and two diagonal matrices F1 > 0, F2 > 0 such that the following linear matrix inequality (LMI) holds:
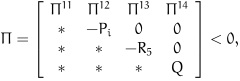 |
(10) |
where
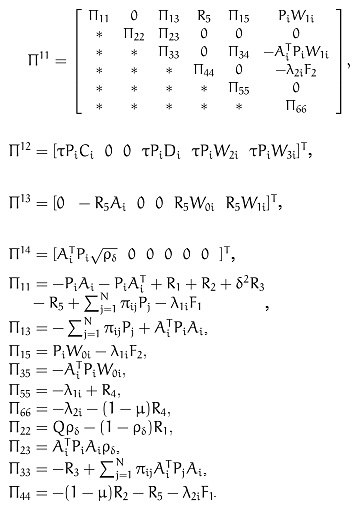
Proof: For simplicity, we let:
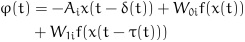 |
(11) |
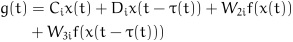 |
(12) |
Then the system (4) can be rewritten as:
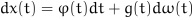 |
(13) |
We choose the following Lyapunov-Krasovskii functional candidate as:
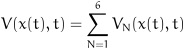 |
(14) |
where
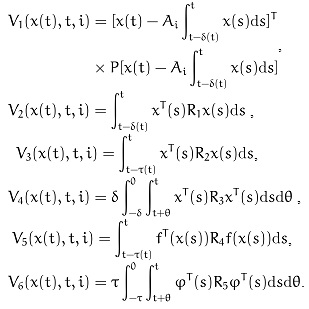
Following Itô differential rule, the stochastic differential of dѴ(x(t), t, i) with respect to t along the system (4) is obtained by:
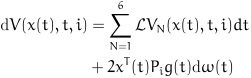 |
(15) |
where
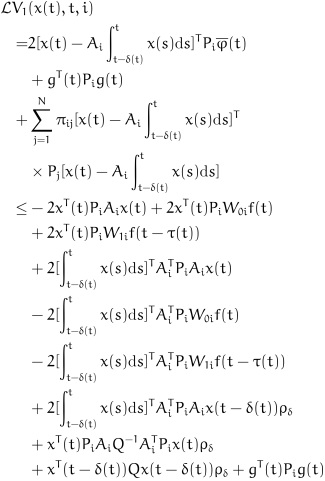 |
(16) |
and
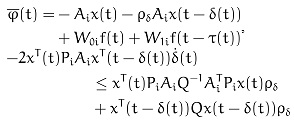
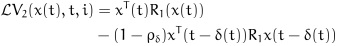 |
(17) |
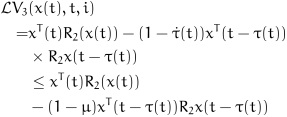 |
(18) |
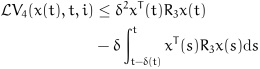 |
(19) |
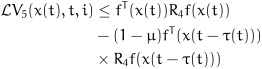 |
(20) |
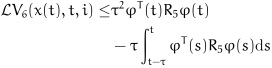 |
(21) |
Applying Lemma 1 to (19) and Lemma 2 to (21), we can obtain:
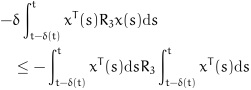 |
(22) |
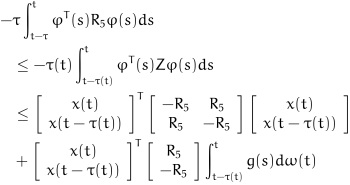 |
(23) |
On the other hand, it can be deduced from Assumption 1 that for i = 1,2,..., n,
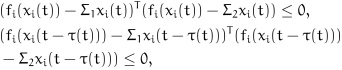 |
(24) |
Then there exist scalars λ1i > 0, λ2i > 0, diagonal matrices F1 ≥ 0, F2 ≥ 0 and Σi(i = 1, 2) such that the following inequalities hold:
 |
(25) |
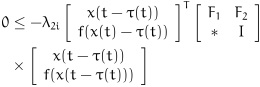 |
(26) |
where
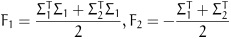 |
(27) |
By substituting (16)-(23) into (15), and adding the right sides of (25)-(26) to the right side of (15), we can obtain:
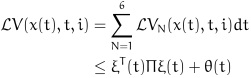 |
(28) |
where Π = Π11 + Π12 Pi-1 (Π12)T + Π13 R5-1 (Π13)T,
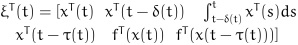 .
.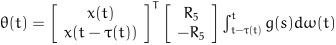 .
.By taking expectations on both sides of (28), we can obtain:
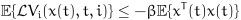 |
(29) |
where
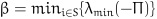 .
.Then, by taking expectations on both side of (16) and integrating from 0 to T, we can obtain:
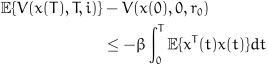 |
(30) |
At the same time, it follows from (14) that:
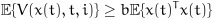 |
(31) |
where
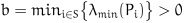 .
.Therefore, from (30)-(31), the following inequality can be obtained:
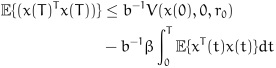 |
(32) |
Applying Gronwall-Bellman lemma to the inequality (30), we can obtain:
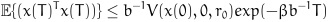 .
.Noting that there exists a scalar α > 0 such that:
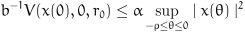 |
(33) |
Then by (9), we can draw the conclusion that the system (4) is exponentially mean square stable, thus completing the proof.
When leakage delay is constant, that is, δ(t) = δ, the system (4) can be rewritten as follows:
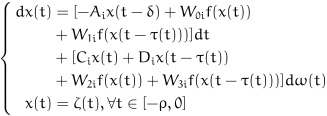 |
(34) |
Then we can get the following Theorem 2:
Theorem 2. For given positive scalars δ, µ and τ, the Markovian jumping stochastic neural network system (34) is exponential mean square stable, if there exist symmetric positive definite matrices Pi, Rj(j = 1,2,3,4,5) and two diagonal matrices F1 > 0, F2 > 0 such that the following linear matrix inequality (LMI) holds:
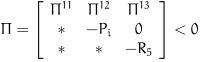 ,
,where
 ,
,4. NUMERICAL EXAMPLES
In this section, two numerical examples with simulation results are provided to demonstrate the effectiveness of the proposed approaches.
Example 1. Consider a two-neuron stochastic neural networks system (4) with the following parameters:
Mode 1
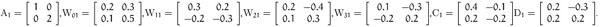
Mode 2
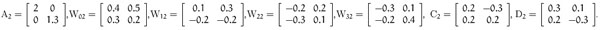
Assume that the Markov process governing the mode switching generates:
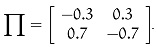
Take the neuron activation functions as follows: f (x) = 0.5(|x + 1| - |x - 1|).
Following Assumption 1, we obtain, F1 = diag {0, 0}, F2 = diag {0.05, 0.05}. In this example, we set µ = 0.3, τ = 0.8 and δ = 0.26, by virtue of the Matlab LMI Control box, solving the LMI (10), the feasible solution can be obtained as follows:
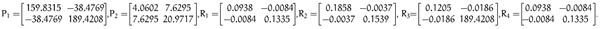
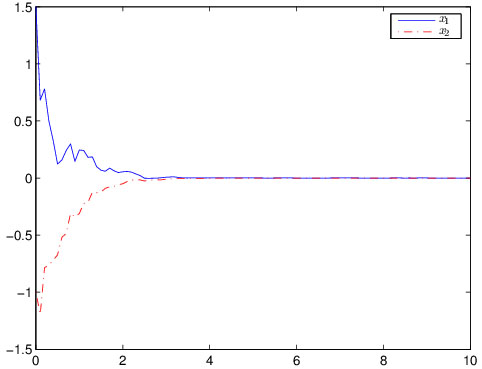 |
Fig. (1) Response of the state x(t). |
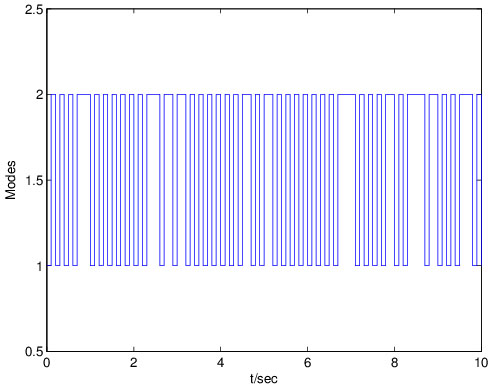 |
Fig. (2) Markovian jumping mode of x(t). |
The simulation results of the state response of system (4) are plotted in Figs. (1 ) and (2
) and (2 ), where the initial condition x(0) = [1.5; -1], Fig. (1
), where the initial condition x(0) = [1.5; -1], Fig. (1 ) shows the state response of system (4), and Fig. (2
) shows the state response of system (4), and Fig. (2 ) depicts the switching modes. The figures illustrate that when two Markov processes are under control, the stochastic neural networks system with leakage delay is stable.
) depicts the switching modes. The figures illustrate that when two Markov processes are under control, the stochastic neural networks system with leakage delay is stable.
The upper bounds of delays ρσ, δ and τ guaranteeing the stability of system (4) are listed from Tables 1 to 3, where - signifies that LMI (10) exhibits no feasible solution. Table 1 shows the maximum allowable upper bound δ for different values of ρσ, which indicating that the bound of the derivative of the leakage time-varying is effective and plays an important role in obtaining feasible results.
Table 2 indicates that when fixing the value of ε, ρσ and γ, the allowable upper value of τ is effected by δ, especially when δ = 0.2, the feasible solution cannot be obtained.
When ρσ is a non-zero constant, the allowable upper bounds of τ for different values of ε are listed in Table 3.
Example 2. Consider a three-neuron two-mode stochastic neural networks with Markovian jump parameters and mixed time delays (2) with the following parameters:
Mode 1
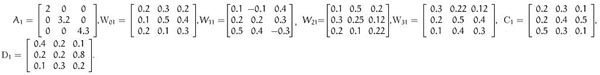
Mode 2
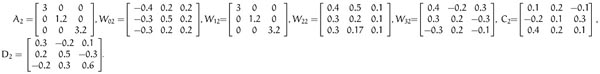
Let the Markov process governing the mode switching has generator:
By setting µ = 0.1, ρσ = 0.001, τ = 1.2 the state and switching modes simulation curve of the system (4) are shown in Figs. (3 ) and (4
) and (4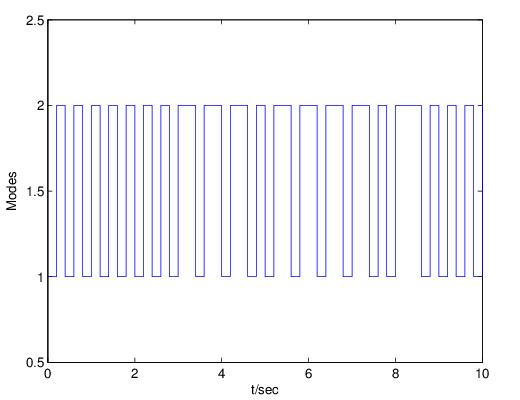 ), which conform the effectiveness of our results.
), which conform the effectiveness of our results.
 |
Fig. (3) Response of the state x(t). |
 |
Fig. (4) Markovian jumping mode of x(t). |
Furthermore, by setting δ = 0.8 and τ = 1.6, we can obtain the state simulation curve in Fig. (5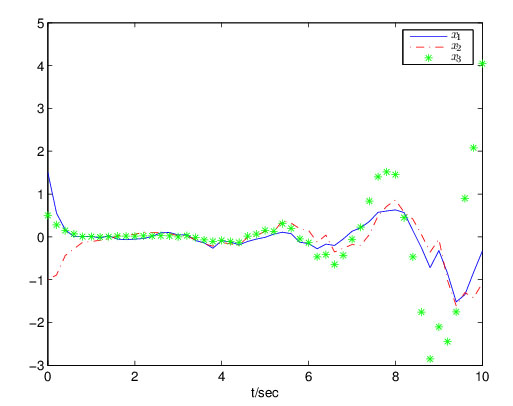 ). Fig. (5
). Fig. (5 ) indicates that when leakage delay increases, the system (4) tends to be unstable.
) indicates that when leakage delay increases, the system (4) tends to be unstable.
 |
Fig. (5) Response of the state x(t). |
SUMMARY
We studied the stability problem for a class of stochastic neural networks with Markovian jump parameters and leakage delay in this study. By employing a proper Lyapunov functional, combined with the stochastic stability analysis method, the stability criterion is derived to ensure the developed system is exponentially mean square stable based on LMIs. Finally, we discussed the effect of leakage delay on stability of neural networks system. Numerical examples were provided to testify the rightness and effectiveness of the research results.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
The authors are very much thankful to the editor and anonymous reviewers for their careful reading, constructive comments and fruitful suggestions to improve the quality of this manuscript. This work was supported by the Natural Science Foundation of Guang Dong Province under grants 2015A030310336 and the National Natural Science Foundation of No. 61364006.
REFERENCES
| [1] | S. Arik, "Global asymptotic stability of a larger class of neural networks with constant time delay", Phys. Lett., Sec. A, vol. 311, no. 6, pp. 504-511, 2003. [http://dx.doi.org/10.1016/S0375-9601(03)00569-3] |
| [2] | Y. He, G. Liu, D. Rees, and M. Wu, "Stability analysis for neural networks with time-varying interval delay", IEEE Trans. Neural Netw., vol. 18, no. 6, pp. 1850-1854, 2007. [http://dx.doi.org/10.1109/TNN.2007.903147] |
| [3] | C. Song, H. Gao, and W. Zheng, "A new approach to stability analysis of discrete-time recurrent neural networks with time-varying delay", Neurocomputing, vol. 72, no. 10-12, pp. 2563-2568, 2009. [http://dx.doi.org/10.1016/j.neucom.2008.11.009] |
| [4] | T. Li, and X.L. Ye, "Improved stability criteria of neural networks with time-varying delays: An augmented LKF approach", Neurocomputing, vol. 73, no. 4-6, pp. 1038-1047, 2010. [http://dx.doi.org/10.1016/j.neucom.2009.10.001] |
| [5] | W.H. Chen, X. Lu, Z.H. Guan, and W.X. Zheng, "Delay-dependent exponential stability of neural networks with variable delay: An LMI approach", IEEE Trans. Circuits Sys. II, vol. 53, no. 9, pp. 837-842, 2006. [http://dx.doi.org/10.1109/TCSII.2006.881824] |
| [6] | H.B. Zeng, Y. He, M. Wu, and C.F. Zhang, "Complete delay-decomposing approach to asymptotic stability for neural networks with time-varying delays", IEEE Trans. Neural Netw., vol. 22, no. 5, pp. 806-812, 2011. [http://dx.doi.org/10.1109/TNN.2011.2111383] [PMID: 21421436] |
| [7] | L. Hu, H. Gao, and P. Shi, "New stability criteria for Cohen-Grossberg neural networks with time delays", IET Control Theory Appl., vol. 3, no. 9, pp. 1275-1282, 2009. [http://dx.doi.org/10.1049/iet-cta.2008.0213] |
| [8] | R. Yang, H. Gao, and P. Shi, "Novel robust stability criteria for stochastic Hopfield neural networks with time delays", IEEE Trans. Syst. Man Cybern. B Cybern., vol. 39, no. 2, pp. 467-474, 2009. [http://dx.doi.org/10.1109/TSMCB.2008.2006860] [PMID: 19095547] |
| [9] | K. Gopalsamy, "Leakage delays in BAM", J. Math. Anal. Appl., vol. 325, no. 2, pp. 1117-1132, 2007. [http://dx.doi.org/10.1016/j.jmaa.2006.02.039] |
| [10] | Q. Song, and Z. Zhao, "Stability criterion of complex-valued neural networks with both leakage delay and time-varying delays on time scales", Neurocomputing, vol. 171, no. 3, pp. 179-184, 2016. |
| [11] | W. Xie, Q. Zhu, and F. Jiang, "Exponential stability of stochastic neural networks with leakage delays and expectations in the coefficients", Neurocomputing, vol. 173, no. 3, pp. 1268-1275, 2016. [http://dx.doi.org/10.1016/j.neucom.2015.08.086] |
| [12] | P. Balasubramaniam, M. Kalpana, and R. Rakkiyappan, "Global asymptotic stability of BAM fuzzy cellular neural networks with time delay in the leakage term", Math. Comput. Model., vol. 53, no. 5-6, pp. 839-853, 2011. [http://dx.doi.org/10.1016/j.mcm.2010.10.021] |
| [13] | M. Park, O. Kwon, J. Park, S. Lee, and E. Cha, "Synchronization criteria for coupled stochastic neural networks with time-varying delays and leakage delay", J. Franklin Inst., vol. 349, no. 5, pp. 1699-1720, 2012. [http://dx.doi.org/10.1016/j.jfranklin.2012.02.002] |
| [14] | P. Balasubramaniam, V. Vembarasan, and R. Rakkiyappan, "Leakage delays in T-S fuzzy cellular neural networks", Neural Process. Lett., vol. 33, no. 2, pp. 111-136, 2011. [http://dx.doi.org/10.1007/s11063-010-9168-3] |
| [15] | Q. Song, and J. Cao, "Passivity of uncertain neural networks with both leakage delay and time-varying delay", Nonlinear Dyn., vol. 67, no. 2, pp. 1695-1707, 2012. [http://dx.doi.org/10.1007/s11071-011-0097-0] |
| [16] | Z. Wang, Y. Liu, M. Li, and X. Liu, "Stability analysis for stochastic Cohen-Grossberg neural networks with mixed time delays", IEEE Trans. Neural Netw., vol. 17, no. 3, pp. 814-820, 2006. [http://dx.doi.org/10.1109/TNN.2006.872355] [PMID: 16722186] |
| [17] | J. Hu, S. Zhong, and L. Liang, "Exponential stability analysis of stochastic delayed cellular neural network", Chaos Solitons Fractals, vol. 27, no. 4, pp. 1006-1010, 2006. [http://dx.doi.org/10.1016/j.chaos.2005.04.067] |
| [18] | R. Rakkiyappan, P. Balasubramaniam, and S. Lakshmanan, "Robust stability results for uncertain stochastic neural networks with discrete interval and distributed time-varying delays", Phys. Lett. A, vol. 372, no. 32, pp. 5290-5298, 2008. [http://dx.doi.org/10.1016/j.physleta.2008.06.011] |
| [19] | Z. Wang, J. Fang, and X. Liu, "Global stability of stochastic high-order neural networks with discrete and distributed delays", Chaos Solitons Fractals, vol. 36, no. 2, pp. 388-396, 2008. [http://dx.doi.org/10.1016/j.chaos.2006.06.063] |
| [20] | X. Lou, and B. Cui, "Stochastic exponential stability for Markovian jumping BAM neural networks with time-varying delays", IEEE Trans. Syst. Man Cybern. B Cybern., vol. 37, no. 3, pp. 713-719, 2007. [http://dx.doi.org/10.1109/TSMCB.2006.887426] [PMID: 17550124] |
| [21] | Q. Ma, S. Xu, Y. Zou, and J. Lu, "Stability of stochastic Markovian jump neural networks with mode-dependent delays", Neurocomputing, vol. 74, no. 12–13, pp. 2157-2163, 2011. [http://dx.doi.org/10.1016/j.neucom.2011.01.016] |
| [22] | Y. Chen, and W.X. Zheng, "Stochastic state estimation for neural networks with distributed delays and Markovian jump", Neural Netw., vol. 25, no. 1, pp. 14-20, 2012. [http://dx.doi.org/10.1016/j.neunet.2011.08.002] [PMID: 21899985] |
| [23] | Q. Zhu, and J. Cao, "Robust exponential stability of Markovian jump impulsive stochastic Cohen-Grossberg neural networks with mixed time delays", IEEE Trans. Neural Netw., vol. 21, no. 8, pp. 1314-1325, 2010. [http://dx.doi.org/10.1109/TNN.2010.2054108] [PMID: 20639177] |
| [24] | H. Wu, J. Wang, and P. Shi, "A delay decomposition approach to L2-L1 filter design for stochastic systems with time-varying delay", Automatica, vol. 47, no. 7, pp. 1482-1488, 2011. [http://dx.doi.org/10.1016/j.automatica.2011.02.021] |






