- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Electrical & Electronic Engineering Journal
(Discontinued)
ISSN: 1874-1290 ― Volume 13, 2019
Implementation of the Predictive Current Control of Multi-Pulse Flexible Topology Thyristor Rectifier Under Unbalanced Source Voltages
Zhang Damin1, *, Wang Shitao2, Kang Shaobo1, Zhang Ji1
Abstract
Predictive current control strategy has captured much concern recently in power converters. As for the multi-pulse flexible-topology thyristor rectifiers (m-PFTTR), the symmetry of the input line-to-line voltages has great influence upon the implementation of the control strategy. Existing literatures have mainly focused on the implementation under ideal condition, i.e., the input line-to-line voltages, being critical to the predictive current controller, were supposed to be symmetrical. In fact, the unbalance of the input line-to-line voltages usually exists in the windings of the zigzag transformer at front end and the A/D converter of the digital signal processor (DSP). This paper presents a new method to dynamically regulate the input line-to-line voltages to ensure the symmetry of each other. It is realized through the instantaneous correction of the bias values in the course of sampling, and the correction is embodied in the modified control algorithm. The paper includes analyses of the m-PFTTR as well as the control algorithm, simulation and experiments. Simulation and experimental results demonstrate the effectiveness of the presented method.
Article Information
Identifiers and Pagination:
Year: 2017Volume: 11
First Page: 14
Last Page: 22
Publisher Id: TOEEJ-11-14
DOI: 10.2174/1874129001711010014
Article History:
Received Date: 05/05/2016Revision Received Date: 14/11/2016
Acceptance Date: 08/12/2016
Electronic publication date: 25/01/2017
Collection year: 2017
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
* Address correspondence to this author at the Xiamen University of Technology, No.600, Ligong Road, Jimei, Xiamen, China; Tel: +8615659283976; E-mail: hqxmzj@sina.com
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 05-05-2016 |
Original Manuscript | Implementation of the Predictive Current Control of Multi-Pulse Flexible Topology Thyristor Rectifier Under Unbalanced Source Voltages | |
1. INTRODUCTION
Predictive current control has recently drawn considerable attention due to the rapid development of the digital processors. It has been demonstrated to be particularly useful for power converters with multitudinous and complicated control challenges [1P. Cortes, J. Rodriguez, C. Silva, and A. Flores, "Delay compensation in model predictive current control of a three-phase inverter", IEEE Transactions on Industrial Electronics, vol. 59, pp. 1323-1325, 2012.]. In predictive control strategy, a cost function is usually introduced to mark different performances and non-linear constraints. Fast response, simple conception and easy implementation are the main advantages which are the reason of popularity among researchers. It can be found in a variety of literatures such as motor drives, inverters and converters, which are all concerned with power electronics [2H. Youn, J. Park, K. Park, J. Baek, and G. Moon, "A digital predictive peak current control for power factor correction with low-input current distortion", IEEE Transactions on Power Electronics, vol. 31, pp. 900-912, 2016.
[http://dx.doi.org/10.1109/TPEL.2015.2417194] -10Z. Song, Y. Tian, W. Chen, Z. Zou, and Z. Chen, "Predictive duty cycle control of three-phase active-front-end rectifiers", IEEE Transactions on Power Electronics, vol. 31, pp. 698-710, 2016.
[http://dx.doi.org/10.1109/TPEL.2015.2398872] ]. Being attracted by the adaptiveness in the PWM converters, the predictive current control strategy was also employed in thyristor rectifier by Jun-Keun et al. [11J. Jun-Keun, and S. Seung-Ki, "Operation analysis and new current control of parallel connected dual converter system without interphase reactors", Industrial Electronics Society, vol. 1, pp. 235-240, 1999.
[http://dx.doi.org/10.1109/IECON.1999.822202] ]. A 12-pulse thyristor rectifier which consisted of two 6-pulse rectifiers in parallel was studied. Fast current response was achieved by predicting the firing angles with the information of load current, input and output voltages of present instant. However, Newton-Raphson or other complex numerical methods were required to solve the firing angle which was embedded in two complex non-linear transcendental equations. To free from solving the complex non-linear equation, a simple predictive current control strategy was proposed to a six-pulse thyristor rectifier with generator-type load whose terminal voltage varied slowly [12S. Srdic, and M. Nedeljkovic, "Predictive fast DSP-based current controller for thyristor converters", IEEE Transactions on Industrial Electronics, vol. 58, pp. 3349-3358, 2011.]. It has been shown that the numerical calculations of the firing angles were left out and replaced by a calculation of voltage-time area of the DC-side inductor. Input and output voltages as well as load current were measured and sent to DSP to calculate the firing moments instead of firing angles. Therefore, the algorithm presented in paper [12S. Srdic, and M. Nedeljkovic, "Predictive fast DSP-based current controller for thyristor converters", IEEE Transactions on Industrial Electronics, vol. 58, pp. 3349-3358, 2011.] was insensitive to the variation of the load parameters.
It is well known that the six-pulse thyristor rectifier usually causes problem with regard to power quality, particularly when it feeds light loads. This problem can be alleviated to some extent by extending to 12-pulse flexible-topology thyristor rectifier or 18-pulse flexible-topology counterpart [13D. Zhang, S. Wang, H. Lin, and Z. Lu, "Predictive current control of multi-pulse flexible-topology thyristor AC-DC converter", Journal of Zhejiang University Science, vol. 14, pp. 296-310, 2013.
[http://dx.doi.org/10.1631/jzus.C1200283] , 14Z. Damin, W. Shitao, Z. Fengwu, W. Lujun, and L. Zhengyu, "Predictive fast DSP-based current controller for a 12-pulse hybrid-mode thyristor rectifier", IEEE Transactions on Power Electronics, vol. 28, pp. 5263-5271, 2013.], both for the sake of mitigating the harmonic pollution and improving the power factor. Specifically, the multi-pulse (12- or more) flexible-topology thyristor rectifier was composed of several six-pulse thyristor rectifiers with the same structures. It had two operating modes which were shifted by several auxiliary switches. The predictive current control was employed to obtain fast current response and smooth switching between the two operating modes. It is noted that the implementation of the predictive current control in actual conditions such as unbalanced line-to-line voltages and the failure of the DC-side inductor were not taken into account in those aforementioned literatures. The control algorithm conducted in all of the three literatures above was under completely idealized conditions. Namely, the input multi-phase AC voltages generated by a zigzag transformer were supposed to be strictly symmetrical. While in general, it is difficult to obtain absolutely symmetrical AC voltages from the outputs of the zigzag transformer due to its complicated construction and different technics of the windings. What’s more, the sampled values of the input AC voltages might lose its symmetry after the modulation of a particular DC circuit with bias values being superposed on. It was observed that the unbalance seems to be unavoidable even if the input AC voltages were symmetrical.
Since the asymmetry of the input AC voltages is an essential problem to the implementation of the predictive current control algorithm, it is necessary to analyze the effect that the unbalanced voltages take upon to the control strategy. Hence, this paper discusses the control algorithm under unbalance voltages and attempts to improve the performance of control algorithm.
2. INTRODUCTION TO THE m-PFTTR
A brief introduction to the m-PFTTR is indispensable for the upcoming statement of the predictive current control strategy under unbalanced voltages. A 12-PFTTR is employed in this paper to expound the topology and operating principle thereof. The elaborated description of the 12-PFTTR is carried out in [14Z. Damin, W. Shitao, Z. Fengwu, W. Lujun, and L. Zhengyu, "Predictive fast DSP-based current controller for a 12-pulse hybrid-mode thyristor rectifier", IEEE Transactions on Power Electronics, vol. 28, pp. 5263-5271, 2013.] where a detailed analysis of the structure and working modes along with the control algorithm was developed. A schematic of the 12-PFTTR is shown in Fig. (1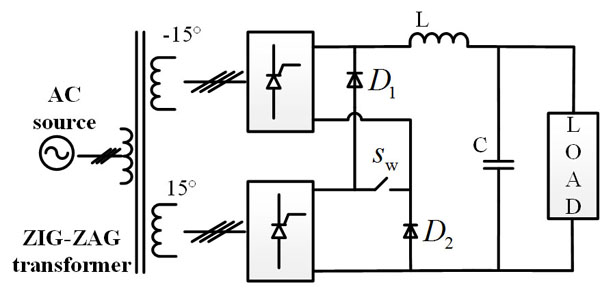 ) where it consists of two conventional six-pulse thyristor rectifiers with an auxiliary switch and two extra diodes. An IGBT or GTO can be used as a switch for the transitions between two operating modes. The series mode will emerge when the switch is turned on and the parallel mode will appear as soon as the switch is turned off.
) where it consists of two conventional six-pulse thyristor rectifiers with an auxiliary switch and two extra diodes. An IGBT or GTO can be used as a switch for the transitions between two operating modes. The series mode will emerge when the switch is turned on and the parallel mode will appear as soon as the switch is turned off.
 |
Fig. (1) Schematic of the 12-PFTTR. |
The predictive current control algorithm, instead of conventional PI control, has been used in the 12-PFTTR to gain fast current response. The block diagram of the control algorithm is shown in Fig. (2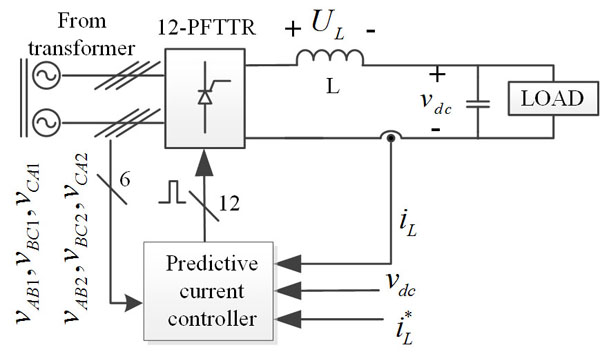 ). It has been demonstrated through the simulation and experimental results that both the dynamic current response and transitions between the two modes are fast and smooth, providing that the input signals to the predictive current controller are balanced, without any difference in the magnitude of voltages or phases [14Z. Damin, W. Shitao, Z. Fengwu, W. Lujun, and L. Zhengyu, "Predictive fast DSP-based current controller for a 12-pulse hybrid-mode thyristor rectifier", IEEE Transactions on Power Electronics, vol. 28, pp. 5263-5271, 2013.]. The input line-to-line voltages, the terminal voltage of the load, the load current and the reference current are all the input signals to the predictive current controller. The controller calculates the predicted current based on these input signals and compares it with the given reference current via a cost function. The conduction sequence of the thyristors is then applied to optimize the cost function and the one minimize the cost function is reserved. Finally, the firing signals are generated and send to the proper pair of thyristors which were determined based on the aforementioned input signals and conduction sequence.
). It has been demonstrated through the simulation and experimental results that both the dynamic current response and transitions between the two modes are fast and smooth, providing that the input signals to the predictive current controller are balanced, without any difference in the magnitude of voltages or phases [14Z. Damin, W. Shitao, Z. Fengwu, W. Lujun, and L. Zhengyu, "Predictive fast DSP-based current controller for a 12-pulse hybrid-mode thyristor rectifier", IEEE Transactions on Power Electronics, vol. 28, pp. 5263-5271, 2013.]. The input line-to-line voltages, the terminal voltage of the load, the load current and the reference current are all the input signals to the predictive current controller. The controller calculates the predicted current based on these input signals and compares it with the given reference current via a cost function. The conduction sequence of the thyristors is then applied to optimize the cost function and the one minimize the cost function is reserved. Finally, the firing signals are generated and send to the proper pair of thyristors which were determined based on the aforementioned input signals and conduction sequence.
 |
Fig. (2) Block diagram of the predictive current control algorithm. |
3. ANALYSIS OF THE CONTROL ALGORITHM UNDER UNBALANCED INPUT VOLTAGES
3.1. Introduction of the Predictive Current Control Strategy.
In this section, a brief introduction to the predictive current control algorithm is developed, the detailed description of the control algorithm can be referred in [14Z. Damin, W. Shitao, Z. Fengwu, W. Lujun, and L. Zhengyu, "Predictive fast DSP-based current controller for a 12-pulse hybrid-mode thyristor rectifier", IEEE Transactions on Power Electronics, vol. 28, pp. 5263-5271, 2013.]. It is based on the fact that the current of the load at instant t1 can be predicted by the current at instant tO and the calculation of the voltage-time area between the instants tO and t1, this is shown in Fig. (3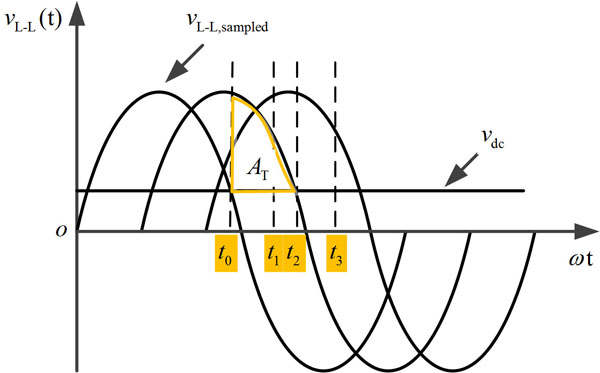 ) and equation (1).
) and equation (1).
 |
Fig. (3) Illustration of the predictive current control strategy: |
 |
(1) |
Define a temporary variable AT and let:
 |
(2) |
Accordingly, the equation (1) is rewritten as:
 |
(3) |
Likewise, the load current at instant t3 is predicted with the given information of iL(t2) and voltage-time integral between the intervals [t2,t3]. Then the temporary variable can be written as:
 |
(4) |
and:
 |
(5) |
According to the previous discussion, it is obvious that the temporary variable AT is not a constant. It depends on the voltage-time integral and the terminal voltage of the DC-side inductor, as can be seen from equation (4). Thus, the essential idea of the predictive current control is to calculate AT and sample the current value of iL(tO) instantaneously. The terminal voltage of the DC-side inductor is rewritten as:
 |
(6) |
where vL-L represents the line-to-line voltages from the output windings of the zigzag transformer. Then the available current increment ∆iL(t) of the DC-side inductor is deduced hereunder:
 |
(7) |
where 
∆iL(t) achieves its maximal value ∆iLmax when AT is integrated from t2 to t3. Then the current increment of the DC-side inductor at instant t2 is followed:
 |
(8) |
Then the firing instants of the proper thyristors are determined when and only when the sum of the instantaneous current iL(t) value and the predicted current increment ∆iL(t) equals to the given reference current i*L. In this way, the predictive current control is achieved:
 |
(9) |
3.2. Analysis of Unbalanced Line-to-Line Voltages to the Predictive Current Control Strategy
According to the previous description, the effectiveness of the predictive current control depends very closely on the accuracy of input line-to-line voltages and terminal voltages of the inductor and load, respectively. Any inaccuracy of these parameters may leads to an error between practical and reference current. Moreover, the current error will accumulate if the inaccuracy of the parameters is not corrected in every period.
In addition, the course of the digitalization of the line-to-line voltages, the instantaneous current and the terminal voltage of the load are all the cause of inaccurate prediction of the practical load current. Generally, the analog to digital (A/D) converter of the digital signal processor (DSP) only receives and sends signals with the form of DC component. Thus, the original AC signals from resistances or Hall sensors are required to superpose a DC component before sending to the A/D converter of the DSP, which means the values of the signals are greater than zero in the whole time. The original signals are separated from the superposed ones in the DSP by removing the DC component which is also called biases. An appropriate bias value has great relation with the precision of the sampling resistances, the value fluctuation of the voltage source for the signal modulating circuits and the offset currents of the Hall sensors. And the voltages biases finally influence the calculations of the voltage-time areas which play vital roles in executing the control algorithm. For example, a datasheet of some Hall sensor reports that it may have an offset current of 6% when operating in nominal condition, which means that a bigger offset current occurs if the sensor isn’t powered by a rated voltage source.
As far as it is concerned, no literature has concentrated on the problem. The reason for considering this issue is that the performance of the control algorithm has greatly suffered from the drifting of the bias values. Motivated by the above contributions, this paper presents a new method to dynamically regulate the bias values of the line-to-line voltages, which guarantee the sampled input voltages against unbalance. The real-time dynamic adjustment of the bias values is embedded in the control algorithm which is executed by a DSP controller. As can be seen from equation (7), if there exists an error or a drifting of the bias value, it will be accumulated and augmented after a few cycles of integral (see the second term of the equation (7)). The values of the voltage-time area at every sinusoidal half-wave voltage will not equal to each other, and finally lead to the failure of the algorithm:
 |
(10) |
Therefore, it is indispensable to correct the bias values instantaneously in order to guarantee the balance of the sampled line-to-line voltages. The area comparison, based on the same sampling times in positive half-cycle and negative half-cycle, are used to estimate the symmetry of the sampled line-to-line voltages. The direction to dynamical adjustment of the bias value will be determined as soon as the area comparison is finished. As shown in Fig. (4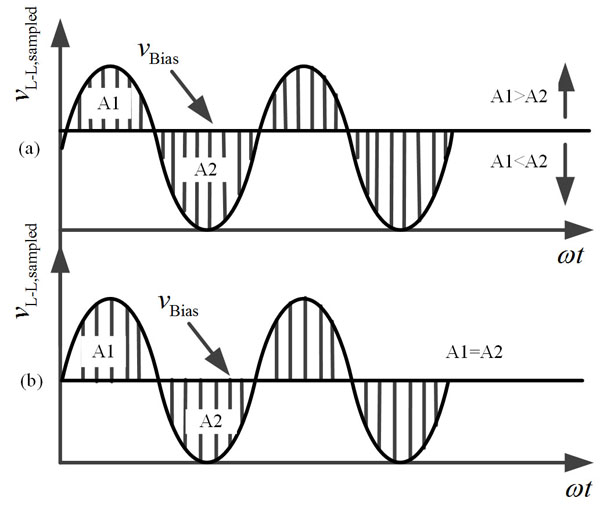 ), if the positive half-cycle area is larger than that of the negative half-cycle, the bias value will be adjusted downwards. On the contrary, the bias value will be regulated upwards. Fig. (4a
), if the positive half-cycle area is larger than that of the negative half-cycle, the bias value will be adjusted downwards. On the contrary, the bias value will be regulated upwards. Fig. (4a ) shows the dynamic process of regulating the bias value and Fig. (4b
) shows the dynamic process of regulating the bias value and Fig. (4b ) describes the final line-to-line voltages after dynamic adjustment with the method proposed in the paper.
) describes the final line-to-line voltages after dynamic adjustment with the method proposed in the paper.
 |
Fig. (4) Instantaneous correction of the sampling bias of line-to-line voltage. |
The proposed method is also capable of coping with the problem of unbalance of the line-to-line voltages supplied by secondary windings of the zigzag transformer. In this case, the voltage-time areas of the three-phase line-to-line voltages need to calculate respectively and then compare with each other to check unbalanced ones. Subsequently, several independent variables which stand for different biases are introduced in the dynamic adjustments of the positive- and negative-half-cycle areas, as shown in Fig. (5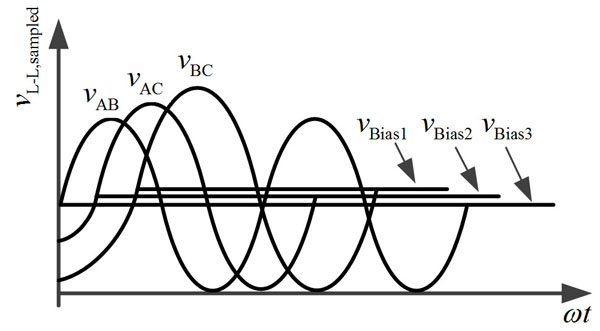 ). In this way, the sampled line-to-line voltages have been balanced before involving in the control algorithm.
). In this way, the sampled line-to-line voltages have been balanced before involving in the control algorithm.
 |
Fig. (5) Different bias values used for unbalanced line-to-line voltages. |
4. SIMULATION AND EXPERIMENTAL VERIFICATION
Based on the previous analyses, a simulation model along with its corresponding laboratory prototype of the 12pFTTR is set up to validate the effectiveness of the proposed method. TMS320F2812 digital controller is employed to carry out the predictive current control algorithm. Fig. (6 ) shows a part of the laboratory prototype, and a programmable AC/DC electronic load and a bulky zig-zag transformer are not included. Table 1 gives the experimental setup specifications.
) shows a part of the laboratory prototype, and a programmable AC/DC electronic load and a bulky zig-zag transformer are not included. Table 1 gives the experimental setup specifications.
 |
Fig. (6) Experimental setup of 12-PFTTR. |
Simulation results corresponding to unbalanced and balanced input line-to-line voltages are displayed in Figs. (7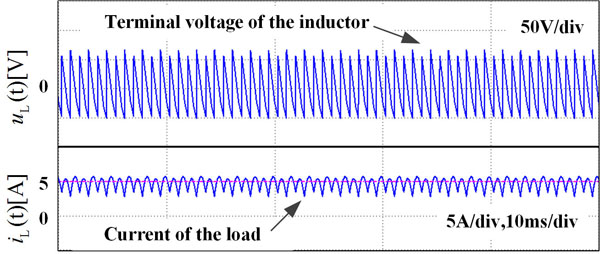 and 8
and 8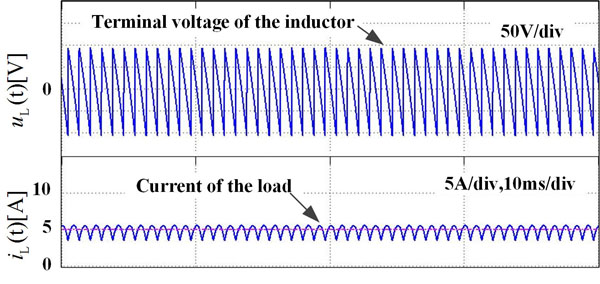 ) where the former is generated by setting the outputs of the zigzag transformer of winding 1 being lower than winding 2 with 5%. It is observed that the load current is not symmetrical due to the unbalanced line-to-line voltages. The load current returns to be symmetrical with the proposed correcting method, as can be seen in Fig. (8
) where the former is generated by setting the outputs of the zigzag transformer of winding 1 being lower than winding 2 with 5%. It is observed that the load current is not symmetrical due to the unbalanced line-to-line voltages. The load current returns to be symmetrical with the proposed correcting method, as can be seen in Fig. (8 ). As the simulation result with the proposed method is nearly same as that of the balanced line-to-line voltages, current response with proposed method is also shown in Fig. (8
). As the simulation result with the proposed method is nearly same as that of the balanced line-to-line voltages, current response with proposed method is also shown in Fig. (8 ).
).
 |
Fig. (7) Current response under unbalanced line-to-line voltages (simulation). |
 |
Fig. (8) Current response of line-to-line voltages after corrected (simulation). |
In experiment, the bias value is chosen in this way. First, an approximate value is acquired by calculating the peak-peak value of the sampled signals, as shown in Fig. (4a ). Then, the precise bias value is gained by instantaneously adjusting the zero line to make sure the voltage-time areas of positive part equals negative part. As shown in Fig. (4b
). Then, the precise bias value is gained by instantaneously adjusting the zero line to make sure the voltage-time areas of positive part equals negative part. As shown in Fig. (4b ) where A1 is equal to A2.
) where A1 is equal to A2.
Experimental result about unbalanced line-to-line voltages is shown in Fig. (9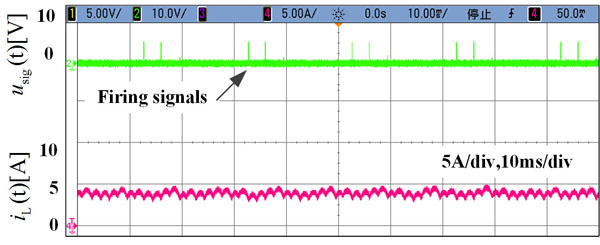 ) where the line-to-line voltages provided by the zigzag transformer are unbalanced. The firing signals generated by the unmodified control algorithm are also exhibited in the figure. The asymmetry of the line-to-line voltages has an effect upon the calculation of the voltage-time area, which eventually affects the precision of the predicted current. Steady-state current response with proposed correcting method is shown in Fig. (10
) where the line-to-line voltages provided by the zigzag transformer are unbalanced. The firing signals generated by the unmodified control algorithm are also exhibited in the figure. The asymmetry of the line-to-line voltages has an effect upon the calculation of the voltage-time area, which eventually affects the precision of the predicted current. Steady-state current response with proposed correcting method is shown in Fig. (10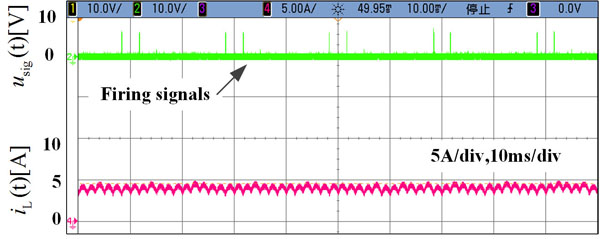 ). As compared to Fig. (9
). As compared to Fig. (9 ), the asymmetry of the load current is improved obviously with the proposed correcting method, indicating that the modified control algorithm is capable of fast response with the unbalanced voltages.
), the asymmetry of the load current is improved obviously with the proposed correcting method, indicating that the modified control algorithm is capable of fast response with the unbalanced voltages.
 |
Fig. (9) Current response under unbalanced line-to-line voltages. |
 |
Fig. (10) Current response with proposed correcting method. |
CONCLUSION
This paper presents a new method to cope with the unbalances of the sampled line-to-line voltages with regard to predictive current control algorithm. To expressly address this issue, a brief introduction to 12-PFTTR as well as control strategy is developed, and then discussions about the control algorithm under unbalanced voltages are carried out. Based on the analyses above, a modified control algorithm is used for 12-PFTTR for unbalanced scenario. A simulation model and its corresponding experimental setup are constructed to verify the validity of the presented method. Both the simulation and experimental results have shown that the modified control algorithm applied in the 12-PFTTR deals well with the unbalanced voltages.
Although the presented method is only verified in 12-PFTTR, it is easy to be extended to m-PFTTR (m ≥ 18) in the same way. This is particularly useful in high power applications, and the stability of the control algorithm will be further strengthened.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
The authors thank Referees and Editors for valuable comments and helpful suggestions.
Project supported in part by the National Natural Science Foundation of China (Grant No. 51407151) and in part by the Natural Science Foundation of Fujian Province, China (Grant No. 2015J05113).
REFERENCES
| [1] | P. Cortes, J. Rodriguez, C. Silva, and A. Flores, "Delay compensation in model predictive current control of a three-phase inverter", IEEE Transactions on Industrial Electronics, vol. 59, pp. 1323-1325, 2012. |
| [2] | H. Youn, J. Park, K. Park, J. Baek, and G. Moon, "A digital predictive peak current control for power factor correction with low-input current distortion", IEEE Transactions on Power Electronics, vol. 31, pp. 900-912, 2016. [http://dx.doi.org/10.1109/TPEL.2015.2417194] |
| [3] | H. Guzman, M.J. Duran, F. Barrero, L. Zarri, B. Bogado, I. Gonzalez Prieto, and M.R. Arahal, "Comparative study of predictive and resonant controllers in fault-tolerant five-phase induction motor drives", IEEE Transactions on Industrial Electronics, vol. 63, pp. 606-617, 2016. [http://dx.doi.org/10.1109/TIE.2015.2418732] |
| [4] | W. Song, J. Ma, L. Zhou, and X. Feng, "Deadbeat predictive power control of single-phase three-level neutral-point-clamped converters using space-vector modulation for electric railway traction", IEEE Transactions on Power Electronics, vol. 31, pp. 721-732, 2016. [http://dx.doi.org/10.1109/TPEL.2015.2400924] |
| [5] | T. Turker, U. Buyukkeles, and A. Bakan, "A robust predictive current controller for PMSM drives", IEEE Transactions on Industrial Electronics, vol. 63, pp. 3904-3914, 2016. [http://dx.doi.org/10.1109/TIE.2016.2521338] |
| [6] | A. Calle-Prado, S. Alepuz, J. Bordonau, J. Nicolas-Apruzzese, P. Cortes, and J. Rodriguez, "Model predictive current control of grid-connected neutral-point-clamped converters to meet low-voltage ride-through requirements", IEEE Transactions on Industrial Electronics, vol. 62, pp. 1503-1514, 2015. [http://dx.doi.org/10.1109/TIE.2014.2364459] |
| [7] | X. Li, and P. Shamsi, "Inductance surface learning for model predictive current control of switched reluctance motors", IEEE Transactions on Transportation Electrification, vol. 1, pp. 287-297, 2015. [http://dx.doi.org/10.1109/TTE.2015.2468178] |
| [8] | A. Darba, F. De Belie, P. D'haese, and J.A. Melkebeek, "Improved dynamic behavior in BLDC drives using model predictive speed and current control", IEEE Transactions on Industrial Electronics, vol. 63, pp. 728-740, 2016. [http://dx.doi.org/10.1109/TIE.2015.2477262] |
| [9] | C. Lin, J. Yu, Y. Lai, H. Yu, Y. Lin, and F. Chen, "Simplified model-free predictive current control for interior permanent magnet synchronous motors", Electronics Letters, vol. 52, pp. 49-50, 2016. [http://dx.doi.org/10.1049/el.2015.2372] |
| [10] | Z. Song, Y. Tian, W. Chen, Z. Zou, and Z. Chen, "Predictive duty cycle control of three-phase active-front-end rectifiers", IEEE Transactions on Power Electronics, vol. 31, pp. 698-710, 2016. [http://dx.doi.org/10.1109/TPEL.2015.2398872] |
| [11] | J. Jun-Keun, and S. Seung-Ki, "Operation analysis and new current control of parallel connected dual converter system without interphase reactors", Industrial Electronics Society, vol. 1, pp. 235-240, 1999. [http://dx.doi.org/10.1109/IECON.1999.822202] |
| [12] | S. Srdic, and M. Nedeljkovic, "Predictive fast DSP-based current controller for thyristor converters", IEEE Transactions on Industrial Electronics, vol. 58, pp. 3349-3358, 2011. |
| [13] | D. Zhang, S. Wang, H. Lin, and Z. Lu, "Predictive current control of multi-pulse flexible-topology thyristor AC-DC converter", Journal of Zhejiang University Science, vol. 14, pp. 296-310, 2013. [http://dx.doi.org/10.1631/jzus.C1200283] |
| [14] | Z. Damin, W. Shitao, Z. Fengwu, W. Lujun, and L. Zhengyu, "Predictive fast DSP-based current controller for a 12-pulse hybrid-mode thyristor rectifier", IEEE Transactions on Power Electronics, vol. 28, pp. 5263-5271, 2013. |




