The Open Electrical & Electronic Engineering Journal




(Discontinued)

ISSN: 1874-1290 ― Volume 13, 2019
RESEARCH ARTICLE

Hybrid Active-Passive Robust Fault-Tolerant Control of Event-Triggered Nonlinear NCS



Jun Wang*, Xiaowan Yao, Wei Li
College of Electrical and Information Engineering, Lanzhou University of Technology, Peoples Republic of China

Abstract

In this paper, the authors aimed to analyze uncertain nonlinear networked control systems (NCS) under discrete event-triggered communication scheme (DETCS), in which an integrated design methodology between robust fault detection observer and active fault-tolerant controller is proposed. Moreover, the problem of hybrid active–passive robust fault-tolerant control, which integrated passive fault-tolerant control, fault detection, and controller reconstruction, is researched. In consideration of the impact of uncertainties and network-induced delay on system performance, a new class of uncertain nonlinear NCS fault model is established based on T-S fuzzy model. By employing Lyapunov stability theory, H∞ control theory, and linear matrix inequality method, the fault detection observer and hybrid fault-tolerant controller are both appropriately designed. In addition, the sufficient condition that guaranteed the asymptotically robust stability of nonlinear NCS against any actuator failures is deduced. Finally, a numerical simulation is provided to show the effectiveness of the proposed methods.

Keywords: Nonlinear networked control system, Hybrid active–passive robust fault-tolerant control, T-S fuzzy model, Discrete event-triggered communication scheme, Fault detection, PTTCS.

Article Information


Identifiers and Pagination:

Year: 2017
Volume: 11
First Page: 68
Last Page: 86
Publisher Id: TOEEJ-11-68
DOI: 10.2174/1874129001711010068

Article History:

Received Date: 16/07/2016
Revision Received Date: 21/11/2016
Acceptance Date: 01/12/2016
Electronic publication date: 28/02/2017
Collection year: 2017

© 2017 Wang et al.

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.


* Address correspondence to this author at College of Electrical and Information Engineering, Lanzhou University of Technology, Peoples Republic of China; Tel: 1500260 8239; E-mail: wangj31901@163.com



1. INTRODUCTION

The faster development of the modern industry and the complexity in structural design of nonlinear networked control systems (NCS) have led to increased possibility of system faults. A fault-tolerant controller (FTC) is capable of ensuring the stability of the system as well as keeping the performance of the system at an acceptable level. FTC can be achieved either passively by using the off-line designed passive fault-tolerant controller (PFTC) that is robust to predictable failures of the system [1L. Huolong, A Study on Design of Passive Fault-tolerant Control System Based on LMI Approach., Northeastern University, 2010.] or actively by using the real-time online fault detection observer (FDO) and controller reconstruction to tolerant unknown faults [2Q. Shen, B. Jiang, P. Shi, and C.C. Lim, "Novel neural networks-based fault tolerant control scheme with fault alarm", IEEE Transactions on Cybernetics, vol. 44, no. 11, pp. 2190-2201, 2014.
[http://dx.doi.org/10.1109/TCYB.2014.2303131] [PMID: 25014982] , 3H. Huang, X.D. Han, D.X. Xie, and Z.Q. Wang, "Active fault-tolerant control for networked control systems with packet dropout", Control and Decision, vol. 24, no. 8, pp. 1126-1131, 2009.]. However, these two above mentioned methods have disadvantages. A new idea named hybrid active–passive fault-tolerant control, which combined the merits of these two methods, is rarely reported up to now. Most of the researches on FTC for NCS still adopt the period time-triggered communication scheme (PTTCS), whereas the combination between NCS and the discrete event-triggered communication scheme (DETCS), a more efficient way to save network resources, requires further study [4H. Songlin, Analysis and Synthesis of Networked Control Systems with Event-Triggering Scheme., Huazhong University of Science & Technology, 2012.]. The only document that could be referred is [5W. Jun, L. Shuzhen, and L. Wei, "Design of hybrid fault-tolerant networked control system based on event-triggered scheme", Journal of Shanghai Institute of Technology, vol. 15, no. 2, pp. 178-184, 2015. [Natural Science].], which aimed at independent event generator and researched hybrid active–passive fault-tolerant control problem of NCS. Although it has simplified design progress, it still has limitation to the economy of networked resources.

Over the recent years, the model-based approach of fault detection aimed at NCS has received significant attention [6Y. Wang, Y. Sun, C. Chang, and Y. Hu, Model-Based Fault Detection and Fault Tolerant Control of SCR Urea Injection System., Vehicular Technology, 2015., 7M.K. Seyed, S. Karim, and J.Y. Mohamad, "Multiple model-based fault detection and diagnosis for nonlinear model predictive fault-tolerant control", Arabian Journal for Science and Engineering, vol. 39, no. 10, pp. 7433-7442, 2014.
[http://dx.doi.org/10.1007/s13369-014-1252-y] ]. However, links between fault detection and FTC are still deficient. Although some recent results on the integration of fault detection and FTC can be found [8H.R. Karimi, M. Chadli, S. Peng, and Z. Lixian, "Fault detection, isolation, and tolerant control of vehicles using soft computing methods", IET Control Theory & Applications, vol. 8, no. 9, pp. 655-657, 2014.
[http://dx.doi.org/10.1049/iet-cta.2014.0577] , 9M. Mongi, B.A. Hechmi, F. Khaled, J. Mohamed, and B. Mohamed, "Fault detection and fault-tolerant control of power converter fed PMSM", Electrical Engineering, vol. 98, no. 2, pp. 121-131, 2016.
[http://dx.doi.org/10.1007/s00202-015-0350-5] ], not much are applied to NCS. Therefore, the integration of FDO and hybrid fault-tolerant controller for nonlinear NCS (NNCS) is attracting more and more attention recently. Among all classes of possible faults, actuator fault is considered to be the most easily occurring. On the contrary, most literature, which related actuator fault-tolerant control, only addresses linear plants [10M.M. Seron, J.A. De Dona, and J.H. Richter, "Integrated sensor and actuator fault-tolerant control", International Journal of Control, vol. 86, no. 4, pp. 689-708, 2013.
[http://dx.doi.org/10.1080/00207179.2012.757653] ]. Most actual systems are nonlinear by nature or at least have nonlinear characteristics [11Hy. Cho, S.M. Fei, D. Yue, C. Peng, and J.T. Sun, "Quantized control for nonlinear networked control systems", Fuzzy Sets and Systems, vol. 1174, pp. 99-113, 2011.
[http://dx.doi.org/10.1016/j.fss.2011.01.011] , 13M. Takahashi, and T. Takagi, "Adaptive fault-tolerant control based on hybrid redundancy", Asia-Pacific Journal of Chemical Engineering, vol. 7, no. 5, pp. 642-650, 2012.
[http://dx.doi.org/10.1002/apj.1628] ]. T-S fuzzy model could express nonlinear model as fuzzy fusion of many partial linear models by using fuzzy rules; therefore, it has attracted extensive attention worldwide in the recent years, and many significant problems about it have been deeply researched and has made great progress [14L. Jinliang, Z. Gu, and F. Shumin, "Reliable control for nonlinear systems with stochastic actuators fault and random delays through a T-S fuzzy model approach", Acta Mathematicae Applicatae Sinica, vol. 32, no. 2, pp. 395-406, 2016.
[http://dx.doi.org/10.1007/s10255-016-0566-9] , 17H. Li, L. Wu, J. Li, F. Sun, and Y. Xia, "Stabilization and Separation Principle of Networked Control Systems Using the T–S Fuzzy Model Approach", IEEE Transactions on Fuzzy Systems, vol. 23, no. 5, pp. 1832-1843, 2015.
[http://dx.doi.org/10.1109/TFUZZ.2014.2382131] ]. Reference [18W. Jun, L. Wei, and G. Ling, "Fuzzy observer-based robust guaranteed cost fault-tolerant design for nonlinear NCS", Open Electrical and Electronic Engineering Journal, vol. 8, no. 1, pp. 71-76, 2014.
[http://dx.doi.org/10.2174/1874129001408010071] ] only applied passive fault-tolerant techniques to solve the problem of robust guaranteed cost fault-tolerant control for NNCS with network-induced delay and packed dropout. To the author’s knowledge, up to now, no report exists about hybrid active–passive robust fault-tolerant control for NNCS based on T-S fuzzy model.

According to the aforementioned analysis, the present paper has researched the controller design problem of hybrid active–passive robust fault-tolerant control for uncertain NNCS against any actuator failure by using appropriately constructed Lyapunov function, H∞ control theory, and linear matrix inequality (LMI) method, so that the system could realize the following functions: under the premise of saving network resources as much as possible, when known faults appear, PFTC would be tolerant to system faults and maintains stability; when unknown faults appear, PFTC could slow down the rate of system performance deterioration for the sake of FDO that needs time to detect faults; once accurate fault information is detected, the controller will be reconstructed immediately so that the influence of faults could be compensated, and the system could resiliently be stable as soon as possible.

2. MATERIAL AND METHODS

2.1. The Description of NNCS Model

Consider an uncertain NNCS described by the T-S fuzzy model, where the ith rule of it is expressed as follows:

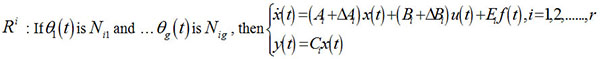where r is the number of rules; x(t) ϵ Rn is the state vector; u(t) ϵ Rm, y(t) ϵ Rp represents the input and output vector of the system, respectively; Nis = (s = 1,2, ...g) is the fuzzy set; θ(t) = [θ1(t), θ2(t), θg(t)]T denotes the premise variables and assumes that it does not rely on u (t); and f(t) ϵ Rr is the signal of actuator faults, assuming f(t) is an additional fault that satisfied 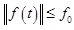. When no fault happens, the value is 0, and it will change into a time-varying form or a definite value when faults appear. Ai, Bi, Ci, Ei (i = 1,2...r) are constant matrices with appropriate dimensions; ΔAi, ΔBi denote the uncertainty of system parameter and assumed as norm-bounded. They are time-varying, and described as

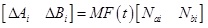(1)

where M, Nai and Nbi are constant matrices with suitable dimensions, respectively; F (t) is an unknown time-varying function matrix whose elements are Lebesgue measurable and satisfies FT (t)F (t) ≤ 1.

The following T-S fuzzy system state equation can be inferred by using center-average defuzzifier, product inference, and singleton fuzzifier:

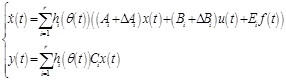(2)

where 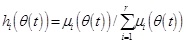, , 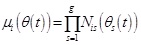and Nis (θs (t)) are the membership value of (θs(t)) in Nis. Suppose µi (θ(t)≥ 0(i = 1,2,...r) and 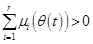, then hi (θ(t)≥ 0 as well as .

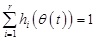2.2. The Introduction of DETCS

For NNCS, DETCS means an introduction of communication constraint condition. Whether or not the sampled state should be transmitted is determined by the current-sampled state and the state error in sampled period. Only when the event-triggered condition is satisfied, then the data will be transmitted, and vice versa. This will make the system save more network resources under the circumstances of keeping the corresponding expected performance, and therefore increase the efficiency of network utilization.

The structure of the hybrid active–passive fault-tolerant control of NNCS under DETCS is shown in Fig. (1).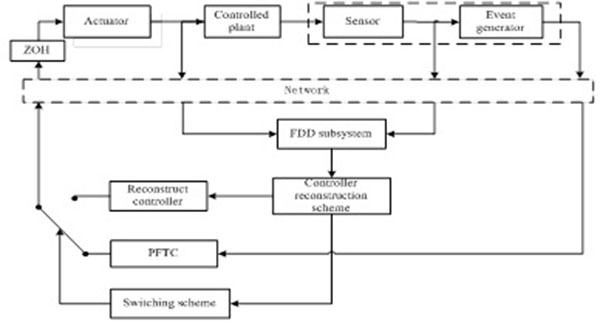

For case of convenient exposition, the following assumptions are made:

Assumption 1. Sensors are clock-driven, and controllers and actuators are event-driven. The system states are sampled at a constant period; h, ik, h is represented for sampled instants; and the set of sampled instants is represented by .

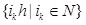Assumption 2. The transmitted instants tkh are determined by the sampled states x(ikh). The set of transmission instants is represented by 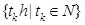, which is a subset of .

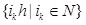Assumption 3. The state of the system is completely measured, and it adopts state-feedback control strategy. The delays at transmitted instants tk h are lumped together as 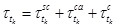, where, τt1sc, τt1ca and τt1ca represent the delays from the sensor to the controller, from the controller to the actuator, and computational delays, respectively.

Assumption 4. The detection of fault information is beyond the influence of event-triggered condition, that is, fault information can be transmitted to fault detection observer at every sampled instant.

Assumption 5. The role of the zero order holder (ZOH) is to store the latest data packet. Thus, the actuator keeps the control input unchanged until the output of the ZOH is updated to a new value.

Fig. (1)
Structure of the system.


Compared with traditional NCS, the sample data need to pass the event generator before being transmitted by the network, as depicted in Fig. (1), and its function is to determine whether or not to transmit the latest sample signal to the controller. We adopt the following event-triggered condition [19L. Wei, and Y. Kun, "Integrity design of uncertainty nonlinear networked control system based on discrete event-triggered scheme", Journal of Lanzhou University of Technology, vol. 41, no. 2, pp. 83-90, 2015.]:

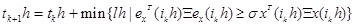(3)

where

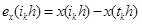(4)

h is the sampling period, Ξ is a symmetric positive definite matrix, and σ is the bounded positive scalar.

Not all the sampled data could be transmitted; only when x(ikh) and x(tkh) satisfied the event-triggered condition (3) will the event generator be triggered and data x(ikh) be transmitted. If the event-triggered condition is designed properly, then the use of DETCS will help the system save more network resources as well as increase the efficiency of resource utilization on the basis of ensuring the system performance at an acceptable level.

2.3. NNCS Fault Model Based on DETCS

From Assumption 3, we can get the truth that the state of the system is completely measurable. Based on the previous description of the controlled plant (2), the feedback controller is designed and the ith rule of the state-feedback control can be described as

Ri: If θ1(t) is Ni1 and...θg(t) … is, Nigthen

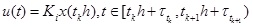
where Ki (i = 1,2,...r) represent controller gain matrices to be determined in the following theorem; andare network-induced delay at the transmitting instant tkh and tk+1h, respectively.

Meanwhile, considering the role of ZOH when, 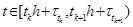the state-feedback control law, according to the PDC algorithm, is shown as follows:

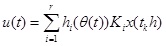(5)

Define

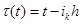(6)

Obviously, τ (t) is a continuous linear function that meets the requirement of 0 < τm≤ τ (t) ≤ τM; where τm and τM are the lower and upper bounds of network-induced delay, respectively. Define τs = τM - τM.

When (4), (5), and (6) are combined, u(t) can be expressed as follows:

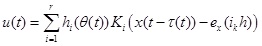(7)

Remark 1: We could see from formula (7) that the control variable contained not only the state variable but also the state error e (ikh) of the event-triggered condition. This makes the computation of the control variable rely on both system state and system error, that is, the introduction of the event-triggered condition.

Supposing fault distribution matrices Ei = - (Bi + ΔBi) and, i = 1,2,...,r, Lu(t) = t (t) - f(t) for the sake of f(t) is actuator fault, where unknown matrix L = diag{l1,...lm}, lq ϵ[0,1], q = 1,2,...,m describes the fault extent of system actuators; that is lq = 0, indicates that the qth actuator is totally invalid; lq = 1 indicates that the actuator operates properly; and lq = ϵ (0,1) indicates that the qth actuator is at fault to some extent.

The fault model of NNCS can be transformed from (2) to (8) and (9):

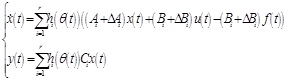(8)
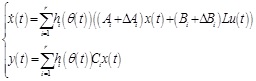(9)

NNCS fault model (8) is equivalent to (9), that is, although they are different in form, they have essentially the same meaning. The model integrates event-triggered condition, network-induced delay, model uncertainties, actuator failures, and control law into a unified framework, which lays a solid foundation for the design of hybrid active–passive fault-tolerant controller for NNCS.

2.4. Related Lemma

Lemma 1 (Schur Complement). For a given symmetric matrix 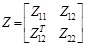, the following three conditions are equivalent:

1) Z < 0;

2) ,

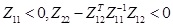3) .

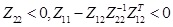Lemma 2. For any positive definite symmetric matrix W ϵ Rn × n, W=WT > 0, scalar, 0 ≤ h(t) ≤ hM and vector function 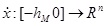, such that the following integration is well defined:

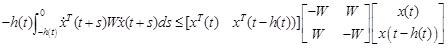Lemma 3 [20P. Park, J.W. Ko, and C. Jeong, "Reciprocally convex approach to stability of systems with time-varying delays", Automatica, vol. 47, no. 1, pp. 235-238, 2011.
[http://dx.doi.org/10.1016/j.automatica.2010.10.014] ]. Let f1, f2,...,fN: Rm → R have positive values in an open subset D of Rm. Then, the reciprocally convex combination of fi over D satisfies

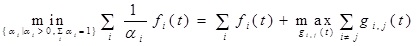Subject to

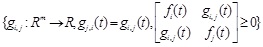Lemma 4 [21L. Xie, "Output feedbackcontrol of systems with parameter uncertainty", International Journal of Control, vol. 63, no. 4, pp. 741-750, 1996.
[http://dx.doi.org/10.1080/00207179608921866] ]. Given matrices Y, M, E with appropriate dimensions and Y = YT, then 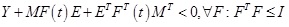holds if and only if, for some scalar ε > 0 and

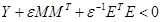
3. RESULTS AND DISCUSSION

3.1. Design of the Fault Detection Observer

Considering system model (2) for NNCS, if there is no actuator failure, the system state is observable. Supposing 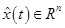represents the estimated state of x(t), then 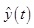is the output of the observer. According to PDC algorithm and formula (8), fault detection observer is designed as follows:

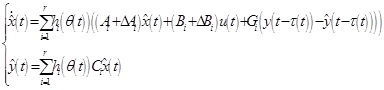(10)

where Gi is the gain matrix of the state observer.

Residual, state estimate error, and residual error are defined as follows, respectively:

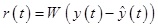(11)
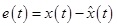(12)
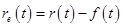(13)

where W is the residual gain matrix and as a result,

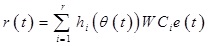(14)
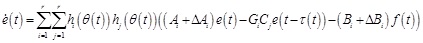(15)
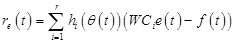(16)

The observer-based fault estimation method is derived from H∞ control theory. In other words, the observer and residual error of real system satisfied such relationship 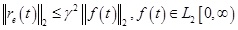, where γ is a given constant.

Define H∞ performance index as .

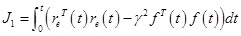Theorem 1. For the given positive scalar τm, τM, τs, a, b, c, ε, if there exists positive definite symmetric matrices, P, Vi, W Qi (i = 1, 2,...,5) which satisfied the following LMI:

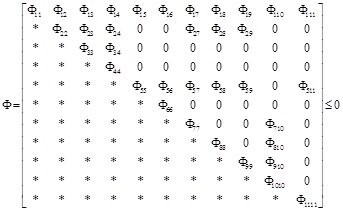where * represents the corresponding matrix to be obtained through the symmetric matrix.

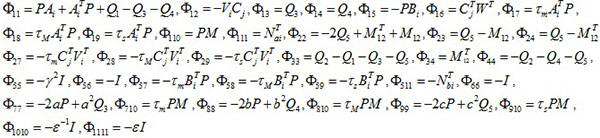We obtain the observer gain matrix through Gi = P-1 Vi and the fault detection observer could ensure the fault estimation error meets the requirement of .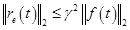

Proof.

Constructing Lyapunov–Krasovskii function is shown as follows:

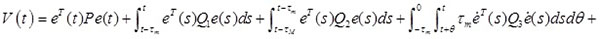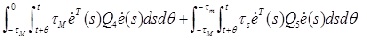For the sake of convenience in writing, we take the following abbreviated forms:

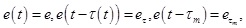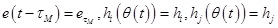
Taking the derivation of V(t) along the trajectory of (15), we obtain

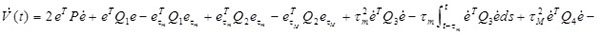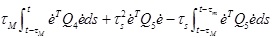(17)

According to lemma 2, we have

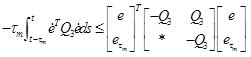(18)
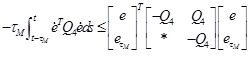(19)

According to lemma 3, we obtain

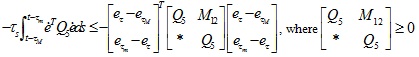(20)
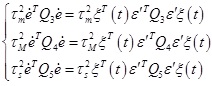(21)

where,

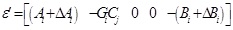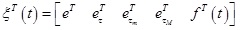
When (17)-(21) are combined, we have

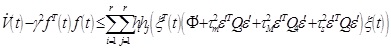
where *represents the corresponding matrix to be obtained through the symmetric matrix.

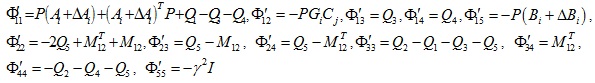From formula (16), we have .

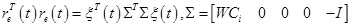Therefore, from the above derivation, we obtain

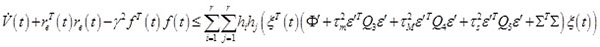Set 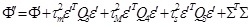, and applying Schur Complement to Φ'', we obtain

where *represents the corresponding matrix to be obtained through the symmetric matrix.

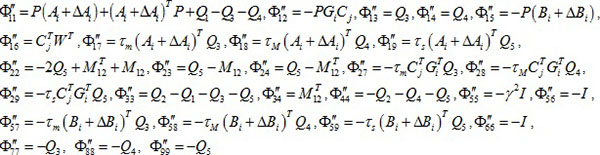According to lemma 4, transforming Φ'' into, 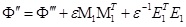where

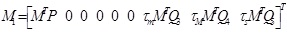
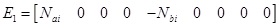
where * represents the corresponding matrix to be obtained through the symmetric matrix.

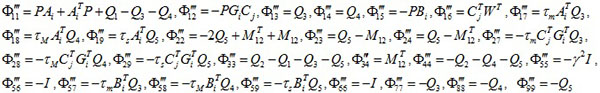Applying Schur Complement to Φ", we obtain

where * represents the corresponding matrix to be obtained through the symmetric matrix.

Before and after multiplying Φ" with diag {I,I,I,I,I,I, PQ3-1, PQ4-1, PQ3-1, I,I}and from the following inequality 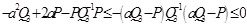, we obtain .

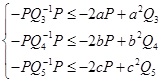Define PGi = Vi, then we obtain Φ.

As previously described, we could make the following conclusions:

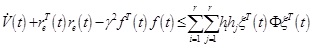When formula f (t) = 0 is true, and LMI Φ < 0, then 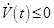could be driven and the error system is asymptotically stable.

For any non-zero, f (t) ϵ [0,∞) the integral previous formula from t 0 → t and we obtain

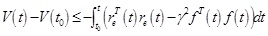Under zero initial condition, when t → ∞, 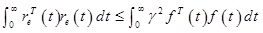, is tenable, that is, 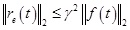. Thus, the error system (16) finally uniformly bounded as well as satisfied the previou H∞ sper formance index; furthermore, the observer gain matrix could be calculated through Gi = P-1Vi.

The proof to theorem 1 is hereby completed.

Remark 2: In this proof, we adopted an improved Jensen inequality technique, which possesses tighter integration upper and lower bounds. For T-S fuzzy system, the application of this method is computationally efficient while possessing less conservativeness compared with liberty matrix method.

3.2. Design of Hybrid Fault-tolerant Controller

3.2.1. Design of AFTC

Assuming rank (F, Ei) = rank = (F) is true first, according to the theorem from literature [22Q. Aibing, J. Honggang, and G. Juping, "Optimal integrated design of time-varying fault estimation and accommodation for non-uniformly sampled data systems", Acta Automatica Sinica, vol. 40, no. 7, pp. 1493-1504, 2014.], under the circumstances of the previous assumptions, there exists a matrix F+ ϵ Rm × n that makes the following equality (1 + FF+) Ei = 0, workable.

The set hybrid fault-tolerant compensation controller based on fault detection observer is

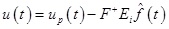(22)

where F+ is the right false inverse matrix of Bi + ΔBi, up(t)is the designed PFTC from theorem 3, and 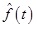represents the estimate value of fault.

For the sake of convenience in writing, we take the following abbreviated forms:

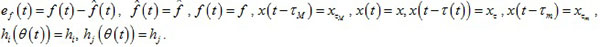Applying (22) to (8), we obtain

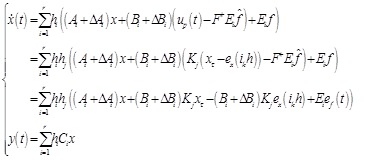(23)

where ef (t) represents fault estimate error.

In consideration of FDO designed in theorem 1, it could ensure that the error system is asymptotically stable, so ef (t) can be seen a kind of external disturbance W (t), and formula (23) can be transformed into (24):

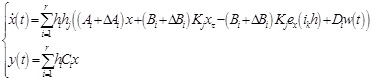(24)

where, Di = Ei = - (Bi + ΔBi), w(t) = ef(t).

Theorem 2. Under the event-triggered condition (3) in the DETCS, for the given constants, 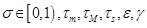the hybrid fault-tolerant controller (22) could keep the system stable and satisfy the following H∞ performance index:

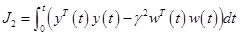(25)

If there exists some positive definite symmetric matrices Ri > 0,i = 1,2,...5 and V, Yj. For any possible actuator failures in mode set L and acceptable parameter uncertainties, these parameters satisfied the following LMI:

where * represents the corresponding matrix to be obtained through the symmetric matrix.

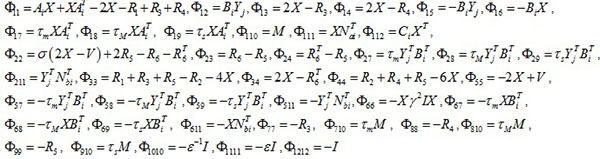
Proof.

Constructing Lyapunov–Krasovskii function as the following:

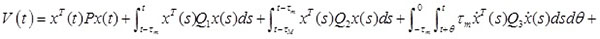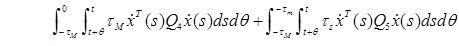where PT = P > 0, QiT = Qi> 0, i = 1,2,3,4,5.

Taking the derivation of V (t)along the trajectory of (24), we obtain

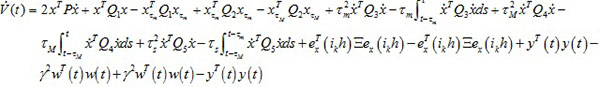For transmission mechanism (3), when ikh ϵ [tkh,tk+1h] , then the following inequality:

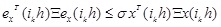is true.

Meanwhile, according to lemma 2, we have

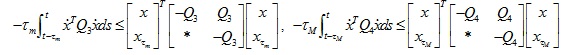According to lemma 3, we obtain

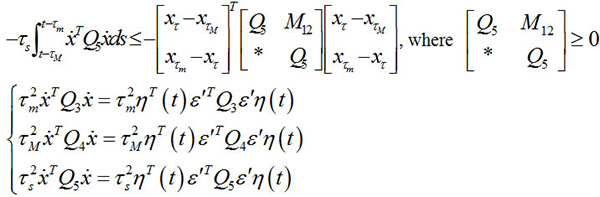where

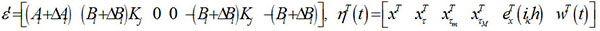
The proof process is same as theorem 1, and then we have:

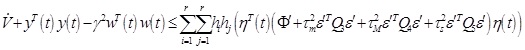where * represents the corresponding matrix to be obtained through the symmetric matrix.

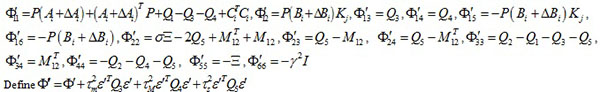Applying Schur Complement to Φ", we have

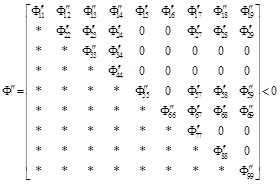where * represents the corresponding matrix to be obtained through the symmetric matrix.

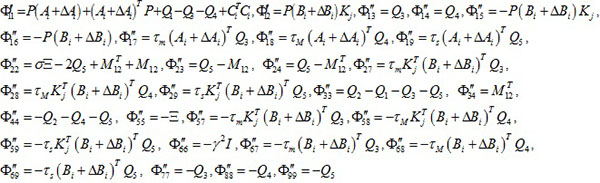
According to lemma 4, transforming Φ" into, 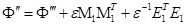where

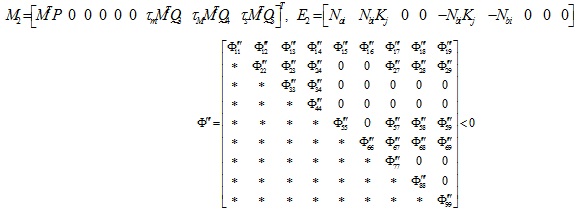
where *represents the corresponding matrix to be obtained through the symmetric matrix.

,

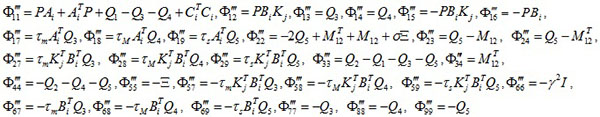Applying Schur Complement to Φ" again, we get

where * represents the corresponding matrix to be obtained through the symmetric matrix.

Before and after multiplying Ф" with

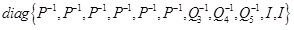
Define 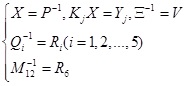and take the following formal transformation:

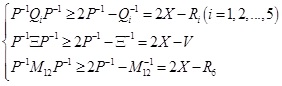
We obtain LMI Φ, where Kj= YjX-1 is the gain matrix to be designed 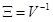, and is the event-triggered weight matrix to be determined.

As previously described, we could make the following conclusions:

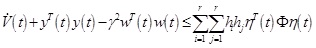, when both w(t) = 0 and LMI Φ < 0 are true, then 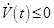could be driven and the error system is asymptotically stable.

For any non-zero w(t) ϵ [0, ∞), integral is the previous formula from t 0 → t and we obtain

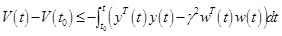
Under zero initial condition, when t → ∞, then 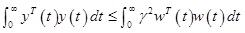is tenable, that is, 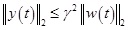. Thus, the fault model (24) has γ rejection performance of disturbance.

The proof to theorem 2 is hereby completed.

3.2.2. Design of PFTC

Aimed at system fault model (9), PFTC is designed as follows:

According to formula (7), the state-feedback controller could be written as 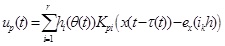where Kpi represents the gain matrix of the PFTC, which ensures that the system is asymptotically stable in the event of any possible actuator failure.

Theorem 3. Under the event-triggered condition (3) in the DETCS, for the given constants 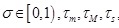, if there exist positive definite symmetric matrices Ri > i = 1,2,...5 X and, V, Yi for any possible actuator failures in mode set L and acceptable parameter uncertainties, these parameters satisfy the following LMI:

where * represents the corresponding matrix to be obtained through the symmetric matrix.

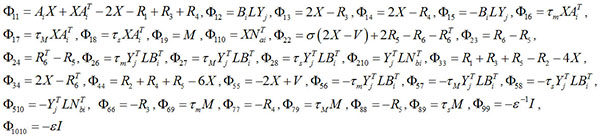then there exists state-feedback control law (7), which keeps the NNCS fault model (9) asymptotically stable, where controller gain matrix and event-triggered weight matrix could be computed through kj = yj X -1 and Ξ = V -1, respectively.

Remark 3. When 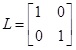, then kj = yj X -1 and Ξ = V -1 are normal controller gain matrix KN and event-triggered weight matrix, ΞN respectively.

4. SIMULATION AND RESULT ANALYSIS

The NNCS model data in literature [18W. Jun, L. Wei, and G. Ling, "Fuzzy observer-based robust guaranteed cost fault-tolerant design for nonlinear NCS", Open Electrical and Electronic Engineering Journal, vol. 8, no. 1, pp. 71-76, 2014.
[http://dx.doi.org/10.2174/1874129001408010071] ] and the fuzzy membership function as M1(x2) = sin2x2 and M2(x2) = cos2x2 are adopted. The system model is expressed as the following T-S fuzzy system of two rules.

R1: If x2 is M1, then

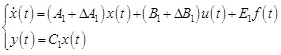
R2: If x2 is, M2 then

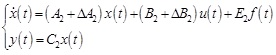
where, .

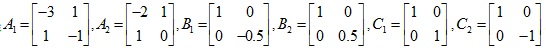Matrices ΔAi, ΔBi(i = 1,2) satisfied the following relationship: [ΔAi ΔBi] MF(t)[NaiNbi] and

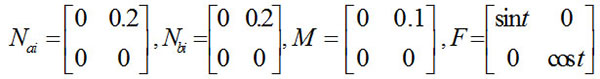We set the parameters as follows: .

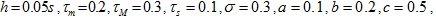
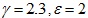Actuator fault matrixis L defined as follows: .

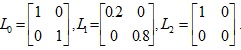where L 0 means that both of the actuators are normally operated, L1 means that both of the actuators are at fault to some extent, and L2 means that one of the actuators is totally faulty and the other one is normally operated.

According to theorem 3, we obtain the state-feedback controller gain matrices and the event-triggered weight matrix as the following:

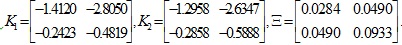Similarly, according to theorem 1, we obtain the FDO gain matrices and the residual gain matrix as follows:

Assuming the system operates normally before t = 5s and known faults begin to appear at the instant t = 5s, unknown fault such as 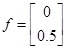begins to appear at time t = 10s.

The simulation results are shown as follows: The response curve of the estimation of faults is shown in Fig. (2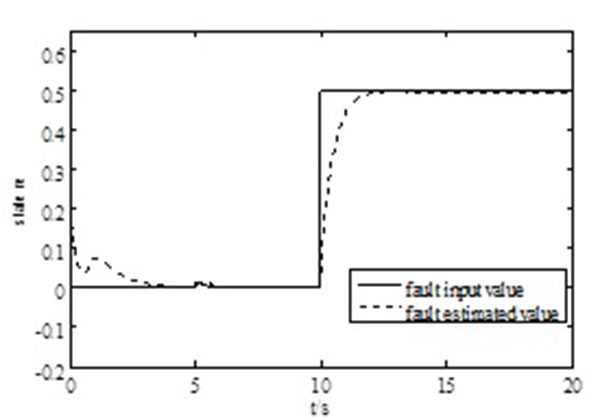). Setting initial condition x(0) = [2-2]T, under the aforementioned actuator failures in mode set L, and the results contrasting figures of state componentin x1, x1 in passive (S1), active (S2), and hybrid (S3) fault-tolerant control are shown in Fig. (3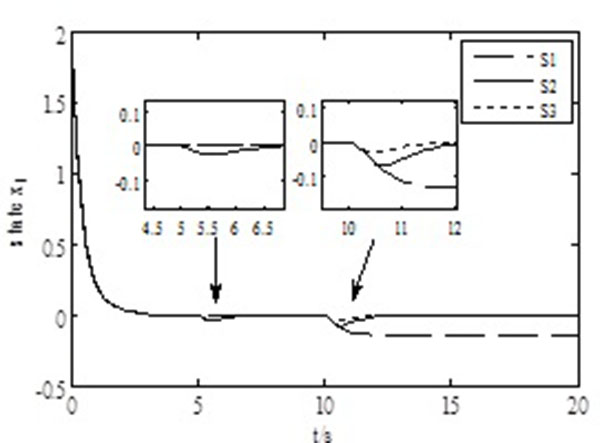) and Fig. (4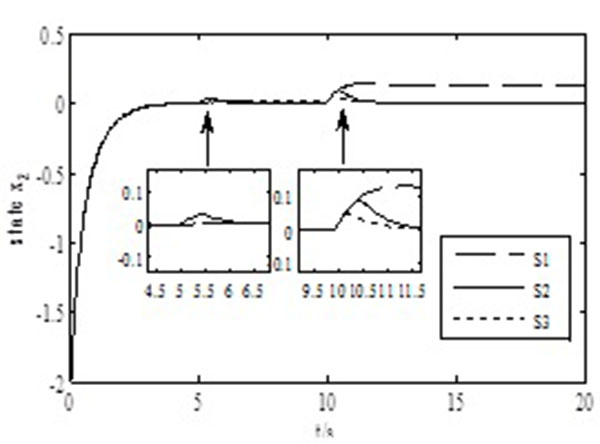), respectively. Similarly, under event-triggered condition (1) in the DETCS and with simulation time, the relationship between release time(s) and release interval of data transmission is shown in Fig. (5).

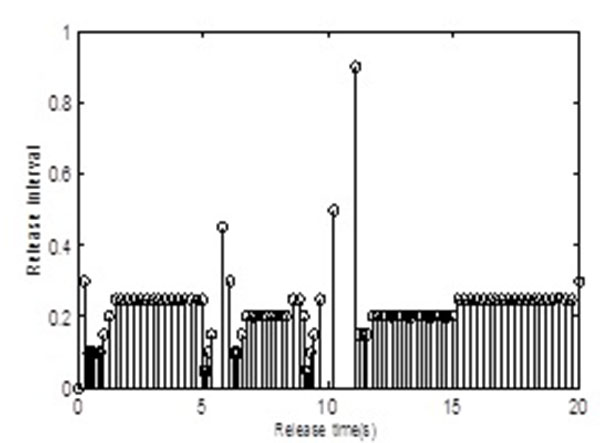Fig. (2)
Response curve of the estimation of faults


Fig. (3)
Response curve of statein different control action.


First, we can draw the conclusion from Fig. (2) that the FDO we designed could estimate the value of any faults timely and accurately compared with fault input value. Although the fault-estimated value lag behind at the instants t = 5s and t = 10s, they fit closely at all other times, which illustrated the validity of the fault estimation method that we have adopted.

Figs. (3) and (4) show that when an actuator operates normally, both AFTC and PFTC could maintain system stability; when an actuator appears at known faults (t = 5s), PFTC could be tolerant on the fault effectively and keeps the system stable. By contrast, AFTC needs time to reconstruct a controller, according to the detected fault information. This requirement wastes time in helping the system recovery become stable. Thus, a short time of oscillation appeared at first, and then the system performance recovered after compensating the impact of fault to the system; on the contrary, when unknown faults happen (t = 10s), PFTC loses the ability to tolerate faults, and the system becomes unstable. Nonetheless, AFTC begins to show its superiority. AFTC has already estimated the value of fault accurately before the system turned into an unstable state and a reconstructed controller according to the estimated fault value. Therefore, the system became stable again. Adopting hybrid fault-tolerant control method not only can keep the system stable when known failure happens but also can slow down the rate of the system performance deterioration when unknown fault occurs. Meanwhile, reconstructing a controller rapidly makes the system recovery stable. Most of all, hybrid active–passive fault-tolerant control method combined the merits of AFTC and PFTC, which contribute much to the improvement of the system’s performance superiority.

To illustrate that the addition of event generator saves network resources to some extent, we adopt a simulation of 20 s whose horizontal axis represents the instants of data transmission tkh and vertical axis represents the release interval between tkh and ikh. Fig. (5) shows that the system sampled 400 times theoretically, but only 128 times transmission practically; the longer the vertical axis value is, the lesser transmission quantity as well as the better quality the system has. Hence, from Fig. (5), we can conclude that the introduction of event-triggered condition reduced network resources and, as a result, increased the efficiency of network utilization.

Fig. (4)
Response curve of statein different control action.


Fig. (5)
Release time(s) and release interval of data transmission for hybrid active–passive fault-tolerant control of NNCS based on DETCS.


CONCLUSION

This paper studied uncertain NNCS with time-varying delay and any actuator failure based on DETCS; under the circumstance of reduced network resources, the integrated-design method of FDO and hybrid active–passive robust fault-tolerant controller is researched. As has been demonstrated in the above chapter, this new method combined the merits of AFTC and PFTC, helped the system in detecting fault information effectively, determined whether the information is time-varying or not, and ensured the stability of the system, whatever type the fault belonged to. Finally, a numerical example is given to show the economy of DETCS to network resources and the effectiveness of the proposed method.

CONFLICT OF INTEREST

The authors confirm that this article content has no conflict of interest.

ACKNOWLEDGEMENTS

In this paper, the research was sponsored by the National Natural Science Foundation of China (Grant No. 61463030).

REFERENCES
[1] L. Huolong, A Study on Design of Passive Fault-tolerant Control System Based on LMI Approach., Northeastern University, 2010.
[2] Q. Shen, B. Jiang, P. Shi, and C.C. Lim, "Novel neural networks-based fault tolerant control scheme with fault alarm", IEEE Transactions on Cybernetics, vol. 44, no. 11, pp. 2190-2201, 2014.
[http://dx.doi.org/10.1109/TCYB.2014.2303131] [PMID: 25014982]
[3] H. Huang, X.D. Han, D.X. Xie, and Z.Q. Wang, "Active fault-tolerant control for networked control systems with packet dropout", Control and Decision, vol. 24, no. 8, pp. 1126-1131, 2009.
[4] H. Songlin, Analysis and Synthesis of Networked Control Systems with Event-Triggering Scheme., Huazhong University of Science & Technology, 2012.
[5] W. Jun, L. Shuzhen, and L. Wei, "Design of hybrid fault-tolerant networked control system based on event-triggered scheme", Journal of Shanghai Institute of Technology, vol. 15, no. 2, pp. 178-184, 2015. [Natural Science].
[6] Y. Wang, Y. Sun, C. Chang, and Y. Hu, Model-Based Fault Detection and Fault Tolerant Control of SCR Urea Injection System., Vehicular Technology, 2015.
[7] M.K. Seyed, S. Karim, and J.Y. Mohamad, "Multiple model-based fault detection and diagnosis for nonlinear model predictive fault-tolerant control", Arabian Journal for Science and Engineering, vol. 39, no. 10, pp. 7433-7442, 2014.
[http://dx.doi.org/10.1007/s13369-014-1252-y]
[8] H.R. Karimi, M. Chadli, S. Peng, and Z. Lixian, "Fault detection, isolation, and tolerant control of vehicles using soft computing methods", IET Control Theory & Applications, vol. 8, no. 9, pp. 655-657, 2014.
[http://dx.doi.org/10.1049/iet-cta.2014.0577]
[9] M. Mongi, B.A. Hechmi, F. Khaled, J. Mohamed, and B. Mohamed, "Fault detection and fault-tolerant control of power converter fed PMSM", Electrical Engineering, vol. 98, no. 2, pp. 121-131, 2016.
[http://dx.doi.org/10.1007/s00202-015-0350-5]
[10] M.M. Seron, J.A. De Dona, and J.H. Richter, "Integrated sensor and actuator fault-tolerant control", International Journal of Control, vol. 86, no. 4, pp. 689-708, 2013.
[http://dx.doi.org/10.1080/00207179.2012.757653]
[11] Hy. Cho, S.M. Fei, D. Yue, C. Peng, and J.T. Sun, "Quantized control for nonlinear networked control systems", Fuzzy Sets and Systems, vol. 1174, pp. 99-113, 2011.
[http://dx.doi.org/10.1016/j.fss.2011.01.011]
[12] T. Steffen, F. Schiller, M. Blum, and R. Dixon, "Analysing the reliability of actuation elements in series and parallel configurations for high-redundancy actuation", International Journal of Systems Science, vol. 44, no. 8, pp. 1504-1521, 2013.
[http://dx.doi.org/10.1080/00207721.2012.659694]
[13] M. Takahashi, and T. Takagi, "Adaptive fault-tolerant control based on hybrid redundancy", Asia-Pacific Journal of Chemical Engineering, vol. 7, no. 5, pp. 642-650, 2012.
[http://dx.doi.org/10.1002/apj.1628]
[14] L. Jinliang, Z. Gu, and F. Shumin, "Reliable control for nonlinear systems with stochastic actuators fault and random delays through a T-S fuzzy model approach", Acta Mathematicae Applicatae Sinica, vol. 32, no. 2, pp. 395-406, 2016.
[http://dx.doi.org/10.1007/s10255-016-0566-9]
[15] X Zhao, and Y Yin, "Control of switched nonlinear systems via T-S fuzzy modeling", IEEE Transactions on Fuzzy Systems, 2015.
[16] T. Zhou, and H. Xiqin, "An improved H∞ filter design for nonlinear systems described by T-S fuzzy models with time-varying delay", International Journal of Automation and Computing, vol. 12, no. 6, pp. 671-678, 2015.
[http://dx.doi.org/10.1007/s11633-015-0930-x]
[17] H. Li, L. Wu, J. Li, F. Sun, and Y. Xia, "Stabilization and Separation Principle of Networked Control Systems Using the T–S Fuzzy Model Approach", IEEE Transactions on Fuzzy Systems, vol. 23, no. 5, pp. 1832-1843, 2015.
[http://dx.doi.org/10.1109/TFUZZ.2014.2382131]
[18] W. Jun, L. Wei, and G. Ling, "Fuzzy observer-based robust guaranteed cost fault-tolerant design for nonlinear NCS", Open Electrical and Electronic Engineering Journal, vol. 8, no. 1, pp. 71-76, 2014.
[http://dx.doi.org/10.2174/1874129001408010071]
[19] L. Wei, and Y. Kun, "Integrity design of uncertainty nonlinear networked control system based on discrete event-triggered scheme", Journal of Lanzhou University of Technology, vol. 41, no. 2, pp. 83-90, 2015.
[20] P. Park, J.W. Ko, and C. Jeong, "Reciprocally convex approach to stability of systems with time-varying delays", Automatica, vol. 47, no. 1, pp. 235-238, 2011.
[http://dx.doi.org/10.1016/j.automatica.2010.10.014]
[21] L. Xie, "Output feedbackcontrol of systems with parameter uncertainty", International Journal of Control, vol. 63, no. 4, pp. 741-750, 1996.
[http://dx.doi.org/10.1080/00207179608921866]
[22] Q. Aibing, J. Honggang, and G. Juping, "Optimal integrated design of time-varying fault estimation and accommodation for non-uniformly sampled data systems", Acta Automatica Sinica, vol. 40, no. 7, pp. 1493-1504, 2014.
Track Your Manuscript:


Endorsements



"Open access will revolutionize 21st century knowledge work and accelerate the diffusion of ideas and evidence that support just in time learning and the evolution of thinking in a number of disciplines."


Daniel Pesut
(Indiana University School of Nursing, USA)

"It is important that students and researchers from all over the world can have easy access to relevant, high-standard and timely scientific information. This is exactly what Open Access Journals provide and this is the reason why I support this endeavor."


Jacques Descotes
(Centre Antipoison-Centre de Pharmacovigilance, France)

"Publishing research articles is the key for future scientific progress. Open Access publishing is therefore of utmost importance for wider dissemination of information, and will help serving the best interest of the scientific community."


Patrice Talaga
(UCB S.A., Belgium)

"Open access journals are a novel concept in the medical literature. They offer accessible information to a wide variety of individuals, including physicians, medical students, clinical investigators, and the general public. They are an outstanding source of medical and scientific information."


Jeffrey M. Weinberg
(St. Luke's-Roosevelt Hospital Center, USA)

"Open access journals are extremely useful for graduate students, investigators and all other interested persons to read important scientific articles and subscribe scientific journals. Indeed, the research articles span a wide range of area and of high quality. This is specially a must for researchers belonging to institutions with limited library facility and funding to subscribe scientific journals."


Debomoy K. Lahiri
(Indiana University School of Medicine, USA)

"Open access journals represent a major break-through in publishing. They provide easy access to the latest research on a wide variety of issues. Relevant and timely articles are made available in a fraction of the time taken by more conventional publishers. Articles are of uniformly high quality and written by the world's leading authorities."


Robert Looney
(Naval Postgraduate School, USA)

"Open access journals have transformed the way scientific data is published and disseminated: particularly, whilst ensuring a high quality standard and transparency in the editorial process, they have increased the access to the scientific literature by those researchers that have limited library support or that are working on small budgets."


Richard Reithinger
(Westat, USA)

"Not only do open access journals greatly improve the access to high quality information for scientists in the developing world, it also provides extra exposure for our papers."


J. Ferwerda
(University of Oxford, UK)

"Open Access 'Chemistry' Journals allow the dissemination of knowledge at your finger tips without paying for the scientific content."


Sean L. Kitson
(Almac Sciences, Northern Ireland)

"In principle, all scientific journals should have open access, as should be science itself. Open access journals are very helpful for students, researchers and the general public including people from institutions which do not have library or cannot afford to subscribe scientific journals. The articles are high standard and cover a wide area."


Hubert Wolterbeek
(Delft University of Technology, The Netherlands)

"The widest possible diffusion of information is critical for the advancement of science. In this perspective, open access journals are instrumental in fostering researches and achievements."


Alessandro Laviano
(Sapienza - University of Rome, Italy)

"Open access journals are very useful for all scientists as they can have quick information in the different fields of science."


Philippe Hernigou
(Paris University, France)

"There are many scientists who can not afford the rather expensive subscriptions to scientific journals. Open access journals offer a good alternative for free access to good quality scientific information."


Fidel Toldrá
(Instituto de Agroquimica y Tecnologia de Alimentos, Spain)

"Open access journals have become a fundamental tool for students, researchers, patients and the general public. Many people from institutions which do not have library or cannot afford to subscribe scientific journals benefit of them on a daily basis. The articles are among the best and cover most scientific areas."


M. Bendandi
(University Clinic of Navarre, Spain)

"These journals provide researchers with a platform for rapid, open access scientific communication. The articles are of high quality and broad scope."


Peter Chiba
(University of Vienna, Austria)

"Open access journals are probably one of the most important contributions to promote and diffuse science worldwide."


Jaime Sampaio
(University of Trás-os-Montes e Alto Douro, Portugal)

"Open access journals make up a new and rather revolutionary way to scientific publication. This option opens several quite interesting possibilities to disseminate openly and freely new knowledge and even to facilitate interpersonal communication among scientists."


Eduardo A. Castro
(INIFTA, Argentina)

"Open access journals are freely available online throughout the world, for you to read, download, copy, distribute, and use. The articles published in the open access journals are high quality and cover a wide range of fields."


Kenji Hashimoto
(Chiba University, Japan)

"Open Access journals offer an innovative and efficient way of publication for academics and professionals in a wide range of disciplines. The papers published are of high quality after rigorous peer review and they are Indexed in: major international databases. I read Open Access journals to keep abreast of the recent development in my field of study."


Daniel Shek
(Chinese University of Hong Kong, Hong Kong)

"It is a modern trend for publishers to establish open access journals. Researchers, faculty members, and students will be greatly benefited by the new journals of Bentham Science Publishers Ltd. in this category."


Jih Ru Hwu
(National Central University, Taiwan)

Browse Contents




Webmaster Contact: info@benthamopen.net
Copyright © 2023 Bentham Open