- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Fuels & Energy Science Journal
(Discontinued)
ISSN: 1876-973X ― Volume 11, 2018
Chemical Tank Leakage Risk Assessment Based on Set Pair Analysis and LabVIEW
Yiyuan Cui*, Bing Wu
Abstract
Chemical storage tank leakage in petrochemical wharf is a serious economic, environmental and safety problem. Risk assessment is an effective way to identify chemical storage tank hazards and provides a guide for accident prevention in petrochemical wharf enterprises. Based on the characteristics of chemical storage tank zone, this paper proposes a real-time relative risk assessment method. Firstly, the disastrous consequences of chemical storage tank leakage are analyzed and quantified. Then, the set-pair analysis is employed to construct a relative risk assessment model. Finally, a computer program is developed to simulate chemical storage tank leakage and achieve a real-time risk assessment. A case study is conducted to verify the effectiveness of this method. The results show that the relative risks of different chemical storage tanks will change with the variation of storage quantity. The proposed method and developed program are valid for assessing risks of chemical storage tank leakage in petrochemical wharf, and may be helpful to manage chemical storage tank hazards of petrochemical wharf enterprises and to provide corresponding safety precaution as well.
Article Information
Identifiers and Pagination:
Year: 2016Volume: 9
First Page: 102
Last Page: 113
Publisher Id: TOEFJ-9-102
DOI: 10.2174/1876973X01609010102
Article History:
Received Date: 03/08/2016Revision Received Date: 08/11/2016
Acceptance Date: 08/11/2016
Electronic publication date: 07/12/2016
Collection year: 2016
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
* Address correspondence to this author at College of Resource and Safety Engineering, China University of Mining and Technology Beijing, Beijing, China; Tel/Fax: +8618813150978; E-mail: tsuiyiy@163.com.
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 03-08-2016 |
Original Manuscript | Chemical Tank Leakage Risk Assessment Based on Set Pair Analysis and LabVIEW | |
1. INTRODUCTION
Petrochemical wharf enterprises store and transport large volumes of flammable, explosive and toxic materials. As one of the major hazard installations, chemical storage tank is a matter of major concern of safety management in petrochemical industries [1Zhang, X. M.; Chen, C. Mechanism analysis and risk assessment of escalation scenario in chemical industry zones. Process Saf. Environ. Prot., 2013, 91(s 1-2), 79-85.
[http://dx.doi.org/10.1016/j.psep.2012.02.003] ]. According to the statistical analysis of a large number of accidents, fire, explosion and poisoning caused by chemical storage tank leakage were considered the most common accidents in petrochemical enterprises [2Chang, J.I.; Lin, C.C. A study of storage tank accidents. J. Loss Prev. Process Ind., 2006, 19(1), 51-59.
[http://dx.doi.org/10.1016/j.jlp.2005.05.015] ]. Therefore, the risk assessment of chemical tank leakage is very important to prevent accidents and to guarantee the healthy development of petrochemical wharf enterprises.
For a long time, scholars have employed methods such as Dow F&E index [3Leur, P.D.; Sayed, T. Development of a road safety risk index. Transp. Res. Rec., 2002, 1784(1), 33-42.
[http://dx.doi.org/10.3141/1784-05] ], relative risk index, ICI/MOND [4Misra, K.B.; Weber, G.G. A new method for fuzzy fault tree analysis. Microelectron. Reliab., 1989, 29(2), 195-216.
[http://dx.doi.org/10.1016/0026-2714(89)90568-4] ], and Fault Tree Analysis [5Rahman, M.; Heikkilä, A.M.; Hurme, M. Comparison of inherent safety indices in process concept evaluation. J. Loss Prev. Process Ind., 2005, 18(4), 327-334.
[http://dx.doi.org/10.1016/j.jlp.2005.06.015] ] to assess the industrial hazard installations. But these methods are only applied to evaluate single installation and obtain its absolute risk. As a temporary storage place and an important part of petrochemical wharf enterprises, chemical storage tank zone usually contains different chemicals with real-time storage variation. Compared with absolute risk, the relative risks [6Zhong, M.D. China Safety Science Journal, 1997, 7(2), 6-9.] of different chemical storage tanks are more helpful to identify the key objectives of safety management in petrochemical wharf enterprises. Moreover, these methods require long term of data collection, which cannot achieve real-time risk assessing. To evaluate multi chemical hazards precisely and obtain real-time results, it is essential to propose a real-time relative risk assessment method.
The objective of this study is to (a) adequately analyze the characteristics of chemical storage tank leakage, (b) construct an effective risk assessment model, (c) use computer to achieve rapid evaluation. Therefore, this study firstly analyzes and quantifies the derivative accidents of chemical storage tank leakage, and then integrates the set-pair analysis to establish a relative risk assessment model. Finally, a program is developed to simulate chemical storage tank leakage and achieve real-time risk assessing. It is expected that the proposed method and developed program can be effectively used for accident prevention in petrochemical wharf enterprises.
2. METHODOLOGY
2.1. Consequences of Chemical Tank Leakage
There are some potential accidents relating to chemical tank leakage. Generally, the chemicals stored in tanks are flammable, explosive and toxic. After leakage, three types of derivative accidents may be caused, which are pool fire, vapor cloud explosion(VCE) and poisoning [7Si, H.; Ji, H.; Zeng, X. Quantitative risk assessment model of hazardous chemicals leakage and application. Saf. Sci., 2012, 50(7), 1452-1461.
[http://dx.doi.org/10.1016/j.ssci.2012.01.011] ]. In practice, which type of accident occurs is determined by ignition time and probability. Therefore, the process of chemical storage tank leakage can be summarized as:
- The chemical storage tank cracks, liquid chemical flows to the ground and forms a large area of liquid pool.
- The liquid pool is ignited immediately to cause pool fire.
- The liquid pool evaporates, and the generated explosive gas is ignited to cause VCE.
- The explosive gas is not ignited but diffuses to downstream and causes poisoning accidents.
The probability and loss of derivative accidents can be quantified by appropriate model and damage criteria. The risk assessment model can be constructed as follows (Fig. 1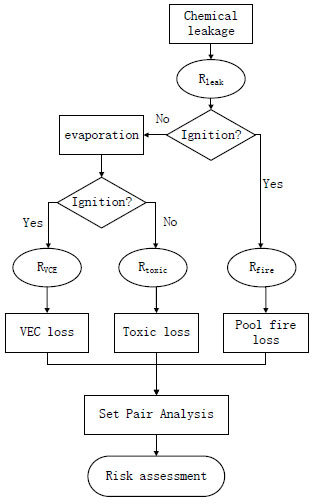 ):
):
 |
Fig. (1) Risk assessment model of chemical storage tank leakage. |
2.2. Probability Calculation
According to previous researches [8Davies, T.; Harding, A.B.; Mckay, I.P.; Robinson, R.G.; Wilkinson, A. Bund effectiveness in preventing escalation of tank farm fires. Process Saf. Environ. Prot., 1996, 74(2), 88-93., 9Spouge, J. New generic leak frequencies for process equipment. Process Saf. Prog., 2005, 24(4), 249-257.
[http://dx.doi.org/10.1002/prs.10100] ], the probability of storage tank leakage is related to crack aperture. In the study of Yu [10Yu, L.J.; Duo, Y.Q.; Shi, L.C.; Wei, L.J.; Wu, Z.Z. Method for determinating probabilities of leaks in quantitative risk assessment. J. Saf. Sci. Technol., 2007, 3(6), 27-30.], a calculation method of random aperture leakage probability was proposed based on statistical data of the probability of different leakage apertures published by Dutch research group(COVO) [11Rijnmond, O. L. Risk analysis of six potentially hazardous industrial objects in the Rijnmond area, a pilot study: a report to the Rijnmond Public Authority; Springer Netherlands, 1982.
[http://dx.doi.org/10.1007/978-94-017-2907-9] ] and DNV [12John, S. New generic leak frequencies for process equipment Process Saf. Prog., 2005, 24(4), 249-257.]. The leakage probability of different crack apertures is presented as follows:
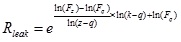 |
(1) |
where Rleak is the leakage probability of crack aperture k, q is the minimum value of the interval containing k, z is the maximum value of the interval containing k, Fz is the leakage probability of crack aperture z, Fq is the leakage probability of crack aperture q. The q, z and their corresponding leakage probabilities are shown in Table 1.
Ignition time determines which kind of disastrous consequences occurs. Immediate ignition will cause pool fire, while retarded ignition will cause vapor cloud explosion and no ignition will cause toxic gas diffusion. Therefore, the probabilities of the three derivative accidents can be denoted by the ignition probability.
In the study of Bai [14Bai, Y.Z.; Engineer, S.; Wen-Yi, E.D.; Zhi-Feng, E.; Xiang-Di, E.Z. Engineer, Determination of ignition source and ignition probability of leaking accidents in petrochemical processes. China Saf. Sci. J., 2010, 20(1), 61-66.], the ignition probability is related to leakage rate. If tank leakage occurs, the leakage rate can be calculated by:
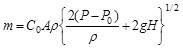 |
(2) |
where m is the mass leakage rate, kg/s, C0 is the leakage coefficient, A is the crack area, m2, P is the internal pressure of tank, Pa, P0 is the external pressure of tank, Pa, H is the height of liquid in storage tank, m.
The total ignition probability can be calculated by
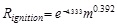 |
(3) |
The probabilities of VCE, pool fire and toxic gas diffusion can be respectively written as:
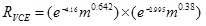 |
(4) |
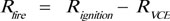 |
(5) |
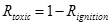 |
(6) |
2.3. Quantification of Disastrous Consequences
For different disastrous consequences, the calculation models and criteria of injury or loss are also different. Thermal strength criteria can be used to quantify fire disasters [15Raj, P. A physical model and improved experimental data correlation for wind induced flame drag in pool fires. Fire Technol., 2010, 46(46), 579-609.
[http://dx.doi.org/10.1007/s10694-009-0107-7] ]. The thermal radiation strength at a certain distance can be obtained by:
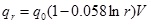 |
(7) |
where qr is the thermal radiation flux received by target, kW/m2, q0 is the thermal flux of fire source, kW/m2, r is the distance between target and fire center, m, V is the view factor.
The injury scope of pool fire can be divided into three zones. If q>37.5 kW/m2, people in this scope will be immediately dead. This scope can be defined as death distance, If 25 kW/m2<q<37.5 kW/m2, people in this scope will suffer second-degree burn. This scope can be defined as the serious injury distance. If 12.5 kW/m2<q<25 kW/m2, people in this scope will suffer first-degree burn. This scope can be defined as the minor injury distance.
Over-pressure is the criterion of evaluating explosion loss. The injury scope of over-pressure can also be divided into three zones [16Tauseef, S.; Abbasi, T.; Abbasi, S. Risks of Fire and Explosion Associated With the Increasing Use of Liquefied Petroleum Gas. J. Fail. Anal. Prev., 2010, 10(4), 322-333.
[http://dx.doi.org/10.1007/s11668-010-9360-9] ]. The first zone is the death zone, which can be obtained by Eqs.(8-10):
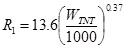 |
(8) |
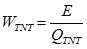 |
(9) |
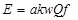 |
(10) |
where R1 is the radius of death zone, m, WTNT is TNT equivalent, (kg,TNT), E is the total vapor cloud explosion energy, J, QTNT is TNT explosion heat, MJ/kg, a is the combustible gas vapor cloud equivalent coefficient, k is the ground explosion coefficient, Qf is the combustion heat of gas, MJ/kg.
The second and third zones are serious injury and minor injury zones, respectively. The peak over-pressures of these two zones are 44000 Pa and 17000 Pa, respectively. The radius of serious injury and minor injury can be obtained by Eqs (11-13):
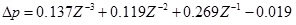 |
(11) |
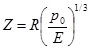 |
(12) |
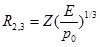 |
(13) |
where ΔP is the maximum shock wave over-pressure, Pa, P0 is the environmental pressure, Pa.
The damage of poisoning has little effect on equipment, but huge impact on human and environment. Generally, the possibility and affecting scope of poisoning are the largest of these three derivative accidents. The calculation of toxic area is related to many factors, such as wind speed, releasing time, and solar radiation. This paper adopts Gaussian model [17Zhang, Q.L.; Dai, Y.R.; Wang, J.; Zhao, R.Y. Research of Toxic Gas Diffusion Simulation Technology Based on Arc Engine; Springer Berlin Heidelberg, 2013, pp. 35-41.
[http://dx.doi.org/10.1007/978-3-642-35470-0_5] ] to describe the process of toxic gas diffusion. The poisoning zones can be divided into dead area, serious injured area and minor injured area. The lowest toxic load concentrations of the three zones are obtained from the IDLH, PC-STEL and Chinese national hygienic standard value of chemicals [18Zhang, H.F. Emergency response poket manual for highly hazardous chemicals; China Petrochemical Press, 2006. ], respectively.
2.4. The Weights of Indexes
In this paper, AHP was adopted to determine the weight of each index. Based on the previous analysis, these 3 derivative accidents and 9 loss indexes compose a 3-layer hierarchic model shown in Fig. (2).
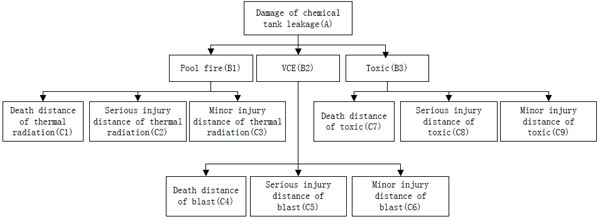 |
Fig.(2) AHP analysis of damage caused by chemical tank leakage. |
The AHP system of chemical storage tank leakage is composed of three layers: goal layer(Ai), criterion layer(Bi) and index layer(Ci). The importance of each factor in same layer can be judged by pair-wise comparison Table 2. Then the judgment matrix Bi,j can be determined based on the experts grading.
The judgment matrix should pass the consistency validation. Therefore, the pair-wise matrix should be checked by:
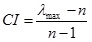 |
(14) |
where CI is the consistency index. The RI is the random consistency index. If the ratio of CI and RI is less than 0.1, the pair-wise comparison matrix will pass the consistency validation and the values of weighting are acceptable.
The judgment matrix of criterion layer(Bi) is shown in Table 3
The weights of wi can be obtained by;
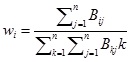 |
(15) |
Finally, the weight set of the criterion layer to goal layer is:
B = (0.2599, 0.3275, 0.4126)The weight of index layer(Ci) to criterion layer can also be calculated by the same method, which is shown as:
C1= (0.6531, 0.2323,0.1146)C2= (0.6157, 0.2474, 0.1369)C3= (0.122, 0.5584, 0.3196)2.5. Set Pair Analysis
The set pair analysis(SPA) is a systemic method to deal with fuzzy problems. The main idea of this method is that the fuzzy problem is an integrated certain-uncertain system, which is composed of certain factors and uncertain factors. The certain factors can be defined as identity factors or contrary factors and the uncertain factors can be defined as discrepancy factors. SPA sets up a connection function to describe a couple of sets’ identity degree, discrepancy degree and contrary degree. The connection coefficient can be used to describe the relationship of two different sets. The connection function of set-pair is as below:
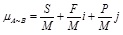 |
(16) |
where uA~B is the connection degree of two sets, M is the total number of feature. S is the the number of identity characteristics, F denotes the number of uncertain characteristics, P represents the number of contrary characteristics. The j is the coefficient of the contrary degree, and is specified as -1. The i is the coefficient of the discrepancy degree, and is an uncertain value between -1 and 1.
2.6. SPA for Chemical Tank Leakage Risk Assessment
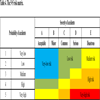
Risk is the combination of severity and possibility. Generally, the risk rank of hazard installation is determined by risk matrix. Table 4 is a 5×5 risk matrix [19Kang, J.; Liang, W.; Zhang, L.; Lu, Z.; Liu, D.; Yin, W.; Zhang, G. A new risk evaluation method for oil storage tank zones based on the theory of two types of hazards. J. Loss Prev. Process Ind., 2014, 29(1), 267-276.
[http://dx.doi.org/10.1016/j.jlp.2014.03.007] ]. Based on this risk matrix, the severity and possibility of derivative accidents can be divided into 5 grades and finally using 5 ranks to describe the relative risks of chemical storage tanks, which are very-low risk, low risk, medium risk, high risk and very-high risk. Therefore, the aim of SPA risk assessment model is to construct a 5-grade severity set-pair and a 5-grade probability set-pair, then determine the location of objective in the risk matrix to obtain the final risk rank. This paper mainly introduces the establishment process of 5-grade severity set-pair, the same way can also be applied to construct the 5-grade probability set-pair.
Since the assessment method proposed in this paper is to obtain the relative risks of multi chemical storage tanks, the standard of each severity grade should be determined by real-time index values of all objectives. Assuming the assessment objectives are p chemical storage tanks and the values of m indexes are v1, v2...,vm, the index matrix is denoted as:
 |
(17) |
The highest and lowest values of each index can establish the upper and lower limit sets respectively, which can be denoted as U={u1,u2,…,um} and D={d1,d2,…,dm}. The interval of two adjacent grades can be expressed as Intk=(uk-dk)/n. In this paper, n equals to 5, which means Intk=(uk-dk)/5.
If the objectives are required to divided into n grades(G1,G2,...,Gn), The connection degree matrix can be denoted as follows:
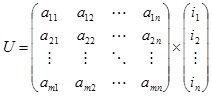 |
(18) |
where ak,j (k=1,...,m, j=1,...,n) stands for the membership between indexes and risk ranks, ij(j=1,...,n) stands for the coefficients of grade Gn..
Based on the principal of SPA, the memership ak,j is a value in the interval of [-1,1]. If the index value vk(k=1,...,m) is in the interval of grade Gj, this index can be defined as identical with this grade and its membership ak,j is a fix number 1. And for adjacent grades, this index can be defined as discrepant with them and its membership ak,j is between -1 and 1. For the rest of the grades, the index is contrary to them, its membership ak,j is -1. ak,j can be determined by:
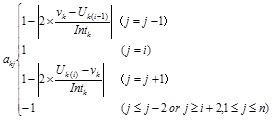 |
(19) |
where Uk(i) is the upper limit of Gi of the index k.
If the weights of indexes are considered, the connection degree can be written as:
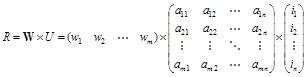 |
(20) |
It can also be represented as:
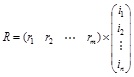 |
(21) |
where 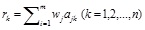 .
.
The final severity grades can be determined by maximum membership degree. If max(r1, r2,....,rn)=rk, the severity grade of chemical storage tank leakage is Gk..
3. DESIGN OF SOFTWARE
The main ideas of program development are: (1) simulate real-time chemical storage tank leakage, (2) quantify the accident severity and probability, (3) construct SPA risk assessment model to evaluate chemical storage tanks. Fig. (3) shows the structure of program. In this program, data input interface, Index & probability calculation module, risk assessment module and result display block are the core parts.
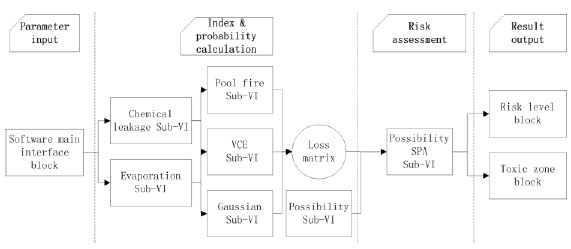 |
Fig. (3) Structure of software in designed system. |
The parameters of chemical storage tank leakage simulation include month, period of the month, day-night, cloud cover, underlying surface, crack shape, crack aperture, geographic coordinates, temperature, time of the accident, wind speed, the evaporation and leakage time and so on. These parameters are all related to the quantification of accident probability and severity. The design of parameter input module is demonstrated in Fig. (4).
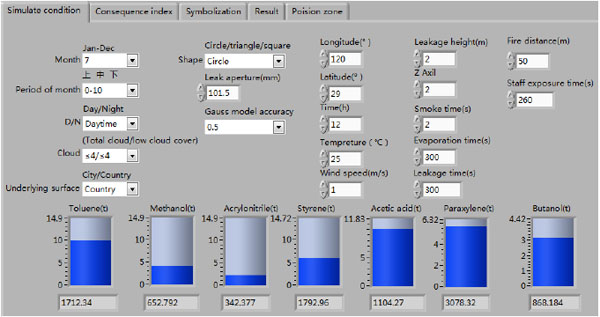 |
Fig. (4) Design of data input module. |
The design of Index & possibility module is shown in Fig. (5). This module firstly simulates the process of chemical storage tank leakage, including the formation of liquid pool, liquid evaporation and toxic gas diffusion, then calculates the derivative accidents’ probabilities and values of loss indexes.
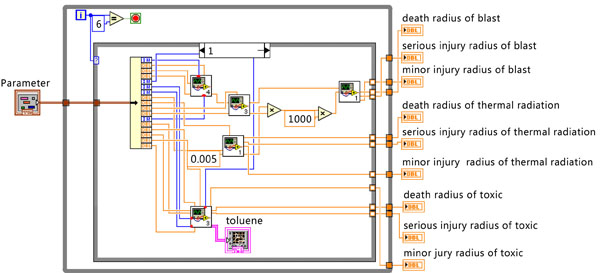 |
Fig. (5) Design of parameter calculation module. |
Set pair algorithm is the core of risk assessment module. The severity grade and probability grade of derivative accidents are determined by set pair algorithm, then the locations of objectives in the 5×5 risk matrix are obtained. Finally, the risk ranks of objectives are outputted in the result show module. The result show module also includes the poisoning zone show block which can directly show the accident influence area. The design of set pair algorithm is shown in Fig. (6) and the demonstration of poisoning zone is shown in Fig. (7).
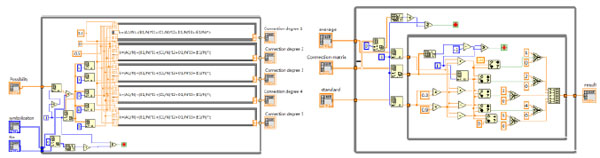 |
Fig. (6) Design of risk assessment module and result output module. |
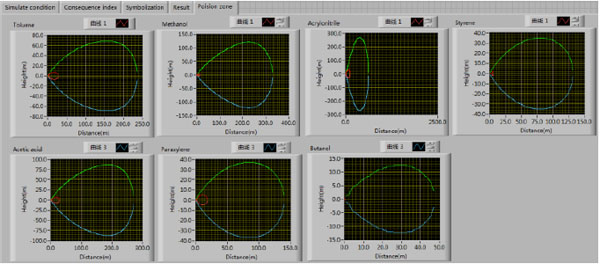 |
Fig. (7) Demonstration of poison zone. |
4. CASE STUDY
Based on the proposed assessment model, the relative risks of 7 chemical storage tanks were evaluated at Qingzhi petrochemical wharf in Ningbo, China. The liquid chemicals stored in these storage tanks are toluene, methanol, acrylonitrile, styrene, acetic acid, paraxylene and butanol, respectively. In reference of the real-time data, leakage accidents of 3 scenarios were simulated.
4.1. Parameter Setting
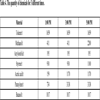
Based on the record of local meteorological conditions and geography feature, the weather conditions of accident simulation were: middle of July, daylight, wind speed 1m/s, 25°C, sunny. Assuming the source of leakage is at the bottom of storage tank, and the crack shape is circular with the diameter of 100 mm. The simulation time is set to 300sec. The real-time data of storage quantity of each storage tank is represented in Table 5.
4.2. Results Analysis
As can be seen from the results of simulation shown in Fig. (8), the risks of chemical storage tanks change when their storage quantities change. This is because different leakage quantities result in differences in the severity and possibility of accidents. Meanwhile, the following phenomena also show the characteristics of the proposed risk assessment method.
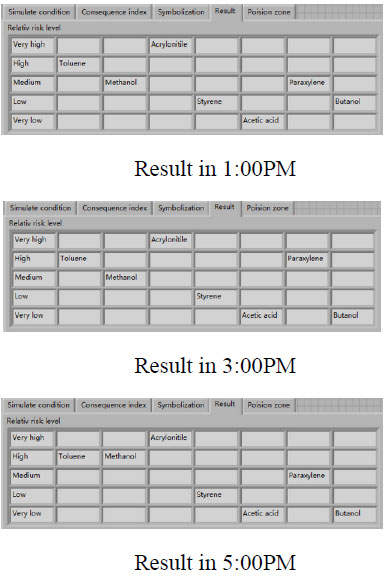 |
Fig. (8) The output of simulation. |
Firstly, although the storage quantity is relative small, acrylonitrile storage tank always possesses the highest risk level. This is because the inherent toxicity of acrylonitrile is very high and poisoning is the most possible derivative accident of chemical tank leakage. Although the storage quantity has always been maintained to 195t, acrylonitrile storage tank is still the hazard source at most risk. Secondly, it also can be seen that the quantity of butanol does not change in 3:00 PM, but its relative risk decreases. This is because the sharp increase of acetic acid and paraxylene changes the interval(Intj)of two adjacent risk rank, the connection degree between butanol and its original risk rank decreases, so butanol falls into the scope of ‘very low risk’. Thirdly, although the storage quantity of acetic acid rose sharply in 3:00 PM, the risk rank of acetic acid chemical storage tank is still the lowest. This is because acetic acid is low toxic and nonflammable, even if the acetic acid storage tank leakage, the severity of its derivative accidents is much smaller than that of other chemical storage tanks leakage. Therefore, it can be seen that the real-time relative risk assessment is reasonable, which can effectively determine the highest risk chemical storage tank and provide references to safety management for petrochemical wharf enterprises.
DISCUSSION AND CONCLUSION
Chemical storage tank leakage is a kind of serious accident in petrochemical wharf enterprises. It is essential to evaluate the risk of chemical storage tanks to determine the key objective of safety management. Since the chemical stored in every storage tank is different and the quantity is quite large, the conventional risk assessment methods cannot effectively differentiate the risks of multi chemical storage tanks. Therefore, a relative risk assessment model based on set pair analysis was established in this paper. According to the characteristic of storage quantity real-time variation, a program is developed to simulate the different scenarios of chemical storage tank leakage and evaluate their relative risks real-timely. The practical problems solved in this study include: (1) identify and quantify the derivative accidents of chemical storage tank leakage, (2) construct the risk assessment model of chemical storage tank leakage, (3) achieve the real-time relative risk assessment of multi chemical storage tanks. A case simulation of a petrochemical wharf tank zone verifies the effectiveness of the proposed method and the performance of program. Some useful conclusion can be draw as follows:
- This paper presented a real-time relative risk assessment method of chemical storage tanks based on set pair analysis, and the effectiveness of the model were verified by a case simulation.
- The derivative accidents of tank leakage were identified and 3 calculation models were applied to quantify the disastrous consequences. The chemical storage tank leakage risk assessment model was established.
- The risks of chemical storage tanks will change with the variation of storage quantity. When one chemical storage tank happens to change, the relative risks of other storage tanks will also be affected.
- A program developed by LabVIEW can efficiently achieve the chemical storage tank leakage simulation and risk assessment, which can provide references for safety management in petrochemical wharf enterprises.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict interest.
ACKNOWLEDGEMENTS
Declared none.
REFERENCES
| [1] | Zhang, X. M.; Chen, C. Mechanism analysis and risk assessment of escalation scenario in chemical industry zones. Process Saf. Environ. Prot., 2013, 91(s 1-2), 79-85. [http://dx.doi.org/10.1016/j.psep.2012.02.003] |
| [2] | Chang, J.I.; Lin, C.C. A study of storage tank accidents. J. Loss Prev. Process Ind., 2006, 19(1), 51-59. [http://dx.doi.org/10.1016/j.jlp.2005.05.015] |
| [3] | Leur, P.D.; Sayed, T. Development of a road safety risk index. Transp. Res. Rec., 2002, 1784(1), 33-42. [http://dx.doi.org/10.3141/1784-05] |
| [4] | Misra, K.B.; Weber, G.G. A new method for fuzzy fault tree analysis. Microelectron. Reliab., 1989, 29(2), 195-216. [http://dx.doi.org/10.1016/0026-2714(89)90568-4] |
| [5] | Rahman, M.; Heikkilä, A.M.; Hurme, M. Comparison of inherent safety indices in process concept evaluation. J. Loss Prev. Process Ind., 2005, 18(4), 327-334. [http://dx.doi.org/10.1016/j.jlp.2005.06.015] |
| [6] | Zhong, M.D. China Safety Science Journal, 1997, 7(2), 6-9. |
| [7] | Si, H.; Ji, H.; Zeng, X. Quantitative risk assessment model of hazardous chemicals leakage and application. Saf. Sci., 2012, 50(7), 1452-1461. [http://dx.doi.org/10.1016/j.ssci.2012.01.011] |
| [8] | Davies, T.; Harding, A.B.; Mckay, I.P.; Robinson, R.G.; Wilkinson, A. Bund effectiveness in preventing escalation of tank farm fires. Process Saf. Environ. Prot., 1996, 74(2), 88-93. |
| [9] | Spouge, J. New generic leak frequencies for process equipment. Process Saf. Prog., 2005, 24(4), 249-257. [http://dx.doi.org/10.1002/prs.10100] |
| [10] | Yu, L.J.; Duo, Y.Q.; Shi, L.C.; Wei, L.J.; Wu, Z.Z. Method for determinating probabilities of leaks in quantitative risk assessment. J. Saf. Sci. Technol., 2007, 3(6), 27-30. |
| [11] | Rijnmond, O. L. Risk analysis of six potentially hazardous industrial objects in the Rijnmond area, a pilot study: a report to the Rijnmond Public Authority; Springer Netherlands, 1982. [http://dx.doi.org/10.1007/978-94-017-2907-9] |
| [12] | John, S. New generic leak frequencies for process equipment Process Saf. Prog., 2005, 24(4), 249-257. |
| [13] | Crossthwaite, P.J.; Filzatrick, R.D.; Hurst, N.W. Risk Assessment for the siting of developments near liquefied petroleum gas installations. IChemE Sympsium Series No. 110, 1988. |
| [14] | Bai, Y.Z.; Engineer, S.; Wen-Yi, E.D.; Zhi-Feng, E.; Xiang-Di, E.Z. Engineer, Determination of ignition source and ignition probability of leaking accidents in petrochemical processes. China Saf. Sci. J., 2010, 20(1), 61-66. |
| [15] | Raj, P. A physical model and improved experimental data correlation for wind induced flame drag in pool fires. Fire Technol., 2010, 46(46), 579-609. [http://dx.doi.org/10.1007/s10694-009-0107-7] |
| [16] | Tauseef, S.; Abbasi, T.; Abbasi, S. Risks of Fire and Explosion Associated With the Increasing Use of Liquefied Petroleum Gas. J. Fail. Anal. Prev., 2010, 10(4), 322-333. [http://dx.doi.org/10.1007/s11668-010-9360-9] |
| [17] | Zhang, Q.L.; Dai, Y.R.; Wang, J.; Zhao, R.Y. Research of Toxic Gas Diffusion Simulation Technology Based on Arc Engine; Springer Berlin Heidelberg, 2013, pp. 35-41. [http://dx.doi.org/10.1007/978-3-642-35470-0_5] |
| [18] | Zhang, H.F. Emergency response poket manual for highly hazardous chemicals; China Petrochemical Press, 2006. |
| [19] | Kang, J.; Liang, W.; Zhang, L.; Lu, Z.; Liu, D.; Yin, W.; Zhang, G. A new risk evaluation method for oil storage tank zones based on the theory of two types of hazards. J. Loss Prev. Process Ind., 2014, 29(1), 267-276. [http://dx.doi.org/10.1016/j.jlp.2014.03.007] |