- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Mechanical Engineering Journal
(Discontinued)
ISSN: 1874-155X ― Volume 14, 2020
Lay-up Optimization of Laminated Composites Using a Modified Branch and Bound Method
Giacomo Canale1, Paul M. Weaver2, Felice Rubino3, *, Angelo Maligno3, Roberto Citarella4
Abstract
Background:
Composite materials are widely used in the aerospace, marine and automotive industries. One of their main advantages is that their stacking sequence can be tailored to maximise/minimise a specific structural performance. Efficient and non-computational-expensive algorithms are always needed to find the optimum stacking sequence of a composite laminate whose thickness is either to be minimised or may be kept constant (i.e. the thickness and the plies orientation percentages are pre-determined; the problem of the optimisation is therefore permutational).
Objective:
A modified branch and bound algorithm is proposed here and used to determine the stacking sequence for single and multi-objective optimisation problems. Laminate thickness and orientation percentages are either variables or determined a priori (the optimisation problem is therefore permutational). Computational time is drastically reduced when compared with other meta-heuristic techniques.
Methods:
The proposed method is a branch and bound algorithm, modified from the original work proposed by Kim and Hwang [10]. The main novelty is the starting point of the optimisation sequence: a laminate formed by “Ideal” layers, described in this paper.
Results:
The modified branch and bound has been first tested with a laminate having fixed thickness and a fixed percentage of layer orientation. Three different problems have been investigated: maximisation of natural frequencies, minimisation of tip deflection and maximisation of buckling critical load. The algorithm has been also tested, secondly, for a problem of weight minimisation subjected to buckling and strength constraints.
Conclusion:
The MBB has been shown to give good fidelity and significant computational advantages compared with a GA. Despite the simplicity of the structures in the numerical examples, it is anticipated that the MBB can be used to determine lay-ups in multi-part structures. The method was used to determine stacking sequences for several problems. The modified branch and bound method was shown to determine good laminate designs and offer significant efficiency savings.
A “Good Design” is here defined as a solution producing “Near Global Optima” fitness values by minimising the computational effort. It was shown that for a single objective without ply competition, global optima were obtained.
Article Information
Identifiers and Pagination:
Year: 2018Volume: 12
First Page: 138
Last Page: 150
Publisher Id: TOMEJ-12-138
DOI: 10.2174/1874155X01812010138
Article History:
Received Date: 01/02/2018Revision Received Date: 15/05/2018
Acceptance Date: 21/05/2018
Electronic publication date: 20/06/2018
Collection year: 2018
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: (https://creativecommons.org/licenses/by/4.0/legalcode). This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
* Address correspondence to this author at the Institute for Innovation in Sustainable Engineering, University of Derby, Quaker Way, Derby DE1 3EE, UK, Tel: 01332593554; E-mails: f.rubino@derby.ac.uk; frubino@unisa.it
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 01-02-2018 |
Original Manuscript | Lay-up Optimization of Laminated Composites Using a Modified Branch and Bound Method | |
1. INTRODUCTION
The success of composite materials has been well documented in recent years [1S.W. Tsai, and N.J. Pagano, Invariant Properties of Composite Materials. Composite., Defense Technical Information Center: Westport, Connecticut, ., 2G. Canale, F. Rubino, P.M. Weaver, R. Citarella, and A. Maligno, "Simplified and accurate stiffness of prismatic and anisotropic Thin-Walled box", Open Mech. Eng. J., vol. 12, pp. 1-20.
[http://dx.doi.org/10.2174/1874155X01812010001] ]. Despite their success and insertion in high profile aircraft, significant efficiency and functionality gains may be obtained by undertaking stacking sequence (lay-up) optimization. Studies have shown that significant weight savings and performance gains can be achieved via lay-up optimization [3M.W. Bloomfield, J.E. Herencia, and P.M. Weaver, "Optimization of anisotropic composite plates incorporating Non-Conventional ply orientations", In: 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference., Apr. 7-10, Schaumburg, IL, 2008.-5J.E. Herencia, P.M. Weaver, and M.I. Friswell, "Initial sizing optimisation of anisotropic composite panels with T-shaped stiffeners", Thin-walled Struct., vol. 46, no. 4, pp. 399-412.
[http://dx.doi.org/10.1016/j.tws.2007.09.003] ].
In lay-up optimization, the design variables are generally ply thickness and ply orientation. In many practical applications, ply thickness is fixed and ply orientations take a range of discrete values. If ply orientations are used as design variables, the resulting response surface is non-convex. As such, gradient-based methods are not entirely reliable optimizers. Motivated by this deficiency, several heuristic and deterministic methods have been used to determine laminate stacking sequences. With respect to heuristic optimizers, the success of a Genetic Algorithm (GA) has been well documented [4J.E. Herencia, P.M. Weaver, and M.I. Friswell, "Optimization of long anisotropic laminated fiber composite panels with T-Shaped stiffeners", AIAA J., vol. 45, no. 10, pp. 2497-2509.
[http://dx.doi.org/10.2514/1.26321] , 5J.E. Herencia, P.M. Weaver, and M.I. Friswell, "Initial sizing optimisation of anisotropic composite panels with T-shaped stiffeners", Thin-walled Struct., vol. 46, no. 4, pp. 399-412.
[http://dx.doi.org/10.1016/j.tws.2007.09.003] ]. Bloomfield et al. [6M.W. Bloomfield, J.E. Herencia, and P.M. Weaver, "Analysis and benchmarking of meta-heuristic techniques for lay-up optimization", Comput. Struc., vol. 88, pp. 272-282.
[http://dx.doi.org/10.1016/j.compstruc.2009.10.007] ] compared three popular techniques for stacking sequence optimization, GA, Particle Swarm Optimization (PSO) and Ant Colony Optimization (ACO). The research indicated that all three methods were suitable optimizers, yet for different problems, different optimizers may be more appropriate. Furthermore, Bloomfield et al. [6M.W. Bloomfield, J.E. Herencia, and P.M. Weaver, "Analysis and benchmarking of meta-heuristic techniques for lay-up optimization", Comput. Struc., vol. 88, pp. 272-282.
[http://dx.doi.org/10.1016/j.compstruc.2009.10.007] ] observed that ACO and PSO could offer significant efficiency savings over a GA. With respect to deterministic optimizers, a branch and bound method has been proposed, chiefly by Todoroki et al. [7A. Todoroki, and Y. Terada, "Improved fractal branch and bound method for stacking-sequence optimizations of laminates", AIAA J., vol. 42, no. 1, pp. 141-148.
[http://dx.doi.org/10.2514/1.9038] , 8M. Sekishiro, and A. Todoroki, "Extended fractal branch and bound method for optimization of multiple stacking sequences of stiffened composite panel", Adv. Compos. Mater., vol. 15, no. 3, pp. 341-356.
[http://dx.doi.org/10.1163/156855106778392098] ]. Todoroki et al. [7A. Todoroki, and Y. Terada, "Improved fractal branch and bound method for stacking-sequence optimizations of laminates", AIAA J., vol. 42, no. 1, pp. 141-148.
[http://dx.doi.org/10.2514/1.9038] , 8M. Sekishiro, and A. Todoroki, "Extended fractal branch and bound method for optimization of multiple stacking sequences of stiffened composite panel", Adv. Compos. Mater., vol. 15, no. 3, pp. 341-356.
[http://dx.doi.org/10.1163/156855106778392098] ] successfully used the branch and bound approach (where the laminate thickness is fixed) for a variety of problems using a single level optimization routine. Despite the apparent success of branch and bound method [9D.R. Morrison, H.J. Sheldon, J.J. Sauppe, and E.C. Sewell, "Branch-and-Bound algorithms: A survey of recent advances in searching, branching and pruning", Discrete Optim., vol. 9, pp. 79-102.
[http://dx.doi.org/10.1016/j.disopt.2016.01.005] ], the algorithm is known to be computationally expensive. This becomes apparent when the set of possible ply orientations or number of plies increases.
It is often desirable to consider the effect of each ply in the lay-up independent of the other plies in the stacking sequence. That is, identification of the ith ply orientation independent of the other i-1 plies. To achieve this, Kim and Hwang [10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554.
[http://dx.doi.org/10.1016/j.compstruc.2005.02.002] ] introduced the concept of an idealized laminate. An idealized laminate is artificially enhanced, which cannot be realized with a real stacking sequence. It is noted, that by utilizing idealized laminae, the effect of each ply in the stacking sequence on the objective function can be quantified. Building upon the concept of an idealized laminate and the branch and bound approach, a two-level optimization is proposed. At the first level of the optimization lamination parameters and plate thickness are used to minimize the mass of the composite plate subject to a set of design constraints, i.e. strength, buckling or aeroelastic constraints. The first level of the optimization is not the focus of the current work, but is detailed in [3M.W. Bloomfield, J.E. Herencia, and P.M. Weaver, "Optimization of anisotropic composite plates incorporating Non-Conventional ply orientations", In: 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference., Apr. 7-10, Schaumburg, IL, 2008.] as part of a two-level approach for lay-up optimisation. However, it is noted that by representing laminate stiffness in terms of lamination parameters, a convex response surface is created which is ably optimised, for lamination parameters and thicknesses, using a gradient-based method. The first level of the optimization established the potential optimal mass (total thickness) and guarantees the existence of a real stacking sequence which satisfies the set of design constraints, and it takes into account conflicting objective or constraint trade-offs. At the second level, a stacking sequence is determined using a discrete optimizer which seeks to maximize (or minimize) a given function or satisfy design constraints depending upon the nature of the problem. Motivated by the efficiency problems of the standard branch and bound algorithm and the work of Kim and Hwang [10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554.
[http://dx.doi.org/10.1016/j.compstruc.2005.02.002] ], a Modified Branch and Bound (MBB) is now proposed. The MBB approach expands the formulation by Kim and Hwan [10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554.
[http://dx.doi.org/10.1016/j.compstruc.2005.02.002] ] to include anisotropic laminates. Furthermore, a modified pruning technique is used to select the ply orientation of each position in the lay-up. This approach yields good designs and offers significant efficiency savings over the conventional branch and bound and other methods such as GA, PSO and ACO. It is shown that by using the MBB with a uni-objective function then global optima are obtained. The novelty of the current work lies in expanding the concept of an idealized laminate and in the introduction of a new and simplified branching and pruning technique compared to the original formulation of Kim and Hwan. This new formulation helps reducing the computational time of more than 10 times when compared to the original algorithm. The proposed modified branch and bound algorithm has been applied to a wide variety of stacking sequence dependent problems in this paper. In addition, a comparison of MBB with GA is provided and discussed to demonstrate the efficacy of the proposed approach.
2. MATERIALS AND METHODS
Kim and Hwang [10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554.
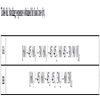
[http://dx.doi.org/10.1016/j.compstruc.2005.02.002] ] defined an ideal lamina to be one with enhanced stiffness, that is practically unachievable, yet relate to the inherent basic ply stiffness. It should be mentioned that the authors restricted their study of ideal laminae to symmetric orthotropic/isotropic laminates. Firstly, the in-plane, coupling and out-of-plane stiffness matrices are defined:
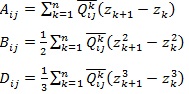 |
(1) |
Where:
n is the number of plies in the lay-up
z is the through thickness co-ordinate, the distance of each layer from the middle plane of the laminate as per classical lamination theory.
Qij are the terms of the reduced in-plane stiffness matrix, characterising the planar behaviour of each ply of the laminate. These terms can be expressed in terms of material invariants as follows:
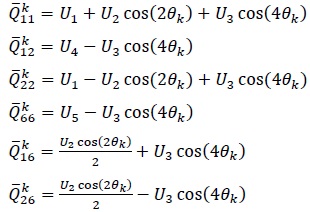 |
(2) |
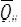 occur at 0, 45, 90, 45, 60, 30 degrees respectively. Clearly, no single ply can take all these orientations at the same time. However, the maximum or ideal
occur at 0, 45, 90, 45, 60, 30 degrees respectively. Clearly, no single ply can take all these orientations at the same time. However, the maximum or ideal
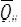 , denoted by,
, denoted by,
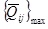 is defined when
is defined when
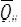 takes its mathematical maximum values simultaneously. In contrast, Kim and Hwang [10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554.
takes its mathematical maximum values simultaneously. In contrast, Kim and Hwang [10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554.[http://dx.doi.org/10.1016/j.compstruc.2005.02.002] ] did not make this definition for
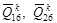 . It is observed that for different problems, different idealizations may be required, i.e. certain stiffness terms may be zero or negative. Moreover, since (2θ) , (4θ )are odd functions, and shear being bi-directional, the minimum of
. It is observed that for different problems, different idealizations may be required, i.e. certain stiffness terms may be zero or negative. Moreover, since (2θ) , (4θ )are odd functions, and shear being bi-directional, the minimum of
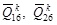 may be required for a particular problem. The angles which minimize the corresponding stiffness terms are readily determined. In stacking sequence optimization, the outer plies often drive the design. This is because of the quadratic and cubic volume fraction effect. For a symmetric laminate, i.e. one which does not exhibit any bending-extension coupling, the D matrix is most influenced by the outermost plies. Hence, for flexural, buckling or natural frequency problems, indeed any problem driven by maximising D matrix considerations, it is important to consider the outermost plies first. Alternatively, if a compliant flexural stiffness is sought, then the innermost plies should be considered first. Therefore, the definition of an ideal laminate proposed by Kim and Hwang [10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554.
may be required for a particular problem. The angles which minimize the corresponding stiffness terms are readily determined. In stacking sequence optimization, the outer plies often drive the design. This is because of the quadratic and cubic volume fraction effect. For a symmetric laminate, i.e. one which does not exhibit any bending-extension coupling, the D matrix is most influenced by the outermost plies. Hence, for flexural, buckling or natural frequency problems, indeed any problem driven by maximising D matrix considerations, it is important to consider the outermost plies first. Alternatively, if a compliant flexural stiffness is sought, then the innermost plies should be considered first. Therefore, the definition of an ideal laminate proposed by Kim and Hwang [10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554.[http://dx.doi.org/10.1016/j.compstruc.2005.02.002] ] is extended to include the above formulation and:
- The fitness (using a defined fitness function) of a potential laminate is maximized for the ideal laminate.
- When a real layer replaces an ideal layer in the ideal lay-up, a lower value of the fitness function is obtained, simply because a real layer is not as stiff as the ideal one. When each ideal layer is subsequently replaced with a real layer (from the outermost ply inwards), the fitness function decreases monotonically with ply position. It is noted that a monotonically sequence which is bounded below, is necessarily convergent. Therefore, the resulting algorithm converges to stable points.
- The change in the fitness function should be quantifiable on a ply-by-ply basis. If the ideal stiffness constants are too large. i.e. excessively values are arbitrarily chosen, changing one ply may not significantly alter the fitness of the laminate. Using Eq. (2) prevents this potential ill-conditioning problem.
- The gradient of the objective function evaluated at the ideal stacking sequence is zero (implying at least local optima).
It is observed that there are potentially different (non-unique) idealizations for different objective functions. This is evident when considering that the optimal angles for a buckling driven problem (typically 45o) differ from the optimum angles from a strength driven problem (typically 0o for axial loading). Therefore, an acceptable laminate idealization must satisfy the aforementioned conditions. This implies that the analysis may have to perform different “Trials and Errors” simulations before finding an ideal layer definition for his specific problem. For complex problems, such like multi-direction loading, the ideal layer may be an “Isotropic” layer whose stiffness and strength cannot be achieved by any existing material or orientation of the available material.
Next, the branch and bound algorithm presented by Kim and Hwang [10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554.
[http://dx.doi.org/10.1016/j.compstruc.2005.02.002] ] is discussed. The first step of their algorithm establishes a random stacking sequence S whose objective function is evaluated. The fitness of S is denoted by F*. Next, the fitness of the ideal stacking sequence, denoted by ID, is evaluated and denoted by FID. Following this step, all of the layers in the ideal laminate are sequentially replaced (from the outermost ply inwards) with real layers until the optimal stacking sequence is determined. Starting from the outermost ply, the ith ideal layer is replaced with the real layer of ply angle θi. During this process, an obtained fitness Fi which is worse than F* need not be branched further. In fact, by replacing ideal layers with real layers, the fitness function necessarily decreases. The branch and bound approach adopted by Kim and Hwang [10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554.
[http://dx.doi.org/10.1016/j.compstruc.2005.02.002] ] is shown in Fig. (1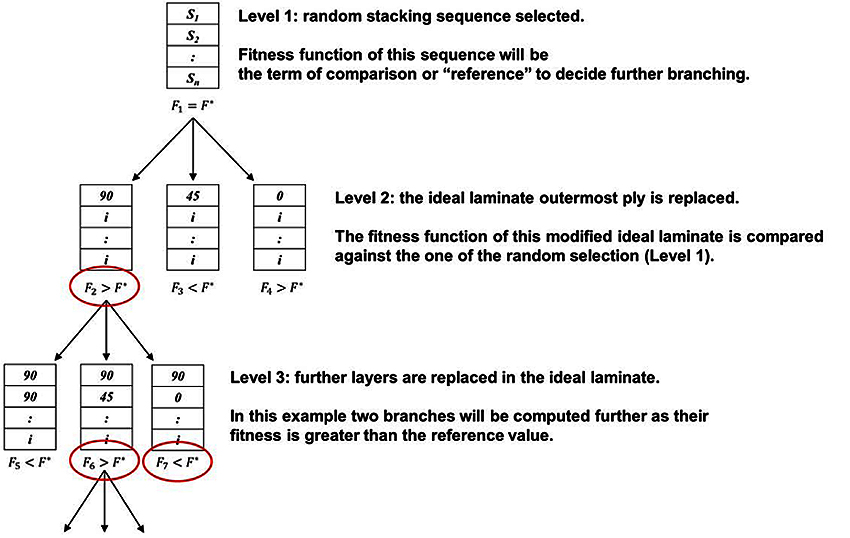 ).
).
 |
Fig. (1) Scheme of Branch and Bound used by Kim and Hwang [10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554. [http://dx.doi.org/10.1016/j.compstruc.2005.02.002] ]. |
It is observed that whilst the full algorithm, proposed by Kim and Hwang [10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554.
[http://dx.doi.org/10.1016/j.compstruc.2005.02.002] ], is able to determine good designs, the resulting algorithm is extremely inefficient. The algorithm proposed by Kim and Hwang [10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554.
[http://dx.doi.org/10.1016/j.compstruc.2005.02.002] ] uses a random initial stacking sequence. In contrast, by using an idealized stacking sequence as a starting point, and changing the ply orientation from the outermost ply inwards, this ensures that the fitness of the laminate monotonically decreases with position. Each ideal layer is replaced with the best real layer with respect to position. Effectively, all branches are pruned except the best and the algorithm continues to the next layer. This pruning mechanism, essentially identifies the largest branch, and is demonstrated in Fig. (2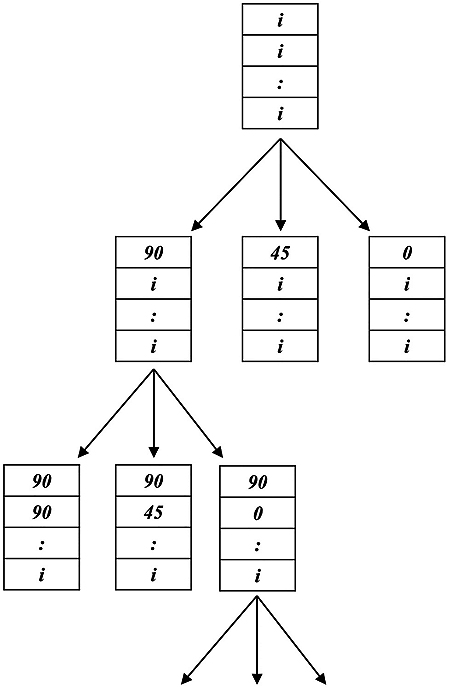 ).
).
 |
Fig. (2) Scheme of modified branch and bound with 3 possible ply orientations [90/45/0]. |
In other words, the MBB here proposed:
- Does not make any use of the initial random stacking sequence but branches the ideal laminate, as the fitness function decreases in value.
- Only the larger branch is identified and computed (each level in which a layer orientation is selected has only 1 solution that will be branched further). If n is the number of layers and m the number of possible orientations, m x n computations are performed.
Using the new branching technique, it is observed that significant efficiency savings can be achieved. Consider, a laminate of n plies, formed from m different ply orientations, there are possible lay-ups. As such, enumeration quickly becomes unviable with a large number of layers, n, due to the combinatorial explosion of possible lay-ups with increasing thickness. If a heuristic search method (such as a GA) is used, the number of evaluations would be r x s, where r is the population size and s is the number of iterations that have taken place until a solution is determined. Using a heuristic approach, r × s < mn. In contrast, the MBB approach evaluates m x n designs. It is observed that this process represents a significant reduction in the number of evaluations.
If there is more than one objective, different ply orientations may compete for the same position. Therefore, additional criteria must be used, in that case, to select the 'Best' ply at each position. Nonetheless, by selecting the 'Best' ply at each position, in multi-objective problems there may be an abundance of possible combinations of stacking sequences which are missed and may yield better results. Despite this potential shortfall, it will be shown, in the next section, that the method is able to determine good designs (near global optima, with a strong reduction of computational time).
3. RESULTS AND DISCUSSION
In this section, several numerical examples are considered. The first set of numerical examples aims to determine a stacking sequence which maximises or minimizes a given objective function for a laminate of fixed thickness and fixed percentages of ply orientations. Take into account that fixing the percentages is equivalent to fixing the in-plane lamination parameters. The following three objectives are considered:
-
Maximize the natural frequency (first mode) of a simply supported rectangular plate. It has been shown [11S. Adali, and V.E. Verijenko, "Optimum stacking sequence design of symmetric hybrid laminates undergoing free vibrations", Compos. Struct., vol. 54, no. 2-3, pp. 131-138.
[http://dx.doi.org/10.1016/S0263-8223(01)00080-0] ], that such analysis could be important in the design of laminates which limit resonance due to external excitation. - Maximize the compression buckling load of a simply supported rectangular plate.
- Minimize the vertical displacements of a clamped laminate subjected to a cantilever tip vertical load.
The second set of numerical examples aims to determine stacking sequences of minimum thickness which satisfy strength and buckling constraints. For each numerical example detailed in this section, the MBB algorithm is used to determine laminate stacking sequences and the results are compared with a permutative GA.
3.1. Maximising the Natural Frequency, Buckling Load and Minimising Vertical Displacement
In the following numerical examples, it is assumed that the laminate is formed from 80 plies. The laminate is assumed to be symmetric with respect to the mid-plane and hence not exhibit any bending-extension coupling. As such, the stacking sequence of 40 plies needs to be determined. Furthermore, the laminate is considered to be balanced in order to not obtain extension-shear coupling. Additionally, the membrane properties of the laminate are fixed, where the laminate has 44% percent of 0 degrees fibres, 22% of 45 degrees fibres, 22% of -45 degrees fibres and 12% of 90 degrees fibres. Hence, there are 16 layers with 0 degrees fibres, 8 layers with 45 degrees fibres, 8 layers with -45 degrees fibres and 8 layers with 90 degrees fibres. The rectangular plate dimensions are 120mm x 40 mm. The material properties of the laminate are shown in Table 1.
The MBB requires the definition of an ideal lamina that satisfies the elastic properties described in section 2. Furthermore, it is assumed that the density of the ideal layer is the same as a real layer. Natural frequencies and compressive buckling loads are evaluated by using a close form solution [12Z. Gürdal, R.T. Hafka, and P. Hajela, Design and Optimization of Laminated Composite Materials., John Wiley & Sons Inc.: New York, .]. The fitness function for the problem of the vertical displacement minimisation under a tip bending load is evaluated by interfacing MATLAB [13 Matlab R2013a. The MathWorks Inc., Natick, Massachusetts, United States., 2013.] and MSC Nastran [14MSC Patran/Nastran Software-MSC Software Corporation, ]. For the permutative GA [15B. Liu, R.T. Haftka, M.A. Akgun, and A. Todoroki, "Permutation genetic algorithm for stacking sequence design of composite laminates", Comput. Methods Appl. Mech. Eng., vol. 186, no. 2-4, pp. 357-372.
[http://dx.doi.org/10.1016/S0045-7825(99)90391-2] ] three tuning parameters must be refined in order to ensure efficient convergence. The following parameters were used in the GA for the maximisation of the compressive buckling load and for the maximisation of the first natural frequency:
- Minimum number of generation before terminations: 80
- Size of initial population: 50
- Number of mutations (permutation of two layers randomly selected): one in a single string of each generation.
Such parameters, for the problem of the minimisation of vertical displacement, since interfacing FEM with Matlab requires more CPU running time, are:
- Minimum number of generation before terminations: 30
- Size of initial population: 20
- Number of mutations (permutation of two layers randomly selected): one in a single string of each generation.
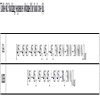
In comparison, it can be observed that the MBB approach requires no such parameters. It is, in fact, a completely deterministic method. A useful way to understand completely how the MBB works is shown in Fig. (3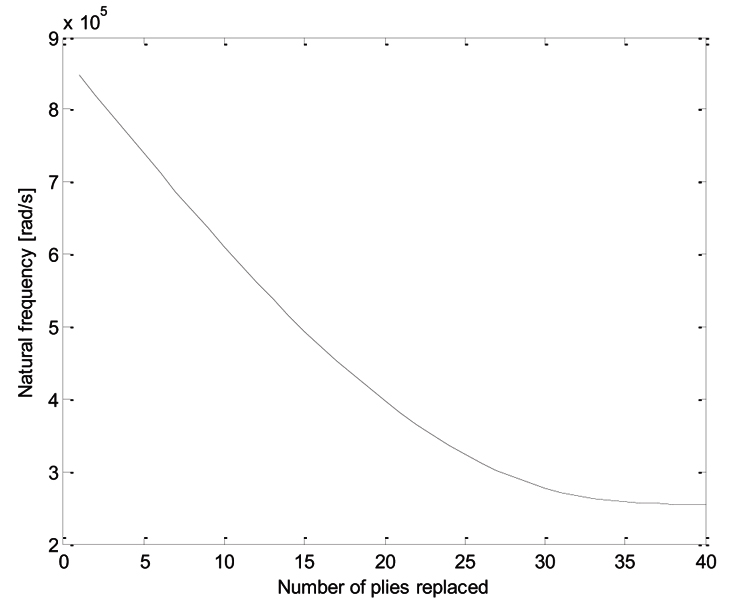 ). The ideal laminate is characterized by the highest value of fitness. As the algorithm proceeds, the value of the fitness decreases monotonically, until the last layer is replaced. With respect to the GA, it was observed that whilst the GA obtained good results, it was only able to find local solutions which may or may not be local minima. For practical considerations, it is useful to include the analysis with the empirical four ply rule [16A. Todoroki, N. Sasada, and M. Miki, "Object-Oriented approach to optimize composite laminated plate stiffness with discrete ply angles", J. Compos. Mater., vol. 30, no. 9, pp. 1020-1041.
). The ideal laminate is characterized by the highest value of fitness. As the algorithm proceeds, the value of the fitness decreases monotonically, until the last layer is replaced. With respect to the GA, it was observed that whilst the GA obtained good results, it was only able to find local solutions which may or may not be local minima. For practical considerations, it is useful to include the analysis with the empirical four ply rule [16A. Todoroki, N. Sasada, and M. Miki, "Object-Oriented approach to optimize composite laminated plate stiffness with discrete ply angles", J. Compos. Mater., vol. 30, no. 9, pp. 1020-1041.
[http://dx.doi.org/10.1177/002199839603000904] ]. Results obtained using MBB with and without the four plies rule are presented, along with results obtained using a GA.
 |
Fig. (3) Natural frequency of the first mode against the number of ideal layers replaced. |
The results for the frequency maximization problem are detailed in Tables 2a and 2b.
The mean fitness of each generation of the population of the GA is shown in Fig. (4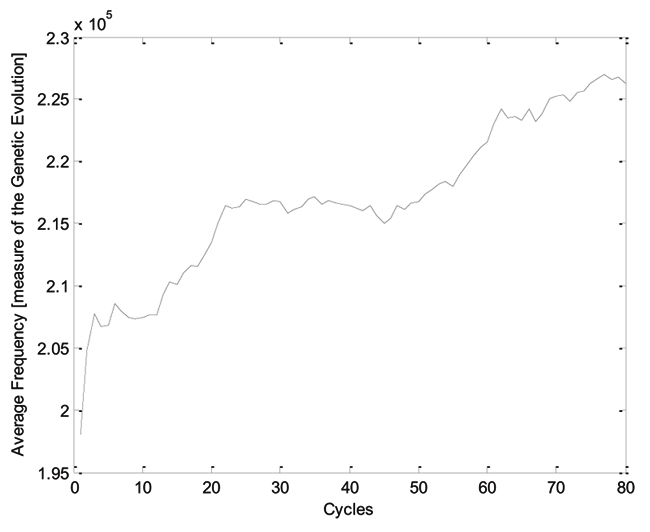 ). Such population is evolving through the generations because the mean value generally increases, even if some oscillations are observed. It proves that the algorithm works correctly.
). Such population is evolving through the generations because the mean value generally increases, even if some oscillations are observed. It proves that the algorithm works correctly.
 |
Fig. (4) Evolution of the mean fitness of the GA population. |
Moreover, a number of 80 generations has been chosen because the algorithm does not need more to reach its convergence: A larger number of cycles will not correspond to any improvement in the population.
Next, both optimization techniques were used to maximize the buckling compression load of a simply supported plate. Results are shown in Tables 3a and 3b.
It is observed that also for this particular problem the MBB gives better results. Moreover, the MBB is quicker and, hence, offers significant efficiency savings. In both cases, the implementation of the four plies rule does not affect the value of the fitness function.
Next, for the vertical displacement minimization problem under a unitary tip load, the obtained stacking sequences are shown in Table (4a) and a comparison of results is presented in Table 4b.
It is observed that the MBB obtains better lay-ups than the GA. The MBB offers also significant efficiency savings over the GA.
As already remarked in this paper, the MBB offers computational time advantage when compared to the original BB proposed in Reference 10T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554.
[http://dx.doi.org/10.1016/j.compstruc.2005.02.002] . The optimum stacking sequence is however the same Tables 2a and 2b, 3a and 3b, 4a and 4b.
3.2. Lay-up Optimisation for Minimum Thickness Subject to Strength and Buckling Constraints
In this section, a different optimization problem is considered. That is, a stacking sequence of minimum thickness is sought which satisfies strength and buckling constraints. To achieve this objective, a two-level optimization approach is used. At the first level, lamination parameters and plate thicknesses are used to minimise the mass of the composite plate subject to strength and buckling constraints [3M.W. Bloomfield, J.E. Herencia, and P.M. Weaver, "Optimization of anisotropic composite plates incorporating Non-Conventional ply orientations", In: 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference., Apr. 7-10, Schaumburg, IL, 2008.].The first level proves the existence of a real stacking sequence and establishes the minimal (continuous) thickness taking into account buckling and strength trade-offs. At the second level, a discrete optimizer is used to determine the laminate stacking sequence which satisfies the set of design constraints. For reasons of brevity, the details concerning the first level of the optimization are not presented here, but can be found in [3M.W. Bloomfield, J.E. Herencia, and P.M. Weaver, "Optimization of anisotropic composite plates incorporating Non-Conventional ply orientations", In: 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference., Apr. 7-10, Schaumburg, IL, 2008.]. In the following numerical examples, several load cases are considered. Furthermore, the set of possible ply orientations are expanded to include 0, 90, 45, -45, 30, -30, 60, -60 degrees. For each case study, four structural problems are considered – each being a simply supported composite plate of 1200mm x 200mm with different loading conditions. The following load cases will be considered:
i) Nx = 0, Nxy = -800 N / mm
ii) Nx = -750, Nxy = 0 N / mm
iii) Nx = -600, Nxy = 300 N / mm
iv) Nx = -200, Nxy = -500 N / mm
It can be observed that a) the loads are representative of those found in a cover skin for an aircraft wing structure and b) all aspect ratios are sufficiently large to allow use of the buckling closed form solutions outlined in [3M.W. Bloomfield, J.E. Herencia, and P.M. Weaver, "Optimization of anisotropic composite plates incorporating Non-Conventional ply orientations", In: 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference., Apr. 7-10, Schaumburg, IL, 2008.]. The shear deformation effects are not considered. Additionally, the material properties used in the optimization are shown in Table 5.
For each load case, the MBB and a GA [6M.W. Bloomfield, J.E. Herencia, and P.M. Weaver, "Analysis and benchmarking of meta-heuristic techniques for lay-up optimization", Comput. Struc., vol. 88, pp. 272-282.
[http://dx.doi.org/10.1016/j.compstruc.2009.10.007] ] were used to determine laminate stacking sequences. In Tables 6a, and 6b stacking sequences and critical reserve factors, determined via the two methods are detailed. Furthermore, the CPU time is shown. As can be seen, the selected idealization is an isotropic laminate which satisfies the criteria for an idealised layer, defined in section 1. Interestingly, by fixing the two outermost plies and assume the inner n-2 plies to be ideal layers, all possible combinations of the first two plies are considered and the objective function evaluated. The results, for an example problem, are visualized in Fig. (5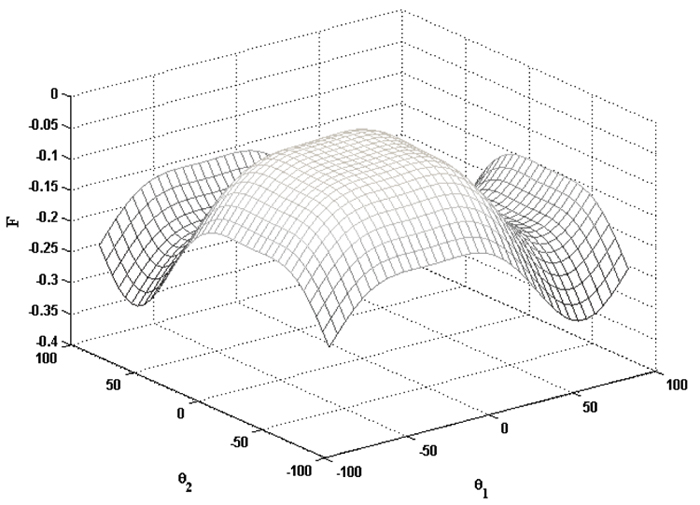 ).
).
 |
Fig. (5) Response surface of the fitness function for the two outermost plies. |
In Fig. (4 ), negative values for F show designs which satisfy the strength and buckling constraints. Therefore, lower values of F correspond to better designs. From Fig. (4
), negative values for F show designs which satisfy the strength and buckling constraints. Therefore, lower values of F correspond to better designs. From Fig. (4 ), it can be seen that the best outer two positions correspond to approximately 60 degrees respectively. The highly non-convex nature of the response surface implies that gradient-based methods would have difficulty in obtaining stacking sequences which satisfy the strength and buckling constraints.
), it can be seen that the best outer two positions correspond to approximately 60 degrees respectively. The highly non-convex nature of the response surface implies that gradient-based methods would have difficulty in obtaining stacking sequences which satisfy the strength and buckling constraints.
From the Tables 6a-6h, it is clear that both algorithms performed well. Generally, the GA obtains slightly higher reserve factors but with a higher associated CPU penalty. When the MBB did not satisfy the design constraints, i.e. for multi-objective problems where ply orientations were competing for the same position, integrating the algorithm with a heuristic optimiser may yield better reserve factors and still reduce the overall running time of the optimization (compared to a single heuristic based approach).
CONCLUSION
The MBB has been shown to give good fidelity and significant computational advantages compared with a GA. Despite the simplicity of the structures in the numerical examples, it is anticipated that the MBB can be used to determine lay-ups in multi-part structures.
The method was used to determine stacking sequences for several problems. The modified branch and bound method was shown to determine good laminate designs and offer significant efficiency savings. It was shown that for a single objective without ply competition, global optima were obtained. However, for multi-objective or multi-criteria problems, different ply orientations may compete for the same ply position. This competition is evident when considering the optimal angles for buckling or the optimum angles for strength driven designs. By selecting only the best ply for a given position there may be an abundance of possible combinations of angles missed which may give improved designs.Obtained designs, which do not have reserve factors greater or equal to one or satisfy some given criteria, could form a part of an initial population of a heuristic method. In addition, it is believed that the method can be applied to determine lay-ups in multi-part structures, a topic of future interest.
NOMENCLATURE
| Aij | = Components of The In-Plane Stiffness Matrix |
| Bij | = Components of The Coupling Stiffness Matrix |
| Dij | = Components of The Out-of-Plane Stiffness Matrix |
| E11, E22 | = Longitudinal and Transverse Young's Moduli |
| F | = Fitness Function |
| G12 | = Shear Modulus |
| Nx | = Axial Force Per Unit of Length |
| Nxy | = Shear Force Per Unit of Length |
| Qij | = Components of the Reduced Stiffness Matrix |
| s | = Symmetric |
| Ui | = Material Invariants |
| ρ | = Density of Material |
| ν12 | = Poisson’s Ratio |
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
Declared none.
REFERENCES
| [1] | S.W. Tsai, and N.J. Pagano, Invariant Properties of Composite Materials. Composite., Defense Technical Information Center: Westport, Connecticut, . |
| [2] | G. Canale, F. Rubino, P.M. Weaver, R. Citarella, and A. Maligno, "Simplified and accurate stiffness of prismatic and anisotropic Thin-Walled box", Open Mech. Eng. J., vol. 12, pp. 1-20. [http://dx.doi.org/10.2174/1874155X01812010001] |
| [3] | M.W. Bloomfield, J.E. Herencia, and P.M. Weaver, "Optimization of anisotropic composite plates incorporating Non-Conventional ply orientations", In: 49th AIAA/ASME/ASCE/AHS/ASC Structures, Structural Dynamics, and Materials Conference., Apr. 7-10, Schaumburg, IL, 2008. |
| [4] | J.E. Herencia, P.M. Weaver, and M.I. Friswell, "Optimization of long anisotropic laminated fiber composite panels with T-Shaped stiffeners", AIAA J., vol. 45, no. 10, pp. 2497-2509. [http://dx.doi.org/10.2514/1.26321] |
| [5] | J.E. Herencia, P.M. Weaver, and M.I. Friswell, "Initial sizing optimisation of anisotropic composite panels with T-shaped stiffeners", Thin-walled Struct., vol. 46, no. 4, pp. 399-412. [http://dx.doi.org/10.1016/j.tws.2007.09.003] |
| [6] | M.W. Bloomfield, J.E. Herencia, and P.M. Weaver, "Analysis and benchmarking of meta-heuristic techniques for lay-up optimization", Comput. Struc., vol. 88, pp. 272-282. [http://dx.doi.org/10.1016/j.compstruc.2009.10.007] |
| [7] | A. Todoroki, and Y. Terada, "Improved fractal branch and bound method for stacking-sequence optimizations of laminates", AIAA J., vol. 42, no. 1, pp. 141-148. [http://dx.doi.org/10.2514/1.9038] |
| [8] | M. Sekishiro, and A. Todoroki, "Extended fractal branch and bound method for optimization of multiple stacking sequences of stiffened composite panel", Adv. Compos. Mater., vol. 15, no. 3, pp. 341-356. [http://dx.doi.org/10.1163/156855106778392098] |
| [9] | D.R. Morrison, H.J. Sheldon, J.J. Sauppe, and E.C. Sewell, "Branch-and-Bound algorithms: A survey of recent advances in searching, branching and pruning", Discrete Optim., vol. 9, pp. 79-102. [http://dx.doi.org/10.1016/j.disopt.2016.01.005] |
| [10] | T. Kim, and I.H. Hwang, "Optimal design of composite wing subjected to gust loads", Comput. Struc., vol. 83, no. 19-20, pp. 1546-1554. [http://dx.doi.org/10.1016/j.compstruc.2005.02.002] |
| [11] | S. Adali, and V.E. Verijenko, "Optimum stacking sequence design of symmetric hybrid laminates undergoing free vibrations", Compos. Struct., vol. 54, no. 2-3, pp. 131-138. [http://dx.doi.org/10.1016/S0263-8223(01)00080-0] |
| [12] | Z. Gürdal, R.T. Hafka, and P. Hajela, Design and Optimization of Laminated Composite Materials., John Wiley & Sons Inc.: New York, . |
| [13] | Matlab R2013a. The MathWorks Inc., Natick, Massachusetts, United States., 2013. |
| [14] | MSC Patran/Nastran Software-MSC Software Corporation, |
| [15] | B. Liu, R.T. Haftka, M.A. Akgun, and A. Todoroki, "Permutation genetic algorithm for stacking sequence design of composite laminates", Comput. Methods Appl. Mech. Eng., vol. 186, no. 2-4, pp. 357-372. [http://dx.doi.org/10.1016/S0045-7825(99)90391-2] |
| [16] | A. Todoroki, N. Sasada, and M. Miki, "Object-Oriented approach to optimize composite laminated plate stiffness with discrete ply angles", J. Compos. Mater., vol. 30, no. 9, pp. 1020-1041. [http://dx.doi.org/10.1177/002199839603000904] |