- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Petroleum Engineering Journal
(Discontinued)
ISSN: 1874-8341 ― Volume 12, 2019
Fuzzy Logic in Carbonate Reservoir Quality Assessment: A Case Study from Tarim Basin, China
Weifu Liu*
Abstract
Introduction:
To address reservoir quality assessment in highly complex and heterogeneous carbonate reservoirs, a methodology utilizing fuzzy logic is developed and presented in this paper. Based on carbonate reservoir characteristics, three parameters reflecting the macroscopic and microscopic of storage abundance, permeability, and median of pore throat radius were selected to establish the factor set and the evaluation criteria. After analysis of core and test data, a membership function is constructed by semi-drop trapezoid method and the weight formula is also determined by reservoir factor sub-index. The developed method then is used to evaluate a carbonate reservoir in the Tarim Basin in China. Based on the result of single well evaluation, the plane classification map of the carbonate reservoir quality is constructed. Results obtained from reservoir quality assessment in the K32 well show that I-level, II-level, and III-level reservoir qualities account for 58%, 37%, 5% of the reservoir, respectively. The results are consistent with the actual production data demonstrating reliability of the proposed method for reservoir quality assessment practices in usually very complex and heterogeneous carbonate reservoirs.
Background:
Carbonate reservoirs are complex and heterogeneous and this makes their evaluation a difficult task.
Objective:
To overcome the uncertainties associated with evaluation of complex carbonate reservoirs a reliable method to accurately evaluate carbonate reservoirs is presented.
Methods:
Fuzzy logic is used to evaluate a carbonate reservoir from Tarim Basin in China. Based on carbonate reservoir characteristics, three parameters reflecting the macroscopic and microscopic of storage abundance, permeability, and median of pore throat radius are selected to establish the factor set and to evaluate the criteria of carbonate reservoir. After the analysis of core and test data, a membership function is reasonably constructed by semi-drop trapezoid method and the weight formula is also determined by reservoir factor sub-index.
Results:
An effective methodology for the evaluation of reservoir quality in carbonate reservoirs is established by using fuzzy logic. In addition, an example reservoir from China is used to demonstrate the applicability of the developed method.
Conclusion:
Based on the result of single well evaluation, the plane classification map of the carbonate reservoir is constructed. Favorable zones in the reservoir are also delineated. Evaluation results are consistent with the actual production data of gas and oil which proves that the proposed method is instrumental in reservoir quality assessment.
Article Information
Identifiers and Pagination:
Year: 2017Volume: 10
First Page: 195
Last Page: 203
Publisher Id: TOPEJ-10-195
DOI: 10.2174/1874834101710010195
Article History:
Received Date: 14/01/2017Revision Received Date: 13/04/2017
Acceptance Date: 15/05/2017
Electronic publication date: 12/10/2017
Collection year: 2017
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
* Address correspondence to this author at the College of Geosciences, Northeast Petroleum University, Daqing Heilongjiang, 163318, China; Tel: +86 13804651715; Fax: +86 0459 6504707; E-mail: liuwfdq@163.com
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 14-01-2017 |
Original Manuscript | Fuzzy Logic in Carbonate Reservoir Quality Assessment: A Case Study from Tarim Basin, China | |
1. INTRODUCTION
Due to the complexity and heterogeneity of carbonate reservoirs, adequate reservoir evaluation is always a difficult problem. At present, carbonate reservoir evaluation is mainly a single factor evaluation method or multi factor scoring method, but there are limitations [1W.F. Liu, "Fuzzy comprehensive evaluation of carbonate reservoir", J. Inf. Comput. Sci., vol. 12, no. 10, pp. 3819-3826, 2015.
[http://dx.doi.org/10.12733/jics20106042] , 2Q.Y. Miao, X.M. Zhu, H.M. Guo, and H. Zhao, "Log evaluation of complex carbonate reservoirs in centre block of the eastern margin of Pre-caspian Basin", Well Logging Technol, vol. 38, no. 2, pp. 196-200, 2014.]. The single factor evaluation method cannot accurately represent the characteristics of carbonate reservoirs. Multi factor scoring method is also prone to conflict and evaluation result is not very clear [3B.K. Shen, D.W. Xue, J.Y. Zhao, and Y.D. Shen, "The logging evaluating method on carbonates reservoirs", Prog. Geophysiscs, vol. 39, no. 1, pp. 261-270, 2014., 4T.J. Li, D.L. Guo, Y.J. Gong, and Z.H. Tang, "A research of fuzzy comprehensive evaluation on carbonate reservoir", Fuzzy Eng. Oper. Res., vol. 147, pp. 331-337, 2012.
[http://dx.doi.org/10.1007/978-3-642-28592-9_34] ]. To overcome these issues in way of adequate reservoir quality assessment mainly caused by uncertainties associated with the reservoir geology fuzzy logic is used to develop an effective method for reservoir quality assessment in carbonate reservoirs. Fuzzy mathematics is not binary logic, but fuzzy logic for analysis and reasoning. It is not the absolute “zero” or the absolute “one”, but the interval between “zero” and “one”. The process of knowing the geological problem is similar. In accordance with this logic, the principle of merit can be used to make judgments. Fuzzy mathematics in reservoir evaluation can accurately evaluate the corresponding reservoirs, and objectively reveal the original distribution of characteristics of carbonate reservoirs. It also provides a new method for the carbonate reservoir evaluation.
The Middle Ordovician Carbonate Reservoir is the main target stratum of oil and gas exploration and development in the new area of the Middle Tarim Basin in China. It is comprised of shallow marine sediments mainly composed of limestone, dolomite, dolomitic limestone, and dolomite. The carbonate reservoir is very heterogeneous because of tidal effects and also diagenesis. At present, the type of distribution of reservoir parameters is not clear affecting the optimum development of the reservoir [5Z.Q. Gao, Z.B. Liu, and S.L. Gao, "Characteristics and genetic models of lower Ordovician carbonate reservoirs in Southwest Tarim Basin, NW China", J. Petrol. Sci. Eng., vol. 144, pp. 99-112, 2016.
[http://dx.doi.org/10.1016/j.petrol.2016.03.007] , 6H. Pang, J.P. Chen, and X.Q. Pang, "Key factors controlling hydrocarbon accumulations in Ordovician carbonate reservoirs in the Tazhong area, Tarim basin, western China", Mar. Pet. Geol., vol. 43, pp. 88-101, 2013.
[http://dx.doi.org/10.1016/j.marpetgeo.2013.03.002] ]. Due to the combined effect of sedimentation, diagenesis, and tectonics, the reservoir space type, the micro and pore structure and the physical properties vary a lot which leads to huge uncertainties in reservoir quality assessment.
Effectively integration of these factors and objective evaluation of the reservoir are the key elements in determining favorable zones (high quality) in the reservoir. In this paper, fuzzy logic is used to quantitatively evaluate quality of a heterogeneous and complex carbonate reservoir from China. Parameters such as storage abundance, permeability, and median of pore-throat-radius are selected which reflect the microscopic and macroscopic characteristics of the reservoir. This can help to improve the development and management strategy of the reservoir. Well data were used in evaluation of theI-level and II-level reservoirs and the results are compared to the production data. Optimal development of carbonate reservoirs is demonstrated via evaluation of a carbonate reservoir from Tarim Basin in China using the proposed method.
2. METHODOLOGY
2.1. Fuzzy Logic in Reservoir Evaluation
Fuzzy logic only takes 0 or 1 of the specific function in the ordinary set, promotes the (0, 1) interval to obtain the membership function. The membership function is a generalization of the indicator function in a fuzzy set. In fuzzy logic, it represents the degree of truth as an extension of valuation. Degrees of truth are often confused with probabilities, although they are conceptually distinct, because fuzzy truth represents membership in vaguely defined sets, no likelihood of some event or condition. It is the absolute belonging or not belonging to the gradual expansion of flexible relationship [7B. Li, and L. Xu, "Risk assessment of ground water inrush from underlying aquifers based on fuzzy comprehensive evaluation and its application", Open Fuels & Energy Sci. J, vol. 7, pp. 107-112, 2014.
[http://dx.doi.org/10.2174/1876973X01407010107] -9H.C. Liao, Z.S. Xu, X.J. Zeng, and D.L. Xu, "An enhanced consensus reaching process in group decision making with intuitionistic fuzzy preference relations", Inf. Sci., vol. 329, pp. 274-286, 2016.
[http://dx.doi.org/10.1016/j.ins.2015.09.024] ]. Thus, the mathematical methods to deal with the fuzzy concept of the middle transition are very convenient. Because of the uncertainty of fuzzy mathematics, it can determine the occurrence of the event or not. Therefore, it has the advantage of comprehensive evaluation in complex carbonate reservoirs. Carbonate reservoirs are complex and heterogeneous. Fuzzy mathematics can overcome many uncertain factors in the process of reservoir evaluation. As a result, the fuzzy method of reservoir evaluation can be more objective method for evaluation of complex and heterogeneous carbonate reservoirs and finding adequate distribution of reservoir parameters.
According to the principle of fuzzy mathematics, the evaluation model for carbonate reservoirs is established which is composed of three element sets including factors set, evaluation set, and weight set.
Factors set U:
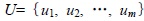 |
(1) |
Where um is the m-th evaluation factor.
Evaluation set V:
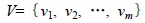 |
(2) |
Where vm is the m-th judging level of evaluation factor.
Weight set A:
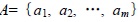 |
(3) |
Where am is the m-th Weight of the evaluation factor.
To make sure all the factors play a role in reservoir evaluation, the relationship between the factor set U and the evaluation set V is established. Definition fuzzy mapping R from the factor set U to the evaluation set V is a transformation matrix of the reservoir evaluation. The transformation matrix R is as follows:
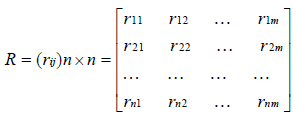 |
(4) |
Where rij is the membership degree of the i-th factor of the j-th evaluation level. Then, the weight set matrix A by the role of various factors in comprehensive reservoir evaluation and the transformation matrix R of the comprehensive reservoir evaluation are synthesized by fuzzy transformation and the comprehensive reservoir evaluation matrix is obtained:
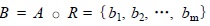 |
(5) |
Where B is the evaluation grade of V on rank fuzzy subsets, “○” is the fuzzy operator of two fuzzy matrixes [15H. Dong, L.X. Wei, and Q.N. Wang, "A study on oil pipeline risk assessment technique based on fuzzy analytic hierarchy process", Open Pet. Eng. J., vol. 7, pp. 125-129, 2014.
[http://dx.doi.org/10.2174/1874834101407010125] ], bm is rank vm comprehensive evaluation of the reservoir level of the resulting fuzzy subset B of a membership. On the basis of the maximum membership principle, the level vi of the maximum bi is chosen as the result of the comprehensive reservoir evaluation. Here, the choice evaluation parameter, the structure membership function, and the determination weight are the key factors in carbonate reservoir evaluation with fuzzy mathematics.
2.2. Parameters Evaluation and Selection
Because of complex nature of carbonate reservoirs, the factors that affect the productivity of oil and gas wells in the study area are analyzed comprehensively. The parameters which are the most closely related to the carbonate reservoir are selected as the index of comprehensive reservoir evaluation. According to the analysis of carbonate reservoirs in Middle Ordovician of Middle Tarim Basin, three parameters reflecting the macroscopic and microscopic characteristics of storage abundance, permeability, and median pore throat radius were selected. Storage abundance reflects the reserves capacity of the carbonate reservoirs. Permeability reflects the carbonate reservoir’s ability to conduct fluids. Median pore throat radius reflects the microscopic pore structure and pore throat size of the carbonate reservoir. These three parameters constitute a set of factors which can provide an accurate and proper understanding of characteristics of the carbonate reservoirs in the study area.
Because of the scattered distribution of the data there is high variance in the database. If the original data is directly used, the role of the orders of magnitude larger of indicators will be highlighted, and the role of the orders of magnitude smaller of highly sensitive indicators will be weakened. Therefore, it is necessary to normalize the original data [10M. Abdolreza, and T.M. Reza, "Cooperative spectrum sensing using fuzzy membership function of energy statistics", Int. J. Electron Commun., vol. 70, no. 3, pp. 234-240, 2016.
[http://dx.doi.org/10.1016/j.aeue.2015.11.005] -12A. Rami, M.D. Kudret, and K.G. Suresh, "Coping with uncertainties in production planning through fuzzy mathematical programming: application to steel rolling industry", Int. J. Oper. Res., vol. 22, no. 1, pp. 1-30, 2015.
[http://dx.doi.org/10.1504/IJOR.2015.065937] ], which can be normalized to the same range. The normalization formula is as follows:
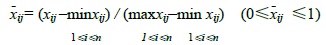 |
(6) |
Where
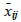 is the data after normalization, xij is the j-th parameter of the i-th sample in the original data, n is the total number of samples.
is the data after normalization, xij is the j-th parameter of the i-th sample in the original data, n is the total number of samples.
2.3. Structure Membership Function
How to construct the expression of the membership function is a theoretical problem that has not been solved by the fuzzy mathematics yet. After statistical analysis and preprocessing of the reservoir evaluation parameters of the study area, semi-drop trapezoid method is adopted to construct membership function of the three selected evaluation indexes to establish three evaluation grades for reservoirs: I-level reservoir, II-level reservoir, and III-level reservoir. The formula is as follows:
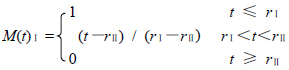 |
(7) |
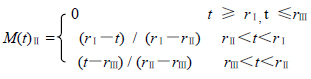 |
(8) |
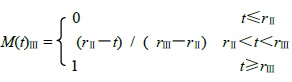 |
(9) |
Where t is the actual value of the evaluation parameter. rI, rII and rIII are the standard values of the comprehensive reservoir evaluation of I-level reservoir, II-level reservoir, and III-level reservoir. Thus, the membership function values of the evaluation factors are obtained.
2.4. Determination of the Weight of Fuzzy Sets
The weight reflects the role of the evaluation factors in the comprehensive reservoir evaluation. At present, in practical application, the weight uses the scoring method [13L. Xu, K. Zhu, and X.L. Yang, "Production forecasting of coalbed methane wells based on type-2 fuzzy logic system", Open Pet. Eng. J,, vol. 9, pp. 268-278, 2016.
[http://dx.doi.org/10.2174/1874834101609010268] -15H. Dong, L.X. Wei, and Q.N. Wang, "A study on oil pipeline risk assessment technique based on fuzzy analytic hierarchy process", Open Pet. Eng. J., vol. 7, pp. 125-129, 2014.
[http://dx.doi.org/10.2174/1874834101407010125] ]. To avoid the influence of subjective factors based on the statistics of the actual data in the study area reservoir factor sub-indexes are used to quantitatively determine the weights of fuzzy sets. The determined weights of the fuzzy sets are then used to weight the correlation coefficient between one factor and other factors. The calculation formula is as follows:
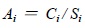 |
(10) |
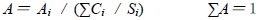 |
(11) |
Where Ai is the i-th weight value of the reservoir evaluation factor, Ci is the i-th actual value of the reservoir evaluation factor, Si is the i-th weighted average value of three standard levels of reservoir evaluation factor, A is the weight set of the reservoir evaluation factor. After each individual weight value standard, the weight value is limited to (0, 1). Thus, 3 evaluation indexes are obtained, which are composed of 1×3 order weight matrix A.
3. RESERVOIR EVALUATION RESULTS
Based on the above ideas and fuzzy logic method of evaluation of carbonate reservoirs, the Middle Ordovician carbonate reservoir in Middle Tarim Basin is used as an example.
3.1. Establishment of Factor Set and Evaluation Set
The factor set of the evaluation object is established after stepwise regression analysis:
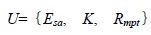 |
(12) |
Where Esa is the storage abundance, K is the permeability, Rmpt is the median pore throat radius.
Taking the K32 well as an example, the actual value of the reservoir parameters shows that the reservoir energy abundance is 0.57 m2, the permeability is 8.6×10-3 μm2, and the median pore throat radius is 0.53 μm. The factor set is constructed:
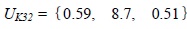 |
(13) |
According to the characteristics of the carbonate reservoir in Middle Ordovician of middle Tarim area, the corresponding evaluation set is established:
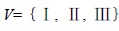 |
(14) |
Carbonate reservoir evaluation standards of the three parameters for the studied reservoir are presented in Table (1). Based on the analysis of core and test data of the carbonate reservoir, the carbonate reservoir is divided into three levels in terms of reservoir quality: I-level reservoir as good quality reservoir, II-level reservoir as medium quality reservoir, and III-level as poor quality reservoir.
3.2. Formation of Fuzzy Relational Matrix
Based on the evaluation standards presented in Table (1), the actual parameter values used to constitute the factor set UK32 are substituted in equations (7), (8) and (9) to determine the evaluation set V. The membership function value of comprehensive reservoir evaluation for each single factor is then obtained. From this, the transformation matrix RK32 of K32 well is derived:
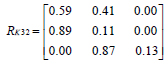 |
(15) |
In the same way, the transformation matrix of the other wells can be calculated.
3.3. Weight Set Determination
The weight should reflect the difference in material property and the difference between people's understanding weight or importance of different parameters. The weight value is calculated using equations (10) and (11) and the weight set is determined by the weight of each factor. Weight values for the K32 well are presented in Table (2). Thereby, the weight set of K32 wells is determined as the following:
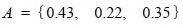 |
(16) |
3.4. Reservoir Quality Evaluation
After the calculation of R and A, the results are obtained by the formula (5). The level of quality of the carbonate reservoir is evaluated according to the principle of maximum membership degree. The transformation matrix R by the single factor membership function values obtained and the weight set A by weight value of each single factor obtained for K32 well and then substituted into the formula (5) to get the fuzzy matrix. Using the fuzzy synthetic operator comprehensive evaluation of the carbonate reservoir quality in K32 is conducted:
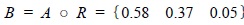 |
(17) |
Results obtained from reservoir quality assessment in the K32 well shows that I-level, II-level, and III-level reservoir qualities account for 58%, 37%, 5%, respectively. Depending on the principle of the maximum membership, the evaluation result of K32 well is I-level reservoir distribution area. In a same way, the results of reservoir comprehensive evaluation in other wells can be obtained.
The results obtained from comprehensive reservoir evaluation of representative wells of K17, K22, K32, K46, K53, and K67 in Middle Ordovician of middle Tarim area are presented in Table (3). The evaluation results are used to prepare a contour map for each level and different levels of regions are delineated. Figs. (1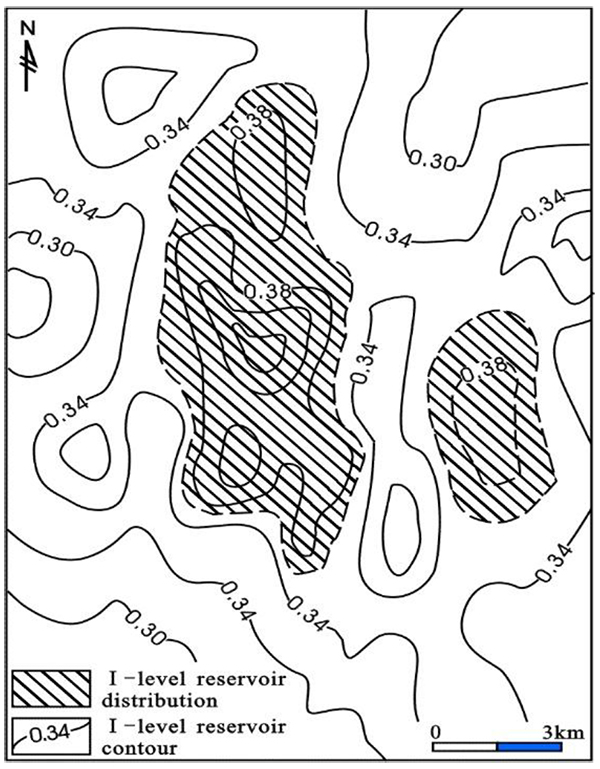 to 3
to 3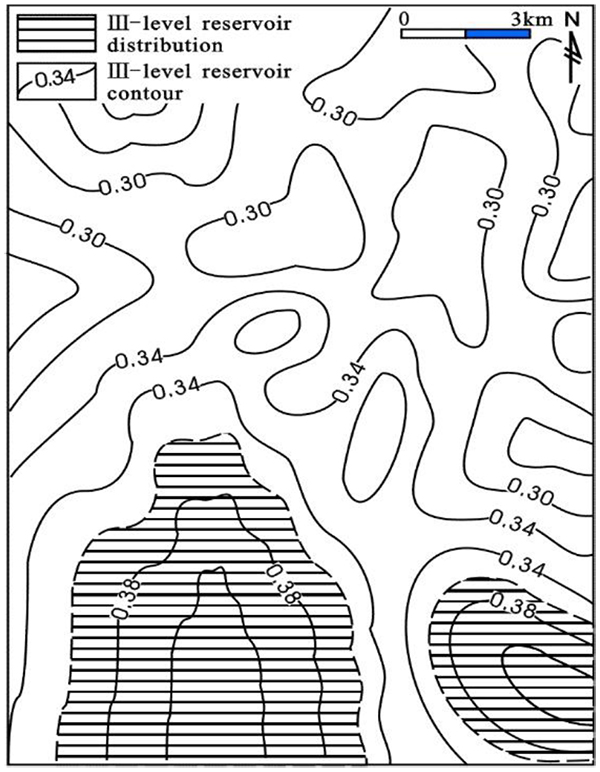 ) show the I-level, II-level, and III-level reservoir qualities in the study area, respectively.
) show the I-level, II-level, and III-level reservoir qualities in the study area, respectively.
 |
Fig. (1) I-level reservoir distribution of reservoir evaluation in Middle Ordovician, contour for I-level reservoir, filling graphical range for I-level reservoir. |
 |
Fig. (2) II-level reservoir distribution of reservoir evaluation in Middle Ordovician, contour for II-level reservoir, filling graphical range for II-level reservoir. |
 |
Fig. (3) III-level reservoir distribution of reservoir evaluation in Middle Ordovician, contour for III-level reservoir, filling graphical range for III-level reservoir. |
4. DISCUSSION
Fuzzy logic reservoir evaluation can effectively integrate various reservoir parameters to avoid the uniqueness and inconsistency of single index evaluation method. The results of quantitative evaluation of carbonate reservoirs compare with the actual reservoir capacity in a Middle Ordovician Carbonate Reservoir in the middle Tarim Basin, in China. Representative production data is presented in Fig. (4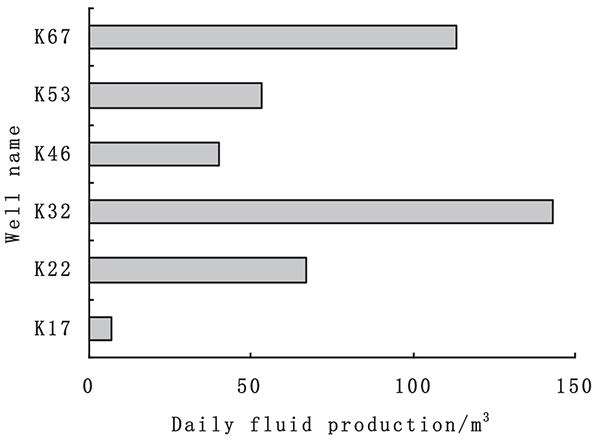 ). As one can see, production from wells K67 and K32 is higher than other wells by over 100 m3 per day. Wells K22, K53, and K46 produce 30-70 m3/day and production from the well K17 is poor. It can be concluded that the methodology developed and the zones delineated are consistent with the production data.
). As one can see, production from wells K67 and K32 is higher than other wells by over 100 m3 per day. Wells K22, K53, and K46 produce 30-70 m3/day and production from the well K17 is poor. It can be concluded that the methodology developed and the zones delineated are consistent with the production data.
Taking the carbonate reservoir of the Middle Ordovician in the Middle Tarim Basin as a case study, the complex carbonate reservoir is evaluated using the fuzzy logic analysis. The storage abundance, permeability, and median of pore throat radius are selected as the factors controlling reservoir characteristics. The carbonate reservoir is evaluated by constructing a membership function and determining weight of the fuzzy sets. The distribution of favorable reservoir is plotted by a single well evaluation result which reveals the distribution law of the reservoir. The results of fuzzy quantitative evaluation of the complex carbonate reservoir are consistent with the reservoir capacity. The classification of the reservoir into different zones in terms of reservoir quality can be used as the basis of optimal and effective reservoir development and management.
CONCLUSION
- A methodology based on fuzzy logic is developed and presented for quality assessment of complex and heterogeneous carbonate reservoirs. The developed method can be used to effectively integrate important reservoir parameters which reflect the uncertainties in the evaluation process and discrepancies in the reservoir assessment results.
- Based on the statistical analysis of the characteristics of the carbonate reservoirs in the study area, the storage abundance, permeability, and median pore throat radius are selected as the main factors. The distribution map of the favorable carbonate reservoir quality zones is prepared using single well evaluation results.
- By using fuzzy logic reservoir evaluation method, the Middle Ordovician Carbonate Reservoirs in the Middle Tarim Basin are classified into 3 categories. The carbonate reservoir evaluation results are consistent with the actual production data.
- The quality and accuracy of the contour maps of carbonate reservoir quality evaluation constructed by using fuzzy logic method can reflect the distribution of the favorable reservoir quality zones intuitively and accurately as long as the evaluation criteria are reasonable and the samples are reliable.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The author declares no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
The author gratefully acknowledges the editors and anonymous referees for their useful comments and suggestions which improved the quality of this manuscript.
REFERENCES
| [1] | W.F. Liu, "Fuzzy comprehensive evaluation of carbonate reservoir", J. Inf. Comput. Sci., vol. 12, no. 10, pp. 3819-3826, 2015. [http://dx.doi.org/10.12733/jics20106042] |
| [2] | Q.Y. Miao, X.M. Zhu, H.M. Guo, and H. Zhao, "Log evaluation of complex carbonate reservoirs in centre block of the eastern margin of Pre-caspian Basin", Well Logging Technol, vol. 38, no. 2, pp. 196-200, 2014. |
| [3] | B.K. Shen, D.W. Xue, J.Y. Zhao, and Y.D. Shen, "The logging evaluating method on carbonates reservoirs", Prog. Geophysiscs, vol. 39, no. 1, pp. 261-270, 2014. |
| [4] | T.J. Li, D.L. Guo, Y.J. Gong, and Z.H. Tang, "A research of fuzzy comprehensive evaluation on carbonate reservoir", Fuzzy Eng. Oper. Res., vol. 147, pp. 331-337, 2012. [http://dx.doi.org/10.1007/978-3-642-28592-9_34] |
| [5] | Z.Q. Gao, Z.B. Liu, and S.L. Gao, "Characteristics and genetic models of lower Ordovician carbonate reservoirs in Southwest Tarim Basin, NW China", J. Petrol. Sci. Eng., vol. 144, pp. 99-112, 2016. [http://dx.doi.org/10.1016/j.petrol.2016.03.007] |
| [6] | H. Pang, J.P. Chen, and X.Q. Pang, "Key factors controlling hydrocarbon accumulations in Ordovician carbonate reservoirs in the Tazhong area, Tarim basin, western China", Mar. Pet. Geol., vol. 43, pp. 88-101, 2013. [http://dx.doi.org/10.1016/j.marpetgeo.2013.03.002] |
| [7] | B. Li, and L. Xu, "Risk assessment of ground water inrush from underlying aquifers based on fuzzy comprehensive evaluation and its application", Open Fuels & Energy Sci. J, vol. 7, pp. 107-112, 2014. [http://dx.doi.org/10.2174/1876973X01407010107] |
| [8] | M.S. Mostafa, A.R. Hamid, and J. Hossein, "Selection of the best well control system by using fuzzy multiple-attribute decision-making methods", J. Appl. Stat., vol. 41, no. 5, pp. 1105-1121, 2014. [http://dx.doi.org/10.1080/02664763.2013.862218] |
| [9] | H.C. Liao, Z.S. Xu, X.J. Zeng, and D.L. Xu, "An enhanced consensus reaching process in group decision making with intuitionistic fuzzy preference relations", Inf. Sci., vol. 329, pp. 274-286, 2016. [http://dx.doi.org/10.1016/j.ins.2015.09.024] |
| [10] | M. Abdolreza, and T.M. Reza, "Cooperative spectrum sensing using fuzzy membership function of energy statistics", Int. J. Electron Commun., vol. 70, no. 3, pp. 234-240, 2016. [http://dx.doi.org/10.1016/j.aeue.2015.11.005] |
| [11] | B.L. Fang, "The fuzzy mathematical evaluation of new energy power generation performance", Open Fuels & Energy Sci. J., vol. 8, no. 1, pp. 238-243, 2015. [http://dx.doi.org/10.2174/1876973X01508010238] |
| [12] | A. Rami, M.D. Kudret, and K.G. Suresh, "Coping with uncertainties in production planning through fuzzy mathematical programming: application to steel rolling industry", Int. J. Oper. Res., vol. 22, no. 1, pp. 1-30, 2015. [http://dx.doi.org/10.1504/IJOR.2015.065937] |
| [13] | L. Xu, K. Zhu, and X.L. Yang, "Production forecasting of coalbed methane wells based on type-2 fuzzy logic system", Open Pet. Eng. J,, vol. 9, pp. 268-278, 2016. [http://dx.doi.org/10.2174/1874834101609010268] |
| [14] | J. Ghiasi, M. Ziaii, and A. Kadkhodaie, "A reservoir rock porosity estimation through image analysis and fuzzy logic techniques", Energy Sources, vol. 36, no. 6, pp. 1276-1284, 2014. [http://dx.doi.org/10.1080/15567036.2011.574198] |
| [15] | H. Dong, L.X. Wei, and Q.N. Wang, "A study on oil pipeline risk assessment technique based on fuzzy analytic hierarchy process", Open Pet. Eng. J., vol. 7, pp. 125-129, 2014. [http://dx.doi.org/10.2174/1874834101407010125] |







