- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Mathematics, Statistics and Probability Journal
The Open Statistics & Probability Journal
(Discontinued)
ISSN: 2666-1489 ― Volume 10, 2020
On Limited Length Binary Strings with an Application in Statistical Control
F.S. Makri1, *, Z.M. Psillakis2
Abstract
In a 0 - 1 sequence of Markov dependent trials we consider a statistic which counts strings of a limited length run of 0s between subsequent 1s. Its probability mass function is used to determine the chance that a stochastic process remains or not in statistical control. Illustrative numerics are presented.
Article Information
Identifiers and Pagination:
Year: 2017Volume: 8
First Page: 1
Last Page: 6
Publisher Id: TOSPJ-8-1
DOI: 10.2174/1876527001708010001
Article History:
Received Date: 04/08/2016Revision Received Date: 01/09/2016
Acceptance Date: 12/09/2016
Electronic publication date: 28/02/2017
Collection year: 2017
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
* Address correspondence to this author at the Department of Mathematics, University of Patras, 26500 Patras, Greece; Tel: 0030-2610-996738; E-mail: makri@math.upatras.gr
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 04-08-2016 |
Original Manuscript | On Limited Length Binary Strings with an Application in Statistical Control | |
1. INTRODUCTION AND PRELIMINARIES
Let {Xi}i≥1 be a sequence of binary random variables (RVs) with values 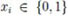 ordered on a line. For n ≥ 2 and two non-negative integer numbers k and l, 0 ≤ k ≤ l ≤ n – 2, we consider the statistic (random variable) Mn;k,l which enumerates strings (binary patterns)
ordered on a line. For n ≥ 2 and two non-negative integer numbers k and l, 0 ≤ k ≤ l ≤ n – 2, we consider the statistic (random variable) Mn;k,l which enumerates strings (binary patterns)
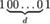 of a limited (constrained) length equal to d+2, k ≤ d ≤ l; i.e. strings which consist of a zero run (consecutive 0s) of length at least equal to k and at most equal to l between two subsequent ones. The counting of such constrained (k, l) strings is considered in the overlapping sense; that is, a 1 which is not at either end of the sequence may contribute towards counting two possible strings, the one which ends with the occurrence of it and the next one which starts with it.
of a limited (constrained) length equal to d+2, k ≤ d ≤ l; i.e. strings which consist of a zero run (consecutive 0s) of length at least equal to k and at most equal to l between two subsequent ones. The counting of such constrained (k, l) strings is considered in the overlapping sense; that is, a 1 which is not at either end of the sequence may contribute towards counting two possible strings, the one which ends with the occurrence of it and the next one which starts with it.
As an illustration let 0100010000111011001001100 be the first n = 25 outcomes of a 0 - 1 sequence. Then M25;1,2 = 3, M25;1,3 = 4, M25;0,0 = 4 and M25;0,4 = 9.
Let A = {k + 2, k + 3,..., n} be an index set and {B, Bc} a partition of A, where B = {k + 2, k + 3,..., l + 1} and Bc = {l + 2, l + 3,..., n}. Then formally, Mn;k,l, 0 ≤ k ≤ l ≤ n - 2, can be written, on a 0 - 1 sequence
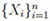 , as (see Makri and Psillakis [1F.S. Makri, and Z.M. Psillakis, "Exact distributions of constrained (k, l) strings of failures between subsequent successes", Stat. Papers, vol. 54, pp. 783-806, 2013.
, as (see Makri and Psillakis [1F.S. Makri, and Z.M. Psillakis, "Exact distributions of constrained (k, l) strings of failures between subsequent successes", Stat. Papers, vol. 54, pp. 783-806, 2013.
[http://dx.doi.org/10.1007/s00362-012-0462-1] ]):
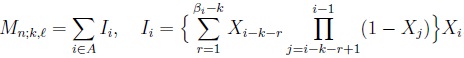 |
(1) |
with
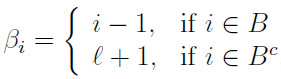 |
(2) |
Readily, for n < k + 2, Mn;k,l = 0. We notice that throughout the article we apply the conventions
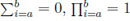 , for a > b; that is, an empty sum (product) is to be interpreted as a zero (unity). The support (range set) of Mn;k,l is:
, for a > b; that is, an empty sum (product) is to be interpreted as a zero (unity). The support (range set) of Mn;k,l is:
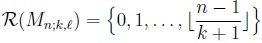 |
(3) |
where by
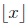 we denote the greatest integer less than or equal to a real number x.
we denote the greatest integer less than or equal to a real number x.
A statistic related to Mn;k,l is the waiting time Wm;k,l until the m-th, m ≥ 1, occurrence of a constrained (k, l) string. It is defined and connected to Mn;k,l as follows:
 |
(4) |
Hence, Eq. (4) offers an alternative way of obtaining results for the waiting time RV Wm;k,l through formulae established for the string enumerative RV Mn;k,l and vise versa.
The study, via Mn;k,l, of constrained (k, l) strings where a 1 is followed by at least k and at most l 0s before the next 1 in a 0 - 1 sequence covers as particular cases strings with zero run length at most equal (Mn;0,l, d ≤ l), exactly equal (Mn;k,k, d = k) and at least equal (Mn;k,n-2, d ≥ k) to a non-negative integer number. Some relevant contributions on the subject are the works of Sarkar et al. [2A. Sarkar, K. Sen, and Anuradha, "Waiting time distributions of runs in higher order Markov chains", Ann. Inst. Stat. Math., vol. 56, pp. 317-349, 2004.
[http://dx.doi.org/10.1007/BF02530548] ], Sen and Goyal [3K. Sen, and B. Goyal, "Distributions of patterns of two failures separated by success runs of length k", J. Korean Stat. Soc., vol. 33, pp. 35-58, 2004.], Holst [4L. Holst, "Counts of failure strings in certain Bernoulli sequences", J. Appl. Probab., vol. 44, pp. 824-830, 2007.
[http://dx.doi.org/10.1017/S0021900200003454] , 5L. Holst, "The number of two consecutive successes in a Hope-Polya urn", J. Appl. Probab., vol. 45, pp. 901-906, 2008.
[http://dx.doi.org/10.1017/S0021900200004770] ], Huffer et al. [6F.W. Huffer, J. Sethuraman, and S. Sethuraman, "A study of counts of Bernoulli strings via conditional Poisson processes", Proc. Am. Math. Soc., vol. 137, pp. 2125-2134, 2009.
[http://dx.doi.org/10.1090/S0002-9939-08-09793-1] ], Eryilmaz and Zuo [7S. Eryilmaz, and M. Zuo, "Constrained (k, d)-out-of-n systems", Int. J. Syst. Sci., vol. 41, pp. 679-685, 2010.
[http://dx.doi.org/10.1080/00207720903144537] ], Eryilmaz and Yalcin [8S. Eryilmaz, and F. Yalcin, "On the mean and extreme distances between failures in Markovian binary sequences", J. Comput. Appl. Math., vol. 236, pp. 1502-1510, 2011.
[http://dx.doi.org/10.1016/j.cam.2011.09.013] ], Dafnis et al. [9S.D. Dafnis, A.N. Philippou, and D.L. Antzoulakos, "Distributions of patterns of two successes separated by a string of k-2 failures", Stat. Papers, vol. 53, pp. 323-344, 2012.
[http://dx.doi.org/10.1007/s00362-010-0340-7] ], and Makri and Psillakis [10F.S. Makri, and Z.M. Psillakis, "Counting certain binary strings", J. Stat. Plan. Inference, vol. 142, pp. 908-924, 2012.
[http://dx.doi.org/10.1016/j.jspi.2011.10.015] ]. Moreover, Mn;0,0 is the Ling’s [11K.D. Ling, "On binomial distributions of order k", Stat. Probab. Lett., vol. 6, pp. 247-250, 1988.
[http://dx.doi.org/10.1016/0167-7152(88)90069-7] ] RV
 which counts overlapping runs of 1s of length 2 (with overlapping part of length at most 1), see e.g. Balakrishnan and Koutras [12N. Balakrishnan, and M.V. Koutras, Runs and scans with applications., Wiley: New York, 2002.].
which counts overlapping runs of 1s of length 2 (with overlapping part of length at most 1), see e.g. Balakrishnan and Koutras [12N. Balakrishnan, and M.V. Koutras, Runs and scans with applications., Wiley: New York, 2002.].
In Section 2 of the present paper we first introduce the required notation and second we recall a recent result of Makri and Psillakis [1F.S. Makri, and Z.M. Psillakis, "Exact distributions of constrained (k, l) strings of failures between subsequent successes", Stat. Papers, vol. 54, pp. 783-806, 2013.
[http://dx.doi.org/10.1007/s00362-012-0462-1] ] which refers to the probability mass function (PMF) of Mn;k,l defined on a 0 - 1 Markov chain. The presented expressions for the PMF are then used in an application case study which is discussed in Section 3 and it refers to statistical process control.
Throughout the article, δi,j denotes the Kronecker delta function of the integer arguments i and j.
2. PMF OF Mn;k,l FOR MARKOV DEPENDENT TRIALS
In this Section we provide the PMF fn;k,l(x) = P(Mn;k,l = x),
 , 0 ≤ k ≤ l ≤ n - 2. The 0 - 1 sequence
, 0 ≤ k ≤ l ≤ n - 2. The 0 - 1 sequence
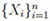 , n ≥ 2 on which Mn;k,l is defined, is generated by a time-homogeneous first order Markov chain (MRKV) with one step transition probability matrix P = (pi,j) and initial probability vector p(1) =
, n ≥ 2 on which Mn;k,l is defined, is generated by a time-homogeneous first order Markov chain (MRKV) with one step transition probability matrix P = (pi,j) and initial probability vector p(1) = 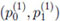 with
with
 , t ≥ 2,
, t ≥ 2,
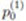 = P(X1 = 0) = 1 - P(X1 = 1) = 1 -
= P(X1 = 0) = 1 - P(X1 = 1) = 1 - 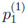 and
and
 . Readily, a 0 - 1 sequence
. Readily, a 0 - 1 sequence
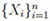 , n ≥ 2 of independent and identically distributed (IID) RVs with a common probability of 1s, p = P(Xi = 1) = 1 - P(Xi = 0) = 1 - q, i = 1,2,...,n is a particular MRKV sequence with p00 = p10 = q, p01 = p11 = p and
, n ≥ 2 of independent and identically distributed (IID) RVs with a common probability of 1s, p = P(Xi = 1) = 1 - P(Xi = 0) = 1 - q, i = 1,2,...,n is a particular MRKV sequence with p00 = p10 = q, p01 = p11 = p and 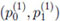 = (q, p).
= (q, p).
We next present two combinatorial results (Lemma 1 and Corollary 1) which then are used for the calculation of fn;k,l(x) given by Proposition 1.
Lemma 1 (Makri et al. [13F.S. Makri, A.N. Philippou, and Z.M. Psillakis, "Polya, inverse Polya, and circular Polya distributions of order k for l-overlapping success runs", Commun. Stat. Theory Methods, vol. 36, pp. 657-668, 2007.
[http://dx.doi.org/10.1080/03610920601033942] ]) Let Ci,r-i(α, m, k1 - 1, k2 - 1) be the number of allocations of α indistinguishable balls into m distinguishable cells, i specified of which have capacity k1 - 1 and each of r-i specified cells has capacity k2 - 1, 0 ≤ r ≤ m, 0 ≤ i ≤ r, k1 ≥ 1, k2 ≥ 1 . Then,
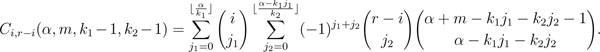 |
(5) |
We note that the number Ci,r-i(α, m, k1 - 1, k2 - 1) equivalently gives the number of integer solutions of the equation x1 + x2 +...+ xm = α such that 0 ≤ xj < k1, 1 ≤ j ≤ i and 0 ≤ xi+j < k2, 1 ≤ j ≤ r-i. Setting k1 = k2 = k in Lemma 1 we obtain, as a corollary, the following result.
Corollary 1 (Makri et al. [14F.S. Makri, A.N. Philippou, and Z.M. Psillakis, "Success run statistics defined on an urn model", Adv. Appl. Probab., vol. 39, pp. 991-1019, 2007.
[http://dx.doi.org/10.1017/S0001867800002202] ]). Let Hr(α, m, k - 1) be the number of allocations of α indistinguishable balls into m distinguishable cells where each of the r, 0 ≤ r ≤ m, specified cells is occupied by at most k - 1 balls. Then, Hr(α, m, k - 1) = Ci,r-i(α, m, k - 1, k - 1). Accordingly,
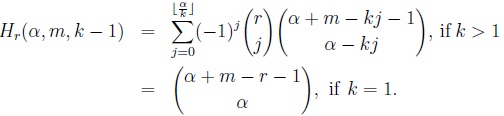 |
(6) |
Proposition 1 (Makri and Psillakis [1F.S. Makri, and Z.M. Psillakis, "Exact distributions of constrained (k, l) strings of failures between subsequent successes", Stat. Papers, vol. 54, pp. 783-806, 2013.
[http://dx.doi.org/10.1007/s00362-012-0462-1] ]). For p(1) =
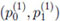 = (p0 , p1) and
= (p0 , p1) and
 the PMF fn;k,l(x),
the PMF fn;k,l(x),
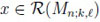 , n ≥ k + 2 is given by:
, n ≥ k + 2 is given by:
 |
(7) |
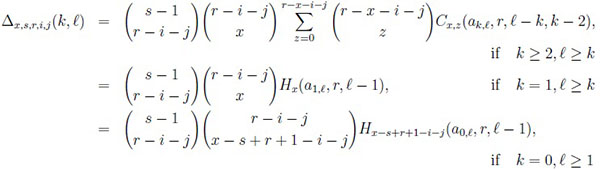 |
with
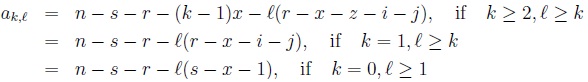 |
and
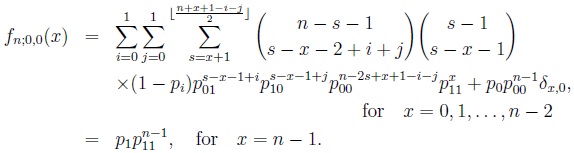 |
(8) |
3. A NOTE FOR APPLICATION: STATISTICAL PROCESS CONTROL
Suppose we observe values of a stochastic process {Yi}i≥1 which operates under chance causes in or out an acceptable zone of interest (ZI); i.e. the process is in statistical control. We are interested in remaining the process in ZI, otherwise a risky or an awkward situation of the process might appear. For instance, a ZI might be a control zone in a statistical control chart, a trading zone in a stock or exchange market, a comfort zone in a patient mechanical support system, a zone of acceptable items with specific characteristics in an assembly line, etc.
We denote by 0 and 1 the occurrence of the value of the process in and out of ZI, respectively. We assume that each value of the process is out of ZI with probability p01 or p11 if the previous value was in or out of ZI, respectively. Therefore, the indicator RVs Xi = 0, if  ; 1, otherwise constitute a 0 - 1 Markov chain {Xi}i≥1 with transition probability matrix
; 1, otherwise constitute a 0 - 1 Markov chain {Xi}i≥1 with transition probability matrix
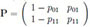 and initial probability vector p(1) = (1 - p1, p1). In practise, ZI and p01, p11 might be evaluated from a reference sample in Phase I (retrospective) analysis of the process whereas the monitoring of the process, we are interested in, is considered as Phase II (prospective) analysis of the process (see, e.g. Chakraborti et al. [15S. Chakraborti, S. Eryilmaz, and S.W. Human, "A phase II nonparametric control chart based on precedence statistics with runs-type signaling rules", Comput. Stat. Data Anal., vol. 53, pp. 1054-1065, 2009.
and initial probability vector p(1) = (1 - p1, p1). In practise, ZI and p01, p11 might be evaluated from a reference sample in Phase I (retrospective) analysis of the process whereas the monitoring of the process, we are interested in, is considered as Phase II (prospective) analysis of the process (see, e.g. Chakraborti et al. [15S. Chakraborti, S. Eryilmaz, and S.W. Human, "A phase II nonparametric control chart based on precedence statistics with runs-type signaling rules", Comput. Stat. Data Anal., vol. 53, pp. 1054-1065, 2009.
[http://dx.doi.org/10.1016/j.csda.2008.09.025] ]).
Following Dafnis and Philippou [16S.D. Dafnis, and A.N. Philippou, "Distributions of patterns with applications in engineering", IAENG Int. J. Appl. Math., vol. 41, pp. 68-75, 2011.] we interpret the occurrence of two subsequent 1s separated by at least k and at most l 0s as a sign that the process leaves its ZI and it enters in a risky situation for which additional care has to be paid. In such a case the number of values in ZI is not enough to compensate for the others out of it. What values of k and l should depend on the under study process.
Accordingly, the event of having m (≥1) or more constrained (k, l) strings in a stream of n future values of the process could serve as an index that the process will not any more be bounded in its ZI. The risk of experiencing of such an event would be measured by P(Mn;k,l≥m) = P(Wm;k,l≤n). Therefore, the distributions and the characteristics of the related RVs Mn;k,l and Wm;k,l would be of importance in understanding the future process behavior. Usually in practice, we consider a detector that counts such events and consequently sends an alarm signal to a process monitoring system. The detector’s tolerance (the false alarm probability) is taken to be at most equal to γ (0 < γ < 1) so that an expected number, γ100%, of false alarms happen. For a given γ a critical value of m (if there is such a value for the selected γ and the process parameters n, k, l and p1, p01, p11) mγ is: mγ = min{m ≥ 1: P(Mn;k,l≥m) = γ* ≤ γ}. The probability γ* is the largest real number which does not exceed γ. It may not be equal (in fact it is rare to be equal) to the assigned probability γ, as it refers to the discrete RV Mn;k,l.
As a numerical example we consider Markov dependent trials with p1 = 0.5, p01 = 0.45 and p11 = 0.90. That is, we assume that the process has 50-50 chance to be initially in or out its ZI and the occurrence of a value out of ZI implies that the process continues to remain out of ZI with large probability, in fact twice the probability that the process leaves its ZI. The latter one is assumed to be a little smaller than 0.5.
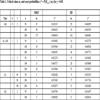
For a reasonable value of the detector’s tolerance γ = 0.05 and for large enough values of n, we present in Table 1 critical values mγ, and exact probabilities γ* = P(Mn;k,l≥mγ) for several constrained (k, l) strings of type at most (AM), at least (AL), at least - at most (AL-AM) and equal (EQ). For comparison we have included in the Table the respective mγ and γ* for IID trials with p = 0.5.
The entries of Table 1 suggest that in order to have at most 5 false alarms in a total of 100 alarms in a stream of n future values of a process, defined on MRKV with the prementioned values p01, p11 and p1, we have to take larger mγ when we use a (0, 2) string than mγ of a (2, 2) string. This is so, because a (2, 2) string is one of the strings counted as a (0, 2) string and therefore as a more strict pattern is a less frequently appearing string, as a warning pattern, than a (0, 2) string. Analogous arguments/interpretations are also suggested for the other presented types of strings as well as when someone compares MRKV and IID trials.
CONCLUSION
In this study the RV Mn;k;l counting a flexible class of binary strings of a limited length is considered. A potential application of its PMF in describing the probabilistic behavior of a binary stochastic process is discussed. The stochastic process is assumed to operate under chance in or out an acceptable zone of interest. Such a zone can be a control chart zone, a trading zone of a stock market, etc. An index connected to the number of occurrences of limited length binary strings is properly defined via the PMF of Mn;k;l. Accordingly, it is then used to determine whether or not the process is or not under statistical control. Numerical results clarify the implementation of several types of binary strings used in the control process.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
The authors wish to thank the anonymous referee for the through reading and suggestions which helped to improve the paper.
REFERENCES
| [1] | F.S. Makri, and Z.M. Psillakis, "Exact distributions of constrained (k, l) strings of failures between subsequent successes", Stat. Papers, vol. 54, pp. 783-806, 2013. [http://dx.doi.org/10.1007/s00362-012-0462-1] |
| [2] | A. Sarkar, K. Sen, and Anuradha, "Waiting time distributions of runs in higher order Markov chains", Ann. Inst. Stat. Math., vol. 56, pp. 317-349, 2004. [http://dx.doi.org/10.1007/BF02530548] |
| [3] | K. Sen, and B. Goyal, "Distributions of patterns of two failures separated by success runs of length k", J. Korean Stat. Soc., vol. 33, pp. 35-58, 2004. |
| [4] | L. Holst, "Counts of failure strings in certain Bernoulli sequences", J. Appl. Probab., vol. 44, pp. 824-830, 2007. [http://dx.doi.org/10.1017/S0021900200003454] |
| [5] | L. Holst, "The number of two consecutive successes in a Hope-Polya urn", J. Appl. Probab., vol. 45, pp. 901-906, 2008. [http://dx.doi.org/10.1017/S0021900200004770] |
| [6] | F.W. Huffer, J. Sethuraman, and S. Sethuraman, "A study of counts of Bernoulli strings via conditional Poisson processes", Proc. Am. Math. Soc., vol. 137, pp. 2125-2134, 2009. [http://dx.doi.org/10.1090/S0002-9939-08-09793-1] |
| [7] | S. Eryilmaz, and M. Zuo, "Constrained (k, d)-out-of-n systems", Int. J. Syst. Sci., vol. 41, pp. 679-685, 2010. [http://dx.doi.org/10.1080/00207720903144537] |
| [8] | S. Eryilmaz, and F. Yalcin, "On the mean and extreme distances between failures in Markovian binary sequences", J. Comput. Appl. Math., vol. 236, pp. 1502-1510, 2011. [http://dx.doi.org/10.1016/j.cam.2011.09.013] |
| [9] | S.D. Dafnis, A.N. Philippou, and D.L. Antzoulakos, "Distributions of patterns of two successes separated by a string of k-2 failures", Stat. Papers, vol. 53, pp. 323-344, 2012. [http://dx.doi.org/10.1007/s00362-010-0340-7] |
| [10] | F.S. Makri, and Z.M. Psillakis, "Counting certain binary strings", J. Stat. Plan. Inference, vol. 142, pp. 908-924, 2012. [http://dx.doi.org/10.1016/j.jspi.2011.10.015] |
| [11] | K.D. Ling, "On binomial distributions of order k", Stat. Probab. Lett., vol. 6, pp. 247-250, 1988. [http://dx.doi.org/10.1016/0167-7152(88)90069-7] |
| [12] | N. Balakrishnan, and M.V. Koutras, Runs and scans with applications., Wiley: New York, 2002. |
| [13] | F.S. Makri, A.N. Philippou, and Z.M. Psillakis, "Polya, inverse Polya, and circular Polya distributions of order k for l-overlapping success runs", Commun. Stat. Theory Methods, vol. 36, pp. 657-668, 2007. [http://dx.doi.org/10.1080/03610920601033942] |
| [14] | F.S. Makri, A.N. Philippou, and Z.M. Psillakis, "Success run statistics defined on an urn model", Adv. Appl. Probab., vol. 39, pp. 991-1019, 2007. [http://dx.doi.org/10.1017/S0001867800002202] |
| [15] | S. Chakraborti, S. Eryilmaz, and S.W. Human, "A phase II nonparametric control chart based on precedence statistics with runs-type signaling rules", Comput. Stat. Data Anal., vol. 53, pp. 1054-1065, 2009. [http://dx.doi.org/10.1016/j.csda.2008.09.025] |
| [16] | S.D. Dafnis, and A.N. Philippou, "Distributions of patterns with applications in engineering", IAENG Int. J. Appl. Math., vol. 41, pp. 68-75, 2011. |