- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Mathematics, Statistics and Probability Journal
The Open Statistics & Probability Journal
(Discontinued)
ISSN: 2666-1489 ― Volume 10, 2020
Clustering Directions Based on the Estimation of a Mixture of Von Mises-Fisher Distributions
Adelaide Figueiredo*
Abstract
Background:
In the statistical analysis of directional data, the von Mises-Fisher distribution plays an important role to model unit vectors. The estimation of the parameters of a mixture of von Mises-Fisher distributions can be done through the Estimation-Maximization algorithm.
Objective:
In this paper we propose a dynamic clusters type algorithm based on the estimation of the parameters of a mixture of von Mises-Fisher distributions for clustering directions, and we compare this algorithm with the Estimation-Maximization algorithm. We also define the between-groups and within-groups variability measures to compare the solutions obtained with the algorithms through these measures.
Results:
The comparison of the clusters obtained with both algorithms is provided for a simulation study based on samples generated from a mixture of two Fisher distributions and for an illustrative example with spherical data.
Article Information
Identifiers and Pagination:
Year: 2017Volume: 08
First Page: 39
Last Page: 52
Publisher Id: TOSPJ-8-39
DOI: 10.2174/1876527001708010039
Article History:
Received Date: 11/09/2017Revision Received Date: 28/11/2017
Acceptance Date: 29/11/2017
Electronic publication date: 29/12/2017
Collection year: 2017
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
* Address correspondence to this author at the University of Porto, Faculty of Economics, Porto and LIAAD-INESC TEC, Portugal,
Tel: (+351)220426449; E-mail: Adelaide@fep.up.pt
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 11-09-2017 |
Original Manuscript | Clustering Directions Based on the Estimation of a Mixture of Von Mises-Fisher Distributions | |
1. INTRODUCTION
Clustering data in the unit sphere is an important task in modern data analysis, for example, in clustering text documents when analysing textual data.
One approach to address such issue is the spherical k-means clustering. This technique was proposed by Dhillon and Modha (2001) [1I.S. Dhillon, and D.S. Modha, "Concept Decompositions for large Sparse Text Data Using Clustering", Mach. Learn., vol. 42, no. 1, pp. 143-175.
[http://dx.doi.org/10.1023/A:1007612920971] ] and implemented in a R package, called skmeans by Hornik et al. (2012) [2K. Hornik, I. Feinerer, M. Kober, and C. Buchta, "Spherical k-Means Clustering", J. Stat. Softw., vol. 50, no. 10, pp. 1-21.
[http://dx.doi.org/10.18637/jss.v050.i10] [PMID: 25317082] ], and it is based on the cosine similarity to obtain a partition of term weight representation of the documents.
Other works that have appeared in the literature for clustering directional data are based on model-based clustering methods. For instance, Peel et al. (2001) [3D. Peel, W.J. Whiten, and G.J. McLachlan, "Fitting mixtures of Kent distributions to aid in joint set identification", J. Am. Stat. Assoc., vol. 96, no. 453, pp. 56-63.
[http://dx.doi.org/10.1198/016214501750332974] ] used the Kent distribution [4J.T. Kent, "The Fisher-Bingham distribution on the sphere", J. R. Stat. Soc. B, vol. 44, no. 1, pp. 71-80.] to form groups of fracture data through a model-based clustering and Dortet-Bernadet and Wicker (2008) [5J-L. Dortet-Bernadet, and N. Wicker, "Model-based clustering on the unit sphere with an illustration using gene expression profiles", Biostatistics, vol. 9, no. 1, pp. 66-80.
[http://dx.doi.org/10.1093/biostatistics/kxm012] [PMID: 17468207] ] supposed a model-based clustering of data that lies on a unit sphere and applied this clustering method to gene expression profiles. Banerjee et al. (2005) [6A. Banerjee, I.S. Dhillon, J. Ghosh, and S. Sra, "Clustering on the unit hypersphere using von Mises-Fisher distributions", J. Mach. Learn. Res., vol. 6, pp. 1345-1382.] applied a model-based clustering of directional data to text analysis. These authors considered the estimation of a mixture of von Mises-Fisher distributions using two variants of the Estimation-Maximization EM algorithm, denoted by soft-movMF and hard-movMF algorithms. Another variant of the EM algorithm, denoted by stochastic EM was given by Celeux and Govaert (1992) [7G. Celeux, and G. Govaert, "A classification EM algorithm for clustering and two-stochastic versions", Comput. Stat. Data Anal., vol. 14, no. 3, pp. 315-332.
[http://dx.doi.org/10.1016/0167-9473(92)90042-E] ]. Banerjee et al. (2005) [6A. Banerjee, I.S. Dhillon, J. Ghosh, and S. Sra, "Clustering on the unit hypersphere using von Mises-Fisher distributions", J. Mach. Learn. Res., vol. 6, pp. 1345-1382.] showed that the spherical k-means algorithm may be obtained as a variant of the EM algorithm for the maximum likelihood estimation of the mean direction parameters of a mixture of von Mises-Fisher distributions with common concentration parameter κ, using hard-max classification E-step. Figueiredo and Gomes (2015) [8A. Figueiredo, and P. Gomes, "Clustering of variables based on Watson distribution on hypersphere: A comparison of algorithms", Communications in Statistics -Simulation and Computation., vol. 44, no. 10, pp. 2622-2635.Special issue: Joint Meeting of y-BIS and jSPE, 2015.] proposed an algorithm based on the dynamic clusters algorithm proposed by Diday and Schroeder (1976) [9E. Diday, and A. Schroeder, "New approach in mixed distributions detection, Révue Française D’Automátique", Automatique Informatique Recherche Operationelle, vol. 10, no. 6, pp. 75-106.
[http://dx.doi.org/10.1051/ro/197610V200751] ] for the estimation of the parameters of a mixture of Watson distributions defined on the hypersphere and compared it with the EM algorithm, proposed by Dempster et al. (1977) [10A.P. Dempster, N.M. Laird, and D.B. Rubin, "Maximum likelihood from incomplete data via the EM algorithm (with discussion)", J. R. Stat. Soc. B, vol. 3, no. 1, pp. 1-38.] for problems of incomplete data. Similarly in this paper, to estimate the parameters of a mixture of k von Mises-Fisher distributions and obtain a partition of the sample into clusters, we propose a dynamic clusters type algorithm and we compare it with the EM algorithm. This proposed algorithm has the advantage of converging quickly to a local optimum, while the EM algorithm may converge slowly to the local optimum. On the other hand, the EM algorithm provides strongly consistent estimators with asymptotic normal distribution (Redner and Walker, 1984) [11R. Redner, and W. Homer, "Mixture Densities, Maximum Likelihood, EM algorithm", J. R. Stat. Soc. B, vol. 39, no. 2, pp. 1-38.]. For comparing the solutions obtained in both algorithms, we define between-groups and within-groups variability measures. Then, for several generated samples and a real data set we compare the solutions obtained with these algorithms.
In Section 2, we recall the von Mises-Fisher distribution and the maximum likelihood estimators of the parameters of this distribution. In Section 3, we describe the EM algorithm and we propose the dynamic clusters type algorithm for the estimation of a mixture of k von Mises-Fisher distributions. In Section 4, we define the variability measures and we compare the algorithms through these measures, using simulated data from von Mises-Fisher populations and a real data set. In Section 5 we present some concluding remarks.
2. VON MISES-FISHER DISTRIBUTION
The von Mises-Fisher distribution is one of the most used distributions in the statistical analysis of directional data. It is usually denoted by Mp (µ, κ) and has probability density function defined by
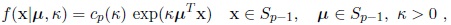 |
(1) |
where the normalising constant is given by
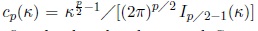 , and Iv (.) denotes the modified Bessel function of the first kind and order ν and Sp−1 denotes the unit sphere in
, and Iv (.) denotes the modified Bessel function of the first kind and order ν and Sp−1 denotes the unit sphere in
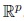 . This distribution is called von Mises distribution for circular data and Fisher distribution for spherical data. The parameter µ is the vector of the mean direction and κ is the concentration parameter around µ. This distribution is rotationally symmetric about µ.
. This distribution is called von Mises distribution for circular data and Fisher distribution for spherical data. The parameter µ is the vector of the mean direction and κ is the concentration parameter around µ. This distribution is rotationally symmetric about µ.
Let (x1, x2, ...,xn) be a random sample of size n from the von Mises-Fisher distribution, Mp (µ, κ) . Let
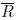 be the resultant length mean of the sample defined
be the resultant length mean of the sample defined
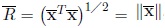 where
where
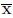 is the sample mean vector of (x1, x2, ...,xn) defined by
is the sample mean vector of (x1, x2, ...,xn) defined by
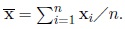 . The maximum likelihood estimator of µ is the sample mean direction, i.e.,
. The maximum likelihood estimator of µ is the sample mean direction, i.e.,
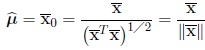 |
and the maximum likelihood estimator of κ is the solution of the equation
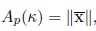 |
where the function Ap (κ) is defined by
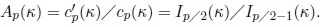 .
.
For more details about this distribution, see for instance, Mardia and Jupp (2000), p. 198. [12K.V. Mardia, and P.E. Jupp, Directional Statistics., John Wiley and Sons: Chichester, .]
3. ESTIMATION OF A MIXTURE OF K VON MISES-FISHER DISTRIBUTIONS
A mixture of k von Mises-Fisher components C1,...,Ck has probability density function given by
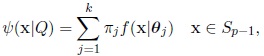 |
(2) |
where
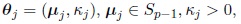 and
and
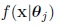 is the density function of the Cj component, i.e., the density of Mp (µj, κj) distribution. The parameters πj, j = 1, .., k with 0 < πj < 1 and
is the density function of the Cj component, i.e., the density of Mp (µj, κj) distribution. The parameters πj, j = 1, .., k with 0 < πj < 1 and
 are the proportions of the mixture, Q = (V, θ), with V = (π1,π2,.....πk) and θ = (θ1,....,θk) is the vector of unknown parameters of the mixture.
are the proportions of the mixture, Q = (V, θ), with V = (π1,π2,.....πk) and θ = (θ1,....,θk) is the vector of unknown parameters of the mixture.
For the estimation of the parameters of the mixture, we review the EM algorithm and its variants (soft-movMF, hard-movMF and stochastic EM) in Subsection 3.1. and we propose a dynamic clusters type algorithm in Subsection 3.2.
3.1. EM Algorithm
The Estimation-Maximization (EM) algorithm is used to obtain the maximum likelihood estimates of the parameters of the mixture and can be briefly described as follows.
Let (x1, x2, ...,xn) be a random sample from the mixture and let Z = (z1, z2, ....,zn) be the be the missing data, where the indicator vector zi =
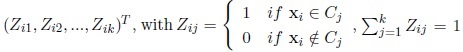 indicates the component of the mixture for xi. The expected log-likelihood as associated with the complete sample (x1, ....,xn, Z), derived in Appendix A, is given by
indicates the component of the mixture for xi. The expected log-likelihood as associated with the complete sample (x1, ....,xn, Z), derived in Appendix A, is given by
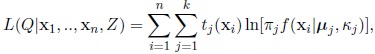 |
(3) |
where tj(xi) is the a-posteriori probability of xi belonging to Cj defined by
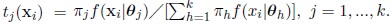
So (3) may be written as
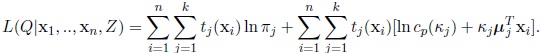 |
(4) |
Let
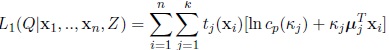 |
(5) |
and let
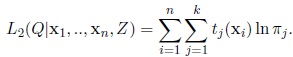 |
(6) |
To estimate the vector of unknown parameters Q, the EM algorithm uses iteratively the two steps: Estimation (E) and Maximization (M).
The algorithm starts with an initial solution:
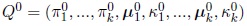 or with an initial partition into k groups, and then determine the estimates Q 0 based on the partition. In the mth iteration (m ≥ 1) the steps are:
or with an initial partition into k groups, and then determine the estimates Q 0 based on the partition. In the mth iteration (m ≥ 1) the steps are:
E -Step
For j = 1,...,k, i = 1,...,n, calculate the a-posteriori probability of xi belonging to the j th component of the mixture
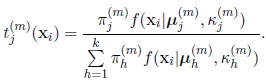 |
(7) |
M -Step
Use estimates tj(m) (xi) to maximize L1 (Q|x1, ...,xn, Z) subject to the constraint µTj µj = 1 and L2 (Q|x1, ..,xn, Z) subject to the constraint
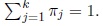 The estimators obtained, derived in Appendix B, are the following:
The estimators obtained, derived in Appendix B, are the following:
• The maximum likelihood estimator of µj in the (m + 1)th iteration,
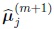 is given by
is given by
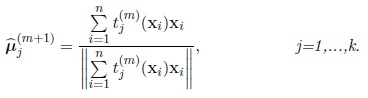 |
(8) |
• The maximum likelihood estimator of kj in the (m + 1)th iteration,
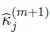 is the solution of the equation
is the solution of the equation
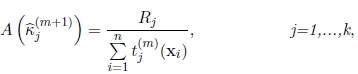 |
(9) |
where Rj is the length of the vector
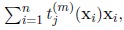 , that is
, that is
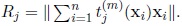 .
.
• The maximum likelihood estimator of πj in the (m + 1)th iteration,
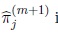 is given by
is given by
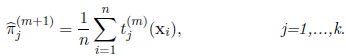 |
(10) |
In the particular case of components with the same concentration parameter k, the estimates of µj and πj , j = 1, ..., k, are given by the expressions (8) and (10), and the estimate of the common concentration parameter κ, derived in Appendix C, is the solution of the equation
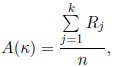 |
(11) |
where Rj is defined as before.
The EM algorithm is assumed to have converged if the relative change in the log-likelihood values is smaller than a threshold or if the relative absolute change in the parameters is smaller than a threshold. A partition (P1, ..., Pk ) of the sample is obtained assigning xi to the component for which the aposteriori probability is the largest, that is,
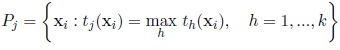 |
(12) |
and when tj (xi) = th (xi) consider
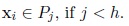
This algorithm is denoted by soft-movMF algorithm by Banerjee et al. (2005, p. 1357) [6A. Banerjee, I.S. Dhillon, J. Ghosh, and S. Sra, "Clustering on the unit hypersphere using von Mises-Fisher distributions", J. Mach. Learn. Res., vol. 6, pp. 1345-1382.]. These authors also proposed the hard-movMF algorithm (p. 1358), which is a modification of the soft-movMF by adding a hardening step (H -step) between E -step and M -step. This step is:
H -Step
Replace the aposteriori probabilities by assigning each observation with probability 1 to the component for which its aposteriori probability is maximum.
Celeux and Govaert (1992) [7G. Celeux, and G. Govaert, "A classification EM algorithm for clustering and two-stochastic versions", Comput. Stat. Data Anal., vol. 14, no. 3, pp. 315-332.
[http://dx.doi.org/10.1016/0167-9473(92)90042-E] ] denoted the previous algorithm by Classification EM algorithm and proposed another variant of the EM algorithm, the stochastic EM, where instead of the hardening step, a stochastic step (S -step) is added between E -step and M -step. This step is:
S -Step
Assign at random each observation to one component with probability equal to its aposteriori probability.
These three variants of the EM algorithm are implemented in a R package called movMF [13K. Hornik, and B. Grun, "movMF: An R Package for fitting mixtures of von Mises-Fisher distributions", J. Stat. Softw., vol. 58, no. 10, pp. 1-26.
[http://dx.doi.org/10.18637/jss.v058.i10] ].
3.2. Dynamic Clusters Type Algorithm
Let E be a finite sample. The aim is to determine a partition P = (P1, P2, ..., Pk) of E into k classes, so that for every j (1 ≤ j ≤ k), Pj may be considered as a sample from a population with density fθ .
Let 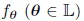 be the family of probability densities, from which the distributions of the different components belong: θ is a vectorial parameter and L its definition space:
be the family of probability densities, from which the distributions of the different components belong: θ is a vectorial parameter and L its definition space:
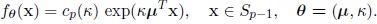 |
(13) |
Let Pk be the set of partitions of E into k classes and let
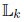 be the set of vectors of dimension k of L. The method starts with an initial partition
be the set of vectors of dimension k of L. The method starts with an initial partition
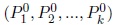 of E or starts with a vector of dimension k of values of the unknown parameter vector of dimension k of values of the unknown parameter
of E or starts with a vector of dimension k of values of the unknown parameter vector of dimension k of values of the unknown parameter
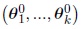 .
.
The two following functions f and g are successively applied until obtaining stable elements of L and P:
f: Lk → Pk
L → P
where L = (θ1, ...,θk ) and P = (P1, ..., Pk), so that for
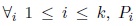 is the set of observations, which are less distant from the distribution fθi than from others. Then, it is important to define a function D, which measures the distance from an observation
is the set of observations, which are less distant from the distribution fθi than from others. Then, it is important to define a function D, which measures the distance from an observation
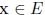 to a distribution fθ :
to a distribution fθ :
D: E × L → R+
(x, θ) → D (x, θ) .
The distance is defined by
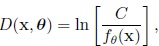 |
(14) |
where C is a constant defined by
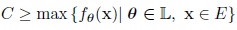 Then
Then
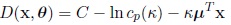 |
(15) |
and each group Pi is defined by
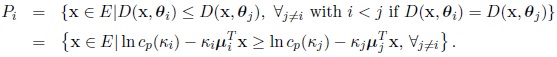 |
The function
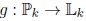
P → L
is such that for
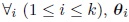 satisfies the condition
satisfies the condition
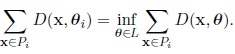 |
(16) |
The optimum value of θi is the maximum likelihood estimator of θi associated with Pi and the optimum criterion is function of the partition P * and L*
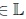 obtained in convergence:
obtained in convergence:
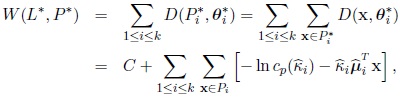 |
where C is the constant previously defined and
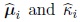 are the maximum likelihood estimators of µi and κi respectively, based on the sample Pi. Then,
are the maximum likelihood estimators of µi and κi respectively, based on the sample Pi. Then,
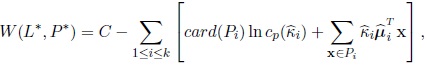 |
(17) |
where card (Pi) is the number of observations of Pi. So the parameters θI are estimated based on the k classes Pi: the function g defines the estimation by the maximum likelihood method and the function f enables us to define again k new classes Pi and then, evaluate again the value of the criterion W.
4. COMPARISON OF THE ALGORITHMS
For comparing the solutions obtained with the algorithms, we define next the between-groups and within-groups variability measures, in the decomposition of the total variability used to test the null hypothesis of a common mean vector across k von Mises-Fisher populations with concentration parameters not necessarily equal. This test was considered in the literature for the particular case of equal concentration parameters, for the circle or the sphere, see for instance, Mardia and Jupp (2000, pp. 222-226) [12K.V. Mardia, and P.E. Jupp, Directional Statistics., John Wiley and Sons: Chichester, .], Watson (1956) [14G.S. Watson, "Analysis of dispersion on a sphere", Monthly Notices of the Royal Astronomical Society Geophysical, vol. 7, no. 4, pp. 153-159.
[http://dx.doi.org/10.1111/j.1365-246X.1956.tb05560.x] ], Watson and Williams (1956) [15G.S. Watson, and E.J. Williams, "On the construction of significance tests on the circle and the sphere", Biometrika, vol. 43, no. 3-4, pp. 344-352.
[http://dx.doi.org/10.1093/biomet/43.3-4.344] ] and Harrison et al. (1986) [16D. Harrison, G.K. Kanji, and R.J. Gadsden, "Analysis of variance for circular data", J. Appl. Stat., vol. 13, no. 2, pp. 123-138.
[http://dx.doi.org/10.1080/02664768600000021] ].
Let xi1, ...,xini (i = 1, ..., k) be k independent random samples of sizes n1, ..., nk from populations Mp (µi, κi) , with vectors of the mean direction µi and concentration parameters κi, i = 1, ..., k. Let n = n1 + ... + nk be the global sample size. The null hypothesis of interest is
H 0: µ1 = .... = µk = µ,
against the alternative hypothesis that at least one of the equalities is not satisfied.
Next we consider the concentration parameters κi unknown, but if these parameters are unknown, we have to estimate them through their maximum likelihood estimates for instance. Let’s consider the following identity
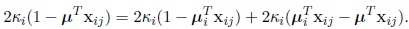 |
Summing from i = 1 to k, j = 1 to ni and replacing µ and µi by their maximum likelihood estimates, the following identity is obtained
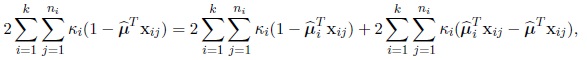 |
(18) |
where
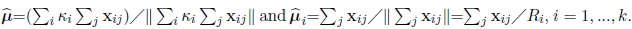
The previous identity can be written as
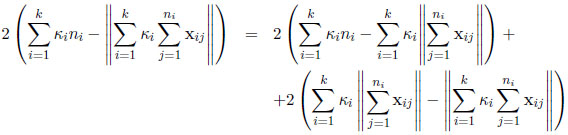 |
or equivalently,
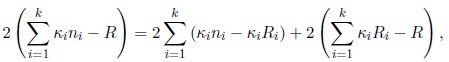 |
(19) |
where
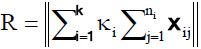 and Ri is the resultant length of the ith sample. This identity is the decomposition of total variability
and Ri is the resultant length of the ith sample. This identity is the decomposition of total variability
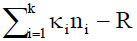 into within-groups variability
into within-groups variability
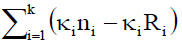 and between-groups variability
and between-groups variability
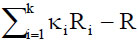 The test statistic is defined by
The test statistic is defined by
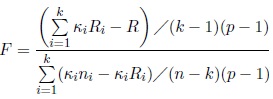 |
(20) |
and the hypothesis H 0 is rejected for large values of F . When all concentration parameters κi are equal to κ, the statistic (20) reduces to the following statistic given in Mardia and Jupp (2000, pp. 222-223):
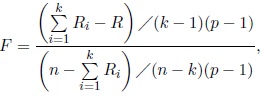 |
(21) |
where Ri is resultant length of the ith sample and R is the resultant length of the global sample. The F -statistic has under H 0 approximately the F(k−1)(p−1),(n−k)(p−1) distribution for large κ.
4.1. Simulation Study
We generated samples of size n from a mixture of equal proportions of two Fisher distributions F (e3, κ) and F (µ, κ), with a common concentration parameter κ. We considered without loss of generality, e3 = (0, 0, 1)T and µ = (0, (1 − cos2 θ)1/2 , cos θ)T, where θ is the angle between µ and e3. Should other mean directions have been used, which form an angle θ, the same results would have been obtained. We considered two sample sizes n = 20, 40, several angles of separation between the two components, θ = 30o, 90o, 150o and two values of the common concentration parameter κ = 5, 10.
For generating observations from the Fisher distribution, we used the method given in Wood (1994) [17A. Wood, "Simulation of the von Mises-Fisher distribution", Commun. Stat. Simul. Comput., vol. 23, no. 1, pp. 157-164.
[http://dx.doi.org/10.1080/03610919408813161] ]. We supposed that the parameters of the mixture are unknown and we estimated these parameters based on each generated sample, using the three variants of the EM algorithm (soft-movMF, hard-movMF and stochastic EM) described in Subsection 3.1, and the dynamic clusters type algorithm described in Subsection 3.2. We obtained the estimates of the concentration parameters and the angle between the estimated mean directions, indicated in the Table 1. for the sample size of 20 and concentration parameters of the components equal to 5 or 10 and in Table 2 for the sample size of 40 and concentration parameters of the components equal to 5. In these tables, we also present for each sample, the classification results (confusion matrix), the sizes of the groups and within-groups and between-groups variability measures for the final solution, which were obtained by the expressions given in the previous subsection, where the concentration parameters were replaced by their maximum likelihood estimates. We note that when the angle θ = 30o, i.e., the components are poorly separated, the stochastic EM algorithm did not converge for any run. When the components are reasonably or well-separated. i.e., θ = 90° or θ = 150°, all algorithms lead to the same solution, in general.
From the results indicated in Tables 1-2, we conclude the following:
- The algorithms gave the same solution when the two components are well separated, that is, when θ = 90° for κ = 5 and when θ = 90° or θ = 150° for κ = 10. Therefore, in these cases, the confusion matrix is the same and the variability measures coincide for all the algorithms, as well as the estimates of the concentration parameters and the estimate of the angle between the mean directions.
- When the concentration of the components increases, the rate of misclassified observations decreases (or remains equal) and the between-groups variability increases, along with the F -statistic for components with moderate or large separation.
- For each algorithm, the rate of misclassified observations decreases as the separation between the components increases, and for well-separated components, this error rate is equal to 0. This error rate decreases or is equal to 0 when the sample size increases.
- For each algorithm, the between-groups variability increases as the separation between the two components increases and for well separated components, the between-groups variability exceeds largely the within-groups variability. The F -statistic also increases when the angle between the mean directions of the components increases.
- When the sample size increases, the between-groups variability and F -statistic increase for moderate or large separation of the components of the mixture.
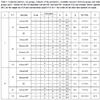
Confusion matrices, size groups, estimates of the parameters, variability measures (between-groups and within-groups) and F -statistic for the EM algorithm (soft-movMF, hard-movMF, stochastic EM) and dynamic clusters algorithm (DC), for the sample size of 20 and concentrations equal to 5 or 10 (*: the results for the other three methods are equal).

Confusion matrices, size groups, estimates of the parameters, variability measures (between-groups and within-groups) and F-statistic for the EM algorithm (soft-movMF, hard-movMF, stochastic EM) and dynamic clusters algorithm (DC), for the sample size of 40 and concentrations equal to 5 (*: the results for the other three methods are equal).
4.2. Example
We used the spherical data given in Wood (1982) [18A. Wood, "A bimodal distribution on the sphere", Appl. Stat., vol. 31, no. 1, pp. 52-58.
[http://dx.doi.org/10.2307/2347074] ], which consist of a set of 33 estimates of a previous magnetic pole position of the earth obtained using palaeomagnetic techniques. Each estimate is associated with a different site, the 33 sites being spread over a large of Tasmania. As the data appear to fall into two main groups, Wood (1982) [18A. Wood, "A bimodal distribution on the sphere", Appl. Stat., vol. 31, no. 1, pp. 52-58.
[http://dx.doi.org/10.2307/2347074] ] estimated the parameters of a bimodal model for the data.
We obtained a partition of these data into two groups based on the estimation of a mixture of two Fisher distributions through the three variants of the EM algorithm (soft-movMF, hard-movMF and stochastic EM) described in Subsection 3.1 and dynamic clusters type algorithm described in Subsection 3.2. For obtaining the final solutions of the variants of the EM algorithm, we used the R package, movMF. For the dynamic clusters type algorithm, as it depends on the initial solution, we considered several initial partitions randomly chosen for the algorithm and for all initial partitions, the algorithm converged and the final solution obtained was the same. The final solutions obtained with the algorithms are given in the Table 3.
The solutions obtained with the several algorithms do not coincide, probably because in this case the components are not well-separated (the estimated angle between the mean directions is around 30o). But, the solutions obtained with soft-movMF, stochastic EM and dynamic clusters algorithm are rather similar, as we may observe for these solutions, a large number of observations is stable in the partitions, i.e., 87.8% of the observations stay always together in the same group. We compared the solutions obtained in the algorithms through the between-groups variability measure and F -statistic, where we estimated the concentration parameters. (See Table 4).
The solution obtained in stochastic EM is preferable in what concerns to the between-groups variability, but considering the F -statistic, the solution obtained with dynamic clusters algorithm is preferable.
CONCLUDING REMARKS
The simulations revealed that only for poorly or moderately separated components, the variants of the EM algorithm and the dynamic clusters type algorithm lead to different solutions in general. For very well separated components, the algorithms seem to originate the same result. Additionally, the larger concentration parameters associated with the components, greater is the tendency to obtain the same solution for the algorithms.
For each algorithm, as expected, the between-groups variability and the F -statistic increase when the separation between components increases or when the concentration of components increases, since these components are not badly separated (i.e., the angle θ is 30o).
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The author declares no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
• The author is grateful to the referees of this journal for their helpful comments.
• This work is financed by the ERDF European Regional Development Fund through the COMPETE Programme (operational programme for competitiveness) and by National Funds through the FCT Fundação para a Ciência e a Tecnologia (Portuguese Foundation for Science and Technology) within project FCOMP-01-0124-FEDER- 037281.
APPENDIX A
Derivation of the Expected Log-Likelihood of the Complete Sample
The vectors zi are independent and have multinomial distribution with parameters (1, π1,...πk) and the probability density function is given by
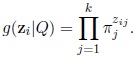 |
The density function of xi|zi is given by
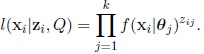 |
Then, the density function of (xi, zi) is defined by the product
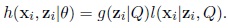 |
Replacing the densities g (zi|Q) and l (xi|zi, Q) in the previous expression, we obtain
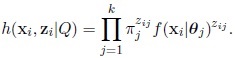 |
The complete data log-likelihood of (x1, x2, ..., xn, Z) is given by
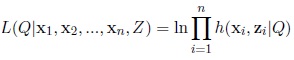 |
and replacing h (xi, zi|Q), we obtain the expression
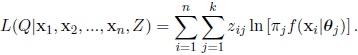 |
The density function of zi|xi is given by
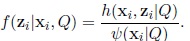 |
Replacing the densities h and ψ, we obtain
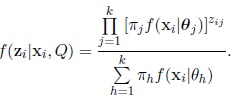 |
The expected value of Zij |xi is given by the expression
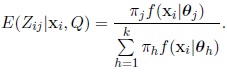 |
This expected value is the aposteriori probability of xi belonging to Cj , which we denote by tj (xi) . Then, the expected complete data log-likelihood may be written as
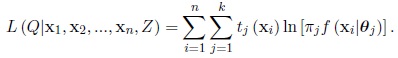 |
APPENDIX B
Derivation of the Maximum Likelihood Estimators
First, consider the function L1 (Q) subject to the constraint µTj µj = 1
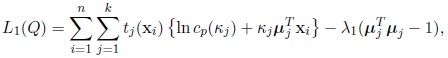 |
where λ1 is a Lagrange multiplier and tj (xi) is defined by (7). The maximum likelihood estimator of µj is the solution of the following equation
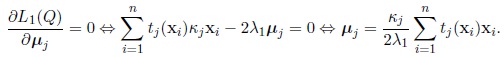 |
As µTj µj = 1; then the Lagrange multiplier is given by
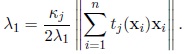 |
So the maximum likelihood estimator of µj in the (m + 1)th iteration,
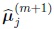 is given by
is given by
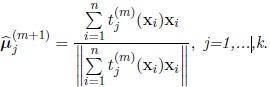 |
Second, the maximum likelihood estimator of κj is the solution of the equation
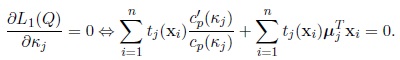 |
Let 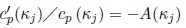 and then the previous equation may be written as
and then the previous equation may be written as
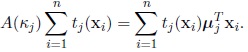 |
Replacing µj by
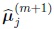 , the maximum likelihood estimator of κj obtained in the (m + 1)th iteration,
, the maximum likelihood estimator of κj obtained in the (m + 1)th iteration,
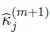 is the solution of the equation
is the solution of the equation
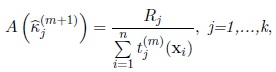 |
where Rj is the length of the vector
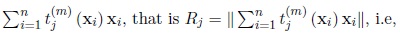 ,
,
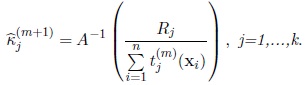 |
Third, consider the function, L2 (Q) subject to the constraint
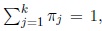 that is, maximize
that is, maximize
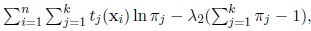 where λ2 is a Lagrange multiplier. The maximum likelihood estimator of πj is the solution of the equation
where λ2 is a Lagrange multiplier. The maximum likelihood estimator of πj is the solution of the equation
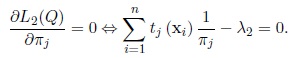 |
Summing the last equation from j = 1 to k, we obtain λ2 = n. Then the maximum likelihood estimator of πj in the (m + 1)th iteration,
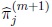 is given by
is given by
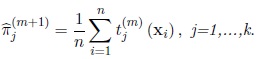 |
APPENDIX C
Derivation of the Common Concentration Estimator
When all concentration parameters κi are equal to κ, the expression L1(Q) given by (5) reduces to
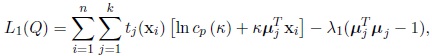 |
The estimator of κ is the solution of the equation
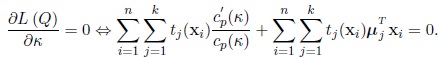 |
The last equation is equivalent to the following one
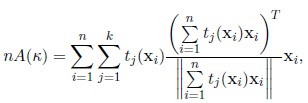 |
where
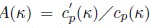 . The maximum likelihood estimator of κ in the (m + 1)th iteration,
. The maximum likelihood estimator of κ in the (m + 1)th iteration,
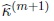 is the solution of the equation
is the solution of the equation
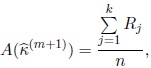 |
where Rj is defined as before.
REFERENCES
| [1] | I.S. Dhillon, and D.S. Modha, "Concept Decompositions for large Sparse Text Data Using Clustering", Mach. Learn., vol. 42, no. 1, pp. 143-175. [http://dx.doi.org/10.1023/A:1007612920971] |
| [2] | K. Hornik, I. Feinerer, M. Kober, and C. Buchta, "Spherical k-Means Clustering", J. Stat. Softw., vol. 50, no. 10, pp. 1-21. [http://dx.doi.org/10.18637/jss.v050.i10] [PMID: 25317082] |
| [3] | D. Peel, W.J. Whiten, and G.J. McLachlan, "Fitting mixtures of Kent distributions to aid in joint set identification", J. Am. Stat. Assoc., vol. 96, no. 453, pp. 56-63. [http://dx.doi.org/10.1198/016214501750332974] |
| [4] | J.T. Kent, "The Fisher-Bingham distribution on the sphere", J. R. Stat. Soc. B, vol. 44, no. 1, pp. 71-80. |
| [5] | J-L. Dortet-Bernadet, and N. Wicker, "Model-based clustering on the unit sphere with an illustration using gene expression profiles", Biostatistics, vol. 9, no. 1, pp. 66-80. [http://dx.doi.org/10.1093/biostatistics/kxm012] [PMID: 17468207] |
| [6] | A. Banerjee, I.S. Dhillon, J. Ghosh, and S. Sra, "Clustering on the unit hypersphere using von Mises-Fisher distributions", J. Mach. Learn. Res., vol. 6, pp. 1345-1382. |
| [7] | G. Celeux, and G. Govaert, "A classification EM algorithm for clustering and two-stochastic versions", Comput. Stat. Data Anal., vol. 14, no. 3, pp. 315-332. [http://dx.doi.org/10.1016/0167-9473(92)90042-E] |
| [8] | A. Figueiredo, and P. Gomes, "Clustering of variables based on Watson distribution on hypersphere: A comparison of algorithms", Communications in Statistics -Simulation and Computation., vol. 44, no. 10, pp. 2622-2635.Special issue: Joint Meeting of y-BIS and jSPE, 2015. |
| [9] | E. Diday, and A. Schroeder, "New approach in mixed distributions detection, Révue Française D’Automátique", Automatique Informatique Recherche Operationelle, vol. 10, no. 6, pp. 75-106. [http://dx.doi.org/10.1051/ro/197610V200751] |
| [10] | A.P. Dempster, N.M. Laird, and D.B. Rubin, "Maximum likelihood from incomplete data via the EM algorithm (with discussion)", J. R. Stat. Soc. B, vol. 3, no. 1, pp. 1-38. |
| [11] | R. Redner, and W. Homer, "Mixture Densities, Maximum Likelihood, EM algorithm", J. R. Stat. Soc. B, vol. 39, no. 2, pp. 1-38. |
| [12] | K.V. Mardia, and P.E. Jupp, Directional Statistics., John Wiley and Sons: Chichester, . |
| [13] | K. Hornik, and B. Grun, "movMF: An R Package for fitting mixtures of von Mises-Fisher distributions", J. Stat. Softw., vol. 58, no. 10, pp. 1-26. [http://dx.doi.org/10.18637/jss.v058.i10] |
| [14] | G.S. Watson, "Analysis of dispersion on a sphere", Monthly Notices of the Royal Astronomical Society Geophysical, vol. 7, no. 4, pp. 153-159. [http://dx.doi.org/10.1111/j.1365-246X.1956.tb05560.x] |
| [15] | G.S. Watson, and E.J. Williams, "On the construction of significance tests on the circle and the sphere", Biometrika, vol. 43, no. 3-4, pp. 344-352. [http://dx.doi.org/10.1093/biomet/43.3-4.344] |
| [16] | D. Harrison, G.K. Kanji, and R.J. Gadsden, "Analysis of variance for circular data", J. Appl. Stat., vol. 13, no. 2, pp. 123-138. [http://dx.doi.org/10.1080/02664768600000021] |
| [17] | A. Wood, "Simulation of the von Mises-Fisher distribution", Commun. Stat. Simul. Comput., vol. 23, no. 1, pp. 157-164. [http://dx.doi.org/10.1080/03610919408813161] |
| [18] | A. Wood, "A bimodal distribution on the sphere", Appl. Stat., vol. 31, no. 1, pp. 52-58. [http://dx.doi.org/10.2307/2347074] |