- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Virtual Reality Journal
(Discontinued)
ISSN: 1875-323X ― Volume 3, 2014
A Review of Spatial Sound for Virtual Environments and Games with Graphics Processing Units
Foad Hamid 1, Bill Kapralos*, 2
Abstract
The generation of spatial audio and audio processing in general using traditional software-based methods and techniques is computationally prohibitive thereby limiting the number of, and type of auditory effects that can be incorporated into applications. In contrast to consumer-grade audio cards, the graphics processing units (GPUs) of video cards have moved away from the traditional fixed-function 3D graphics pipeline towards a flexible general-purpose computational engine that can currently implement many parallel algorithms directly using the graphics hardware resulting in tremen¬dous computational speed-ups. Various spatial audio applications are well suited for GPU-based processing providing developers of virtual environments and games with the possibility of incorporating real-time, spatial audio into their simulations. This paper presents an overview of the research efforts that have utilized the GPU for the implementation of spatial sound for virtual environments and games. Approaches to GPU-based spatial sound are summarized and their advantages and disadvantages are presented
Article Information
Identifiers and Pagination:
Year: 2009Volume: 1
First Page: 8
Last Page: 17
Publisher Id: TOVRJ-1-8
DOI: 10.2174/1875323X01002010008
Article History:
Received Date: 5/7/2009Revision Received Date: 30/7/2009
Acceptance Date: 1/9/2009
Electronic publication date: 3 /9/2009
Collection year: 2009
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
* Address correspondence to this author at the Faculty of Business and Information Technology, University of Ontario Institute of Technology, 2000 Simcoe Street North, Oshawa, Ontario, Canada, L1H 7K4; Email: bill.kapralos@uoit.ca
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 5-7-2009 |
Original Manuscript | A Review of Spatial Sound for Virtual Environments and Games with Graphics Processing Units | |
1. INTRODUCTION
A virtual (or three-dimensional (3D), or spatial) audio system (or audio display) allows a listener to perceive the position of a sound source(s), emanating from a static number of stationary loudspeakers or a pair of headphones, as coming from arbitrary locations in three-dimensional space. Spatial sound technology goes far beyond traditional stereo and surround sound techniques by allowing a virtual sound source to have such attributes as left-right, back-forth, and up-down [1]. Incorporating spatialized auditory information in an immersive virtual environment and video games is beneficial for a variety of reasons. Spatial auditory cues can add a better sense of “presence” or “immersion”, compensate for poor visual cues (graphics), and at the very least, add a “pleasing quality” to the simulation [2, 3]. Despite these benefits and despite the fact that spatial sound is a critical cue to the perception of our environment, it is often overlooked in immersive virtual environments and video games where, historically, emphasis has been placed on the visual senses [1, 4]. That being said, the generation of spatial sound for dynamic, and interactive virtual environments using traditional software-based methods and techniques is computationally very expensive except for trivial environments which are typically of little use.
Driven by the gaming industry, consumer computer graphics hardware has greatly advanced in recent years, out performing the computational capacity of central processing units (CPUs). A graphics processing unit (GPU) is a dedicated graphics rendering device whose purpose is to provide a high performance, visually rich, interactive 3D experience by exploiting the inherent parallelism in the feed-forward graphics pipeline [5]. In contrast to the processors on-board consumer-grade audio cards, the GPUs available on all modern video cards have moved away from the traditional fixed-function 3D graphics pipeline towards a flexible general-purpose computational engine that can currently implement many parallel algorithms directly using graphics hardware. This results in tremendous computational speed-ups. Due to a number of reasons including the explosion of the consumer video game market and advances in manufacturing technology, GPUs are, on a dollar-per-dollar basis, the most powerful computational hardware, providing “tremendous memory bandwidth and computational horsepower” [6]. GPUs are also becoming faster and more powerful very quickly, far exceeding Moore’s Law applied to traditional microprocessors [7]. In fact, instead of doubling every 18 months as with CPUs, GPU performance increases by a factor of five every 18 months or doubles every eight months [8]. In contrast to older GPUs that contained a fixed-function pipeline with output limited to 8-bits-per-color-channel, current GPUs include fully programmable processing units which support vectorized floating point operations [6]. As a result, a number of high level languages have been introduced to allow for the control of vertex and pixel pipelines [9].
Given the typically large computational requirements associated with spatial sound generation and audio processing in general, the GPU is an economical and computationally feasible alternative to traditional software-based methods and techniques. With respect to the potential computational efficiencies that GPUs offer and their applicability to audio processing, this paper reviews the research efforts that have examined the application of the GPU to the generation of spatial sound and audio processing for virtual environments and video games. Various approaches will be summarized and in the process of doing so, advantages, disadvantages, limitations, drawbacks, and trade-offs will be presented. Being an overview, this paper does not introduce any new research results. Rather, it presents a general review of GPU-based spatial sound and audio processing compiling the relevant information available from a variety of sources, providing the reader with a summary of the technological literature relevant to the creation of spatial sound using the GPU. The foundation of spatial sound rests on the ability to control the auditory signals arriving at the listener’s ears such that these signals are perceptually equivalent to the signals the listener would receive in the environment being simulated [10]. However, a review of human auditory perception is beyond the scope of this work (an excellent overview of human auditory perception is available in [11]). Similarly, a complete overview of spatial sound will not be described here but a recent review is available in [12].
1.1. Paper Organization
The remainder of this paper is organized as follows. Section 2 provides a brief introduction and background information to graphic processing units (GPUs). A brief description of general purpose GPU or GPGPU whereby the GPU is applied to non-graphics applications, is also provided with an emphasis on general audio-based methods and techniques. Section 3 begins with an introduction to auralization followed by various research efforts that have applied GPU technology to auralization and more specifically, to the generation of spatial sound. Finally, concluding remarks and possible future directions of GPU-based spatial sound technology are discussed in Section 4.
2. BACKGROUND
In computer graphics, rendering is accomplished using a graphics pipeline architecture whereby rendering of objects to the display is performed in stages and each stage is implemented as a separate piece of hardware. The input to the pipeline is a list of vertices expressed in object space while the output is an image in the framebuffer. The stages of the pipeline and their operation are as follows (see also Fig. 1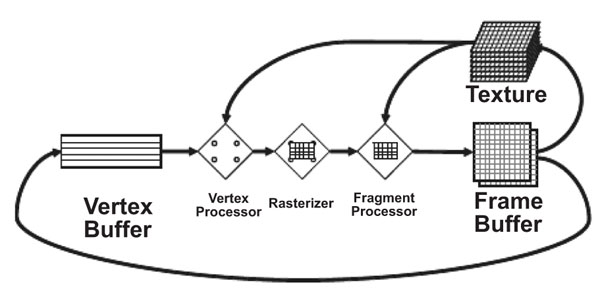 ) [6]:
) [6]:
 |
Fig. (1) The traditional computer graphics pipeline. Rendering is divided into a number of stages and each stage is implemented as a separate piece of hardware. Reprinted from [16]. |
Vertex Stage i) Transformation of each (object space) vertex into screen space, ii) formation of triangles from the vertices, and iii) per-vertex lighting calculations.
Rasterization Stage i) Determination of the screen position covered by each of the triangles formed in the previous stage, and ii) interpolation of vertex parameters across the triangle.
Fragment Stage Calculation of the color for each fragment output in the previous stage. Often, the color values come from textures which are stored in texture memory. Here the appropriate texture address is generated and the corresponding value is fetched and used to compute the fragment color.
Composition Stage Pixel values are determined from the fragments.
In contrast to the “traditional” fixed-function pipelines with “modern” (programmable) GPUs, both the vertex and fragment stages are user-programmable. Programs written to control the vertex stage are known as vertex programs or vertex shaders while programs written to control the fragment stage are known as fragment programs or fragment shaders. Early on, these programs were written in assembly language. However, higher level languages have been introduced, including Microsoft’s high level shading language (HLSL), OpenGL shading language (GLSL) [13], NVIDIA’s compute unified device architecture (CUDA), and NVIDIA’s Cg [14]. Generally, the input to both of these programmable stages is four-element vectors where each element represents a 32-bit floating point number. The vertex stage will output a limited number of 32-bit, four element vectors while the fragment stage will output a maximum of four floating point, four element vectors that typically represent color. The fragment stage is capable of fetching data from texture memory (i.e., perform memory gather) but cannot alter the address of its output which is determined before processing of the fragment begins (i.e., incapable of memory scatter). In contrast, within the vertex stage, the position of input vertices can be altered, thus affecting where the image pixels will be drawn (i.e., the vertex stage supports both memory gather and memory scatter) [6]. In addition to vertex and fragment shaders, Shader Model 4.0 currently supported by Direct3D 10 and OpenGL 3.0 defines a new type of shader, the geometry shader. A geometry shader receives input from the vertex shader, can be used to create new geometry and is capable of operating on entire primitives [15].
In order to take advantage of the power inherent in GPUs in addition to their relatively low cost, recently, a number of efforts have investigated the use of GPUs to a variety of non-computer graphics applications. Collectively, this effort is known as “general purpose computing on the GPU” (GPGPU) and given the flexibility of GPUs, has led to a number of GPU-based applications, outside the scope for which GPUs were originally designed for [6]. Examples include solving differential equations and general linear algebra problems [6], applications in computer vision [17], image processing [18], implementation of fast Fourier transform [9], the simulation of dynamic phenomena described by partial differential equations (e.g., boiling, convection, and chemical reaction diffusion) [19], database and data mining [20, 21], and audio processing. That being said, currently GPUs do not support integers and associated operations including bit-wise logical operations making them ill-suited for a operations requiring such features (e.g., cryptography). A thorough review including a detailed summary of GPGPU-based applications is provided by Owens et al. [6] and will therefore not be provided here.
2.1. GPU-based Sound Processing
GPUs have also been applied to a wide variety of audio-based applications. Von Tycowicz and Loviscach [22] describe the implementation of a flexible virtual drum that is simulated in real-time and with low latency on the GPU. The drum is modeled using a 64 × 64 mesh where each point is connected to neighbor points with springs and dampers. Using the GPU has allowed the resolution of the mesh to be increased. The user can modify the shape of the drum in real-time. A MIDI controller with 16 pressure points is used for pressure recognition and a finite difference method is employed to synthesize sound based on location and pressure information.
Matsuyama et al. [23], describe a method for the automatic generation of real-time sound for graphics-based animation of sparks to simulate thunder and lighting effects. The implementation also makes use of GPU-based numerical methods introduced by Kruger and Westermann [24].
There have been a number of efforts to utilize the GPU for the implementation of a variety of digital signal processing methods and techniques motivated by the fact that most DSP functions are suitable for GPU-based processing (i.e., they are parallelizable, are highly arithmetic intense, have limited data dependency, and make use of multiply-add (MADD) calculation units that are part of the GPU architecture). Using the Cg shading language, Whalen [25] implements seven common audio functions: chorus, compress, delay, high-pass filter, low-pass filter, noise-gate and normalization. A performance comparison was made between the GPU and corresponding CPU implementation using a Pentium IV (3.0 GHz CPU) and an NVIDIA GeForce FX 5200 video card. The GPU showed better performance for several of the functions (compress and chorus with speedups of up to a factor of four). However, the CPU implementation was better for other functions (high-pass and low-pass filters). It was suggested that GPU performance was poorer for some algorithms given the implementation of these algorithms was not suitable for GPU implementation given that they required (computationally expensive) texture access. With more modern video cards, texture access has been improved and this will undoubtedly lead to greater improvements in these methods. Trebien and Oliveira [26] propose a GPU-based method for real-time sound generation and multichannel audio processing to be used in live music performances. The motivation behind the approach comes from the observation that many DSP units include several independent units that work in parallel. They mapped a network model of virtually interconnected software modules to the GPU graphics pipeline. In their design, audio blocks are stored in texture memory and are passed between modules as texture coordinates. An audio sample corresponds to a fragment with its amplitude stored as a luminance value. Since GPU memory access is restricted, they use multi-pass access to implement a “ping-pong” model whereby a register is write-only in one pass and becomes read-only in the next pass. Using this approach, several common audio algorithms such as additive synthesis (used to generate new sound waves from sinusoids), sawtooth, square or triangular waves, feedback delay, gain, and envelope shaping (a variant of amplitude modulation that scales each sample by a fast varying factor) were implemented. The system was tested on a computer with an AMD 2.21GHz CPU and an NVIDIA GeForce 8800 GTX video card. The GPU showed speed-ups of up to four orders of magnitude (17,641×) over a CPU implementation. It is suggested that in the future, additional algorithms that implement various filters and frequency modulation can be developed using this approach.
Gallo and Tsingos [27] considered the application of GPUs to variable delay-line (delaying the signal of each sound source by the propagation time of the sound wave) and filtering (filtering the audio signal to simulate directivity functions, occlusions, and interaction with the medium of propagation). Variable delay line and filtering are two common spatial audio processing operations [27]. Delaying the signal involved re-sampling the signal at non-integer index values and was performed on the GPU using texture re-sampling. Filtering was performed using a four-band equalizer and implemented on the GPU using a four-component dot-product. Sound signals were stored as RGBA textures where each of the components held a band-pass copy of the original signal. Experimental results indicated a performance increase associated with the GPU-based implementation when compared to optimized software implementations on a standard CPU. Despite the promising results, their work also showed that there are still a number of shortcomings that limit the efficient use of GPU processors for “mainstream” audio processing. In particular, long 1D textures cannot be accessed easily, and infinite impulse response filters (commonly used in audio processing) cannot be implemented efficiently. The scheme was implemented on a Pentium IV 1.8 GHz CPU and an ATI Radeon 5700 graphics card. Each sound event was a three sub-band monaural signal at 44.1 kHz and was processed in blocks of 1024 samples. A scene with approximately 70,000 polygons was rendered concurrently with audio. One shortcoming of the implementation is that since each cluster’s signals are premixed, bus traffic is increased. Also, because the GPU only supported 8-bit mixing as opposed to the CPU’s 32-bit support, the quality of the GPU rendered signal was not as good as the signal processed on the CPU. However, the processing required 38% of the CPU’s processing time. Without the use of the GPU, the scheme can render 50 to 60 sources while using the GPU allows for rendering of more than 160 sources possible.
Modal synthesis is a physically-based audio synthesis method to model sounds made by objects through a bank of damped harmonic oscillators that are excited by an external stimulus [28]. Zhang et al. [29] present a two-phase GPU-based modal synthesis method based on a bank of damped harmonic oscillators that are excited by an external stimulus to model a vibrating object. Two sets of factors affect the system: i) static factors, which are independent of interaction and include geometry and material properties, and ii) dynamic factors, which depend on the interaction and include contact location and external force. The first set of factors are taken into account during a pre-computation stage and the second set are incorporated during run-time. Each of the modes is precalculated in parallel and stored in 2D textures for runtime retrieval. 10-30 sampling contact locations are employed for common objects. In the first step, the response for each individual mode for all sounding objects is calculated and is implemented as a dot product between two vectors (performed efficiently on the GPU). The second step involves summarizing the responses from the objects; it is essentially a reduction operation that is implemented as a multi-pass “ping-pong” process. For a texture with N × N resolution, log2 2N rendering passes are performed until the final sum is obtained in a single pixel. Some experimental results are presented but the experiments were restricted to a maximum of 5000 modes due to hardware restrictions (Pentium IV 2.8 GHz CPU and an NVIDIA GeForce 6800 GT video card). Although performance was not ideal, it is suggested that this is due to the slow AGP memory bus of the 6800 GT video card and results will improve by employing a video card that employs a PCI-Express bus.
3. GPU-BASED AURALIZATION
Kleiner, Dalenbäck, & Svensson [30] define auralization as “the process of rendering audible, by physical or mathematical modeling, the sound field of a source in space in such a way as to simulate the binaural listening experience at a given position in the modeled space”. The goal of auralization is to recreate a particular listening environment taking into account the environmental acoustics (i.e., the “room acoustics”) and the listener’s characteristics. Auralization is typically defined in terms of the binaural room impulse response (BRIR). The BRIR represents the response of a particular acoustical environment and human listener to sound energy and captures the room acoustics for a particular sound source and listener configuration. The recorded response then forms the basis of a filter that is used to process source sound material (anechoic or synthesized sound) via a convolution operation before presenting it to the listener. When the listener is presented with this filtered sound, the direct and reflected sounds of the environment are reproduced in addition to directional filtering effects introduced by the original listener [31].
Although interlinked, for simplicity and reasons of practicality, the room response and the response of the human receiver are commonly determined separately and combined via a post-processing operation to provide an approximation to the actual BRIR [30]. The response of the room is known as the room impulse response (RIR) and captures the reflection properties (reverberation), diffraction, refraction, sound attenuation, and absorption properties of a particular room configuration (i.e., the “room acoustics”). The response of the human receiver captures the direction dependent effects introduced by the listener due to the listener’s physical make-up (e.g., pinna, head, shoulders, neck, and torso) and is known as the head related transfer function (HRTF). HRTFs encompass various sound localization cues including interaural time differences (ITDs), interaural level differences (ILDs), and the changes in the spectral shape of the sound reaching a listener. The HRTF modifies the spectrum and timing of sound signals reaching each ear in a location-dependent manner [32]. The process of collecting a set of individualized HRTFs is an extremely difficult, time consuming, tedious, and delicate process requiring the use of special equipment and environments such as an anechoic chamber. Although the HRTF of individuals can vary greatly, it is impractical to use individualized HRTFs and as a result, generalized (or generic) non-individualized HRTFs are often used instead. Non-individualized HRTFs can be obtained using a variety of methods such as measuring the HRTFs of an anthropomorphic “dummy” head, or of an above average human localizer or averaging the HRTFs measured from several different individuals (and/or “dummy heads”). Several non-individualized HRTF datasets are freely available [33-36] (see [12] for greater details regarding the problems associated with non-individualized HRTFs).
The output of the methods used to determine the HRTF and the RIR is typically a transfer function which forms the basis of a filter that can be used to modulate source sound material (i.e., anechoic or synthesized sound) via a convolution operation which is still primarily performed in software in the time domain. When the filtered sounds are presented to the listener, in the case of HRTFs, they create the impression of a sound source located at the corresponding HRTF measurement position while when considering the RIR, the filtered sounds recreate a particular acoustic environment. However, convolution is a computationally expensive operation especially when considering the long filters associated with HRTFs and RIRs (filters with 512 coefficients are not uncommon) thus limiting their use to non-real-time applications. Performance improvements can be made by performing the convolution operation in the frequency domain [37]. In order to accomplish this, the input and filters must be converted to their frequency domain representation using the fast Fourier transform; a time consuming process when performed in software making it impractical for real-time, interactive use. Recent work in image processing has established a GPU-based convolution method capable of performing a two-dimensional convolution operation in real-time [38, 39]. In addition to software-based convolution methods, programmable DSP cards are available which allow for hardware-based convolution thus greatly improving performance. However, these cards are very specialized and typically only available to product developers and not the general consumer [27].
Cowan and Kapralos presented a GPU-based convolution method using the OpenGL shading language (GLSL) [40, 41]. A comparison of the computational running time requirements for both the conventional (software-based) and GPU-based convolution method was made by measuring the computational time requirements when convolving a particular input signal with an HRTF using two video cards (GPUs) for further comparisons: the NVIDIA GTX 8800 and the NVIDIA GTX 280 which supports double precision floating point operations. Both video cards supported real-time convolution for an input signal whose size ranged from 5,000 to 60,000 and a filter containing 200 samples; approximately four and two milliseconds (including any required CPU processing time) for the GTX 8800 and the GTX 280 respectively, in contrast to the software-based method whose computational requirements increased linearly with increasing input size (ranging from approximately 4 to 25 ms). With a constant running time of 2 ms for the convolution operation (the NVIDIA GTX 280 video card), realistic spatial auditory cues can be incorporated into video games and virtual environments in real-time.
Rather than using measured HRTFs (individualized or non-individualized), Röber [42] et al. describe an alternative approach whereby the HRTF is modeled using GPU-based ray tracing techniques using a 3D mesh model of the upper torso including the pinna. The HRTFs are approximated by simulating an impulse response that is recorded by a semi-spherical surface placed inside the ear canal of the model. The 3D mesh can be changed easily making the method suitable for measuring individual HRTFs. The sound source is approximated by a point light and the microphone is represented by a hemispherical camera surface. To simplify computation, the algorithm is applied to high frequencies only, since high frequencies hold important spatialization cues. The lower frequencies usually bend around the head and are not as important for spatialization and therefore are approximated by amplitude and time shifts. Verification of the method with human participants is required to compare the resulting HRTFs with existing non-individualized HRTFs given the assumptions made (e.g., ignoring the lower frequencies).
3.1. GPU-Based Acoustical Modeling - Modeling the RIR
There are two major approaches to computationally modeling the RIR i) wave-based modeling where numerical solutions to the wave equation are used to compute the RIR, and ii) geometric modeling where sound is approximated as a ray phenomenon and traced through the scene to construct the RIR.
3.1.1. Wave-Based Modeling
The objective of wave-based methods is to solve the wave equation (also known as the Helmholtz-Kirchoff equation [43]), to recreate the RIR that models a particular sound field. An analytical solution to the wave equation is rarely feasible hence wave-based methods use numerical approximations such as finite element methods, boundary element methods, and finite difference time domain methods instead [44]. Numerical approximations sub-divide the boundaries of a room into smaller elements (see Fig. 2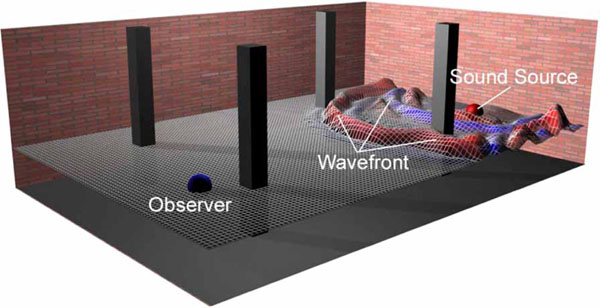 ).
).
 |
Fig. (2) Wave-based acoustical modeling. Reprinted from [45]. |
By assuming that the pressure at each of these elements is a linear combination of a finite number of basis functions, the boundary integral form of the wave equation can be solved [43]. The acoustical radiosity method, a modified version of the image synthesis radiosity technique, is an example of such an approach [46, 47]. The numerical approximations associated with wave-based methods are computationally prohibitive making the use of traditional software-based methods impractical except for the simplest static environments. Aside from basic or simple environments, such techniques are currently beyond our computational ability for real-time, interactive virtual environment and video game applications.
That being said, the processing power inherent in GPUs has been exploited in a number of wave-based methods. Röber et al. present a (low-frequency) wave-based acoustical modeling method that made use of the GPU and in particular, fragment shaders, 3D textures, and the OpenGL framebuffer objects extension, in order to take advantage of the inherent parallelism of wave-based solutions to acoustical modeling [48]. The one-dimensional mesh is extended by constructing a digital mesh from bi-linear delay lines that connect junctions that act as temporal and spatial sampling points. The programmable vertex shader is used to implement computations on a per vertex basis on a 3D space and the fragment shader is used to compute the final pixel color. Waveguide node data is stored in three buffers that are combined into one RGB texture with the data stored in the red and blue components and the geometry and boundary coefficients in the green channel. During each time frame, the fragment shader computes the difference equations for each node in the mesh and stores the result in the buffer. They have used a body centered cubic grid (BCC) which is an hexagonal lattice that requires only 70% of the sampling points compared to the usual rectilinear grid which is a cubic cartesian lattice. This data structure reduces the computation load by √2 and can be decomposed into cubic grids that make the GPU implementation straightforward. The limitations of this approach are a direction dependent dispersion error and the finite mesh resolution to model boundary behavior. Also, the approach implements 2D meshes only. The system was tested on a PC with an AMD64 4000+ dual-core CPU and an NVIDIA GeForce 7900 GT video card and showed speed-ups of factors of from 4.5 to 69 when compared to a software-based implementation. However, the CPU implementation was not optimized.
Tsingos et al. [49] present a new approach for high-quality modeling of first-order sound propagation. The method employs a surface-integral formulation and Kirchhoff approximation, which can be viewed as a hybrid between geometric acoustics (ray tracing) and wave acoustics. In contrast to other sound propagation techniques, it is capable of rendering very complex scenes and implements both diffraction and reflection in a unified manner. The method maps well to graphical hardware since it computes the scattering from detailed, dynamic geometry. It combines the Helmot-Kirchhoff theorem with the Kirchhoff approximation to derive an expression for first order scattering effects. A GPU implementation in this case is suitable because the above formulation is similar to the reflective shadow map that is introduced to compute interactive first order global illumination effects. It also allows the implementation of a level-of-detail approach that reduces the geometry processing for audio rendering while preserving the scattering behavior of complex surfaces by allowing bump or displacement mapping. There are two steps in the computation: i) during the first step, all scattering surfaces visible from the source are determined and sampled, and ii) in the second step, the evaluation and summation of the differential contribution of clocked plus reflected wavefronts for all surface samples is made. The first task is implemented using a computer graphics shadow mapping source-view technique that renders the scene from the location of the sound source. For the second task, a hierarchal integration method known as “mip-mapping” is used that requires log(rez)/log(k) render passes where rez is the rendering resolution and k is the reduction factor. At each pass a k × k block of values is summed to give a single value which is recursively integrated in the next pass until the value of the integral is reached. Both visual rendering and the calculation of audio scattering coefficients are done on the GPU. The auralization is achieved by re-equalizing performed asynchronously on the CPU. The method was tested on a Pentium IV 3.4GHz CPU and an NVIDIA GeForce 8800 GTX graphics card and was compared to a C++ implementation on the CPU. For an interactive scenario the GPU-based method was found to be 40 times faster. The limitations of this method are that it is prone to aliasing due to insufficient sampling at high frequencies and is also limited to first order scattering and therefore cannot be used for some audio effects such as reverberation and occlusion. Also, by using a frequency domain approach, essential for an efficient implementation, this method introduces an approximation because of the limited number of frequency bands.
Despite the progress to-date, plenty of work remains to allow for real-time, accurate, wave-based acoustical modeling on the GPU. Of course, depending on the application, completely and faithfully recreating the acoustics of a particular environment may not be necessary; hearing is a perceptual process and there is no one-to-one mapping between physical acoustical phenomena and our perception of these phenomena. Therefore, accuracy may not always be necessary. Greater work needs to be conducted to examine this issue more carefully. Finally, although the number of efforts investigating wave-based acoustical modeling using the GPU are limited, extensive work has been carried out using such techniques for the computation of global illumination. A number of wave-based techniques utilizing the GPU are available including radiosity [50], etc. If suitably modified, these techniques could be applied to acoustical modeling applications.
3.1.2. Geometric-Based Modeling
Many acoustical modeling approaches adopt the hypothesis of “geometric acoustics” that assumes that sound is a ray phenomenon. The acoustics of an environment is then modeled by tracing (following) these “sound rays” as they propagate through the environment while accounting for any interactions between the sound rays and any objects/surfaces they may encounter (see Fig. 3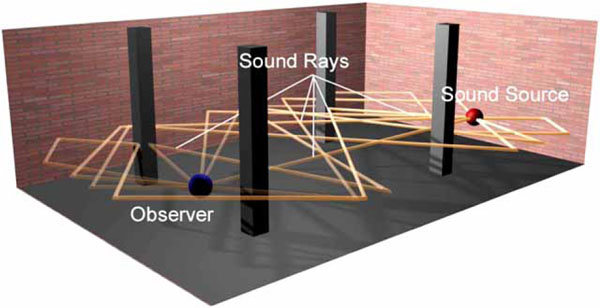 ). Mathematical models are used to account for sound source emission patterns, atmospheric scattering, and the medium’s absorption of sound ray energy as a function of humidity, temperature, frequency, and distance [51]. At the receiver, the RIR is obtained by constructing an echogram which describes the distribution of incident sound energy (rays) over time. The equivalent room impulse response can be obtained by post-processing the echogram [52].
). Mathematical models are used to account for sound source emission patterns, atmospheric scattering, and the medium’s absorption of sound ray energy as a function of humidity, temperature, frequency, and distance [51]. At the receiver, the RIR is obtained by constructing an echogram which describes the distribution of incident sound energy (rays) over time. The equivalent room impulse response can be obtained by post-processing the echogram [52].
 |
Fig. (3) Ray-based acoustical modeling. Reprinted from [45]. |
Audio-based ray tracing using the GPU was implemented by Jedrzejewski to compute the propagation of acoustical reflections in highly occluded environments and to allow for the sound source and the listener to move throughout the simulation without the need for a long pre-computation phase [53]. The method consists of six phases, the first four of which constitute a short pre-computation stage. Jedrzejewski takes advantage of the fact that in acoustics, as opposed to graphics, objects other than walls do not contribute significantly to the sound wave modifications and therefore can be ignored during the computation. Because of this, only polygons that represent walls are taken into account. Furthermore, to make the system more efficient, each ray is intersected with a plane rather than a polygon. A comparison of the method implemented on a GPU and a CPU (2GHz AMD CPU and an ATI Radeon 9800 video card) demonstrated that the GPU-based implementation was much more computationally efficient (32 vs. 500 ms to trace a ray of order 10 on the GPU and CPU respectively). Röber et al. [54] describe a ray-based acoustical modeling method that employed the GPU to allow for real-time acoustical simulations. Their framework was designed along existing (computer graphics) GPU-based ray tracing systems suitably modified to handle sound wave propagation. The system accepts a 3D polygonal mesh of up to 15,000 polygons and pre-processes it into an accessible structure. All signal processing, including HRTF convolution and delay filtering, is programmed as fragment shaders and for each task a single shader is developed. The 3D scene data along with sounds and frequency band decomposed HRTFs are loaded into texture memory and decomposed into 10 bands that are assigned positions and an emittance pattern within the virtual room. Rays are cast into the scene and the value of acoustic energy received per frequency band is accumulated and stored within cubemaps. Each ray is then filtered and delayed using HRTFs according to its position and wavelength. Using this method every cast ray is traced through the virtual scene and its acoustic energy is accumulated and stored per frequency band. A frame-rate of up to 25 fps was achieved using a detailed model of a living room containing 1,500 polygons (using an NVIDIA GeForce 8800 GTX video card).
One problem associated with ray-based approaches involves dealing with the large number of potential interactions between a propagating sound ray and the surfaces it may encounter. A sound incident on a surface may be simultaneously reflected specularly, reflected diffusely, be refracted, and be diffracted. Typical solutions to modeling such effects include the generation and emission of multiple “new” rays at each interaction point. Such approaches lead to exponential running times making them computationally intractable except for the most basic environments and only for very short time periods, particularly for traditional (non-GPU) methods. Although this situation is remarkably improved upon with the use of GPU-based acoustic ray tracing techniques, the problem still remains. As with wave-based methods, greater work can be done to take advantage of the human auditory perception system thus avoiding computations that have minimal (if any), perceptual consequences. For example, it is not necessary to account for non-audible reflections.
Finally, photon mapping is a popular two-pass “particle-based”, probabilistic global illumination method that is independent of the scene geometry [55]. Being probabilistic, the solution can be made more accurate by increasing the number of samples at various points of the computation allowing for an accuracy vs. efficiency trade-off. Despite the computational improvements over many other global illumination methods such as ray tracing, software-based photon mapping is still computationally prohibitive for dynamic, interactive virtual environment and game applications. However, a “compute bound” GPU implementation whose performance will continue to improve with improving GPU floating point operations was introduced in by Purcell et al. [56]. Although the GPU-based photon mapping has not been applied to acoustical modeling, sonel mapping is the application of the (original) photon mapping method to acoustical modeling and has led to great computational savings [57]. Future work can include further computational savings to sonel mapping by appropriately modifying and incorporating Purcell’s GPU-based solution.
3.1.3. Acoustical Occlusion and Diffraction Modeling
Diffraction can be defined as the “bending mode” of sound propagation whereby sound waves go around an obstacle that lies directly in the line of straight propagation allowing us to hear sounds around corners and around barriers [58]. Diffraction is dependent on both wavelength and obstacle/surface size, increasing as the ratio between wavelength and obstacle size is increased [58]. The frequency spectrum of audible sound ranges from approximately 20 to 20 kHz, corresponding to wavelengths ranging from 17 to 0.02 m (with a velocity of vc = 343 m·s−1 for sound in air and a frequency of f Hz, wavelength λ = vc× f [58]). Since the dimensions of many of the objects/surfaces encountered in our daily lives is within the same order of magnitude as the wavelength of audible sounds, diffraction is an elementary means of sound propagation, especially when there is no direct path between the sound source and the receiver, such as in buildings [59] (see Fig. 4 for a graphical example). Despite the importance of diffraction, modeling occlusion/diffraction effects is a difficult and computationally intensive task (using traditional software-based methods) and as a result, typically ignored in virtual audio applications including games and virtual environments. However, the use of GPU for modeling occlusion/diffraction effects shows promise.
for a graphical example). Despite the importance of diffraction, modeling occlusion/diffraction effects is a difficult and computationally intensive task (using traditional software-based methods) and as a result, typically ignored in virtual audio applications including games and virtual environments. However, the use of GPU for modeling occlusion/diffraction effects shows promise.
Tsingos and Gascuel developed an occlusion and diffraction method that utilizes computer graphics hardware to perform fast sound visibility calculations that can account for specular reflections (diffuse reflections were not considered), absorption, and diffraction caused by partial occluders [60]. Specular reflections are handled using an image source approach [61] while diffraction is approximated by computing the fraction of sound that is blocked by obstacles in the path from the sound source to the receiver by considering the amount of volume of the first Fresnel ellipsoid that is blocked by the occluders. A visibility factor is computed using computer graphics hardware. A rendering of all occluders from the receiver’s position is performed and a count of all pixels not in the background is taken (pixels that are “set” i.e., are not in the background, correspond to occluders). Their approach handles a discrete set of frequency bands ranging from 31 to 8 kHz and is primarily focused on sounds for animations. Although experimental results are not extensive, their approach is capable of computing a frequency dependent visibility factor that takes advantage of graphics hardware to perform this in an efficient manner. Although their approach is not completely real-time, it is “capable of achieving interactive computation rates for fully dynamic complex environments” [60].
Tsingos and Gascuel later introduced another occlusion and diffraction method based on the Fresnel-Kirchoff optics-based diffraction approximation [59, 62]. The Fresnel-Kirchoff approximation is based on Huygens’ principle [63]. The total unoccluded sound pressure level at some point p in space is determined by calculating the sound pressure of a small differential area dS and integrating over the closed surface enclosing p (see Tsingos and Gascuel for further details regarding this calculation in addition to an algorithm outlining the method [62]). After determining the total unoccluded sound pressure arriving at point p from a sound source, diffraction and occlusion effects are accounted for by computing an occlusion depth-map of the environment between the sound source and the receiver (listener) using computer graphics hardware to permit real-time operation. Once the depth-map has been computed, the depth of any occluders between the sound source and the receiver can be obtained from the Z-buffer [64] whereby “lit” pixels correspond to occluded areas. The diffraction integral described by the Fresnel-Kirchoff approximation is then approximated as a discrete sum of differential terms for every occluded pixel in the Z-buffer. Given the use of graphics hardware, their method is well suited to the interactive auralization of diffracted energy maps [62]. Comparisons for several configurations with obstacles of infinite extent between their method and between boundary element methods (BEMs), gives “satisfactory quantitative results” [62].
Gallos and Tsingos [65] aim to improve audio rendering for virtual environments where sound propagation and sound blocking by numerous occluders should be accounted for. This problem is suitable for GPU implementation because it requires a large number of geometric calculations that can be computed in parallel and uses multiply-add (MADD) instructions. In this work, two common algorithms are implemented. Variable delay line is used to simulate the propagation time of an audio signal and is implemented using texture resampling. The filtering algorithm is used to simulate directivity, occlusion, and interaction with a medium and is implemented using a four component dot product function. Sound signals are stored as RGBA textures where each of the components holds a band pass copy of the original signal. Experimental results with a Pentium IV 3.0 GHz and an NVIDIA GeForce FX 5950 graphics card showed that the GPU performed 20% slower than the CPU. The authors suggest that the main bottleneck of the system is the lack of efficient floating-point texture support and that the performance of the GPU would improve by 50% if this issue is resolved. They also suggest a better use of pixel throughput and texture addressing as ways to improve the performance. This problem may be overcome using a newer video card such as the NVIDIA GTX 280 which supports double precision floating point numbers.
Cowan and Kapralos [66] introduced a GPU-based occlusion method capable of approximating plausible acoustical occlusion/diffraction. Experimental results of several simulations indicate that the method conforms to theoretical sound propagation and diffraction models which state that diffraction effects increase as obstacle size decreases and/or frequency decreases. Furthermore, the method is computationally efficient allowing for occlusion effects to be modeled in real-time for use in interactive and dynamic virtual environment and game applications.
4. SUMMARY
This paper has provided a summary of the GPU-based spatial sound techniques that can provide spatial sound for dynamic and interactive virtual environments and games. The methods and techniques described here are the outcome of a great interest in the possibility of utilizing graphics hardware technology for efficient implementation of complex and costly software-based spatial sound algorithms that currently cannot provide real-time performance except for trivial environments that are of limited use. Despite the computational speed-ups afforded by GPUs, they are currently far from perfect. A major bottleneck in GPU performance is the slow data transfer between the GPU and the CPU. The current accelerated graphics port (AGP) bus is not capable of handling the large amount of data transfers many of the proposed techniques require. In much of the work described here, slow bus traffic is explicitly identified as a performance bottleneck. Many researchers have expressed hope that with the arrival of the upcoming peripheral component interconnect (PCI)-express bus the situation would improve significantly. Also, one of the design goals behind Intel’s new Larrabee chip is to minimize communication between units by having a single multicore hybrid unit [67]. Furthermore, the limited programmability of GPUs has been a major obstacle in the way of general application development for this technology. While previous GPGPU research has resulted in an accumulated body of knowledge that is of immense help to developers, GPU programming is not yet as accessible as many developers might wish for. To overcome this problem, new programming capabilities are added with each new generation of GPU technology. One approach is to develop high level programming environments such as Microsoft’s high-level shading language (HLSL), the OpenGL shading language, and NVIDIA’s compute unified device architecture (CUDA) that add some CPU functionality to GPU architecture. Another approach, on which Intel’s upcoming Larrabee chip is based, is to combine the functions of the CPU and the GPU in a hybrid multicore general-purpose GPU design which can be programmed in the familiar x86 environment. These two approaches are very different. But regardless of which one will become dominant in the future, it seems that GPUs or other new parallel processing units will become easier to program for general applications. This will provide developers of audio applications for virtual environments and games with a host of exciting possibilities and opportunities.
Even with the tremendous computational performance improvements afforded by GPUs, considerable research and development remains to be done to facilitate the generation of convincing virtual sound for use in interactive virtual environments and games. The large computational requirements for physically accurate real-time acoustical modeling for complex, dynamic environments is still out of reach even with the latest GPUs. That being said, completely and faithfully recreating the acoustics of a particular environment may not be necessary; hearing is a perceptual process and there is no one-to-one mapping between physical acoustical phenomena and our perception of these phenomena. Therefore, accuracy may not always be necessary. Greater work needs to be done to take advantage of the human auditory perception system thus avoiding computations that have minimal (if any), perceptual consequences. A large problem of spatial sound generation is the customization of the HRTF for specific individuals [68]. Although preliminary, some work has investigated the use of individualized HRTF customization by modeling the interaction of sound with a model of the individual’s pinnae [42]. Accurately tracing sound through an accurate ear model is still computationally expensive for real-time applications (see [69] for some work in this area) but as GPU technology improves, perhaps such an approach may prove to be more feasible. Although not specific to auralization, the generation of “contact sounds”, sounds that correspond to the complex contact interactions between animated objects, is another open problem [70]. This is yet another area that stands for improvement with the improving GPU technology.
Finally, hardware technology is evolving at a tremendous pace and the success of GPU technology might motivate the design and production of other dedicated hardware solutions whose specialized design might later be exploited for solving these relevant problems. The widespread use of an analogous audio processing unit, with specialized computational power, may ultimately pave the way for innovative audio applications that can change our experience of computer usage in unforeseen ways.
ACKNOWLEDGMENTS
The financial support of the Natural Sciences and Engineering Research Council of Canada (NSERC) in the form of a Discovery Grant to Bill Kapralos and is gratefully acknowledged.

