- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

Open Economics and Management Journal
(Discontinued)
ISSN: 2352-6300 ― Volume 2, 2017
The Determinants of US Stock Market Returns
Samih A. Azar*
Abstract
In the literature there are many determinants for the times series of US stock returns. The most notable are: inflation, inflation uncertainty, and the relative change in the value of the US dollar. This paper aims to reconsider and update this research question. Monthly data sets are used with the S&P 500 as the measure of the stock market index, and the US trade-weighted foreign exchange rate index as the measure of the US dollar. Least squares regressions, GARCH regressions and least square regressions with endogenous calendar breakpoints are estimated. The evidence is strong that US inflation and US inflation uncertainty do not have an impact on US stock market returns. However, for the recent sample, a significant relation between the US S&P 500 and the US dollar exists, while in the older sample such a relation is negated. Finally, there is evidence that the growth rate in the money supply has a negative and delayed impact on US stock returns whatever the econometric specification. This anomalous relation runs against market efficiency.
Article Information
Identifiers and Pagination:
Year: 2014Volume: 1
First Page: 1
Last Page: 13
Publisher Id: EMJ-1-1
DOI: 10.2174/2352630001401010001
Article History:
Received Date: 11/2/2014Revision Received Date: 3/4/2014
Acceptance Date: 26/5/2014
Electronic publication date: 30/7/2014
Collection year: 2014
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution Non-Commercial License (http://creativecommons.org/licenses/by-nc/3.0/) which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
* Address correspondence to this author at the Faculty of Business Administration & Economics, Haigazian University, Mexique Street, Kantari, Beirut, Lebanon; Tel/Fax: +9611349230. E-mail: samih.azar@haigazian.edu.lb
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 11-2-2014 |
Original Manuscript | The Determinants of US Stock Market Returns | |
INTRODUCTION
There are three recognized determinants of stock market returns in the literature. The first determinant is inflation, the second one is inflation uncertainty, and the last one is the foreign exchange rate. Empirically, stock returns are negatively related to actual inflation, and to expected and unexpected inflation. Nonetheless more recent theoretical and empirical evidence challenges the existence of such a negative relation, and considers this relation to be non-fundamental once a “fundamental” variable is included in the regressions [1Azar SA. Inflation and stock returns Int J Acc Fin 2010; 2 (3/4): 254-74.]. This fundamental variable is derived from the Gordon constant growth dividend model, and is the change in the cost of equity.
Theoretically, there is a claim that higher inflation is caused by higher inflation uncertainty, with the direction of causality going from inflation uncertainty to inflation. Thus the assumed negative relation is between inflation uncertainty, and not inflation, and stock returns. This is due, first, to the fact that higher inflation uncertainty increases the required risk premium, leads to a higher discount rate, and lowers the discounted present value of expected future cash flows, thus resulting in a fall in stock prices. Second, economic activity is adversely affected by inflation uncertainty and, since stock returns lead economic activity, there is a negative relation between stock returns and inflation uncertainty.
Empirically there is evidence that inflation uncertainty explains stock returns better than inflation but with the same negative impact. See the survey in [2Azar SA. The spurious relation between inflation uncertainty and stock returns: Evidence from the U.S Rev Eco Fin 2013; 3(4): 99-109.]. However, [2Azar SA. The spurious relation between inflation uncertainty and stock returns: Evidence from the U.S Rev Eco Fin 2013; 3(4): 99-109.] presents strong evidence that inflation uncertainty also fails to explain stock returns when the same “fundamental” variable is included in the regressions, although the effect of inflation uncertainty dominates the effect of inflation on stock returns.
The rationale for the irrelevance of inflation and inflation uncertainty comes about from the following. Since higher inflation occurs with higher inflation uncertainty, inflation uncertainty increases the risk premium in the discount rate but, at the same time, expected future cash flows are higher because of more inflation, leading to no change in the present value of these expected future cash flows, and consequently stock prices remain unchanged, and stock returns are not affected.
The third relation is between US stock prices and the US dollar. There are two theoretical justifications for a link between stock markets and the foreign exchange rate. The first approach is concerned about the current account of the balance of payments [3Dornbusch R, Fischer S. Exchange rates and the current account Ame Eco Rev 1980; 70: 960-71.]. A depreciation of the foreign exchange rate makes export-oriented firms more competitive and they generate more profits from international trade. Since stock prices are equal to discounted future cash flows, and since higher earnings mean higher cash flows, then stock prices are positively impacted. Nonetheless such a relation breaks down, and changes sign, if firms are import-oriented, relying on foreign inputs into their production process. In such a case a depreciation of the foreign exchange rate raises the cost of inputs and compresses profits, lowering stock prices. In both cases the causality runs from the foreign exchange rate to the stock market.
The second approach is oftentimes named the portfolio balance theory [4Frankel J. Monetary and portfolio balance models of exchange rate determination In: Bhandari JS, Putman BH, Eds. Economic interdependence and flexible exchange rates. MIT: Cambridge 1983; pp. 84-115.]. If stock prices are higher this makes people wealthier. Higher wealth increases the domestic and foreign demand for the US dollar which thereby appreciates. Higher wealth increases also the domestic demand for money, raising interest rates and attracting more foreign capital and, consequently, the US dollar again appreciates. Of course this assumes that central banks do not react by countering the rise in interest rates. However, there is an inherent problem with such a transmission channel. The change in stock prices is considered exogenous. There is a need to know which factor has caused the change in stock prices. If the change comes from higher earnings then this second approach becomes similar to the first approach whereby product exports or imports of inputs affect earnings, and therefore stock prices.
The empirical evidence on a link between stock prices and foreign exchange rates is mixed. In general the link is significant in developing countries but not in developed ones. For the latter the link may depend on the period considered in the analysis, on whether the economy is in a recession or not, or if calendar breakpoints, or more than one regime, are allowed for. See the surveys in [5Azar SA. US stocks and the US dollar Int J Fin Res 2013; 4(4): 91-106., 6Azar SA. US stocks and the US dollar II Int Res J Fin Eco 2013; (117): 188-216.].
The paper is organized as follows. The second section provides for the theoretical methodology. Section 3 gives the source of the data. Sections 4, 5, 6 and 7 are the empirical parts. Section 4 studies the impact of lagged money supply growth rates on US stock returns. The following two sections, sections 5 and 6, test respectively for the statistical significance and relevance of inflation and of inflation uncertainty in stock return regressions. Including in the regressions either inflation or inflation uncertainty does not produce any statistically significant relation with the US S&P 500 log return once other fundamental variables are also included. This conforms to [1Azar SA. Inflation and stock returns Int J Acc Fin 2010; 2 (3/4): 254-74., 2Azar SA. The spurious relation between inflation uncertainty and stock returns: Evidence from the U.S Rev Eco Fin 2013; 3(4): 99-109., 7Azar S A. Inflation and stock returns II Int J Eco Fin 2014; 6(1): 208-16.]. In section 7 the relevance for stock returns of the relative change in a dollar index is tested. The latter is found to be a significant explanatory variable during the more recent period. This contradicts [5Azar SA. US stocks and the US dollar Int J Fin Res 2013; 4(4): 91-106.] but confirms [6Azar SA. US stocks and the US dollar II Int Res J Fin Eco 2013; (117): 188-216., 8Azar SA. The US Dow and the US dollar App Eco Let 2014; 21(10): 683-.
[http://dx.doi.org/10.1080/13504851.2014.884690] ]. Section 8 dwells on the evidence from the interest rate markets. The final section concludes.
THE MODEL
The model in this paper borrows from a relation developed by Williams [9Williams JB. The theory of investment value. Cambridge: Harvard University Press 1938.], Gordon and Shapiro [10Gordon MJ, Shapiro L. Capital equipment analysis: The required rate of profit Manage Sci 1956; 3(1): 102-.
[http://dx.doi.org/10.1287/mnsc.3.1.102] ], and Gordon [11Gordon M. Dividends, earnings and stock prices Rev Eco Stats 1959; 41(2): 99-105.
[http://dx.doi.org/10.2307/1927792] , 12Gordon M. The investment, financing, and valuation of the corporation Homewood Irwin 1962.] and which is:
(1)
where P is the stock price, D is the real dividend, E is after-tax real earnings, π is the constant payout ratio, k is the cost of equity, g is the constant growth rate in dividends, and measures also the capital gain’s yield, and t is the time period. Taking a Taylor series expansion of equation (1), with higher order terms omitted, one finds:
(2)
Dividing both sides of equation (2) by P one obtains:
(3)
Equation (3) identifies three fundamental variables that explain the relative change in stock prices. The first is the periodic rate of change in the stock price, the second is the change in k, and the third is the relative change in real earnings E. The first variable should produce a coefficient equal to the average drift in stock prices. The second variable should produce a coefficient equal to the negative of the inverse of the dividend yield. And the third variable should produce a coefficient that has a unitary coefficient. Equation (3) summarizes all theoretical factors that explain the relative price change of a stock.
The effect of inflation and inflation uncertainty on stock prices work through the nominal cost of equity k, and through the constant dividend growth rate g. Since inflation and inflation uncertainty are positively correlated, both increase the nominal k and the nominal g, keeping the difference (k-g) constant. The effect of the foreign exchange rate comes about from the indirect effect of this rate on real earnings E. Total earnings E are now the sum of domestic earnings Ed and foreign earnings Ef. Let it be assumed that Ed = k E, and that Ef =(1-k)E, with 0 <k <1. If X denotes the foreign exchange rate, whereby an increase in X is a depreciation of the US dollar, then it is reasonable to state that the following relations exist [13Levi MD. International finance: The markets and financial management of multinational business. New York: McGraw-Hill 1990.], with A being a positive constant, and q being the volume of trade in units, such as either exports or imports depending on the case:
(4)
In equation (4) θ is a constant that can be either positive and higher than +1 if the firm is export-oriented, or negative if the firm is import-oriented, or it may be statistically insignificant if both transmission channels work together. Replacing E in equation (1) by Ed + Ef, using the relations between Ed and Ef with E, using the term to the left of equations (4) for Ef, and noting that the average drift μ = (∂(P)/P∂(t))d(t) for d(t), i.e. one month, since the data is monthly, the following model can be derived:
(5)
Equation (5) is in continuous time. The discrete time version is:
(6)
where log is the natural logarithm, Δ is the first-difference operator, μ, β, γ and λ are the regression constants, and ε is the regression residual. Equation (6) is a relation between the change in the natural logs of a stock price and three independent variables. The first is the change in k, with the proportionality factor being equal to the negative inverse of the dividend yield, (k − g) = Dt+1 / Pt, which happens to be also the (modified) duration of the stock [14Hallerbach WG. Cross-and auto-correlation effects arising from averaging the case of US interest rates and equity duration App Fin Eco 2003; 13(4): 287-94.
[http://dx.doi.org/10.1080/09603100210135720] , 15Baz J, Chacko G. Financial derivatives, pricing, applications, and mathematics. Cambridge: Cambridge University Press 2004.
[http://dx.doi.org/10.1017/CBO9780511806643] ]. The second variable is the relative change in domestic real earnings whose coefficient measures the share of domestic income out of total income. And the third variable is the relative change in the foreign exchange rate, whose coefficient measures the economic exposure of the typical firm. The constant or intercept should indicate the average (monthly) drift. Equation (6) is the equation of what is here called the fundamentals. It does not include any other additional variable. Most particularly it does not include explicitly either inflation or inflation uncertainty.
DATA SOURCE
The data series for the US monthly S&P 500, the monthly US baa corporate bond yield, the monthly MZM money supply, the monthly consumer price index (CPI, all items), the monthly real personal disposable income, and the monthly trade-weighted US dollar index, are all retrieved from the web site of the Federal Reserve Bank of Saint Louis. An increase in the US dollar index is an appreciation of the US dollar. The first differences of the natural logs of the S&P 500, of the CPI, of the MZM money supply, of the real personal disposable income, and of the US dollar are all calculated. These 5 differenced variables are all stationary in distribution when the Phillips and Perron unit root test [16Phillips PCB, Perron P. Testing for a unit root in time series regression Biometrica 1988; 75 (2): 335-46.
[http://dx.doi.org/10.1093/biomet/75.2.335] ], with a constant and a trend, is applied to them. The actual p-values for the null hypotheses of a unit root are all less than 0.0001. The change in the baa corporate bond yield, divided by 1200 to get monthly decimal figures, is utilized in the regressions. This differenced variable is found to be stationary in distribution when the same unit root test as before is applied to it, with an actual p-value less than 0.0001 under the null of a unit root. This variable stands as a proxy for Δ (k). This choice is dictated by the observation that the baa corporate bond yield carries substantial default risk and its variation should be close to that of the cost of equity. Even if there is an inherent measurement error with such a proxy to the cost of equity the econometric problem that arises seems to be light [1Azar SA. Inflation and stock returns Int J Acc Fin 2010; 2 (3/4): 254-74.]. The continuously compounded real personal disposable income stands as a proxy for the relative change in real earnings. In [2Azar SA. The spurious relation between inflation uncertainty and stock returns: Evidence from the U.S Rev Eco Fin 2013; 3(4): 99-109.] the industrial production index replaces real personal disposable income as the measure of stock earnings.
THE DELAYED EFFECT OF MONEY GROWTH RATES
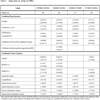
The regression in equation (6) is first estimated without the log return of the US dollar index, but including lagged values of the growth rate in the MZM money supply (Table 1). The rationale is that money supply may affect stock prices with “long and variables lags,” although an immediate impact is more reasonable if market efficiency is to hold. Moreover market efficiency implies also that share prices react to changes in expectations about money supply well before the actual change happens. Hence the finding of a delayed effect is extremely anomalous. Nonetheless intellectual honesty binds the author of this paper to report the results as they are. Moreover, the other regression results are little affected by the inclusion of this delayed effect, and this effect remains significant in all the different specifications that are carried out. For all these reasons it was decided to keep the lagged variables in the estimated models.
All computations are carried out with the statistical software EViews 8 [17EViews 8 In: Irvine. CA: IHS Global Inc 2013.]. The second column of Table 1 includes the eleventh lagged value of the growth rate of the money supply. The third column in the same table includes the twelfth lag of that same variable. The fourth column includes the thirteenth lag. The fifth column includes all 3 lags together, and the last column includes the average of the three lagged growth rates. All regressions include a GARCH(1,1) specification of the conditional variance of the residuals. In all five specifications the coefficients in the conditional variance equations are all statistically significantly different from zero.
The impact of the change in the proxy for the cost of equity is highly significant statistically with absolute t-statistics ranging between 5.956396 and 6.071149. The coefficients on this proxy vary closely between -58.05973 and -58.46895. The absolute values of these coefficients are estimates of the (modified) duration. Hence the duration is between 58.05973 and 58.46895 years. The specification in column 6 of Table 1 gives an estimated duration of 58.43239 years.
The impact of the log change in real personal disposable income is also statistically significant. The t-statistics range between 2.526202 and 2.665431. The estimates of the impact vary between 0.489331 and 0.516063. The specification in column 6 of Table 1 gives an estimate of the impact of 0.514542, an impact which is statistically significantly different from +1 with an absolute t-statistic of 2.50758. Hence real stock earnings do not move proportionately with real personal disposable income and this is as expected theoretically from the fact that 0 <κ <1 in equation (5).
The regression results in Table 1 show that the three lagged values of the growth rate of the money supply have statistically significant impacts on the log returns of the S&P 500. It seems that it takes between 11 and 13 months for the effect of the money supply to be felt in stock prices. The absolute t-statistics are 2.709045 for the eleventh lag, 2.891382 for the twelfth lag, and 2.788022 for the thirteenth lag. When all three lags are included (5th column of Table 1) they are individually insignificant statistically with the lowest p-value being 0.1752. However, a Wald test that the three coefficients on the lagged growth rates are jointly zero rejects this null hypothesis with an actual p-value of 0.0044. In addition the log likelihood ratio test for the same hypothesis has a p-value of 0.0031. Therefore the three coefficients are not jointly statistically insignificant. The last specification in column 6 of Table 1, in which is included the average of the three lagged growth rates of the money supply, is selected to be the best one by all three information criteria, the Akaike, Schwarz, and Hannan-Quinn criteria. That is why this specification is chosen in subsequent analysis. The average lagged money growth rate has an impact of -0.870091 with an absolute t-statistic of 3.546191. The impact is statistically insignificantly different from -1 with a t-statistic of 0.529462. However the fact that this impact is delayed and negative, and statistically significantly so, is very puzzling because the theoretical expectations are that money supply should have a positive and immediate impact on stock prices.
Finally, the estimate of the yearly average equity return, obtained from the intercept of the last specification in column 6 of Table 1, is 11.3905%. This estimate compares with an estimate of 11.3% in Brealey et al. [18Brealey RA, Myers SC, Allen F. Principles of corporate finance In: Global edition. 11th. New York: McGraw-Hill 2014.]. Hence the model provides for reasonable estimates, implying that the underlying specification is deemed appropriate.
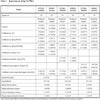
THE IRRELEVANCE OF INFLATION
First the same unit root test as before is conducted on the inflation variable. The null hypothesis of a unit root is easily rejected at a marginal significance level less than 0.0001. Column 2 of Table 2 presents the econometric results of the regression that includes this continuously compounded inflation rate, in addition to the proxy for the change in the cost of equity, to the proxy for the relative change in real earnings, and to the delayed money supply average growth rate. Applying the Pai-Perron test [19Bai J. Estimating multiple breaks one at a time Econ Theory 1997; 13: 315-52.
[http://dx.doi.org/10.1017/S0266466600005831] , 20Bai J, Perron P. Estimating and testing linear models with multiple structural changes Econometrica 1998; 66: 47-78.
[http://dx.doi.org/10.2307/2998540] ] for an endogenous calendar breakpoint finds no breaks. All coefficients have the correct sign and statistical significance except the coefficient on the inflation rate which is statistically insignificantly different from zero with an absolute t-statistic of 0.487215.
Column 3 of Table 2 adds to the above regression a GARCH(1,1) specification of the conditional variance. Again all coefficients have the correct sign and statistical significance except the coefficient on the inflation rate which is statistically insignificantly different from zero with an absolute t-statistic of 0.219542.
Inflation is then modeled as an ARIMA(0,1,1) process and the fitted values and the residuals are generated. Including these two variables, in place of the actual inflation rate, provides the results in column 4 of Table 2. All coefficients have the correct sign and statistical significance except the two coefficients on the predicted inflation rate and on the innovations in the inflation rate, which are statistically insignificantly different from zero with absolute t-statistics of 1.197264 and 1.415218 respectively. Applying a Wald test under the null that both these two coefficients are jointly zero gives an actual p-value of 0.3653, failing to reject the null hypothesis.
In column 5 of Table 2 a GARCH(1,1) model of the conditional variance is added to the model in the previous paragraph. All coefficients have the correct sign and statistical significance except the two coefficients on the predicted inflation rate and on the innovations in the inflation rate, which are statistically insignificantly different from zero with absolute t-statistics of 1.010066 and 0.955703 respectively. Applying a Wald test under the null that both these two coefficients are jointly zero gives an actual p-value of 0.5539, failing to reject the null hypothesis.
Finally, the absolute residuals are added to the model in the previous paragraph to test for a possible differential effect of positive and negative inflation errors. All coefficients have the correct sign and statistical significance except the three coefficients on the predicted inflation rate, the innovations in the inflation rate, and the absolute values of these innovations, which are statistically insignificantly different from zero with absolute t-statistics of 1.025360, 0.951314, and 0.166536 respectively. Applying a Wald test under the null that all these three coefficients are jointly zero gives an actual p-value of 0.7556, failing to reject the null hypothesis.
All these results point to the same fact. Inflation does not enter significantly in regressions that explain stock returns once fundamental variables are included in these regressions. This is true when inflation is taken as it is, when inflation is separated into its predicted and unpredicted components, and when the unpredicted component is separated into positive and negative values. The negative relations in the literature are simply due to the misspecification of the econometric model. Moreover, the three information criteria, Akaike, Schwarz, and Hannan-Quinn, select the model in Table 1, column 6, over all five models in Table 2. Notably the model in Table 1, column 6, includes none of the inflation-related variables.
The coefficients on the other variables in the regressions of Table 2 have signs and magnitudes that are comparable to the estimates in Table 1. The stock durations range between 50.99889 years and 57.93669 years and their t-statistics are between 4.301666 and 6.006794. The coefficients on the relative change in real personal disposable income range between 0.495110 and 0.617094 with t-statistics that are between 2.564089 and 3.042664. And the coefficients on the average lagged money growth rates range between -0.766744 and -0.870243 with absolute t-statistics that are between 2.921106 and 3.545438. The intercepts imply average annual equity returns between 11.847% and 14.319%, estimates which are rather on the high side.
THE IRRELEVANCE OF INFLATION UNCERTAI-NTY
As in [2Azar SA. The spurious relation between inflation uncertainty and stock returns: Evidence from the U.S Rev Eco Fin 2013; 3(4): 99-109.], inflation uncertainty is measured by two proxies: the absolute value of the inflation rate and the square of the inflation rate. The rationale behind such assumptions is also found in [2Azar SA. The spurious relation between inflation uncertainty and stock returns: Evidence from the U.S Rev Eco Fin 2013; 3(4): 99-109.]. Other proxies for inflation uncertainty have their own drawbacks. Unit root tests, as has been done previously, are applied to these two variables. The two null hypotheses of a unit root are easily rejected at marginal significance levels less than 0.0001. Hence these two proxies for inflation uncertainty are stationary in distribution. Table 3 presents the empirical results that include these two proxies in addition to the other three variables: the proxy for the change in the cost of equity, the proxy for the relative change in real earnings and the delayed impact of the average money growth rate.
Column 2 of Table 3 selects the absolute value of inflation and adds a GARCH(1,1) model of the conditional variance. All coefficients have the correct sign and statistical significance except the coefficient on the absolute value of the inflation rate, which is statistically insignificantly different from zero with a t-statistic of 0.043652. Column 3 of Table 3 selects the square of inflation and adds a GARCH(1,1) model of the conditional variance. All coefficients have the correct sign and statistical significance except the coefficient on the square of the inflation rate, which is statistically insignificantly different from zero with an absolute t-statistic of 0.018718. No calendar breakpoints are selected for the regression with the absolute value of the inflation rate. And the latter variable has a coefficient which
is still statistically insignificantly different from zero with an absolute t-statistic of 0.301779 (column 4 of Table 3).
However when the Bai-Perron test for a calendar breakpoint is applied to the regression with the square of inflation as the measure of inflation uncertainty, a breakpoint is selected on October 1974. In the ancient sample (1960M03-1974M09) the square of inflation has a statistically significant coefficient with an absolute t-statistic of 3.076655, while the average growth rate of the money supply does not carry a significant coefficient (t-statistic: 0.928118). In the more recent sample (1974M10-2013M11) the square of inflation has an insignificant coefficient, but all other coefficients have the expected signs and statistical significance. If the regression of the distant sample is estimated separately and without the average money growth variable, the coefficient on the square of inflation is still statistically significant (absolute t-statistic: 2.483767), but less so than previously. As argued in [7Azar S A. Inflation and stock returns II Int J Eco Fin 2014; 6(1): 208-16.] this is due to the non-stationarity of the underlying variable. An augmented Dickey-Fuller test [21Dickey DA, Fuller WA. Distribution of the estimators for autoregressive time series with a unit root J Ame Stat Ass 1979; 4 (366): 427-31.], with a constant but without a trend, produces a p-value of 0.9975, and the same test with a trend produces a p-value of 0.9982. Hence the null of non-stationarity is not rejected. This implies that the distribution of the coefficient on the square of inflation follows a non-standard distribution that lies in between a normal distribution and a Dickey-Fuller distribution. The critical values of the Dickey-Fuller distribution, with a constant but without a trend, are -2.575737 (10%), -2.878212 (5%), and -3.468521 (1%). The figures in parenthesis are upper-tailed marginal significance levels. Comparing these critical values to the actual t-statistic of -2.483767 shows clearly that the latter t-statistic falls in the region of statistical insignificance under a Dickey-Fuller distribution, with a two-tailed marginal p-value higher than 20%.
The above results have provided strong evidence that, not only is inflation irrelevant, but inflation uncertainty is also irrelevant in stock regressions that include other fundamental variables. Hence neither inflation nor inflation uncertainty explains significantly stock returns. The reason for such a result is that higher inflation increases both the nominal cash flows and the discount rate, leaving stock prices unchanged. Since inflation and inflation uncertainty are positively correlated an increase in inflation uncertainty produces the same result as that of inflation, meaning that stock prices and stock returns remain unaffected.
The coefficients on the other variables in the regressions in Table 3 have the correct and the same signs as those in Tables 1 and 2. However the magnitudes of these coefficients are more variable, although their high statistical significance is not affected.
In parts of the literature inflation uncertainty is measured by a GARCH process [22Hu X, Willett TD. The variability of inflation and real stock returns App Fin Eco 2000; 10 (6): 655-.
[http://dx.doi.org/10.1080/096031000438006] , 23Lin SC. Inflation and real stock returns revisited Eco Inq 2009; 47 (4): 783-95.]. An EGARCH model [24Nelson DB. Conditional heteroskedasticity in asset returns: a new approach Economterica 1991; 59: 347-70.
[http://dx.doi.org/10.2307/2938260] ] for the conditional variance of inflation is estimated. The conditional mean equation includes six lagged values of the inflation rate that all turn out to have statistically significant coefficients. The logs of the fitted GARCH volatilities are included in the regressions on the log return of the S&P 500 together with the proxy for the cost of equity, and to the continuously compounded growth rate in real disposable income. The delayed effect of the money supply growth rates is included in an additional regression. Table 4 reproduces the results. The coefficients on the logged GARCH variable are statistically insignificant whatever the model and whatever the sample sub-period. For example when the lagged money growth rates are excluded from the regression the t-statistic on the logged GARCH variable is 0.2618, while the t-statistic is 0.0580 when the lagged money growth rates are included. In addition in breaking the sample into two sub-periods the t-statistic on the logged GARCH variable is 1.6405 in the older sample and in the recent sample it is 0.7625. Therefore the evidence is strong that a GARCH estimate of the inflation uncertainty provides statistically insignificant results exactly like when other proxy measures of inflation uncertainty are used.
THE EFFECT OF THE US DOLLAR (ECONOMIC EXPOSURE)
In this section regression equation (6) is estimated as it is, and includes the relative change in the trade-weighted US dollar index. Inflation, absolute inflation, and the square of inflation are added separately as variables together with the other two fundamental variables and the delayed effect of the average money growth rate. Table 5 presents the empirical results. All regressions are modeled with a GARCH(1,1) process of the conditional variance. In the regression presented in column 2 of Table 5, the null hypothesis that the two coefficients on the log return of the US dollar and on the inflation rate are both statistically insignificantly different from zero fails to be rejected with an actual p-value of 0.4782. All other coefficients are statistically significant except for the coefficient on the relative change of real personal disposable income which is only marginally significant (t-statistic: 1.9300). In the regression presented in column 3 of Table 5, the null hypothesis that the two coefficients on the log return of the US dollar and on the absolute inflation rate are both statistically insignificantly different from zero fails to be rejected with an actual p-value of 0.4857. All other coefficients are statistically significant except for the coefficient on the relative change of real personal disposable income which is only marginally significant (t-statistic: 1.9356). In the regression presented in column 4 of Table 5, the null hypothesis that the two coefficients on the log return of the US dollar and on the square of the inflation rate are both statistically insignificantly different from zero fails to be rejected with an actual p-value of 0.4924. All other coefficients are statistically significant, except for the coefficient on the relative change of real personal disposable income which is only marginally significant (t-statistic: 1.9424). Notably, the three coefficients in the three above regressions on the average lagged money growth rates are statistically highly significant with actual absolute t-statistics of 3.583844, 3.583266, and 3.608742 respectively.
Table 6 presents additional econometric results for the regression equation (6), which includes again the relative change in the trade-weighted US dollar index. Inflation, absolute inflation, and the square of inflation are also added separately as variables, as well as the other three variables identified above. However, the statistical procedure that is implemented in Table 6 is the Bai-Perron least squares with a calendar breakpoint, but without a model of the conditional variance. The three regressions have a breakpoint on July 1998, which is the same breakpoint as in [6Azar SA. US stocks and the US dollar II Int Res J Fin Eco 2013; (117): 188-216.]. What is noteworthy is that, in the three models, the sample before the breakpoint produces statistically insignificant coefficients on the relative change in the US dollar, and on each one of the coefficients on inflation, absolute inflation, and the square of inflation. The actual p-values are respectively 0.6813, 0.7667, and 0.8330, and these fail to reject the three joint null hypotheses that the respective two coefficients are zero. All other coefficients are statistically significantly different from zero, including the coefficients on the relative change in real personal disposable income and on the average lagged money growth rate. However, in the recent samples, i.e. the samples from 1998M07 to 2013M11, the only significant coefficients are those on the log return of the US dollar index, with absolute t-statistics of 4.164494, 4.172982, and 4.134442. All the other coefficients are jointly insignificantly different from zero with respective actual p-values of 0.3251, 0.2929, and 0.3047. Therefore the evidence is strong that there is a calendar breakpoint that divides the sample into two different regimes. One of the regimes finds the relative change in the US dollar as the only insignificant variable, and the other regime finds this relative change as the only significant variable. These results corroborate those in [6Azar SA. US stocks and the US dollar II Int Res J Fin Eco 2013; (117): 188-216., 8Azar SA. The US Dow and the US dollar App Eco Let 2014; 21(10): 683-.
[http://dx.doi.org/10.1080/13504851.2014.884690] ]. In addition like in [6Azar SA. US stocks and the US dollar II Int Res J Fin Eco 2013; (117): 188-216., 8Azar SA. The US Dow and the US dollar App Eco Let 2014; 21(10): 683-.
[http://dx.doi.org/10.1080/13504851.2014.884690] ] a depreciation of the US dollar increases stock returns.
From Table 6 estimates of two theoretical parameters can be deduced. The first parameter is K, the share of domestic income out of total income (see equation (5)), and the estimates range from 56.0% to 57.2%, figures that do not seem to be out of place. See for example [25Grubert H. Foreign taxes and the growing share of U.S. multinational company income abroad: Profits, not sales, are being globalized Nat Tax 2012; 65(2): 247-82.]. The second parameter is θ, the foreign exchange rate elasticity of foreign income (see equations (4)), and the estimates range from 3.654 to 3.737, all being higher than +1 as expected. This means that a 1% depreciation of the US dollar leads to about a 3.7% rise in foreign-based income, or even in exports. Starting from equilibrium it can be demonstrated that:
(7)
The last term in equations (7) implies that the effect of the relative change of the foreign exchange rate on total income (1−κ )θ is nothing else but the coefficient of this relative change in the estimated regressions (see equation (5)). The estimates of this coefficient, obtained from Table 6, vary between -1.6009 and -1.6080, with a minimum absolute t-statistic of 4.1344. Therefore a 1% depreciation of the US dollar leads to around a 1.6% rise in total income and in stock returns. This dual effect, being statistically highly significant, adds to the evidence in [26Jorion P. The exchange-rate exposure of U.S. multinationals J Bus 1990; 63(3): 331-45.
[http://dx.doi.org/10.1086/296510] ], but runs counter the more recent evidence in [27Lee B-S, Suh J. Exchange rate changes and the operating performance of multinationals Euro Fin Manage 2012; 18(1): 88-116.
[http://dx.doi.org/10.1111/j.1468-036X.2009.00522.x] ]. Paradoxically, and although their evidence is weak, [28Muller A, Verschoor WFC. European foreign exchange risk exposure Euro Fin Manage 2006; 12(2): 195-220.
[http://dx.doi.org/10.1111/j.1354-7798.2006.00316.x] ] find that a depreciation of the euro has a negative, and not a positive, impact on European stock returns.
THE EVIDENCE FROM THE INTEREST RATE MARKETS
In this section related empirical evidence from the interest rate markets is surveyed. This is crucial because the empirical evidence in the bond market is at odds with that in the stock market, and sheds a new light on the estimated relations in this paper.
The fundamental theoretical starting point is the Fisher equation [29Fisher I. The theory of interest. New York: MacMillan 1930.]:
(8)
In equation (8) R stands for the nominal return on a financial asset, either a stock or a bond, πe is the expected, or ex ante, inflation rate, that is often approximated by the actual inflation rate, and re is the expected, or ex ante, real rate. The usual assumption is that the real ex ante return is constant, or at least stationary, which implies that the nominal return on the asset varies unit proportionally with expected inflation. As Campbell and Ammer [30Campbell J, Ammer J. What moves the stock and bond markets? A variance decomposition for long-term asset returns The J Fin 1993; 48(1): 3-37.
[http://dx.doi.org/10.1111/j.1540-6261.1993.tb04700.x] , p. 33Crowder WJ, Hoffman DL. The long-run relationship between nominal interest rates and inflation: The Fisher equation revisited J Money Credit Bank 1996; 28(1): 102-8.
[http://dx.doi.org/10.2307/2077969] ] write: “increases in long-run expected inflation tend to drive the stock market up and the bond market down.” In other terms expected inflation tends to increase bond yields and reduce stock returns, and therefore the Fisher equation tends to apply to bonds in the interest rate market but not to stocks in the stock market.
Mehra [31Mehra YP. Some key empirical determinants of short-term nominal interest rates Federal Res Bank Richmond Econ Quarterly 1995; 81(3): 33-51.] finds that anticipated inflation and the level of the interest rate are cointegrated, meaning that there is a long run relation between the two of them, with a cointegration coefficient equal to +1. However Kasibhatla [32Kasibhatla KM. The relation between inflation and interest rates: A cointegration analysis Int J Fin 2011; 23(4): 7034-44.] finds evidence for an “augmented Fisher effect” whereby the coefficient of proportionality is statistically significantly higher than +1. According to [33Crowder WJ, Hoffman DL. The long-run relationship between nominal interest rates and inflation: The Fisher equation revisited J Money Credit Bank 1996; 28(1): 102-8.
[http://dx.doi.org/10.2307/2077969] ], this feature is explained by taxation and hence it is necessary to compute the after-tax Fisher effect which [33Crowder WJ, Hoffman DL. The long-run relationship between nominal interest rates and inflation: The Fisher equation revisited J Money Credit Bank 1996; 28(1): 102-8.
[http://dx.doi.org/10.2307/2077969] ] find to be unitary. Barr and Pesaran [34Barr DG, Pesaran B. An assessment of the relative importance of
real interest rates, inflation, and term premiums in determining the
prices of real and nominal U.K. bonds Rev Eco Stat 1997; 79(3): 362-6.
[http://dx.doi.org/10.1162/003465300556931] ] study bonds in the U.K. market. They find a strong relation between unexpected movements in bond prices and revision of expectations to inflation. Bandholz et al. [35Bandholz H, Clostermann J, Seitz F. Explaining the US bond yield conundrum App Fin Eco 2009; 19: 539-0.
[http://dx.doi.org/10.1080/09603100801964370] ] test for a general interest rate model that includes the stance of monetary policy, the effect of business cycles, and the impact of inflation expectations. This is a model quite similar in structure to this paper’s model. If the short rate is included with the other three regressors, and under the pure expectations hypothesis of the term structure, the expected coefficient on the short rate should be +1, and that on the expected inflation rate should be zero. However [35Bandholz H, Clostermann J, Seitz F. Explaining the US bond yield conundrum App Fin Eco 2009; 19: 539-0.
[http://dx.doi.org/10.1080/09603100801964370] ] find that, in the long run, both coefficients are positive and statistically significant. Bae and Yi [36Bae SC, Yi TD. Structural breaks and the Fisher hypothesis in bond and stock markets App Fin Eco 2009; 19: 1961-73.
[http://dx.doi.org/10.1080/09603100903282614] ] study the bond and the stock market conjointly and test for the presence of structural breaks in the time series. They adopt two different methods for identifying the breaks which they express as a persistent supply shock to the firm’s production function, and thereby a persistent shock to the marginal return on capital, i.e. the real rate, making it a non-stationary variable. They present evidence that the negative relation between inflation and stock returns is limited to certain periods only. The same applies to the interest rate market. In brief, during the period after the first quarter of 1982, the Fisher hypothesis cannot be rejected in both markets. This means that stocks are a hedge to inflation and that their relation with inflation is positive and statistically insignificantly different from +1. This evidence runs contrary to the evidence in parts of the literature of a negative relation in the stock market. The existence of both a positive and a negative relation implies that the true relation may simply be insignificant as found in this paper. Most of the above authors [31Mehra YP. Some key empirical determinants of short-term nominal interest rates Federal Res Bank Richmond Econ Quarterly 1995; 81(3): 33-51.-33Crowder WJ, Hoffman DL. The long-run relationship between nominal interest rates and inflation: The Fisher equation revisited J Money Credit Bank 1996; 28(1): 102-8.
[http://dx.doi.org/10.2307/2077969] , 35Bandholz H, Clostermann J, Seitz F. Explaining the US bond yield conundrum App Fin Eco 2009; 19: 539-0.
[http://dx.doi.org/10.1080/09603100801964370] , 36Bae SC, Yi TD. Structural breaks and the Fisher hypothesis in bond and stock markets App Fin Eco 2009; 19: 1961-73.
[http://dx.doi.org/10.1080/09603100903282614] ] find expected inflation to possess a non-stationary distributional property in contrast to the evidence in this paper. The reason may lie in the sample period selected, in the data frequency utilized, and on the presence of any breaks. For example, Malliaropulos [37Malliaropulos D. A note on non-stationarity, structural breaks, and the Fisher effect J Bank Financ 2000; 24: 695-707.
[http://dx.doi.org/10.1016/S0378-4266(99)00064-3] ] finds a structural break in the data that, when accounted for, makes the relevant series stationary. Nonetheless he finds strong support for a Fisher effect between inflation and nominal interest rates both in the medium term and in the long run.
Cebula [38Cebula R. An empirical analysis of the impact of federal budget
deficits on long-term nominal interest rate yields, 1973.2-1995.4,
using alternative expected inflation measures Rev Fin Eco 1998; 7(1): 55-64.
[http://dx.doi.org/10.1016/S1058-3300(99)80145-1] , 39Cebula R. A contemporary investigation of causality between the primary government budget deficit and the ex ante real long term interest rate in the US Banca Nazionale Del Lavoro Quarterly Review 2002; 223: 417-35.] tests for the effect of US budget deficits on long term interest rates, whether nominal [38Cebula R. An empirical analysis of the impact of federal budget
deficits on long-term nominal interest rate yields, 1973.2-1995.4,
using alternative expected inflation measures Rev Fin Eco 1998; 7(1): 55-64.
[http://dx.doi.org/10.1016/S1058-3300(99)80145-1] ] or real [39Cebula R. A contemporary investigation of causality between the primary government budget deficit and the ex ante real long term interest rate in the US Banca Nazionale Del Lavoro Quarterly Review 2002; 223: 417-35.]. He uses corporate bond yields as a measure of the long-term interest rate. One variable that is included in the regressions is the lagged ratio of the money supply M2 over GDP. He finds that this lagged variable has a statistically significant and negative effect on interest rates.1 Since his data has a quarterly frequency the first lag of such a variable represents a delay of at least a quarter. This evidence is similar to, and in line with, the evidence in this paper about the negative effect of lagged money supply.
Finally two papers, not yet referred to, dwell on the effect of inflation uncertainty in the bond market [40Brenner M, Landskroner Y. Inflation uncertainties and return on bonds Economica 1983; 50: 463-8.
[http://dx.doi.org/10.2307/2554307] , 41Wright JH. Term premia and inflation uncertainty Empirical evidence from an international panel dataset Ame Eco Rev 2011; 101: 1514-34.
[http://dx.doi.org/10.1257/aer.101.4.1514] ]. Both [40Brenner M, Landskroner Y. Inflation uncertainties and return on bonds Economica 1983; 50: 463-8.
[http://dx.doi.org/10.2307/2554307] , 41Wright JH. Term premia and inflation uncertainty Empirical evidence from an international panel dataset Ame Eco Rev 2011; 101: 1514-34.
[http://dx.doi.org/10.1257/aer.101.4.1514] ] find that this effect is statistically significant in the bond market, although the evidence in [40Brenner M, Landskroner Y. Inflation uncertainties and return on bonds Economica 1983; 50: 463-8.
[http://dx.doi.org/10.2307/2554307] ] is not that strong and depends on the variable that proxies for uncertainty, and although [41Wright JH. Term premia and inflation uncertainty Empirical evidence from an international panel dataset Ame Eco Rev 2011; 101: 1514-34.
[http://dx.doi.org/10.1257/aer.101.4.1514] ] mention that other factors like the flight to quality and the bond purchases of foreign central banks seem to add explanatory power during the recent period.
CONCLUSION
The purpose of this paper is to test the statistical significance of three variables that are usually posited in parts of the literature to be determinants of stock returns. These variables are: inflation, inflation uncertainty, and the fluctuation in the US dollar. Strong statistical evidence is presented that neither US inflation nor US inflation uncertainty explains significantly US stock returns. However, in what concerns the effect of the US dollar, denoted by the phrase economic exposure, the evidence is also strong that there are two regimes, made out of samples before and after July 1998. In the old sample the relative change in the US dollar is the only variable without a statistical explanatory power, while in the recent sample this variable is the only one that has a statistical explanatory power. In this latter sample a depreciation of the US dollar raises equity returns. It is estimated that a 1% depreciation of the US dollar raises total corporate profits and stock returns by about 1.6%. This effect, which is statistically highly significant, runs counter the evidence in the literature of no relation, or even of a negative relation. In addition, the paper has also established that money supply growth has a negative, statistically significant, and delayed effect on stock returns, whatever the specification or model adopted, and that this feature runs against market efficiency. There remains to clarify the theoretical reason why there is a breakpoint on July 1998, and why this date is a turning point for the relation between stock prices and the US dollar. Indeed this breakpoint occurs at the time when many countries were abandoning pegged exchange rates with the US dollar in the midst of the Asian financial crisis and subsequent speculative attacks on other currencies such as the Argentinian peso and the Russian rouble. Finally, a justification for the puzzling significant and negative delayed impact of money growth rates on stock returns should be found.
CONFLICT OF INTEREST
The author confirms that this article content has no conflict of interest.
NOTES
1 In [39Cebula R. A contemporary investigation of causality between the primary government budget deficit and the ex ante real long term interest rate in the US Banca Nazionale Del Lavoro Quarterly Review 2002; 223: 417-35.] Cebula concludes that the net effect of the adjusted money variable is indeterminate. However an accurate reading of his findings shows that the net effect of this variable on interest rates is indeed and unequivocally negative and that Cebula’s conclusion about indeterminacy is mistaken and unwarranted.
ACKNOWLEDGEMENTS
Declared none.
REFERENCES
| [1] | Azar SA. Inflation and stock returns Int J Acc Fin 2010; 2 (3/4): 254-74. |
| [2] | Azar SA. The spurious relation between inflation uncertainty and stock returns: Evidence from the U.S Rev Eco Fin 2013; 3(4): 99-109. |
| [3] | Dornbusch R, Fischer S. Exchange rates and the current account Ame Eco Rev 1980; 70: 960-71. |
| [4] | Frankel J. Monetary and portfolio balance models of exchange rate determination In: Bhandari JS, Putman BH, Eds. Economic interdependence and flexible exchange rates. MIT: Cambridge 1983; pp. 84-115. |
| [5] | Azar SA. US stocks and the US dollar Int J Fin Res 2013; 4(4): 91-106. |
| [6] | Azar SA. US stocks and the US dollar II Int Res J Fin Eco 2013; (117): 188-216. |
| [7] | Azar S A. Inflation and stock returns II Int J Eco Fin 2014; 6(1): 208-16. |
| [8] | Azar SA. The US Dow and the US dollar App Eco Let 2014; 21(10): 683-. [http://dx.doi.org/10.1080/13504851.2014.884690] |
| [9] | Williams JB. The theory of investment value. Cambridge: Harvard University Press 1938. |
| [10] | Gordon MJ, Shapiro L. Capital equipment analysis: The required rate of profit Manage Sci 1956; 3(1): 102-. [http://dx.doi.org/10.1287/mnsc.3.1.102] |
| [11] | Gordon M. Dividends, earnings and stock prices Rev Eco Stats 1959; 41(2): 99-105. [http://dx.doi.org/10.2307/1927792] |
| [12] | Gordon M. The investment, financing, and valuation of the corporation Homewood Irwin 1962. |
| [13] | Levi MD. International finance: The markets and financial management of multinational business. New York: McGraw-Hill 1990. |
| [14] | Hallerbach WG. Cross-and auto-correlation effects arising from averaging the case of US interest rates and equity duration App Fin Eco 2003; 13(4): 287-94. [http://dx.doi.org/10.1080/09603100210135720] |
| [15] | Baz J, Chacko G. Financial derivatives, pricing, applications, and mathematics. Cambridge: Cambridge University Press 2004. [http://dx.doi.org/10.1017/CBO9780511806643] |
| [16] | Phillips PCB, Perron P. Testing for a unit root in time series regression Biometrica 1988; 75 (2): 335-46. [http://dx.doi.org/10.1093/biomet/75.2.335] |
| [17] | EViews 8 In: Irvine. CA: IHS Global Inc 2013. |
| [18] | Brealey RA, Myers SC, Allen F. Principles of corporate finance In: Global edition. 11th. New York: McGraw-Hill 2014. |
| [19] | Bai J. Estimating multiple breaks one at a time Econ Theory 1997; 13: 315-52. [http://dx.doi.org/10.1017/S0266466600005831] |
| [20] | Bai J, Perron P. Estimating and testing linear models with multiple structural changes Econometrica 1998; 66: 47-78. [http://dx.doi.org/10.2307/2998540] |
| [21] | Dickey DA, Fuller WA. Distribution of the estimators for autoregressive time series with a unit root J Ame Stat Ass 1979; 4 (366): 427-31. |
| [22] | Hu X, Willett TD. The variability of inflation and real stock returns App Fin Eco 2000; 10 (6): 655-. [http://dx.doi.org/10.1080/096031000438006] |
| [23] | Lin SC. Inflation and real stock returns revisited Eco Inq 2009; 47 (4): 783-95. |
| [24] | Nelson DB. Conditional heteroskedasticity in asset returns: a new approach Economterica 1991; 59: 347-70. [http://dx.doi.org/10.2307/2938260] |
| [25] | Grubert H. Foreign taxes and the growing share of U.S. multinational company income abroad: Profits, not sales, are being globalized Nat Tax 2012; 65(2): 247-82. |
| [26] | Jorion P. The exchange-rate exposure of U.S. multinationals J Bus 1990; 63(3): 331-45. [http://dx.doi.org/10.1086/296510] |
| [27] | Lee B-S, Suh J. Exchange rate changes and the operating performance of multinationals Euro Fin Manage 2012; 18(1): 88-116. [http://dx.doi.org/10.1111/j.1468-036X.2009.00522.x] |
| [28] | Muller A, Verschoor WFC. European foreign exchange risk exposure Euro Fin Manage 2006; 12(2): 195-220. [http://dx.doi.org/10.1111/j.1354-7798.2006.00316.x] |
| [29] | Fisher I. The theory of interest. New York: MacMillan 1930. |
| [30] | Campbell J, Ammer J. What moves the stock and bond markets? A variance decomposition for long-term asset returns The J Fin 1993; 48(1): 3-37. [http://dx.doi.org/10.1111/j.1540-6261.1993.tb04700.x] |
| [31] | Mehra YP. Some key empirical determinants of short-term nominal interest rates Federal Res Bank Richmond Econ Quarterly 1995; 81(3): 33-51. |
| [32] | Kasibhatla KM. The relation between inflation and interest rates: A cointegration analysis Int J Fin 2011; 23(4): 7034-44. |
| [33] | Crowder WJ, Hoffman DL. The long-run relationship between nominal interest rates and inflation: The Fisher equation revisited J Money Credit Bank 1996; 28(1): 102-8. [http://dx.doi.org/10.2307/2077969] |
| [34] | Barr DG, Pesaran B. An assessment of the relative importance of
real interest rates, inflation, and term premiums in determining the
prices of real and nominal U.K. bonds Rev Eco Stat 1997; 79(3): 362-6. [http://dx.doi.org/10.1162/003465300556931] |
| [35] | Bandholz H, Clostermann J, Seitz F. Explaining the US bond yield conundrum App Fin Eco 2009; 19: 539-0. [http://dx.doi.org/10.1080/09603100801964370] |
| [36] | Bae SC, Yi TD. Structural breaks and the Fisher hypothesis in bond and stock markets App Fin Eco 2009; 19: 1961-73. [http://dx.doi.org/10.1080/09603100903282614] |
| [37] | Malliaropulos D. A note on non-stationarity, structural breaks, and the Fisher effect J Bank Financ 2000; 24: 695-707. [http://dx.doi.org/10.1016/S0378-4266(99)00064-3] |
| [38] | Cebula R. An empirical analysis of the impact of federal budget
deficits on long-term nominal interest rate yields, 1973.2-1995.4,
using alternative expected inflation measures Rev Fin Eco 1998; 7(1): 55-64. [http://dx.doi.org/10.1016/S1058-3300(99)80145-1] |
| [39] | Cebula R. A contemporary investigation of causality between the primary government budget deficit and the ex ante real long term interest rate in the US Banca Nazionale Del Lavoro Quarterly Review 2002; 223: 417-35. |
| [40] | Brenner M, Landskroner Y. Inflation uncertainties and return on bonds Economica 1983; 50: 463-8. [http://dx.doi.org/10.2307/2554307] |
| [41] | Wright JH. Term premia and inflation uncertainty Empirical evidence from an international panel dataset Ame Eco Rev 2011; 101: 1514-34. [http://dx.doi.org/10.1257/aer.101.4.1514] |
Endorsements
Table of Contents
- INTRODUCTION
- THE MODELPt=Dt1(kg)=(1g)Dt(kg)=(1g)Et(kg)d(P)=Ptd(t)Pkd(k)PEd(E)=Ptd(t)Et1(kg)2d(k)(1g)(kg)d(E)d(P)P=PPtd(t)1(kg)d(k)1Ed(E)=PPtd(t)1(kg)d(k)d(E)E=PPtd(t)1D/Pd(k)d(E)EEf=AXd(Ef)/Efd(X)/X==d(q)/qd(X)/Xd(P)P=d(k)(kg)d(Ed)Ed(Ef)E=d(k)(kg)d(Ed)Ed(1)d(X)X(log(P))=1(kg)(k)(log(Ed))(log(X))=(k)(log(Ed))(log(X))
- DATA SOURCE
- THE DELAYED EFFECT OF MONEY GROWTH RATES
- THE IRRELEVANCE OF INFLATION
- THE IRRELEVANCE OF INFLATION UNCERTAI-NTY
- THE EFFECT OF THE US DOLLAR (ECONOMIC EXPOSURE)d(Ef)Ef=d(E)(1)E=d(X)Xd(E)E=(1)d(X)X
- THE EVIDENCE FROM THE INTEREST RATE MARKETSR=ere
- CONCLUSION
- CONFLICT OF INTEREST