- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Atmospheric Science Journal
(Discontinued)
ISSN: 1874-2823 ― Volume 14, 2020
Low-Frequency Atmospheric Gravity Waves from Vertical Tectonic Deformation During Two Recent Chilean Megathrust Events: the 2010 Maule (Mw8.8), and 2014 Iquique (Mw8.2) Earthquakes
Takeshi Mikumo1, *, Takuo Shibutani2, Makiko Iwakuni3, Nobuo Arai4
Abstract
Background:
Low-frequency atmospheric waves with gravity modes were recorded within 6.5 hours and 4.7 hours after two recent Chilean megathrust events, the 2010 Maule (Mw = 8.8), and 2014 Iquique (Mw = 8.2) earthquakes, respectively, at several microbarograph stations of the International Monitoring System (IMS) in South America and its surrounding regions.
Method:
Their apparent phase velocity up to the epicentral distances of 7,404 km and 6,481 km was found to be around 319 m/s and 337 m/s, respectively for the gravity modes after the two earthquakes. We tried to construct synthetic waveforms to be recorded at some of these microbarograph stations, incorporating various seismic source characteristics of the two earthquakes, and also a standard sound velocity structure up to a height of 220 km above the ground surface. The comparison appears to show some agreement between the observed and synthetic waveforms at least for the first 22 min for appropriate combinations of these source parameters.
Results:
The results indicate that the observed atmospheric gravity waves at the initial stage appear to have actually been excited at the source region of these megathrust earthquakes.
Conclusion:
The average rise time of vertical tectonic movement at the source region, which is estimated to be from the observed gravity waves, appears to be in the range between 2 and 3 min.
Article Information
Identifiers and Pagination:
Year: 2017Volume: 11
First Page: 71
Last Page: 87
Publisher Id: TOASCJ-11-71
DOI: 10.2174/1874282301711010071
Article History:
Received Date: 20/01/2017Revision Received Date: 28/03/2017
Acceptance Date: 04/04/2017
Electronic publication date: 27/07/2017
Collection year: 2017
open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution 4.0 International Public License (CC-BY 4.0), a copy of which is available at: https://creativecommons.org/licenses/by/4.0/legalcode. This license permits unrestricted use, distribution, and reproduction in any medium, provided the original author and source are credited.
* Address correspondence to this author at the Kyoto University, Uji, Kyoto 611-0001, Japan; Tel/Fax: +8-774-32-0072; E-mail: mikumo@maia.eonet.ne.jp
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 20-01-2017 |
Original Manuscript | Low-Frequency Atmospheric Gravity Waves from Vertical Tectonic Deformation During Two Recent Chilean Megathrust Events: the 2010 Maule (Mw8.8), and 2014 Iquique (Mw8.2) Earthquakes | |
1. INTRODUCTION
The 2010 earthquake (Mw = 8.8) took place off the west coast of the Maule region in southwestern Chile (-35.909°N, -72.733°E, due to Universidad de Chile) on February 27, 2010, 06:34 UTC, as shown in Fig. (1a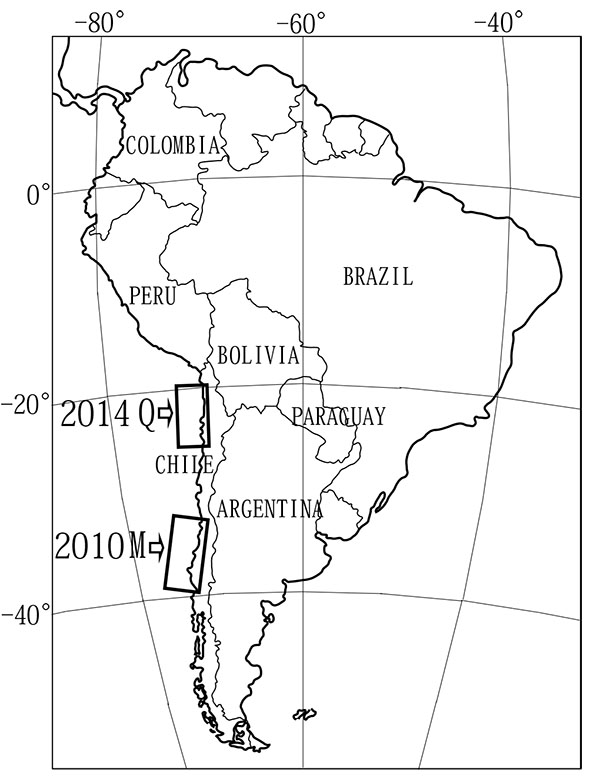 ). This region is located just north to the source region of the giant 1960 Valdivia, Chile earthquake (Mw = 9.5). Far-field seismic observations [1Lay T, Ammon CJ, Kanamori H, Koper KD, Sufri O, Hutko AR. Teleseismic inversion for rupture process of the 27 February 2010 Chile (Mw8.8) earthquake. Geophys Res Lett 2010; 37: L13301.
). This region is located just north to the source region of the giant 1960 Valdivia, Chile earthquake (Mw = 9.5). Far-field seismic observations [1Lay T, Ammon CJ, Kanamori H, Koper KD, Sufri O, Hutko AR. Teleseismic inversion for rupture process of the 27 February 2010 Chile (Mw8.8) earthquake. Geophys Res Lett 2010; 37: L13301.
[http://dx.doi.org/10.1029/2010GL043379] -5Lorito S, Romano F, Atzori S, et al. Limited overlap between the seismic gap and coseismic slip of the great 2010 Chile earthquake. Nat Geosci 2011; 4: 173-7.
[http://dx.doi.org/10.1038/ngeo1073] ] provided the general features of the fault rupture process, and various geodetic measurements including a radar technique clarified the spatial extent of the rupture zone [6Tong X, Sandwell D, Lutteri K, et al. The 2010 Maule, Chile earthquake: downdip rupture limit revealed by space geodesy. Geophys Res Lett 2010; 37: L24311.
[http://dx.doi.org/10.1029/2010GL045805] -10Moreno M, Melnik D, Rosenau M, et al. Toward understanding tectonic control on the Mw 8.8 2010 Maule, Chile earthquake. Earth Planet Sci Lett 2012; 321-322: 152-65.]. These various measurements including GPS, InSAR, and near-field land-level changes clearly suggested that the rupture zone over the Nazca-South America plate boundary extends for about 500 km in the NNE-SSW direction nearly parallel to the trench axis and sea-shore line, and for about 200 km in the E-W direction. Synthetic inversion of all these data has suggested a maximum coseismic slip of 16 m on the dipping fault plane in its northern segment and about 10 m over two patches in its southern segment, and this slip pattern yields maximum ground uplift of 4.0 m and subsidence of 0.85 m at the two sides of the rupture zone [10Moreno M, Melnik D, Rosenau M, et al. Toward understanding tectonic control on the Mw 8.8 2010 Maule, Chile earthquake. Earth Planet Sci Lett 2012; 321-322: 152-65.].
 |
Fig. (1a) Index map. South America continent, and the location of two source regions of the 2010 Maule earthquake (M) and the 2014 Iquique earthquake (Q). |
The second 2014 Iquique earthquake (Mw = 8.2) occurred also in the west coast of northern Chile (-19.642°N, -70.817°E at a depth of 21.9 km, due to USGS), as also shown in Fig. (1a ). It took on April 1, 2014, 23:46 UTC, about 1600 km north of the 2010 Maule earthquake. This region has been identified as the northern Chile seismic gap [11Kelleher JA. Rupture zone of large South American earthquakes and some predictions. J Geophys Res 1972; 77: 2087-103.], [12Nishenko SP. Seismic potential for large and great interplate earthquakes along the Chilean and southern Peruvian margins of South America: a quantitative reappraisal. J Geophys Res 1985; 90: 3589-615.], since a megathrust earthquake of 1877 with a magnitude of 8.7 - 8.9 [13Comite D, Pardo M. Reappraisal of great historical earthquakes in the northern Chile and southern Peru seismic gaps. Nat Hazards 1991; 4: 23-44.
). It took on April 1, 2014, 23:46 UTC, about 1600 km north of the 2010 Maule earthquake. This region has been identified as the northern Chile seismic gap [11Kelleher JA. Rupture zone of large South American earthquakes and some predictions. J Geophys Res 1972; 77: 2087-103.], [12Nishenko SP. Seismic potential for large and great interplate earthquakes along the Chilean and southern Peruvian margins of South America: a quantitative reappraisal. J Geophys Res 1985; 90: 3589-615.], since a megathrust earthquake of 1877 with a magnitude of 8.7 - 8.9 [13Comite D, Pardo M. Reappraisal of great historical earthquakes in the northern Chile and southern Peru seismic gaps. Nat Hazards 1991; 4: 23-44.
[http://dx.doi.org/10.1007/BF00126557] ]. Aftershocks of this mainshock event extend nearly parallel to the trench axis for about 150-200 km. Teleseismic P-waves and W-phase inversions from global seismic recordings suggested a maximum slip of ~ 2 - 6.7 m on a thrust fault plane dipping with 14°, indicating a dip of the subducting plate in this region [14An C, Sepulveda I, Liu PL. Tsunami source and its validation of the 2014 Iquique, Chile, earthquake. Geophys Res Lett 2014; 41: 3988-94.
[http://dx.doi.org/10.1002/2014GL0650567] ], while the inversion of Tsunami data suggested a slip of 5 - 7 m around a depth of 23 km in a more concentrated area of 60 km by 40 km [15Gusman AR, Murotani S, Satake K, et al. Fault slip distribution of the 2014 Iquique, Chile, earthquake estimated from ocean-wide Tsunami waveforms and GPS data. Geophys Res Lett 2015; 42: 1053-60.
[http://dx.doi.org/10.1002/2014GL062604] ]. This mechanism should have caused some amount of uplift and subsidence near the bottom of the oceanic trench and a part of the inland region, although their amounts have not been estimated from geodetic surveys, unlike the case of the Maule earthquake.
With these circumstances, low-frequency atmospheric pressure waves were identified during 6.5 hours and 4.7 hours after the first and second great earthquakes, respectively, by sensitive microbarographs at several global International Monitoring System (IMS) stations located in South America and its surroundings, as shown in 1b . It is to be mentioned here that similar observations of low-frequency atmospheric waves have been recorded after three megathrust events, since the 1964 Alaskan earthquake (Mw = 9.2) [16Bolt BA. Seismic air waves from the great Alaskan earthquake. Nature 1964; 202: 1095-6.
. It is to be mentioned here that similar observations of low-frequency atmospheric waves have been recorded after three megathrust events, since the 1964 Alaskan earthquake (Mw = 9.2) [16Bolt BA. Seismic air waves from the great Alaskan earthquake. Nature 1964; 202: 1095-6.
[http://dx.doi.org/10.1038/20211095a0] , 17Mikumo T. Atmospheric pressure waves and tectonic deformation associated with the Alaskan earthquake of March 28, 1964. J Geophys Res 1968; 73: 2009-25.
[http://dx.doi.org/10.1029/JB0i006p02009] ], the 2004 Sumatra-Andaman earthquake (Mw = 9.2) [18Mikumo T, Shibutani T, Le Pichon A, et al. Low-frequency acoustic-gravity waves from coseismic vertical deformation associated with the 2004 Sumatra-Andaman earthquake (Mw=9.2). J Geophys Res 2008; 113: B12402.
[http://dx.doi.org/10.1029/2008JB005710] , 19Raveloson A, Wang R, Kind R, Ceranna L, Yuan X. Seismic and gravity signals from the source of the 2004 Indian Ocean Tsunami. Nat Hazards Earth Syst Sci 2012; 12: 287-94.], and the 2011 great Off-Tohoku earthquake (Mw = 9.0) [20Arai N, Iwakuni M, Watada S, Imanishi Y, Murayama T, Nogami M. Atmospheric boundary waves excited by the Tsunami generation related to the 2011 great Tohoku-Oki earthquake. Geophys Res Lett 2011; 38: L00G18.
[http://dx.doi.org/10.1029/2011 GL049146] , 21Mikumo T, Garces M, Shibutani T, Morii W, Okawa T, Ishihara Y. Acoustic-gravity waves from the source region of the 2011 great Tohoku earthquake (Mw=9.0). J Geophys Res 2013; 118: 1534-45.
[http://dx.doi.org/10.1002/jgrb.50143] ].
 |
Fig. (1b) Location of IMS stations in and around South America. |
In the present article, we try to find the evidence of observations for low-frequency gravity waves propagating from each of the source regions of the above two great earthquakes through the atmosphere to some of these microbarograph stations. We also calculate synthetic waveforms, incorporating various seismic source characteristics described above and based on a standard atmospheric sound velocity structure up to a height of 220 km. Our main purpose here is to demonstrate that the observed atmospheric gravity waves have actually been generated from some part of the source regions of the two great earthquakes, and also try to elucidate, if possible, the overall source characteristics for exciting the low-frequency atmospheric waves from these megathrust events.
2. OBSERVATIONS OF PROPAGATING ATMOSPHERIC WAVES
The IMS stations shown in Fig. (1b ) that recorded low-frequency atmospheric pressure waves from the two earthquakes are summarized in Tables (1 and 2), respectively. These stations are located in South America and its surroundings in the distance range from the epicenter between 1,813 km and 7,684 km in the case of the 2010 Maule earthquake Fig. (2a
) that recorded low-frequency atmospheric pressure waves from the two earthquakes are summarized in Tables (1 and 2), respectively. These stations are located in South America and its surroundings in the distance range from the epicenter between 1,813 km and 7,684 km in the case of the 2010 Maule earthquake Fig. (2a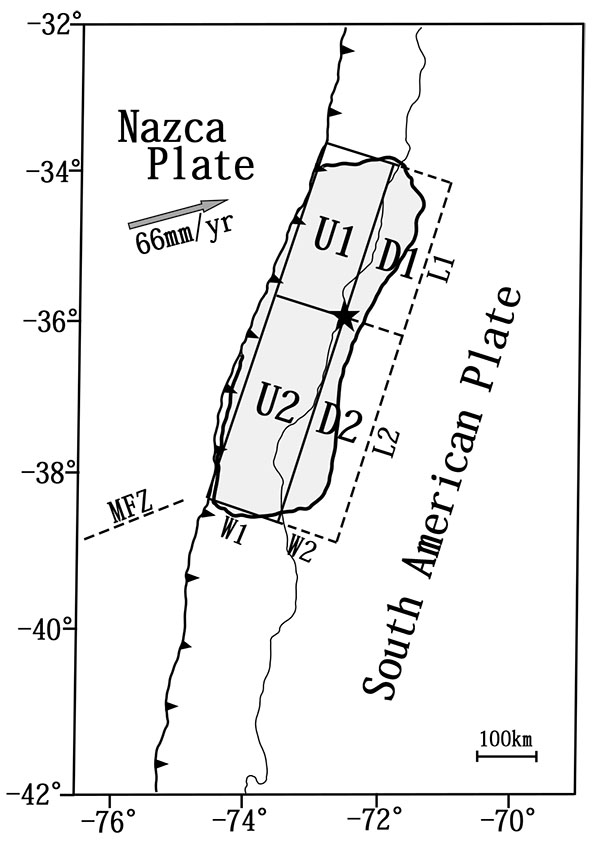 ), and between 1,569 km and 6,481 km in the case of the 2014 Iquique earthquake Fig. (2b
), and between 1,569 km and 6,481 km in the case of the 2014 Iquique earthquake Fig. (2b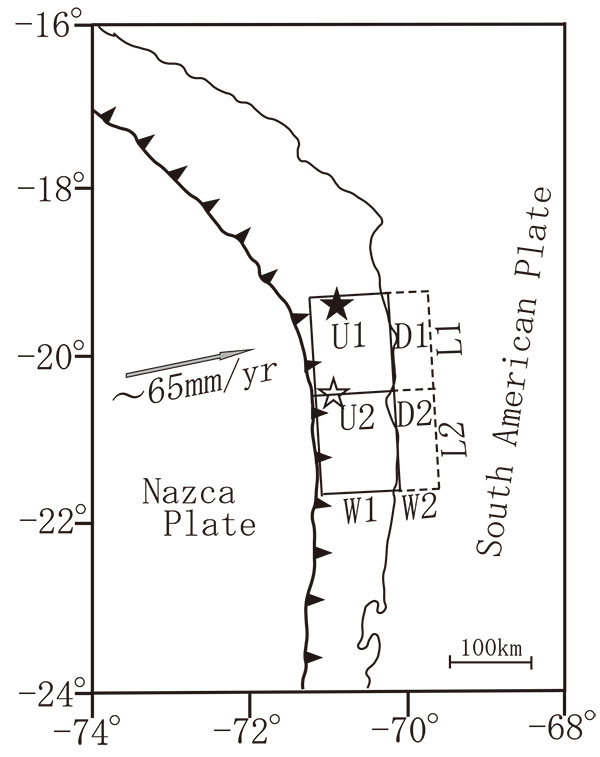 ). Four of these stations are located within the South America continent, another four are on islands in the Atlantic Ocean northeast or east of it, and the other three are located on islands in the southwestern Pacific Ocean west of the continent. However, observed records at some of these stations are perturbed by quite large atmospheric noise and probably by high oceanic waves. Accordingly, in the present analysis, we selected each four stations with relatively less perturbed and coherent waves from the two events.
). Four of these stations are located within the South America continent, another four are on islands in the Atlantic Ocean northeast or east of it, and the other three are located on islands in the southwestern Pacific Ocean west of the continent. However, observed records at some of these stations are perturbed by quite large atmospheric noise and probably by high oceanic waves. Accordingly, in the present analysis, we selected each four stations with relatively less perturbed and coherent waves from the two events.
In the upper two traces of (Figs. 3 , 4
, 4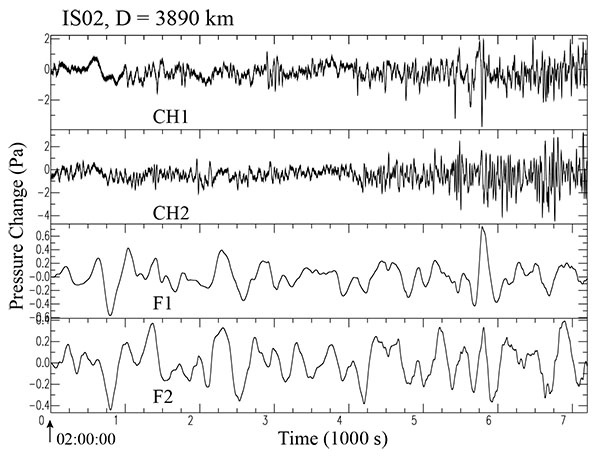 ), are shown each two components of the original records of pressure perturbation over a time interval of 7,200 sec (2 hours), which have been observed at IS08 station during the Maule earthquake, and at IS02 station during the Iquique event, respectively. The long time length has been taken to look at how are atmospheric noise and possible arrival of target signals during the two hours. Because these records include high-frequency noise and long-term inclinations, as shown in each of these upper traces, we apply a second-order Butterworth bandpass-filter to each two channels of the above original records, with a unit amplitude over a frequency range between 1.19 and 3.70 mHz (or between 14.0 and 4.5 min), which could cover the frequency range of gravity waves propagating in the lower atmosphere [22Harkrider DG. Theoretical and observed acoustic-gravity waves from explosive sources in the atmosphere. J Geophys Res 1964; 69: 5295-321.
), are shown each two components of the original records of pressure perturbation over a time interval of 7,200 sec (2 hours), which have been observed at IS08 station during the Maule earthquake, and at IS02 station during the Iquique event, respectively. The long time length has been taken to look at how are atmospheric noise and possible arrival of target signals during the two hours. Because these records include high-frequency noise and long-term inclinations, as shown in each of these upper traces, we apply a second-order Butterworth bandpass-filter to each two channels of the above original records, with a unit amplitude over a frequency range between 1.19 and 3.70 mHz (or between 14.0 and 4.5 min), which could cover the frequency range of gravity waves propagating in the lower atmosphere [22Harkrider DG. Theoretical and observed acoustic-gravity waves from explosive sources in the atmosphere. J Geophys Res 1964; 69: 5295-321.
[http://dx.doi.org/10.1029] ]. The above frequency range does not cover the propagating acoustic modes, because the modes are heavily contaminated by various noise in the present case. These filtered traces are aligned in the lower two traces of each of the above figures.
The next step is to compare above filtered channels at each station with the synthetic waveforms given in Section 4, in order to discuss the source characteristics of the above two megathrust earthquakes, after estimating approximate propagation phase velocity of the gravity waves radiated from these events.
3. WAVEFORM MODELING
We perform waveform modeling for the above filtered records of pressure perturbation, to confirm that the observed waves have been actually excited somewhere within the extensive source regions of these great earthquakes, and propagated through the lower to middle atmosphere to the observation stations. To do this, we incorporate such a realistic thermal structure as the US Standard Atmosphere, formerly called the ARDC atmospheric thermal model. The structure of the atmosphere is composed mainly of four layers. The temperature decreases first up an altitude of 15 km in the troposphere, increases up to 45 - 50 km in the stratosphere, then decreases again at 80 - 90 km in the mesosphere, and finally the temperature increases rapidly in the thermosphere up to 220 km. Although somewhat modified models, such as CIRA [23Yeh KC, Liu C. Acoustic-gravity waves in the upper atmosphere. Rev Geophys Space Phys 1974; 12: 193-216.], MISISE [24Hedin AE. Extension of the MSIS thermospheric model into middle and lower atmosphere. J Geophys Res 1991; 69: 1159-72.], and NRL-C2Z [25Drob DP, Picone M, Garces MA. The global morphology of infrasound propagation. Geophys Res Lett 2003; 108: 4680.
[http://dx.doi.org/10.1029/2002JD003307] ] have been presented to date, we refer to the US standard structure as a more global scale structure to discuss lower frequency waves. For the ARDC standard atmosphere, the phase and group velocities of several acoustic and gravity modes have been calculated [26Press F, Harkrider DG. Propagation of acoustic-gravity waves in the atmosphere J Geophys Res 1962; 67: 3889-939.
[http://dx.doi.org/10.1029/JZ 67i010p03889] , 27Pefffer RI, Zarichny J. Acoustic-gravity wave propagation in the atmosphere with two sound channels. Pure Appl Geophys 1963; 55: 175-99.], where the air density is assumed to decrease exponentially with altitude. In addition, Harkrider [22Harkrider DG. Theoretical and observed acoustic-gravity waves from explosive sources in the atmosphere. J Geophys Res 1964; 69: 5295-321.
[http://dx.doi.org/10.1029] ] also calculated the dynamic response of the atmosphere to a point source and a receiver both located on the ground surface, by approximating the above thermal structure by 39 horizontally stratified, isothermal layers terminated either with the isothermal half-space or with the free surface at an altitude of 220 km. In the present article, we assume the former case in view of our previous test calculations [18Mikumo T, Shibutani T, Le Pichon A, et al. Low-frequency acoustic-gravity waves from coseismic vertical deformation associated with the 2004 Sumatra-Andaman earthquake (Mw=9.2). J Geophys Res 2008; 113: B12402.
[http://dx.doi.org/10.1029/2008JB005710] ].
The propagation of acoustic-gravity waves in the lower to middle atmosphere can be described by the following atmospheric transfer function, A(ω) exp[− iϕA(ω)], where,
 |
(1) |
AAj(ω) is the dynamic response of the atmosphere to a surface point source and receiver, k is the wave number, r0 is the distance from the source to the receiver, and Cj(ω) is the phase velocity, with j indicating the mode number. These functions have been calculated for several acoustic and gravity modes [18Mikumo T, Shibutani T, Le Pichon A, et al. Low-frequency acoustic-gravity waves from coseismic vertical deformation associated with the 2004 Sumatra-Andaman earthquake (Mw=9.2). J Geophys Res 2008; 113: B12402.
[http://dx.doi.org/10.1029/2008JB005710] -21Mikumo T, Garces M, Shibutani T, Morii W, Okawa T, Ishihara Y. Acoustic-gravity waves from the source region of the 2011 great Tohoku earthquake (Mw=9.0). J Geophys Res 2013; 118: 1534-45.
[http://dx.doi.org/10.1002/jgrb.50143] ], and a few examples of the Green’s functions from a point source to a far-field station have been shown in the case of the 2004 Sumatra-Andaman earthquake [18Mikumo T, Shibutani T, Le Pichon A, et al. Low-frequency acoustic-gravity waves from coseismic vertical deformation associated with the 2004 Sumatra-Andaman earthquake (Mw=9.2). J Geophys Res 2008; 113: B12402.
[http://dx.doi.org/10.1029/2008JB005710] ]. Beside the atmospheric transfer function, the observed waveforms should include the effects of the source time function, the dimension of the source region including the velocity of its expansion, and the instrumental response as indicated below.
If we assume a linear system coupled between the solid earth, the sea or land surface, and the atmosphere, then the pressure perturbation that would be observed at any station in the far-field, compared with the source dimension and the wavelength, can be written in the time domain as in the following equations [18Mikumo T, Shibutani T, Le Pichon A, et al. Low-frequency acoustic-gravity waves from coseismic vertical deformation associated with the 2004 Sumatra-Andaman earthquake (Mw=9.2). J Geophys Res 2008; 113: B12402.
[http://dx.doi.org/10.1029/2008JB005710] , 21Mikumo T, Garces M, Shibutani T, Morii W, Okawa T, Ishihara Y. Acoustic-gravity waves from the source region of the 2011 great Tohoku earthquake (Mw=9.0). J Geophys Res 2013; 118: 1534-45.
[http://dx.doi.org/10.1002/jgrb.50143] ],
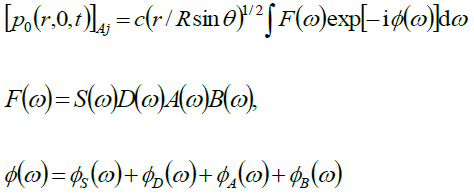 |
(2) |
where S(ω), D(ω), A(ω), and B(ω) are the source time spectrum, the source finiteness spectrum, the atmospheric transfer function defined as in equation (1), and the barograph response, respectively. ϕ (ω)s are their phase spectra, respectively. Here, c = 2(2/π) 1/2 is simply a numerical constant derived from Harkrider’s formulations [22Harkrider DG. Theoretical and observed acoustic-gravity waves from explosive sources in the atmosphere. J Geophys Res 1964; 69: 5295-321.
[http://dx.doi.org/10.1029] ], and (r/Rsinθ)1/2 is the approximate curvature correction for the effect of energy spreading over a spherical earth instead of a flat surface, with the distance r to the recording station from the source, the Earth’s radius R, and the spherical colatitude of the station θ. S(ω) for pressure perturbation includes the sound velocity c0 and air density ρ0 near the ground surface and the rise time of vertical displacement τ. D(ω) includes the source dimensions Li and Wi of the assumed rectangular source, the expanding velocity ν, and β the azimuth from the source to the station with respect to the direction of source expansion. These functions, including the parameters not explicitly mentioned here, have been calculated for various cases, and are shown in [18Mikumo T, Shibutani T, Le Pichon A, et al. Low-frequency acoustic-gravity waves from coseismic vertical deformation associated with the 2004 Sumatra-Andaman earthquake (Mw=9.2). J Geophys Res 2008; 113: B12402.
[http://dx.doi.org/10.1029/2008JB005710] , 21Mikumo T, Garces M, Shibutani T, Morii W, Okawa T, Ishihara Y. Acoustic-gravity waves from the source region of the 2011 great Tohoku earthquake (Mw=9.0). J Geophys Res 2013; 118: 1534-45.
[http://dx.doi.org/10.1002/jgrb.50143] ].
4. COMPARISON BETWEEN THE OBSERVED AND SYNTHETIC WAVEFORMS
Our next step is to incorporate the various source parameters of these great earthquakes into the calculation of synthetic waveforms, and then to compare them with the corresponding observed waveforms of pressure perturbation from the two different earthquakes, respectively. This is to elucidate the generation mechanism of low-frequency atmospheric pressure waves and also the possible features of coseismic vertical crustal deformation associated with these megathrust earthquakes. In this sense, we compare the two megathrust earthquakes that took place in the same subduction zone over the Nazca-South America plate boundary.
4.1. 2010 Maule Earthquake
For this earthquake, the location, the entire source dimension, and total coseismic slip obtained from three different types of geodetic measurements, are shown in Moreno et al. [10Moreno M, Melnik D, Rosenau M, et al. Toward understanding tectonic control on the Mw 8.8 2010 Maule, Chile earthquake. Earth Planet Sci Lett 2012; 321-322: 152-65.]. The overall source dimension extending for about 500 km in the NNE-SSW direction nearly parallel to the trench axis may be separated into the northern and southern segments with respect to the location of the epicenter, and the width of about 200 km in the E-W direction may be separated by two zones of ground uplift and subsidence, respectively, as shown in Fig. (2a ). We denote these four zones as U1, U2, D1, and D2, respectively, which are specified with their approximate lengths L1 = 220 km and L2 = 280 km and their widths W1 = 150 km and W2 = 50 km. Average tectonic ground uplifts in the two zones enclosed by L1 and W1 and by L2 and W1 are successively varied within possible values between 0.5 m and 3.5 m, as indicated in Table (3). Average subsidences within two zones enclosed by L1 and W2 and by L2 and W2 are fixed as -1.0 m and -0.5 m. Also assumed is the average velocity of source spreading from the epicenter as 2.5 km/s. We confirmed by a number of trial calculations that these fixed values did not have large effects on the synthetic waveforms, as shown in our previous studies [18Mikumo T, Shibutani T, Le Pichon A, et al. Low-frequency acoustic-gravity waves from coseismic vertical deformation associated with the 2004 Sumatra-Andaman earthquake (Mw=9.2). J Geophys Res 2008; 113: B12402.
). We denote these four zones as U1, U2, D1, and D2, respectively, which are specified with their approximate lengths L1 = 220 km and L2 = 280 km and their widths W1 = 150 km and W2 = 50 km. Average tectonic ground uplifts in the two zones enclosed by L1 and W1 and by L2 and W1 are successively varied within possible values between 0.5 m and 3.5 m, as indicated in Table (3). Average subsidences within two zones enclosed by L1 and W2 and by L2 and W2 are fixed as -1.0 m and -0.5 m. Also assumed is the average velocity of source spreading from the epicenter as 2.5 km/s. We confirmed by a number of trial calculations that these fixed values did not have large effects on the synthetic waveforms, as shown in our previous studies [18Mikumo T, Shibutani T, Le Pichon A, et al. Low-frequency acoustic-gravity waves from coseismic vertical deformation associated with the 2004 Sumatra-Andaman earthquake (Mw=9.2). J Geophys Res 2008; 113: B12402.
[http://dx.doi.org/10.1029/2008JB005710] , 21Mikumo T, Garces M, Shibutani T, Morii W, Okawa T, Ishihara Y. Acoustic-gravity waves from the source region of the 2011 great Tohoku earthquake (Mw=9.0). J Geophys Res 2013; 118: 1534-45.
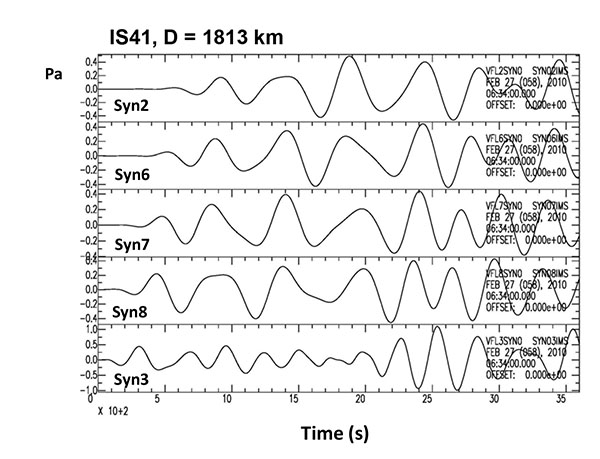
[http://dx.doi.org/10.1002/jgrb.50143] ]. Some of the above estimates are taken by referring to the geodetic measurements given in Table S2 of Moreno et al. [10Moreno M, Melnik D, Rosenau M, et al. Toward understanding tectonic control on the Mw 8.8 2010 Maule, Chile earthquake. Earth Planet Sci Lett 2012; 321-322: 152-65.]. The rest of the important parameter to be estimated is the rise time of vertical tectonic displacement in the source region, which could directly affect the calculated waveforms. These parameters are varied successively between 1.5 and 3.5 min in the zones of uplift, while fixing it as 2.0 min in the zone of subsidence as a first approximation. The synthetic waveforms for 5 possible cases with different rise times have been calculated, and the results are given for station IS41 in an additional PDF file [see Graph 1]. The five cases in Syn2 to Syn7 give generally similar waveforms, expecting that a good fit between the filtered and synthetic waveforms would be obtained at this station.
 |
Fig. (5a) Filtered and synthetic waveforms at station IS41 for the case of the 2010 Maule earthquake. Each of the upper two traces (F1 and F2) reproduces the filtered waveforms for the time interval of 3,600 sec (one hour). The lower two traces (S1 and S2) indicate the corresponding synthetic waveforms. The two synthetics S1 and S2 come from Syn7 and Syn2 in Table (3), respectively. The time shown below indicates the absolute time UTC, (a) IS41 (07:30-08:30). |
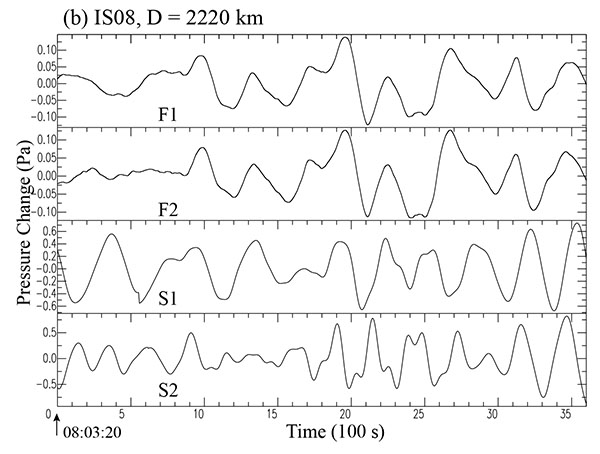 |
Fig. (5b) Filtered and synthetic waveforms at station IS08 for the case of the 2010 Maule earthquake. Each of the upper two traces (F1 and F2) reproduces the filtered waveforms for the time interval of 3,600 sec (one hour). The lower two traces (S1 and S2) indicate the corresponding synthetic waveforms. The two synthetics S1 and S2 come from Syn7 and Syn2 in Table (3), respectively. The time shown below indicates the absolute time UTC, (b) IS08 (08:03:20-09:03:20). |
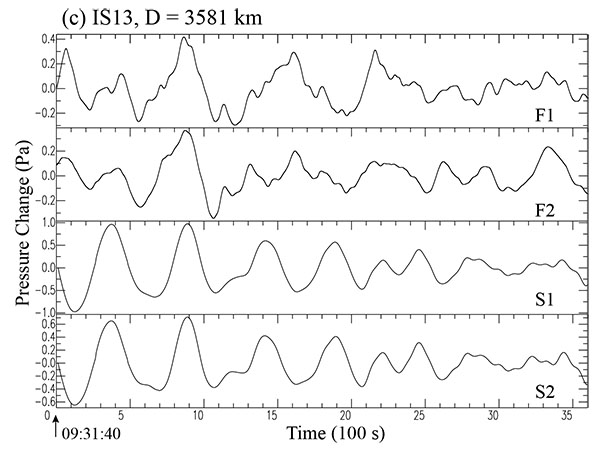 |
Fig. (5c) Filtered and synthetic waveforms at all 4 stations for the case of the 2010 Maule earthquake. Each of the upper two traces (F1 and F2) reproduces the filtered waveforms for the time interval of 3,600 sec (one hour). The lower two traces (S1 and S2) indicate the corresponding synthetic waveforms. The two synthetics S1 and S2 come from Syn7 and Syn2 in Table (3), respectively. The time shown in each bracket below indicates the absolute time UTC, (c) IS13 (09:31:40-10:31:40). |
 |
Fig. (5d) Filtered and synthetic waveforms at all 4 stations for the case of the 2010 Maule earthquake. Each of the upper two traces (F1 and F2) reproduces the filtered waveforms for the time interval of 3,600 sec (one hour). The lower two traces (S1 and S2) indicate the corresponding synthetic waveforms. The two synthetics S1 and S2 come from Syn7 and Syn2 in Table (3), respectively. The time shown in each bracket below indicates the absolute time UTC, (d) IS21 ( 13:00:00-14:00:00). |
Although the details of their comparison are described in each of the figure captions, the essential part of the filtered waveforms F1 or F2 at least for an initial time interval for about 22 min appears more or less partially simulated by the synthetic waveforms S1 (from Case Syn2 in Table 3 in most of these cases, whereas there remain some discrepancies between the filtered waveforms and the synthetics S2 (from Case Syn7 in Table 3 in these figures. This suggests that these latter cases S2 do not provide satisfactory explanations to the observations. From the first case, however, we would be able to infer that the average uplift in the northern and southern segments may be approximately 3.0 m and 1.5 m, respectively, and the corresponding rise time in the two zones may be around 3.0 min (See Table 3). There are some differences in their absolute amplitudes, however, for which we believe they are attributed to prevailing atmospheric conditions around these stations. We would say, however, that there are more or less generally satisfactory agreements between the filtered and synthetic waveforms S1 composed mainly of gravity modes, at least, for a limited time interval around the first part of about 22 min. The waveforms S1 in (Fig. 5b ) provides the best case.
) provides the best case.
4.2. 2014 Iquique Earthquake
For the 2014 Iquique earthquake, seismic source parameters have been estimated from various observations up to this time, from aftershock distribution, teleseismic waves and Tsunami observations, by several investigators mentioned below. The overall source dimension appears to extend for about 150 km [2Lay T, Yue H, Brodsky E, An C. The 1 April, 2014 Iquique Chile, Mw8.1 earthquake rupture sequence. Geophys Res Lett 2014; 41: 3818-25.
[http://dx.doi.org/10,1002/2014GL060238] ] to 200 km (USGS) in the N-S direction inferred from aftershock distribution, which appears to be almost parallel to the trench axis and the shore line in this region. Its width in the E-W direction may be about 100 km (USGS-NEIC). Preliminary inversions of teleseismic [2Lay T, Yue H, Brodsky E, An C. The 1 April, 2014 Iquique Chile, Mw8.1 earthquake rupture sequence. Geophys Res Lett 2014; 41: 3818-25.
[http://dx.doi.org/10,1002/2014GL060238] ] and Tsunami [14An C, Sepulveda I, Liu PL. Tsunami source and its validation of the 2014 Iquique, Chile, earthquake. Geophys Res Lett 2014; 41: 3988-94.
[http://dx.doi.org/10.1002/2014GL0650567] ] observations, and Tsunami and GPS observations [15Gusman AR, Murotani S, Satake K, et al. Fault slip distribution of the 2014 Iquique, Chile, earthquake estimated from ocean-wide Tsunami waveforms and GPS data. Geophys Res Lett 2015; 42: 1053-60.
[http://dx.doi.org/10.1002/2014GL062604] ], yield approximate spatial slip distribution on its dipping fault, but coseismic vertical displacements on land have not been estimated from geodetic surveys. We assume the maximum length of the uplifted zone as 200 km along the NNW-SSE direction (L1 + L2) with its maximum width (W1) to be 100 km beneath the oceanic region, and its maximum width of a possible subsided zone as 50 km (W2), as shown in Fig. (2b ). On the other hand, inversion of Tsunami data suggested a more concentrated source area of 60 km by 40 km near the hypocenter, in the total dimension of 200 km × 160 km, with a maximum slip of 5 to 7 m at a depth around 23 km [14An C, Sepulveda I, Liu PL. Tsunami source and its validation of the 2014 Iquique, Chile, earthquake. Geophys Res Lett 2014; 41: 3988-94.
). On the other hand, inversion of Tsunami data suggested a more concentrated source area of 60 km by 40 km near the hypocenter, in the total dimension of 200 km × 160 km, with a maximum slip of 5 to 7 m at a depth around 23 km [14An C, Sepulveda I, Liu PL. Tsunami source and its validation of the 2014 Iquique, Chile, earthquake. Geophys Res Lett 2014; 41: 3988-94.
[http://dx.doi.org/10.1002/2014GL0650567] ]. We also assume the rupture starting point at two different positions; one is located at the northwestern periphery of the source region (U1), and the other is assumed to lie at the northwestern central position of the entire source region. For these two possible cases, we refer them to unilateral (U) and bilateral (B) rupture extension, respectively, with a constant rupture velocity of 2.5 km/sec. We calculate synthetic waveforms for the two assumed cases. For the assumed bilateral case (B), we denote the divided four zones, U1, U2, D1, and D2, similar to the case for the 2010 Maule earthquake, with L1 = L2 = 100 km, W1 = 100 km and W2 = 50 km. For these subdivided zones, we assign average uplifts in the two zones enclosed by L1and W1 and by L2 and W1, as 3 m and 2 m, respectively, and average subsidence in the zones enclosed by L1 and W2 and by L2 and W2 are assumed as -1.0 and - 0.5 m, respectively, similar to the case of the Maule earthquake. The maximum positive displacement of the initial water elevation has been estimated as 1.54 m from the inversion analysis of Tsunami data [14An C, Sepulveda I, Liu PL. Tsunami source and its validation of the 2014 Iquique, Chile, earthquake. Geophys Res Lett 2014; 41: 3988-94.
[http://dx.doi.org/10.1002/2014GL0650567] ]. The rise times of vertical displacement in these zones are assumed here as 3.0, 2.0, 2.0, and 2.0 min, respectively. For the assumed unilateral case (U), on the other hand, L1 = 200 km and L2= 0 km, and the other parameters are fixed as in the same as in the case of (B). All these assumed parameters are given in Table 4.
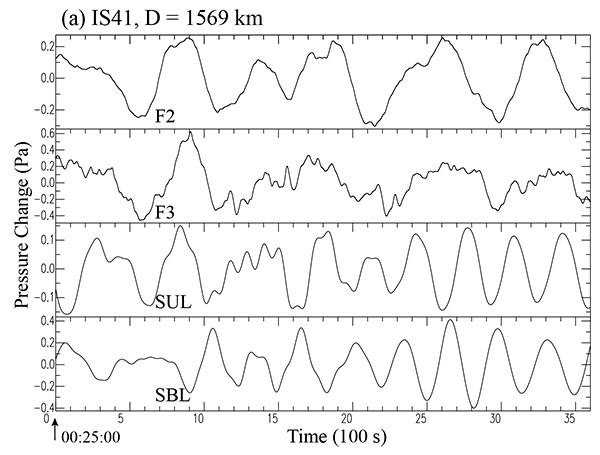 |
Fig. (6a) Filtered and synthetic waveforms at station IS41 for the case of the 2014 Iquique earthquake. The lower two traces (SUL and SBL) indicate the corresponding synthetic waveforms from Syn40 (unilateral case) and Syn51 (bilateral case), given in (Table 4). The time shown there indicates the absolute time UTC, (00:25-01:25). |
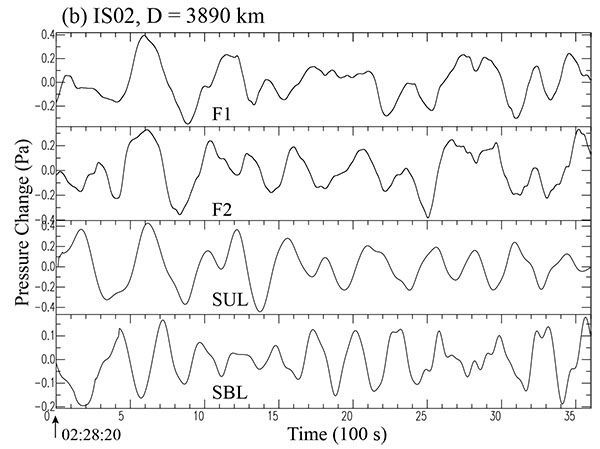 |
Fig. (6b) Filtered and synthetic waveforms at station IS02 for the case of the 2014 Iquique earthquake. The lower two traces (SUL and SBL) indicate the corresponding synthetic waveforms from Syn40 (unilateral case) and Syn51 (bilateral case), given in (Table 4). The time shown there indicates the absolute time UTC, (02:28:20-03:28:20). |
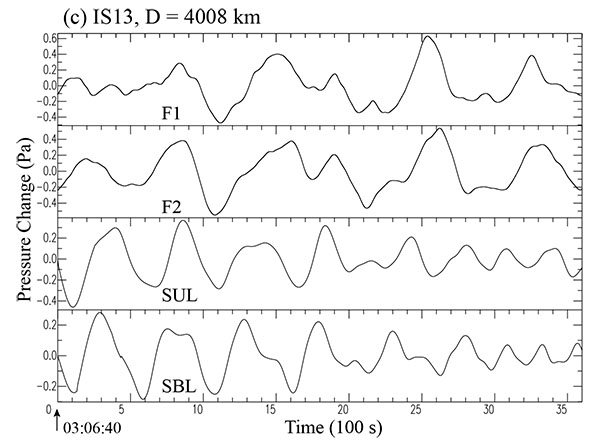 |
Fig. (6c) Filtered and synthetic waveforms at station IS13 for the case of the 2014 Iquique earthquake. The lower two traces (SUL and SBL) indicate the corresponding synthetic waveforms from Syn40 (unilateral case) and Syn51 (bilateral case), given in (Table 4). The time shown there indicates the absolute time UTC, (03:06:40-04:06:40). |
An example of the observed records of pressure perturbation are shown in the upper two traces at a selected station IS02 in Fig. (4 ), as indicated by CH1 and CH2. These records are then filtered as F1 and F2 as shown in the lower two traces, respectively. These filtered traces are then compared with the synthetic waveforms in Fig. (6b
), as indicated by CH1 and CH2. These records are then filtered as F1 and F2 as shown in the lower two traces, respectively. These filtered traces are then compared with the synthetic waveforms in Fig. (6b ). Likewise, the filtered waveforms for all 4 stations are then compared with the corresponding synthetic waveforms S1 and S2 in Figs. (6a
). Likewise, the filtered waveforms for all 4 stations are then compared with the corresponding synthetic waveforms S1 and S2 in Figs. (6a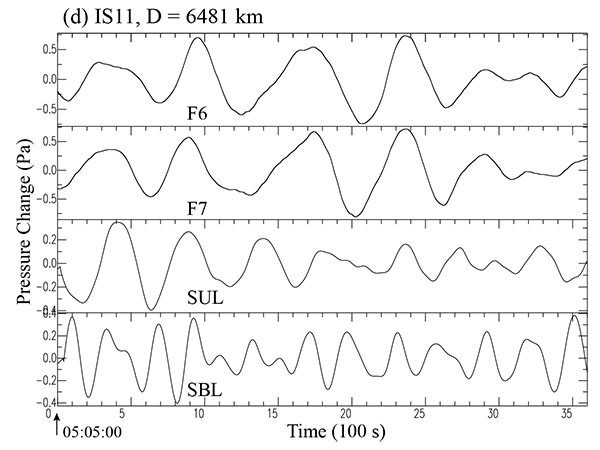 -6d
-6d ), respectively.
), respectively.
 |
Fig. (6d) Filtered and synthetic waveforms at station IS11 for the case of the 2014 Iquique earthquake. The lower two traces (SUL and SBL) indicate the corresponding synthetic waveforms from Syn40 (unilateral case) and Syn51 (bilateral case), given in (Table 4). The time shown there indicates the absolute time UTC, (05:05:00-06:05:00). |
The third (SUL) and fourth traces (SBL) in these figures indicate the corresponding synthetic waveforms for two different cases for assumed unilateral (U) and bilateral (B) rupture extension, respectively. Detailed comparisons between the filtered and synthetic waveforms are described in the figure captions. It appears that the filtered waveforms are more or less generally well simulated, by the synthetic waveforms (SUL) for the assumed unilateral case (U) from Syn40, at least, for a limited time interval of the first part of 22 min or so. The waveforms SUL in Fig. (6b ) shows the best case. On the other hand, this is not the case (SBL) for the bilateral rupture (B) from Syn51. Comparing the results for the two cases (U) and (B), it may be concluded that the unilateral case (U) in which the rupture spreads southwards from the northwestern periphery of the source region, appears to be more likely for the 2014 earthquake, unlike the case of the 2010 Maule event.
) shows the best case. On the other hand, this is not the case (SBL) for the bilateral rupture (B) from Syn51. Comparing the results for the two cases (U) and (B), it may be concluded that the unilateral case (U) in which the rupture spreads southwards from the northwestern periphery of the source region, appears to be more likely for the 2014 earthquake, unlike the case of the 2010 Maule event.
5. RESULTS AND DISCUSSION
As described in the previous section, we calculated synthetic waveforms to be observed at each four IMS stations, during two Chilean megathrust events, the 2010 Maule and 2014 Iquique earthquakes, respectively, incorporating their several probable source parameters, together with the standard atmospheric temperature structure up to a height of 220 km. The comparison between these synthetics and the corresponding low-frequency waveforms observed for gravity waves appears to provide satisfactory agreement, at least, for their initial time interval of about 22 min or so. There still remain, however, some discrepancies between their absolute amplitudes. There leaves a possibility that some of the discrepancy might be due to our inadequate estimate of the source parameters, including average vertical ground displacements and its time constants in adopted or assumed source models. Another possible reason might be attributed to prevailing atmospheric conditions during the time of these earthquakes which could be somewhat deviated from the adopted standard atmospheric model. For these possible reasons, we did not make further attempts to fit exactly the calculated amplitudes to their corresponding observations.
We would like to mention here that these are the fourth and fifth megathrust earthquakes, from which low-frequency atmospheric waves including gravity modes have been emitted, since the first, unusual observation after the 1964 Alaskan earthquake (Mw = 9.2) [16Bolt BA. Seismic air waves from the great Alaskan earthquake. Nature 1964; 202: 1095-6.
[http://dx.doi.org/10.1038/20211095a0] , 17Mikumo T. Atmospheric pressure waves and tectonic deformation associated with the Alaskan earthquake of March 28, 1964. J Geophys Res 1968; 73: 2009-25.
[http://dx.doi.org/10.1029/JB0i006p02009] ], the Sumatra-Andaman earthquake (Mw=9.2) [18Mikumo T, Shibutani T, Le Pichon A, et al. Low-frequency acoustic-gravity waves from coseismic vertical deformation associated with the 2004 Sumatra-Andaman earthquake (Mw=9.2). J Geophys Res 2008; 113: B12402.
[http://dx.doi.org/10.1029/2008JB005710] , 19Raveloson A, Wang R, Kind R, Ceranna L, Yuan X. Seismic and gravity signals from the source of the 2004 Indian Ocean Tsunami. Nat Hazards Earth Syst Sci 2012; 12: 287-94.], and the 2011 Off-Tohoku earthquake (Mw=9.0) [21Mikumo T, Garces M, Shibutani T, Morii W, Okawa T, Ishihara Y. Acoustic-gravity waves from the source region of the 2011 great Tohoku earthquake (Mw=9.0). J Geophys Res 2013; 118: 1534-45.
[http://dx.doi.org/10.1002/jgrb.50143] ].
It is to be noteworthy that the present 2010 Maule, and 2014 Iquique earthquakes in Chile, even with slightly smaller magnitudes of Mw = 8.8 and 8.2 as compared with the three previous megathrust earthquakes, appear to have also generated low-frequency gravity waves with somewhat smaller amplitudes that could propagate up to long distances. This is the reason why the two Chilean earthquakes in 2010 and 2014 also yielded quite large-scale uplift and subsidence of the sea bottom over a wide area in the Nazca-South America subduction zone.
Previous theoretical studies on Tsunami generation [28Kajiura K. Tsunami source, energy and directivity of wave radiation. Bull Earthq Res Inst Univ Tokyo 1970; 48: 835-69.] and numerical simulations [29Saito T, Furumura T. Three-dimensional simulation of Tsunami generation and propagation: Application to intraplate events. J Geophys Res 2009; 114: B02307.
[http://dx.doi.org/10.1029/2007JB005523] ] clearly show that if the wavelength of the sea-bottom deformation is much longer than the water depth and if the deformation takes place in a few minutes or so, then the swelling and depression of the sea-surface behaves almost exactly like the sea-bottom deformation. These conditions are met exactly in the source regions of the two great earthquakes off the western coast of South America mentioned here. The rapid change of the sea-surface could excite atmospheric disturbances just above it. For a part of land area, if extended to some part of the source region, the ground surface would provide more direct upward pressure increase into the air. In any case, the pressure perturbation of the air directly above it has been estimated as less than a few to several Pa or even less, if the density of the air near the sea or ground surface, ρ0 =1.193 x 10-3 gr/cm3, the sound velocity c0 =320 m/s near the ground surface, and also their dissipation effects during propagation are taken into account. The disturbances over a wide source region favor the condition that low-frequency atmospheric waves could be efficiently excited and propagated through the lower to middle atmosphere to long distances. The frequency response of the sensors used at most of microbarograph stations, particularly at IMS stations, however, drops rapidly towards lower frequencies. Nevertheless, it was barely successful to observe atmospheric gravity waves this time. It is hoped in the future that the response could extend to cover lower frequencies to be able to observe low-frequency acoustic and gravity waves to reveal the lower to upper atmospheric temperature structures as well as to discuss the source characteristics of large earthquakes from atmospheric pressure waves. For the above five megathrust earthquakes, there is a variety in their source dimension and the amount of vertical tectonic deformation depending on their dip angle of the fault plane. Nevertheless, the rise time of their vertical displacement, which is directly related to the amplitude and waveforms of acoustic-gravity waves, ranged between 1.5 and 3.5 min. This reflects partly the total rupture time of the entire fault plane, but might suggest the possible maximum time for tectonic deformation that could take place in subduction zones.
It is to be also mentioned here that after this Maule, Chile earthquake, Tsunami arrival has been reported at a number of seashore sites particularly along Chile, Peru, and Ecuador in South America [30National Tsunami Warning Center Bulletin. NOAA 2010.]. It has also been found that the Tsunami waves arrived at two IMS stations, Easter Islands and Marquesas Islands, both are located in southwestern Pacific region and included in Table (1). The Tsunami arrival was with a height of 0.35 - 0.18 m at 3 hours and a half later than the gravity waves, indicating the Tsunami speed in these cases was between 220 and 239 m/sec. This means that the acoustic arrival might be used as early warning for Tsunami arrival [20Arai N, Iwakuni M, Watada S, Imanishi Y, Murayama T, Nogami M. Atmospheric boundary waves excited by the Tsunami generation related to the 2011 great Tohoku-Oki earthquake. Geophys Res Lett 2011; 38: L00G18.
[http://dx.doi.org/10.1029/2011 GL049146] , 21Mikumo T, Garces M, Shibutani T, Morii W, Okawa T, Ishihara Y. Acoustic-gravity waves from the source region of the 2011 great Tohoku earthquake (Mw=9.0). J Geophys Res 2013; 118: 1534-45.
[http://dx.doi.org/10.1002/jgrb.50143] ], although the Tsunami amplitudes this time were not high enough to issue urgent warning at far-field stations. After the 2014 Iquique earthquake, on the other hand, Tsunami waves arrived at several sites within 4 hours along the western coast of Chile up to a height of 0.7 - 2.0 m [31Tohoku University. Modeling of the 2014 Chile Tsunami, Report of the NW of Iquique, Chile Tsunami of April 1 2014.].
CONCLUSION
Low-frequency atmospheric gravity waves have been recorded after two recent Chilean megathrust events, during 6.5 hours after the 2010 Maule (Mw8.8), and during 4.7 hours after the 2014 Iquique (Mw8.2) earthquakes, respectively, with apparent phase velocity of about 319 m/s and 337 m/s at several microbarograph stations in South America and its surrounding regions. To compare with these observations, we constructed synthetic waveforms to be recorded at these stations, incorporating seismic source characteristics of these earthquakes and a sound velocity structure up to a height of 220 km. The comparison suggests that the first part of these waves, at least, within 22 min have been actually excited by vertical tectonic deformation at the source regions of the two megathrust events, respectively. From this comparison, the time constant of the vertical deformation appears to be in the range between 2 and 3 min.
ETHICS APPROVAL AND CONSENT TO PARTICIPATE
Not applicable.
HUMAN AND ANIMAL RIGHTS
No Animals/Humans were used for studies that are base of this research.
CONSENT FOR PUBLICATION
Not applicable.
CONFLICT OF INTEREST
The authors declare no conflict of interest, financial or otherwise.
ACKNOWLEDGEMENTS
We thank the CTBTO for providing us with the IMS data obtained at their several stations. K. Heki suggested the first author to compare the acoustic-gravity waves from the Chilean earthquakes with those from the other three megathrust earthquakes. We are also grateful to M. Moreno for providing us with Table S2 in their paper showing the postseismic vertical deformation data obtained from their GPS measurements. We thank K. Obara for several comments on our preliminary manuscript and Y. Hoso for his technical assistance.
REFERENCES
| [1] | Lay T, Ammon CJ, Kanamori H, Koper KD, Sufri O, Hutko AR. Teleseismic inversion for rupture process of the 27 February 2010 Chile (Mw8.8) earthquake. Geophys Res Lett 2010; 37: L13301. [http://dx.doi.org/10.1029/2010GL043379] |
| [2] | Lay T, Yue H, Brodsky E, An C. The 1 April, 2014 Iquique Chile, Mw8.1 earthquake rupture sequence. Geophys Res Lett 2014; 41: 3818-25. [http://dx.doi.org/10,1002/2014GL060238] |
| [3] | Kiser E, Ishii M. The 2010 Mw8.8 Chile earthquake: Triggering on multiple segments and frequency dependent on rupture behavior. Geophys Res Lett 2011; 38: L07301. [http://dx.doi.org/10.1029/2011GL047140] |
| [4] | Pollitz F, Brooks B, Tong X, et al. Coseismic slip distribution of the February 27, 2010 Mw8.8 Maule, Chile earthquake. Geophys Res Lett 2011; 38: L09309 . [http://dx.doi.org/10.1029/2011GL047065] |
| [5] | Lorito S, Romano F, Atzori S, et al. Limited overlap between the seismic gap and coseismic slip of the great 2010 Chile earthquake. Nat Geosci 2011; 4: 173-7. [http://dx.doi.org/10.1038/ngeo1073] |
| [6] | Tong X, Sandwell D, Lutteri K, et al. The 2010 Maule, Chile earthquake: downdip rupture limit revealed by space geodesy. Geophys Res Lett 2010; 37: L24311. [http://dx.doi.org/10.1029/2010GL045805] |
| [7] | Faras M, Vargas G, Tassara A, et al. Land-level changes produced by the 2010 Mw8.8 Chile earthquake. Science 2010; 329: 916-20. [http://dx.doi.org/10.1126/science.1102094] |
| [8] | Vigny C, Socquet A, Peyrat S, et al. The 2010 Mw 8.8 Maule megathrust earthquake of central Chile, monitored by GPS. Science 2011; 332: 1417-21. [http://dx.doi.org/10.1126/science.1204132] |
| [9] | Heki K. A tale of two earthquakes. Science 2011; 332: 1390-1. |
| [10] | Moreno M, Melnik D, Rosenau M, et al. Toward understanding tectonic control on the Mw 8.8 2010 Maule, Chile earthquake. Earth Planet Sci Lett 2012; 321-322: 152-65. |
| [11] | Kelleher JA. Rupture zone of large South American earthquakes and some predictions. J Geophys Res 1972; 77: 2087-103. |
| [12] | Nishenko SP. Seismic potential for large and great interplate earthquakes along the Chilean and southern Peruvian margins of South America: a quantitative reappraisal. J Geophys Res 1985; 90: 3589-615. |
| [13] | Comite D, Pardo M. Reappraisal of great historical earthquakes in the northern Chile and southern Peru seismic gaps. Nat Hazards 1991; 4: 23-44. [http://dx.doi.org/10.1007/BF00126557] |
| [14] | An C, Sepulveda I, Liu PL. Tsunami source and its validation of the 2014 Iquique, Chile, earthquake. Geophys Res Lett 2014; 41: 3988-94. [http://dx.doi.org/10.1002/2014GL0650567] |
| [15] | Gusman AR, Murotani S, Satake K, et al. Fault slip distribution of the 2014 Iquique, Chile, earthquake estimated from ocean-wide Tsunami waveforms and GPS data. Geophys Res Lett 2015; 42: 1053-60. [http://dx.doi.org/10.1002/2014GL062604] |
| [16] | Bolt BA. Seismic air waves from the great Alaskan earthquake. Nature 1964; 202: 1095-6. [http://dx.doi.org/10.1038/20211095a0] |
| [17] | Mikumo T. Atmospheric pressure waves and tectonic deformation associated with the Alaskan earthquake of March 28, 1964. J Geophys Res 1968; 73: 2009-25. [http://dx.doi.org/10.1029/JB0i006p02009] |
| [18] | Mikumo T, Shibutani T, Le Pichon A, et al. Low-frequency acoustic-gravity waves from coseismic vertical deformation associated with the 2004 Sumatra-Andaman earthquake (Mw=9.2). J Geophys Res 2008; 113: B12402. [http://dx.doi.org/10.1029/2008JB005710] |
| [19] | Raveloson A, Wang R, Kind R, Ceranna L, Yuan X. Seismic and gravity signals from the source of the 2004 Indian Ocean Tsunami. Nat Hazards Earth Syst Sci 2012; 12: 287-94. |
| [20] | Arai N, Iwakuni M, Watada S, Imanishi Y, Murayama T, Nogami M. Atmospheric boundary waves excited by the Tsunami generation related to the 2011 great Tohoku-Oki earthquake. Geophys Res Lett 2011; 38: L00G18. [http://dx.doi.org/10.1029/2011 GL049146] |
| [21] | Mikumo T, Garces M, Shibutani T, Morii W, Okawa T, Ishihara Y. Acoustic-gravity waves from the source region of the 2011 great Tohoku earthquake (Mw=9.0). J Geophys Res 2013; 118: 1534-45. [http://dx.doi.org/10.1002/jgrb.50143] |
| [22] | Harkrider DG. Theoretical and observed acoustic-gravity waves from explosive sources in the atmosphere. J Geophys Res 1964; 69: 5295-321. [http://dx.doi.org/10.1029] |
| [23] | Yeh KC, Liu C. Acoustic-gravity waves in the upper atmosphere. Rev Geophys Space Phys 1974; 12: 193-216. |
| [24] | Hedin AE. Extension of the MSIS thermospheric model into middle and lower atmosphere. J Geophys Res 1991; 69: 1159-72. |
| [25] | Drob DP, Picone M, Garces MA. The global morphology of infrasound propagation. Geophys Res Lett 2003; 108: 4680. [http://dx.doi.org/10.1029/2002JD003307] |
| [26] | Press F, Harkrider DG. Propagation of acoustic-gravity waves in the atmosphere J Geophys Res 1962; 67: 3889-939. [http://dx.doi.org/10.1029/JZ 67i010p03889] |
| [27] | Pefffer RI, Zarichny J. Acoustic-gravity wave propagation in the atmosphere with two sound channels. Pure Appl Geophys 1963; 55: 175-99. |
| [28] | Kajiura K. Tsunami source, energy and directivity of wave radiation. Bull Earthq Res Inst Univ Tokyo 1970; 48: 835-69. |
| [29] | Saito T, Furumura T. Three-dimensional simulation of Tsunami generation and propagation: Application to intraplate events. J Geophys Res 2009; 114: B02307. [http://dx.doi.org/10.1029/2007JB005523] |
| [30] | National Tsunami Warning Center Bulletin. NOAA 2010. |
| [31] | Tohoku University. Modeling of the 2014 Chile Tsunami, Report of the NW of Iquique, Chile Tsunami of April 1 2014. |
Endorsements
Browse Contents
Table of Contents
- INTRODUCTION
- OBSERVATIONS OF PROPAGATING ATMOSPHERIC WAVES The next step is to compare above filtered channels at each station with the synthetic waveforms given in Section 4, in order to discuss the source characteristics of the above two megathrust earthquakes, after estimating approximate propagation phase velocity of the gravity waves radiated from these events.
- WAVEFORM MODELING
- COMPARISON BETWEEN THE OBSERVED AND SYNTHETIC WAVEFORMS
- RESULTS AND DISCUSSION
- CONCLUSION