The Open Condensed Matter Physics Journal




(Discontinued)

ISSN: 1874-1924 ― Volume 4, 2013

Electronic Structure of AlP Under Pressure Using Semiempirical Method



Hamad R. Jappor1, Mudar A. Abdulsattar2, Ahmed M. Abdul-lettif 3, *
1 College of Education, University of Babylon, Hilla, Iraq
2 Ministry of Science and Technology, Baghdad, Iraq
3 College of Science, University of Babylon, Hilla, Iraq

Abstract

The effect of pressure on the structural and electronic parameters of zinc-blende aluminum phosphide crystal has been investigated using the large unit cell within the framework of complete neglect of differential overlap and the linear combination of atomic orbital approximation. Cohesive energy, indirect band gap, valence bandwidth, conduction bandwidth, bulk modulus, and valence charge distribution are all obtained. The calculations show a good agreement of lattice constant, cohesive energy, valence bandwidth, and bulk modulus with the experimental data. The calculated band gap is twice the experimental value. This high value of the band gap is expected in Hartree-Fock method. The effect of pressure on the aforementioned properties is investigated. It is found that the indirect band gap, valence bandwidth, bulk modulus and cohesive energy increase with increasing pressure, while the conduction bandwidth decreases. The maximum value of pressure is taken to be 9 GPa, because beyond this value, the phase of AlP transforms from zinc blende phase to nickel arsenic phase.

PACS: 71.10-w, 71.15-m, 71.15. Ap, 71.15. Nc, 64.10.+h.

Keywords: Pressure, band structure, AlP, semiempirical, LUC, CNDO.

Article Information


Identifiers and Pagination:

Year: 2010
Volume: 3
First Page: 1
Last Page: 7
Publisher Id: TOCMPJ-3-1
DOI: 10.2174/1874186X01003010001

Article History:

Received Date: 21/8/2009
Revision Received Date: 11/10/2009
Acceptance Date: 28/10/2009
Electronic publication date: 4/3/2010

© Jappor et al.; Licensee Bentham Open.

open-access license: This is an open access article distributed under the terms of the Creative Commons Attribution License (http://creativecommons.org/licenses/by-nc/3.0/), which permits unrestrictive use, distribution, and reproduction in any medium, provided the original work is properly cited.


* Address correspondence to this author at the College of Science, University of Babylon, Hilla, Iraq; Tel: 009647801106357; E-mail: abdullettif@yahoo.com



1. INTRODUCTION

Aluminum phosphide (AlP) is a wide-indirect band gap semiconductor. At normal conditions, AlP crystallizes in the zinc-blende (zb) structure [1]. High-pressure experiments on this compound are difficult because of sample handling problems; AlP is unstable in air [2]. The zb form has been reported theoretically to be metastable. The zinc- blende phase is known to transform to the nickel arsenic (NiAs) phase at about ((17 – 9.5 GPa [3]. Although other studies have placed this transformation at a somewhat smaller pressure (7 - 9.3) GPa [4]. At a pressure of about 36 GPa the NiAs phase has been reported to undergo a Cmcm–like distortion with no significant change in volume. The CsCl phase is a possible candidate for AlP at very high pressures [2]. AlP is a subject of extensive theoretical studies ranging from the semiempirical to the first principles methods [5] within the density functional theory (DFT) framework using both pseudopotential [2], and all-electron approaches. For the bulk phase of AlP, theoretical calculations based on the Hartree-Fock [6], and potential model [7] have obtained a very good description of its structural and electronic properties.

Over the last few years, the study of materials under high pressure has become an extremely important subject. This is primarily due to both theoretical and experimental developments, which have facilitated such work [8].

The pressure is a continuously varying parameter that can be used in systematic studies of the properties of solids as a function of interatomic distances. An interesting phenomenon that may occur at the applied pressure is a sudden change in the arrangement of the atoms, i.e., a structural phase transition of atomic arrangement. The ultimate pressures in the experiment can lead to a reduction in the volume by a factor of two causing enormous changes in the inter-atomic bonding [9].

In the present work we study the band structure and some physical properties of cubic AlP under pressure using large unit cell method within complete neglect of differential overlap (LUC-CNDO) method [10, 11]. This method has been chosen in the present work rather than other methods because this can be used to give reliable and precise results with relatively short time.

2. CALCULATIONS

We have used the large unit cell within complete neglect of differential overlap (LUC-CNDO) method in the linear combination of atomic orbital (LCAO) approximation [10] to obtain a self-consistent solution for the valence electron energy spectrum. The iteration process was repeated until the calculated total energy of crystal converged to less than 1meV. The calculations are carried out, on the 8-atom LUC. The positions of atoms that constitute this LUC are calculated in the program according to the zinc-blende structure for a given lattice constant. There are four electrons in average per each atom. Hence we have (32) eigenstates, two electrons per state, half are filled (valence band) leaving the other half empty (conduction band) in the ground state. We obtained the energy minima against lattice constant variation.

The basic idea of the large unit cell is in computing the electronic structure of the unit cell extended in a special manner at k=0 in the reduced Brillouin zone (k is the lattice wave vector). Using the linear combination of atomic orbitals LCAO, the crystal wavefunction in the LUC-CNDO formalism is written in the following form [12]:


(1) 

where Cpa are the orbital expansion coefficients, the Ru is the lattice translation vector, and r is a position vector. The atomic orbitals used for the LCAO procedure form the basis set of the calculation. We expand the wave function in a set of Slater-type orbitals (STO), that have the radial form [13]:


(2) 

where ζ the orbital exponent. The expectation value of the electronic energy is:


(3) 

The Hamiltonian for a microcrystal consisting of N electrons may be written as:


(4) 

where ZA is the core charge, RAB is the distance between the atoms A and B, and the summation is over all nuclei. The Roothaan-Hall equations can be obtained [14]:


(5) 

Fpqk represents the Fock matrix elements. Spq is the overlap integral for atomic function Φq and ΦP, and can be written as [12]:


(6) 

The Fock matrix elements may represent the sum of the one- and two- electron components:


(7) 

is the density element with the form:


(8) 

In equation (5) if k =0 then


(9) 

The Fock matrix elements in their final forms in the LUC-CNDO formalism are used in this work to be [11]:


(10) 

(11) 

For p and q on the same atomic center, βAB is the bonding parameter and (AB is the average electrostatic repulsion between any electron on atom A and any electron on atom B, and can be written as


(12) 

Ip and AP are the ionization potential and electron affinity respectively, and f(x) is the modulating function that is given by [15]


(13) 

For the eight atoms LUC x is given by


(14) 

RAB is the distance between the atom A at the central lattice o and the atom B at the v lattice.

In our calculations, we have treated only valence orbitals of Al (3s23p1) and P (3s23p3). The coordinates of the P atoms are chosen to be (0, 0, 0); (0, 1/2, 1/2); (1/2, 0, 1/2); (1/2, 1/2, 0) whereas the coordinates of the Al atoms are chosen to be (1/4, 1/4, 1/4); (1/4, 3/4, 3/4); (3/4, 1/4, 3/4); (3/4, 3/4, 1/4).

3. RESULTS AND DISCUSSION

3.1. Choice of Parameters

The number of parameters in the LUC–CNDO method is four. These are the orbital exponent (ζ), the bonding parameter (β), the electronegativity of s-orbital (Es), and the electronegativity of p-orbital (Ep). The value of the orbital exponent determines the charge distribution of electrons around the nucleus in the solid

These parameters are varied firstly to give nearly an exact value of the equilibrium lattice constant, cohesive energy, indirect bandgap and valence bandwidth. The remaining of the output data of the programs is a result of the theory that is used in the present work. We found that the investigated properties are sensitive to the aforementioned parameters. The parameters used for AlP in the present work are summarized in Table 1.

Table 1

The Adjusted Parameters for AlP in the Zinc-Blende Structure




3.2. The Electronic and Structural Properties

The second step after the choice of parameters is to examine the structural properties of AlP at the equilibrium lattice constant in order to test the accuracy of the cohesive energy, indirect bandgap, and valence bandwidth.

Based on the total energy result, we obtained the cohesive energy (Ecoh) as follows:


(15)  Ecoh=Etot/8-Efree-E0

where Etot is the total energy, Efree is the free atom sp shell energy, and E0 is the zero–point vibration energy. In the present work Efree =115.045eV, and this value is taken from the ionization potential of AlP, E0= 0.057 eV, is calculated by the formula E0= (9/8)kВ θ D (per atom) with θ D is the Debye temperature [16], which is equal to 588 K [17].

The present value of the cohesive energy is in good agreement with the experimental and other calculations [16,18,19] as shown in Table 2. Fig. (1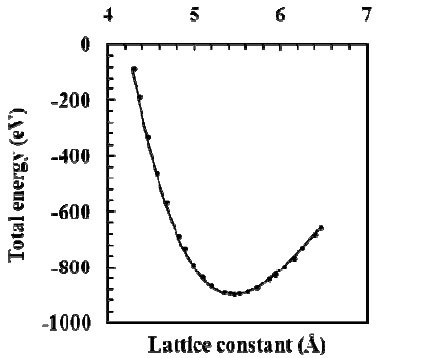) displays the total energy versus the lattice constant for AlP. The curve is fitted to the equation of state of Murnaghan [20] from which we obtained the equilibrium lattice parameter (a0), the bulk modulus B and its derivative B(O, and the cohesive energy as listed in Table 2.

Fig. (1)

The total energy as a function of lattice constant for AlP.


Table 2

Structural Properties of zb-AlP at Zero Pressure Determined by LUC-CNDO Compared to other Theoretical Calculations and Experimental Data




The calculated structural properties of AlP, in comparison with experimental results and other computational results, are shown in Table 2. We notice that the lattice parameter for the zb of AlP of 5.453Å is in good agreement with the experimental value of 5.451 Å [6] with an accuracy of 0.04%. For the bulk modulus, the accuracy is about 0.2 %. Table 2 shows that the calculated value of is in fair agreement with the previous computational [4, 19] and experimental [18] results.

To visualize the nature of the bond character and to explain the charge transfer and the bonding properties of zb-AlP, we calculate the total charge density. The total valence charge densities for AlP are displayed along the Al-P bonds in the (100), (110), (200), and (400) planes in Fig. (2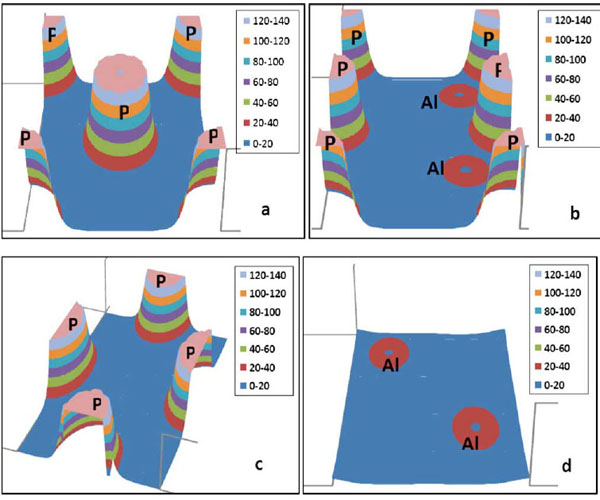). From this figure, it is apparent that the phosphorous ions are larger than the aluminum ions. This figure also shows the charge density accumulated at the P site. Fig. (2a) shows the charge density of the (100) plane, where a buildup of charge density along the AlP bond on the plane is clearly visible. This figure reveals that LUC-CNDO calculations give a reasonable description of the partially ionic bonding character in regions between atoms of different affinities.

Fig. (2)

The valence charge density (in electron/Å3) of zb-AlP at zero pressure in (a) (100) plane, (b) (110) plane, (c) (200) plane, and (d) (400) plane.


3.3. The Band Structure and Energy Eigenvalues

The electronic band structure of a solid shows the eigenvalues associated with the valence and conduction bands along specific directions in the Brillouin zone. We will start our discussion of calculations on the band structure by the energy eigenvalues for AlP crystal at various high symmetry points of the Brillouin zone. The results are listed in Table 3>. Eight atom LUC results Г and Χ points of the FCC Brillouin zone. They are the valence band states Г1v, Г15v, X1v, and X5v, and the conduction band states X1c, X5c, Г15c, and Г1c.

The direct bandgap in the zb structures of AlP is due to the Al 3s and P 3s orbital interaction, which forms the lower-energy bonding state (Γ15v) and the antibonding state (Γ1c). The bonding state is lowered and antibonding states is risen, relative to the P 3s and Al 3s orbital energies, by the same amount of s-s interaction energy in AlP. In zb-AlP the conduction-band minimum (CBM) is located away from the Γ point, at the X point. AlP has an indirect minimum gap with the CBM at X. Thus, we obtain an indirect bandgap (Egind) of 6.6075 eV which is larger than the results of others [21, 22] (see Table 4 for comparison), this is, mainly, a consequence of two approximations made in the present calculations. First, the core structure was ignored, through some compensation results from using semiempirical parameters. Second, using minimal basis set atomic orbitals (without considering any excited levels). However, the CNDO method predicts a one-electron eigenvalue band gap that is too large and conduction band that is much narrower than the band model values.

Table 3

Eigenvalues (in Electron Volts) at Г and Χ High-Symmetry Points of Brillouin Zone




The total valence bandwidth (VBW) or the difference between the top of the valence band (Γ15v) and the lowest energy of valence band (Γ1v) is 13.492 eV for zb-AlP. The obtained total valence bandwidth is in fair agreement with previous results as shown in Table 4. The maximum level of the valence band is splitted only by spin-orbit interaction Δso, giving rise to two states at the Brillouin zone centre: Γ8v and Γ7v. In the absence of spin orbit splitting, these levels become a triply degenerated Γ15v. The spin-orbit interaction Δso is taken into account in this paper, averaging the theoretical results from different Refs. to be 0.06eV [21, 23, 24]. Therefore, we added the relativistic correction to the band gap, which is equal to 0.019 [23]. Our work gives a value of the conduction bandwidth (CBW) to be 14.728 eV (Table 4), but no experimental results are found to the CBW of the zb of AlP.

Table 4

Calculated LUC-CNDO Indirect Band Gap, Valence Bandwidth, and Conduction Bandwidth of AlP Compared to other Theoretical Calculations and Experiments. All Energies are in eV




4. THE EFFECT OF PRESSURE ON THE PHYSICAL PROPERTIES

The effect of pressure on the electronic structure and other properties can be calculated from the present computational procedure. By the use of our calculated values of the bulk modulus B and its derivative B(O, the volume change (V) with applied pressure was calculated using the following equation [26]:


(16) 

P is the pressure and V0 is the equilibrium volume at zero pressure. We use pressures up to 9 GPa, because this structure transforms to another phase, the nickel arsenic phase (NiAs), when pressure exceeds nearly 9 GPa [27]. The calculated lattice constant as a function of pressure is shown in Fig. (3).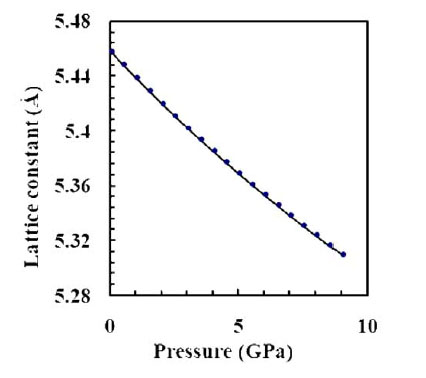

Fig. (3)

The effect of pressure on the lattice constant of AlP.


The pressure dependence of the bulk modulus and the cohesive energy is illustrated in Figs. (4 and 5), respectively. It is shown that the bulk modulus increases linearly with the pressure. On the other hand, the absolute value of the cohesive energy decreases as the pressure increases.

Fig. (4)

The bulk modulus as a function of pressure for AlP.


Fig. (5)

The bulk modulus as a function of pressure for AlP.


The effect of pressure on the lattice constant of AlP.

The effect of pressure on the high symmetry points (Г1v , Г15v , X1v , X5v , X1c, X5c, Г15c, and Г1c) is shown in Fig. (6). From this figure one can notice that the eigenvalues at conduction band (X5c , Г15c , Г1c , X1c) increase with pressure, whereas eigenvalues at valence band (X5v , X1v , Г1v ) decrease with pressure, However, the decrease of X5v , X1v , and Г1v with pressure is small.

Fig. (6)

The effect of pressure on the high symmetry points in the (a) conduction band (X5c , Г 15c , Г 1c , X1c) , and (b) valence band (X5v , X1v , Г1v ).


Fig. (7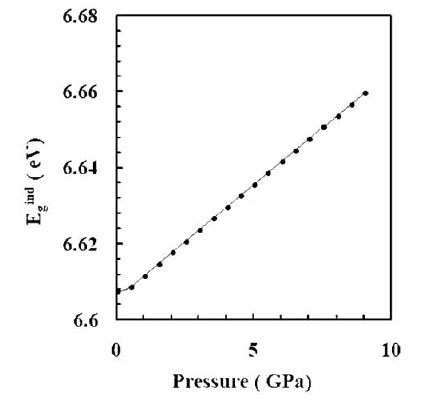) shows the pressure dependence of the indirect band gap of the zb phase of AlP from the present energy band structure calculations. The indirect bandgap increases with the increase of pressure; because the minimum conduction energy level rises and the top valence energy level lowers with the increase of pressure. However, in most cases the first pressure-induced phase transition corresponds to the closing of the bandgap and metallization of the sample. In the present work, the pressure derivative of the indirect bandgap is computed to be ~ 4.2 meV/GPa.

Fig. (7)

The effect of pressure on the high symmetry points in the (a) conduction band (X5c , Г 15c , Г 1c , X1c) , and (b) valence band (X5v , X1v , Г1v ).


The predicted effect of pressure on the conduction bandwidth and valence bandwidth is illustrated in Fig. (8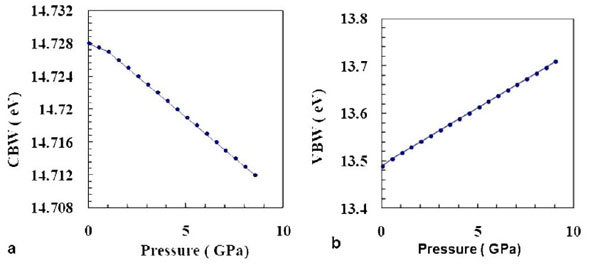). The conduction bandwidth decreases with the increase of pressure, while the valence bandwidth increases with the increase of pressure. Our calculations give a pressure derivative of ~ -1.9 meV/GPa for the conduction bandwidth, and 22 meV/GPa for the valence bandwidth.

Fig. (8)

Effect of pressure on the (a) conduction bandwidth, and (b) valence bandwidth.


5. CONCLUSIONS

In this paper, a study of some properties of AlP is presented. The cohesive energy, lattice constant, bulk modulus, and its pressure derivative have been calculated by (LUC-CNDO) method. The calculated results indicate that this model gives results in good agreement with the corresponding experimental results, and this shows the possibility of using this model in qualitative study of some materials. The LUC-CNDO method is shown to be time efficient and retains many of the essential features of ab initio Hartree-Fock theory. A reasonable agreement of the valence bandwidth is shown in comparison with the available theoretical result. However, there is a large difference between the calculated indirect band gap and the corresponding experimental value. The effect of pressure on these properties is investigated. It is found that the conduction bandwidth decreases with increasing the pressure, whereas the indirect bandgap, valence bandwidth, and cohesive energy increase with the increase of pressure. The maximum value of pressure is taken to be 9 GPa, because beyond this value of pressure, the phase of AlP transforms from zb to rock salt phase. Relativistic effect is added to the calculation of the band gap, also zero point energy is added to the calculation of the cohesive energy. Finally, this model is shown to give a good description to the charge density of AlP and it is expected that this method could give reliable description for other materials that have zinc blende and cubic structures.

REFERENCES
Track Your Manuscript:


Endorsements



"Open access will revolutionize 21st century knowledge work and accelerate the diffusion of ideas and evidence that support just in time learning and the evolution of thinking in a number of disciplines."


Daniel Pesut
(Indiana University School of Nursing, USA)

"It is important that students and researchers from all over the world can have easy access to relevant, high-standard and timely scientific information. This is exactly what Open Access Journals provide and this is the reason why I support this endeavor."


Jacques Descotes
(Centre Antipoison-Centre de Pharmacovigilance, France)

"Publishing research articles is the key for future scientific progress. Open Access publishing is therefore of utmost importance for wider dissemination of information, and will help serving the best interest of the scientific community."


Patrice Talaga
(UCB S.A., Belgium)

"Open access journals are a novel concept in the medical literature. They offer accessible information to a wide variety of individuals, including physicians, medical students, clinical investigators, and the general public. They are an outstanding source of medical and scientific information."


Jeffrey M. Weinberg
(St. Luke's-Roosevelt Hospital Center, USA)

"Open access journals are extremely useful for graduate students, investigators and all other interested persons to read important scientific articles and subscribe scientific journals. Indeed, the research articles span a wide range of area and of high quality. This is specially a must for researchers belonging to institutions with limited library facility and funding to subscribe scientific journals."


Debomoy K. Lahiri
(Indiana University School of Medicine, USA)

"Open access journals represent a major break-through in publishing. They provide easy access to the latest research on a wide variety of issues. Relevant and timely articles are made available in a fraction of the time taken by more conventional publishers. Articles are of uniformly high quality and written by the world's leading authorities."


Robert Looney
(Naval Postgraduate School, USA)

"Open access journals have transformed the way scientific data is published and disseminated: particularly, whilst ensuring a high quality standard and transparency in the editorial process, they have increased the access to the scientific literature by those researchers that have limited library support or that are working on small budgets."


Richard Reithinger
(Westat, USA)

"Not only do open access journals greatly improve the access to high quality information for scientists in the developing world, it also provides extra exposure for our papers."


J. Ferwerda
(University of Oxford, UK)

"Open Access 'Chemistry' Journals allow the dissemination of knowledge at your finger tips without paying for the scientific content."


Sean L. Kitson
(Almac Sciences, Northern Ireland)

"In principle, all scientific journals should have open access, as should be science itself. Open access journals are very helpful for students, researchers and the general public including people from institutions which do not have library or cannot afford to subscribe scientific journals. The articles are high standard and cover a wide area."


Hubert Wolterbeek
(Delft University of Technology, The Netherlands)

"The widest possible diffusion of information is critical for the advancement of science. In this perspective, open access journals are instrumental in fostering researches and achievements."


Alessandro Laviano
(Sapienza - University of Rome, Italy)

"Open access journals are very useful for all scientists as they can have quick information in the different fields of science."


Philippe Hernigou
(Paris University, France)

"There are many scientists who can not afford the rather expensive subscriptions to scientific journals. Open access journals offer a good alternative for free access to good quality scientific information."


Fidel Toldrá
(Instituto de Agroquimica y Tecnologia de Alimentos, Spain)

"Open access journals have become a fundamental tool for students, researchers, patients and the general public. Many people from institutions which do not have library or cannot afford to subscribe scientific journals benefit of them on a daily basis. The articles are among the best and cover most scientific areas."


M. Bendandi
(University Clinic of Navarre, Spain)

"These journals provide researchers with a platform for rapid, open access scientific communication. The articles are of high quality and broad scope."


Peter Chiba
(University of Vienna, Austria)

"Open access journals are probably one of the most important contributions to promote and diffuse science worldwide."


Jaime Sampaio
(University of Trás-os-Montes e Alto Douro, Portugal)

"Open access journals make up a new and rather revolutionary way to scientific publication. This option opens several quite interesting possibilities to disseminate openly and freely new knowledge and even to facilitate interpersonal communication among scientists."


Eduardo A. Castro
(INIFTA, Argentina)

"Open access journals are freely available online throughout the world, for you to read, download, copy, distribute, and use. The articles published in the open access journals are high quality and cover a wide range of fields."


Kenji Hashimoto
(Chiba University, Japan)

"Open Access journals offer an innovative and efficient way of publication for academics and professionals in a wide range of disciplines. The papers published are of high quality after rigorous peer review and they are Indexed in: major international databases. I read Open Access journals to keep abreast of the recent development in my field of study."


Daniel Shek
(Chinese University of Hong Kong, Hong Kong)

"It is a modern trend for publishers to establish open access journals. Researchers, faculty members, and students will be greatly benefited by the new journals of Bentham Science Publishers Ltd. in this category."


Jih Ru Hwu
(National Central University, Taiwan)

Browse Contents




Webmaster Contact: info@benthamopen.net
Copyright © 2023 Bentham Open