- Home
- About Journals
-
Information for Authors/ReviewersEditorial Policies
Publication Fee
Publication Cycle - Process Flowchart
Online Manuscript Submission and Tracking System
Publishing Ethics and Rectitude
Authorship
Author Benefits
Reviewer Guidelines
Guest Editor Guidelines
Peer Review Workflow
Quick Track Option
Copyediting Services
Bentham Open Membership
Bentham Open Advisory Board
Archiving Policies
Fabricating and Stating False Information
Post Publication Discussions and Corrections
Editorial Management
Advertise With Us
Funding Agencies
Rate List
Kudos
General FAQs
Special Fee Waivers and Discounts
- Contact
- Help
- About Us
- Search

The Open Mathematics, Statistics and Probability Journal
The Open Statistics & Probability Journal
(Discontinued)
ISSN: 2666-1489 ― Volume 10, 2020
A New Class of Distributions Based on Hurwitz Zeta Function with Applications for Risk Management
Zinoviy Landsman, Udi Makov, Tomer Shushi*
Abstract
This paper constructs a new family of distributions, which is based on the Hurwitz zeta function, which includes novel distributions as well important known distributions such as the normal, gamma, Weibull, Maxwell-Boltzmann and the exponential power distributions. We provide the n-th moment, the Esscher transform and premium and the tail conditional moments for this family.
Article Information
Identifiers and Pagination:
Year: 2016Volume: 7
First Page: 53
Last Page: 62
Publisher Id: TOSPJ-7-53
DOI: 10.2174/1876527001607010053
Article History:
Received Date: 17/08/2016Revision Received Date: 31/08/2016
Acceptance Date: 01/09/2016
Electronic publication date: 27/12/2016
Collection year: 2016
open-access license: This is an open access article licensed under the terms of the Creative Commons Attribution-Non-Commercial 4.0 International Public License (CC BY-NC 4.0) (https://creativecommons.org/licenses/by-nc/4.0/legalcode), which permits unrestricted, non-commercial use, distribution and reproduction in any medium, provided the work is properly cited.
* Address correspondence to this author at the Department of Statistics, University of Haifa, Mount Carmel, 31905, Haifa, Israel; Tel: +97254593134; E-mail: tomershushi@gmail.com
| Open Peer Review Details | |||
|---|---|---|---|
| Manuscript submitted on 17-08-2016 |
Original Manuscript | A New Class of Distributions Based on Hurwitz Zeta Function with Applications for Risk Management | |
1. INTRODUCTION
The Hurwitz Zeta function, which was introduced by Hurwitz (1882) (see for instance Espinosa and Victor (2002) [1O. Espinosa, and H.M. Victor, "On some integrals involving the Hurwitz Zeta function: Part 1", Ramanujan J., vol. 6, no. 2, pp. 159-188, 2002.
[http://dx.doi.org/10.1023/A:1015706300169] ]), is a generalization of the Riemann Zeta function defined as follows:
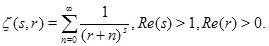 |
(1) |
Notice that the Riemann Zeta function is simply ζ(s, 1) = ζ(s).
In the next section we provide a new family of distributions, the Zeta family, which is based on the Hurwitz Zeta function, and provide its characteristic function. We also show that the well known generalized gamma family of distributions is a special case of the proposed family. (Notice that the exponential power family of distributions, the gamma, Weibull, Maxwell-Boltzmann and chi-squared distributions are special cases of the GG family). In section 3 we derive the Esscher transform and premium, and in section 4 we provide the tail conditional moments and the tail conditional expectation for members of this family. A conclusion is provided in section 5.
2. A NEW CLASS OF DISTRIBUTIONS
Let us consider the following important integral representation ζ(s, r) (see [1O. Espinosa, and H.M. Victor, "On some integrals involving the Hurwitz Zeta function: Part 1", Ramanujan J., vol. 6, no. 2, pp. 159-188, 2002.
[http://dx.doi.org/10.1023/A:1015706300169] ])
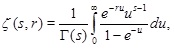 |
(2) |
for real s, r where s > 1, r > 0.
Theorem 1. The function
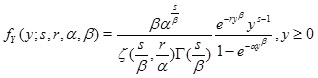 |
(3) |
is a probability density function (pdf), the Zeta density, with parameters r, α, β > 0 and s > β.
Proof. Using (2) we have
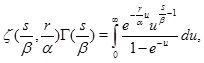 |
after transformation u = αtβ we immediately get
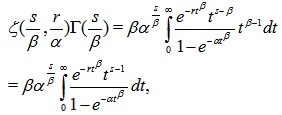 |
then it is clear that fY(y;s,r,α,β) is a pdf.
Notice that we can calculate Hurwitz zeta effortlessly, using common mathematical packages such as Mathematica, where the function Zeta[s, r] can be calculated once the values of s and r are specified.
The Zeta and GG families of distributions shares some famous special cases such as the exponential power, normal, gamma, Weibull, Rayleigh, Maxwell-Boltzmann and chi-squared distributions (see Landsman and Valdez (2003) [2Z.M. Landsman, and E.A. Valdez, "Tail conditional expectations for elliptical distributions", N. Am. Actuar. J., vol. 7, no. 4, pp. 55-71, 2003.
[http://dx.doi.org/10.1080/10920277.2003.10596118] ] for the exponential power family of distributions and Christensen (1984) [3R. Christensen, Data Distributions: A Statistical Handbook., Entropy Limited, 1984.] pages (21, 149, 175, 160, 161, 147) for the other distributions, respectively). However, there are additional models which belongs to the proposed family of distributions but which are not members of the GG family. From the great variety of models, examples of seven such models are given in Table 1.
In Figs. (1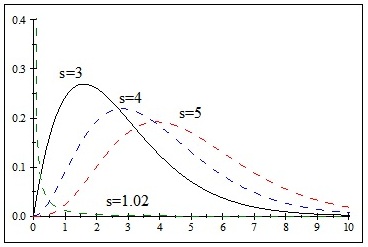 ) and (2
) and (2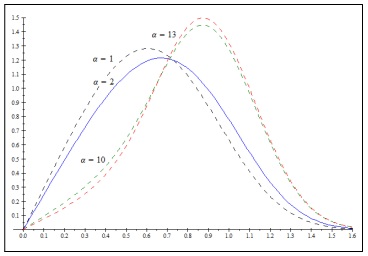 ) we notice that as the values of s and α respectively, are getting larger the right tail of the distribution is getting heavier. For Figs. (3
) we notice that as the values of s and α respectively, are getting larger the right tail of the distribution is getting heavier. For Figs. (3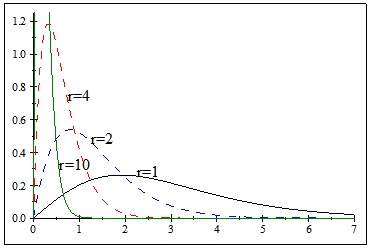 ) and (4
) and (4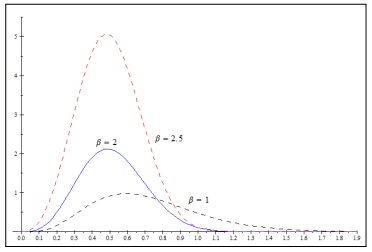 ) we see that as r and β are getting larger the right tails of the distributions are getting thinner.
) we see that as r and β are getting larger the right tails of the distributions are getting thinner.
 |
Fig. (1) Graph of the pdf (3) for r=α=β=1 and for various values of s (for s=3 this is model 1). |
 |
Fig. (2) Graph of the pdf (3) for s=5, r=2, β=3 and for various values of α (for α=2 this is model 2). |
 |
Fig. (3) Graph of the pdf (3) for s=3, α=2, β=1 and for various values of r (for r=10 this is model 3). |
 |
Fig. (4) Graph of the pdf (3) for s=6, r=8, α=4 and for various values of β (for β=2 this is model 4). |
We now establish properties of the Zeta family.
Corollary 1. The nth moment of Y with the pdf (3) has the following form
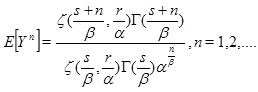 |
(4) |
Proof. Using (2), the nth moment of Y is derived as follows:
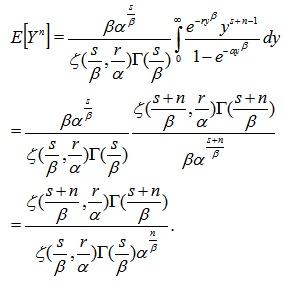 |
Remark 1. Using common mathematical packages such as Mathematica, we can calculate the moments of the zeta family immediately using the Hurwitz zeta function N[Zeta[s,r],n] and the gamma functionN[Г(a),n]. The level of precision is controlled bynthe number of decimal places.
Corollary 2. The characteristic function of the pdf (3) takes the following form
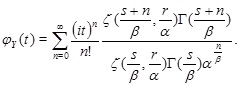 |
(5) |
Note that by differentiation of (5) with respect to t and substituting t = 0 we can easily calculate the moments of the zeta distribution explicitly.
Proof. Using the identity (2) we get
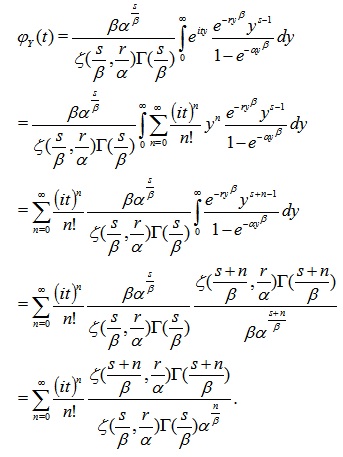 |
Corollary 3. The GG family of distributions takes the form of (3) for r = θ-β, θ > 0 and α → ∞
Proof. Using (3), we take the limit of the constant of the pdf with respect to α as follows:
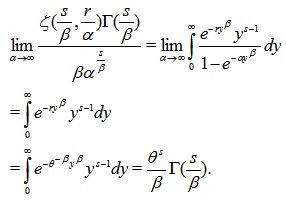 |
Then, applying this limit and substituting r = θ-β we immediately get
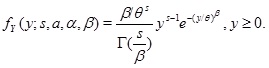 |
3. ESSCHER TRANSFORM AND PREMIUM
Esscher transform (ET), which takes the form
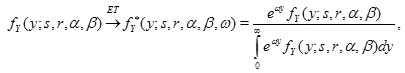 |
(6) |
is a proper tool in risk measurement and portfolio allocation (see, for instance, Landsman (2004) [4Z. Landsman, "On the generalization of Esscher and variance premiums modified for the elliptical family of distributions", Insur. Math. Econ., vol. 35, no. 3, pp. 563-579, 2004.
[http://dx.doi.org/10.1016/j.insmatheco.2004.07.006] ] and Bühlmann et al. (1998) [5H. Buhlmann, F. Delbaen, P. Embrechts, and A.N. Shiryaev, "On Esscher transforms in discrete finance models", ASTIN Bull., vol. 28, pp. 171-186, 1998.
[http://dx.doi.org/10.2143/AST.28.2.519064] ]).
Before we provide the ET for the Zeta family of distributions let us recall the generalized Hurwitz Zeta function which was introduced and studied in Raina and Chhajed (2004) [6R.K. Raina, and P.K. Chhajed, "Certain results involving a class of functions associated with the Hurwitz zeta function. Acta", Math. Univ. Comenianae, vol. 73, no. 1, pp. 89-100, 2004.], as follows:
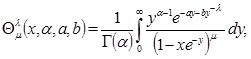 |
(7) |
where α, a, b ϵ C, µ ≥ 1, λ > 0, x ϵ R and Re(a) > 0, Re(b) > 0. In the case α > 0, x, µ = 1, and a > 1, the parameters b and λ can take negative values.
Remark 2. Using common mathematical Packages such as Mathematica, we can compute (7) by numerical integration procedures with accuracy of n digits. In the case of Mathematica we simply write
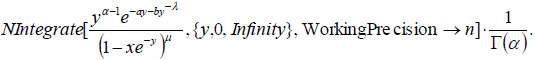 |
(8) |
Example 1. Using (8), forλ = -1/3, µ = 1, x = 1, α = 4, a = 2, b = -0.5 and under precision of 7 digits of the function (7) we get, in a split of a second,
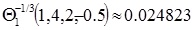 |
Theorem 2. Using (6), the ET of the Zeta family has the following form
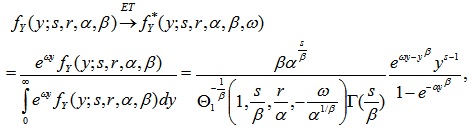 |
(9) |
where ω is a strictly positive parameter.
Proof. Using the form of Esscher transform (see [5H. Buhlmann, F. Delbaen, P. Embrechts, and A.N. Shiryaev, "On Esscher transforms in discrete finance models", ASTIN Bull., vol. 28, pp. 171-186, 1998.
[http://dx.doi.org/10.2143/AST.28.2.519064] ]) we write
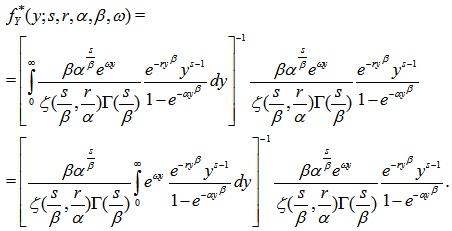 |
After introducing the transformation αyβ = u into the integral, we obtain
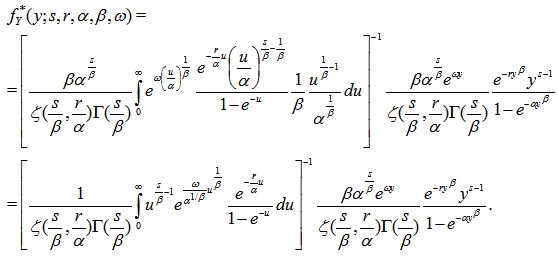 |
Now, using (7), it is clear that
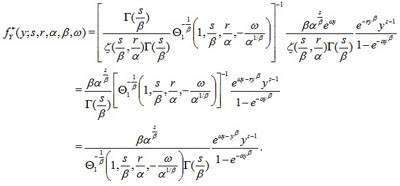 |
Esscher premium, which takes the form
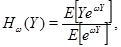 |
(10) |
is the expectation of a random variable Y with a pdf obtained by the Esscher transform f* This premium is interpreted as a pure loading premium for Y : f*(y)(see [4Z. Landsman, "On the generalization of Esscher and variance premiums modified for the elliptical family of distributions", Insur. Math. Econ., vol. 35, no. 3, pp. 563-579, 2004.
[http://dx.doi.org/10.1016/j.insmatheco.2004.07.006] ] and [5H. Buhlmann, F. Delbaen, P. Embrechts, and A.N. Shiryaev, "On Esscher transforms in discrete finance models", ASTIN Bull., vol. 28, pp. 171-186, 1998.
[http://dx.doi.org/10.2143/AST.28.2.519064] ]).
Theorem 3. The Esscher premium of the random variable Y with the pdf (3) is expressed as follows:
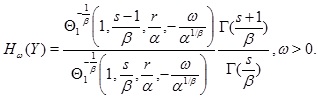 |
(11) |
Proof. By the definition of Esscher premium (see [4Z. Landsman, "On the generalization of Esscher and variance premiums modified for the elliptical family of distributions", Insur. Math. Econ., vol. 35, no. 3, pp. 563-579, 2004.
[http://dx.doi.org/10.1016/j.insmatheco.2004.07.006] ]) we write
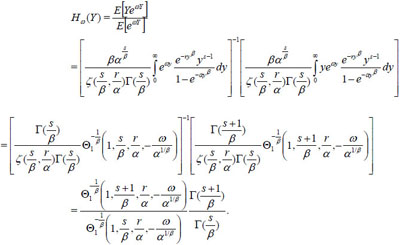 |
Remark 3. Notice that the Esscher premium of Y can be also expressed as follows
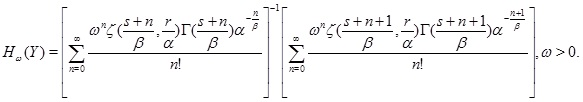 |
(12) |
(12) was derived by taking the series expansion of eωy and by considering the pdf (3).
4. TAIL CONDITIONAL MOMENTS FOR THE ZETA FAMILY
Risk management heavily relies on risk measures. The Tail Conditional Moments (TCM) are risk measures which includes the two important cases, the Tail Conditional Expectation (TCE) and the Tail Variance Premium (see Artzner et al. (1999) [7P. Artzner, "Coherent measures of risk", Math. Finance, vol. 9, pp. 203-228, 1999.
[http://dx.doi.org/10.1111/1467-9965.00068] ], Landsman and Valdez (2003) [2Z.M. Landsman, and E.A. Valdez, "Tail conditional expectations for elliptical distributions", N. Am. Actuar. J., vol. 7, no. 4, pp. 55-71, 2003.
[http://dx.doi.org/10.1080/10920277.2003.10596118] ], Furman and Landsman (2006) [8E. Furman, and Z. Landsman, "Tail variance premium with applications for elliptical portfolio of risks", Astin Bulletine, vol. 36, no. 2, pp. 433-462, 2006.
[http://dx.doi.org/10.2143/AST.36.2.2017929] ], and Landsman, Makov and Shushi (2013) [9Z.M. Landsman, U.E. Makov, and T. Shushi, "Tail conditional expectations for generalized skew elliptical distributions", SSRN http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2298265, Technical report., 2013.], and McDonald and Xu (2016) [10J.B. McDonald, and Y.J. Xu, "A generalization of the beta distribution with applications", J. Econom., vol. 66, no. 1, pp. 133-152, 1995.
[http://dx.doi.org/10.1016/0304-4076(94)01612-4] ]).
In this section we show how the TCM can be calculated for the Zeta family. First, we introduce the incomplete Hurwitz Zeta function as follows:
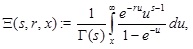 |
(13) |
where x ≥ 0. Notice that since we know that for x = 0 the function Ξ(s,r,x) is the Hurwitz zeta function, it is clear that Ξ(s,r,x) exists for any x ≥ 0. Notice that this function can be reduced to the sum of weighted incomplete gamma functions as follows
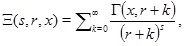 where
where
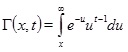 is the well known incomplete gamma function. We avoid calculating infinite sums by resorting to numerical integration as explained in the next remark.
is the well known incomplete gamma function. We avoid calculating infinite sums by resorting to numerical integration as explained in the next remark.
Remark 4. Notice that Ξ(s,r,x) can be calculated numerically (Such as Remark 2), with accuracy of n digits, by common mathematical packages. In the case of Mathematica we write
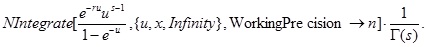 |
(14) |
Example 2. Using (14), for s = 5, r = 2, x = 2 and under precision of 7 digits of the function (13) we get, in a split of a second,
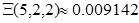 |
Theorem 4. The nth TCM of the Zeta family for quantileq ϵ (0,1) takes the form
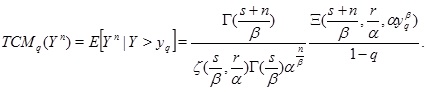 |
(15) |
Proof. Using (13) it is clear that
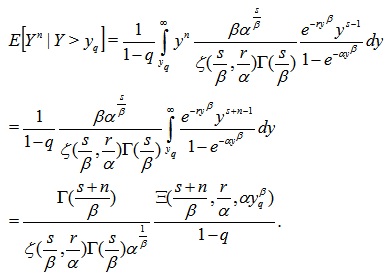 |
Corollary 4. The TCE of the Zeta family takes the form
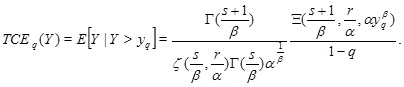 |
(16) |
Proof. The result follows from Theorem 3 for n = 1.
CONCLUSION
In this paper we derived the new Zeta family of distributions based on the well known Hurwitz Zeta function, which is a generalization of the Riemann Zeta function. The pdf of the family has the following form
 |
where s > α, and r, α, β > 0, and is shown to include the GG family. We further constructed the nth moment of this family, and provided additional properties of members of the family, including the Esscher premium and TCM.
We notice that this 4-parameter family is useful for statistical calibration of risk-management data, using, for example, the method of moments. However, this is beyond of the scope of the present paper.
CONFLICT OF INTEREST
The authors confirm that this article content has no conflict of interest.
ACKNOWLEDGEMENTS
Declared none.
REFERENCES
| [1] | O. Espinosa, and H.M. Victor, "On some integrals involving the Hurwitz Zeta function: Part 1", Ramanujan J., vol. 6, no. 2, pp. 159-188, 2002. [http://dx.doi.org/10.1023/A:1015706300169] |
| [2] | Z.M. Landsman, and E.A. Valdez, "Tail conditional expectations for elliptical distributions", N. Am. Actuar. J., vol. 7, no. 4, pp. 55-71, 2003. [http://dx.doi.org/10.1080/10920277.2003.10596118] |
| [3] | R. Christensen, Data Distributions: A Statistical Handbook., Entropy Limited, 1984. |
| [4] | Z. Landsman, "On the generalization of Esscher and variance premiums modified for the elliptical family of distributions", Insur. Math. Econ., vol. 35, no. 3, pp. 563-579, 2004. [http://dx.doi.org/10.1016/j.insmatheco.2004.07.006] |
| [5] | H. Buhlmann, F. Delbaen, P. Embrechts, and A.N. Shiryaev, "On Esscher transforms in discrete finance models", ASTIN Bull., vol. 28, pp. 171-186, 1998. [http://dx.doi.org/10.2143/AST.28.2.519064] |
| [6] | R.K. Raina, and P.K. Chhajed, "Certain results involving a class of functions associated with the Hurwitz zeta function. Acta", Math. Univ. Comenianae, vol. 73, no. 1, pp. 89-100, 2004. |
| [7] | P. Artzner, "Coherent measures of risk", Math. Finance, vol. 9, pp. 203-228, 1999. [http://dx.doi.org/10.1111/1467-9965.00068] |
| [8] | E. Furman, and Z. Landsman, "Tail variance premium with applications for elliptical portfolio of risks", Astin Bulletine, vol. 36, no. 2, pp. 433-462, 2006. [http://dx.doi.org/10.2143/AST.36.2.2017929] |
| [9] | Z.M. Landsman, U.E. Makov, and T. Shushi, "Tail conditional expectations for generalized skew elliptical distributions", SSRN http://papers.ssrn.com/sol3/papers.cfm?abstract_id=2298265, Technical report., 2013. |
| [10] | J.B. McDonald, and Y.J. Xu, "A generalization of the beta distribution with applications", J. Econom., vol. 66, no. 1, pp. 133-152, 1995. [http://dx.doi.org/10.1016/0304-4076(94)01612-4] |




